嵌入式系統的細粒度多處理器實時搶占式調度算法
李 揚 王春明
1(江蘇商貿職業學院電子與信息學院 江蘇 南通 226011) 2(南通大學計算機科學與技術學院 江蘇 南通 226019)
0 引 言
如今AMD與Intel等處理器廠商已經發布8個核心以上的CPU,未來CPU的核心數量更可能達到百級,由此增加了多處理器、多任務調度問題的難度[1]。傳統的研究大多集中于單處理器,而針對單處理器的諸多研究成功無法擴展至多處理器系統[2]。為了充分利用多核心處理器的計算能力,任務調度算法需要支持任務之間的并行化[3-4],此外,對于多線程的任務,更可能發生同一任務的不同線程在多個處理器核心上并發執行的情況,因此,細粒度的任務調度算法成為一個亟待解決的問題[5]。
實時調度研究中有兩個基本問題:(1) 調度算法需為任務或線程分配合適的優先級,且滿足系統的截止期約束;(2) 為調度算法提供可調度性分析,證明算法滿足系統的截止期約束[6-7]。以往的研究大多從單線程多任務、多處理器的實時調度方面解決上述兩個問題。近期,出現多個考慮多線程多任務的多處理器調度研究,其中可調度性分析的研究為主要目標,但針對此場景的調度算法優化研究相對較少[8-10]。
單線程任務中,作業是基本的調度單位,該場景的實時調度算法根據優先級變化的時間點主要分為三類[11]:(1) 任務級固定優先級算法;(2) 作業級固定優先級算法;(3) 動態優先級算法。如果將線程作為調度單位,則為調度問題增加了一個維度,從而提升了問題的復雜度。
文獻[12]提出了最優優先級分配算法(OPA),該研究證明了OPA是任務級固定優先級分配問題的最優算法,本文期望將OPA算法擴展至線程級調度場景,但由此帶來兩個問題:線程級依賴關系與線程級調度算法的可調度性分析。本文首先采用任務分解方法[13]為各線程分配偏移時間與截止期;然后,基于干擾的線程級分析證明本文擴展調度算法與OPA算法兼容,從而證明本文線程級調度算法也是最優調度算法;最終,設計了完整的線程級調度算法。
1 系統模型
1.1 有向無環圖(DAG)任務
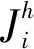
(a) DAG任務
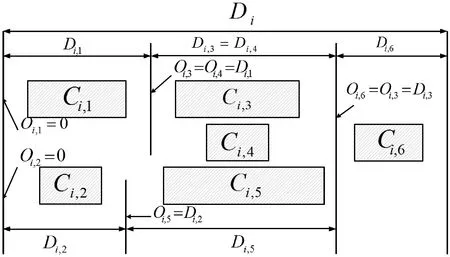
(b) 任務分解圖1 任務示意圖
1.2 任務分解
可將一個DAG任務分解為獨立、有序的子任務集合,線程之間具有依賴關系與執行出口,為DAG任務的各線程分配對應的偏移與截止期。
將任務τ分解產生的線程集合設為τdecom,τdecom中線程的數量設為n。對于任務τi,定義任務的主線程為θi,1,τi中其他各線程θi,p表示為(Ti,p,Ci,p,Di,p,Oi,p),其中Ti,p是最小間隔(等于Ti),Ci,p與Di,p分別表示最壞情況的運行時間及其截止期,Oi,p為對應的偏移(從Oi,1=0開始)。
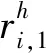
1.3 CPU平臺與調度算法
假設多核CPU由m個相同的處理器組成,調度策略為全局任務-線程級固定優先級調度,每個線程θi,p可以動態地在處理器之間遷移,且為所有線程分配靜態的優先級Pi,p。將優先級高于Pi,p的線程集合設為hp(θi,p)。
2 可調度性分析
DAG任務分解為線程級之后,各線程即設置了偏移與截止期,無需考慮線程間的依賴關系。基于干擾的可調度性分析兼容OPA,所以本文采用該方案[15]。
2.1 基于干擾的可調度性分析
線程級干擾可如下定義:
干擾Ik,q(a,b):如果θk,q為ready狀態,但[a,b)中更高優先級的線程正在運行,此時的時隙總和定義為干擾Ik,q(a,b)。
干擾I(k,q)→(k,q)(a,b):[a,b)中θi,p正在運行,且θk,q為ready狀態,此時的時隙總和定義為干擾I(k,q)→(k,q)(a,b)。
Ik,q(a,b)與I(k,q)→(k,q)(a,b)之間的關系是可調度性分析的重要基礎,Ik,q(a,b)與I(k,q)→(k,q)(a,b)之間的關系可推導為[16]:
(1)
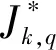
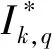
(2)
文獻[15-16]定義了以下可調度性判定條件:
引理1 當且僅當所有線程θk,q滿足以下條件,則m個相同處理器組成的多處理器平臺中集合τdecom是可調度的:
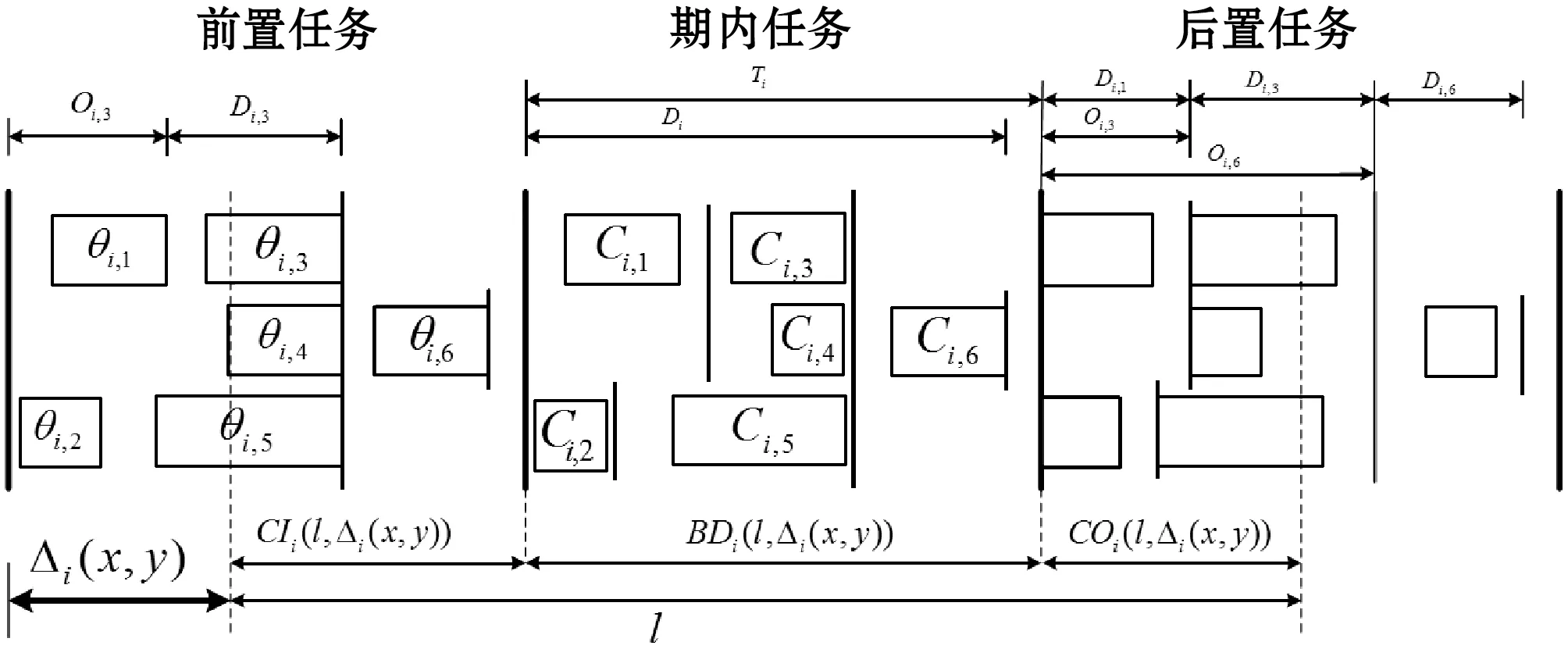
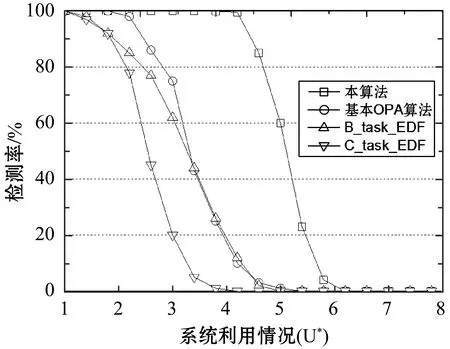
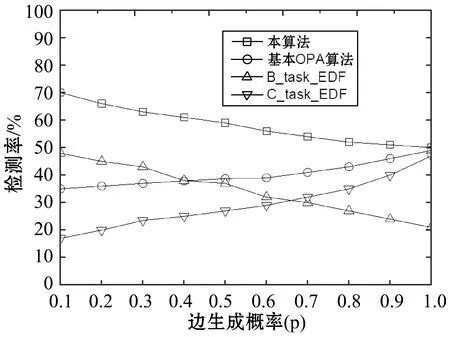
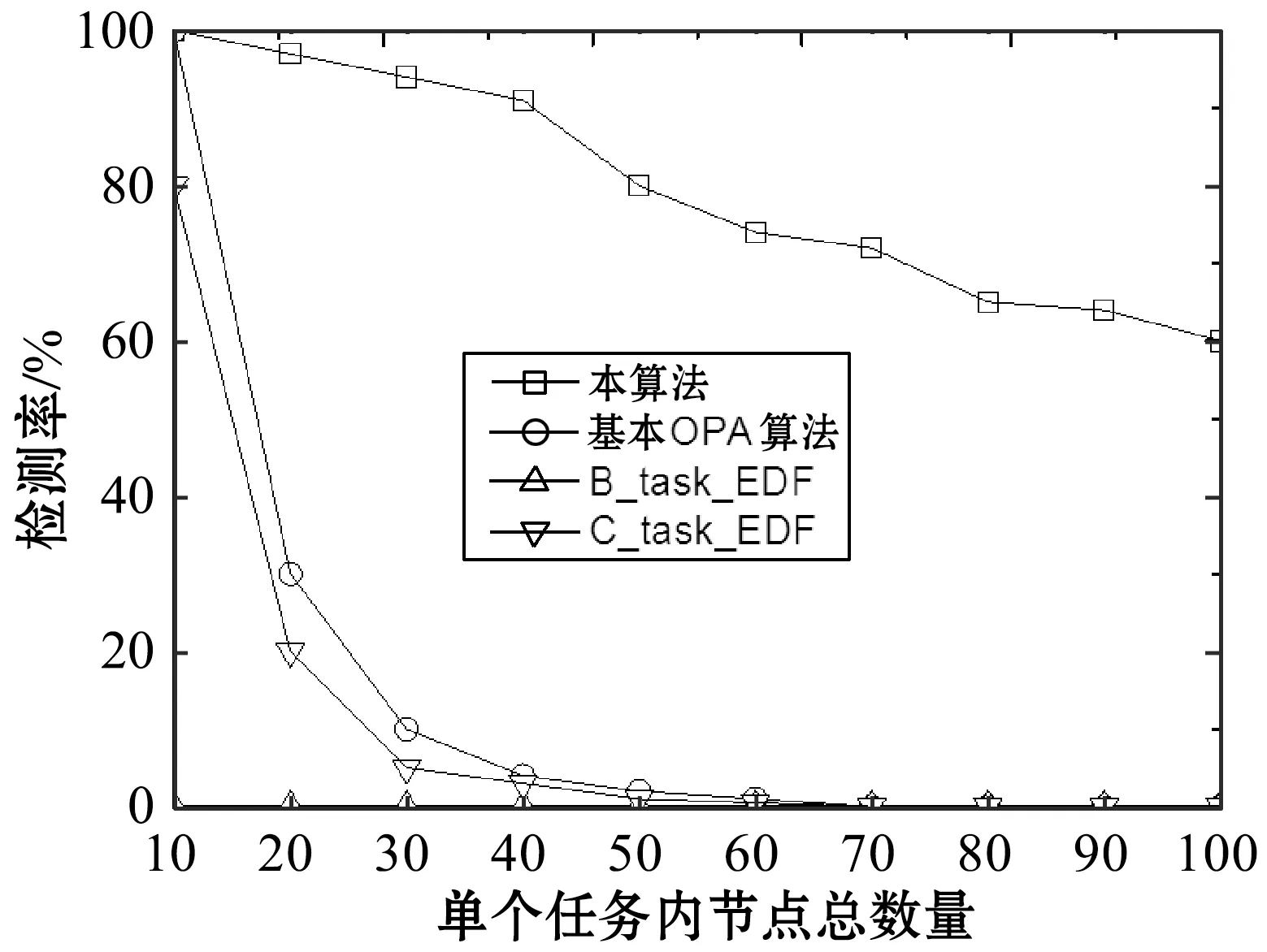
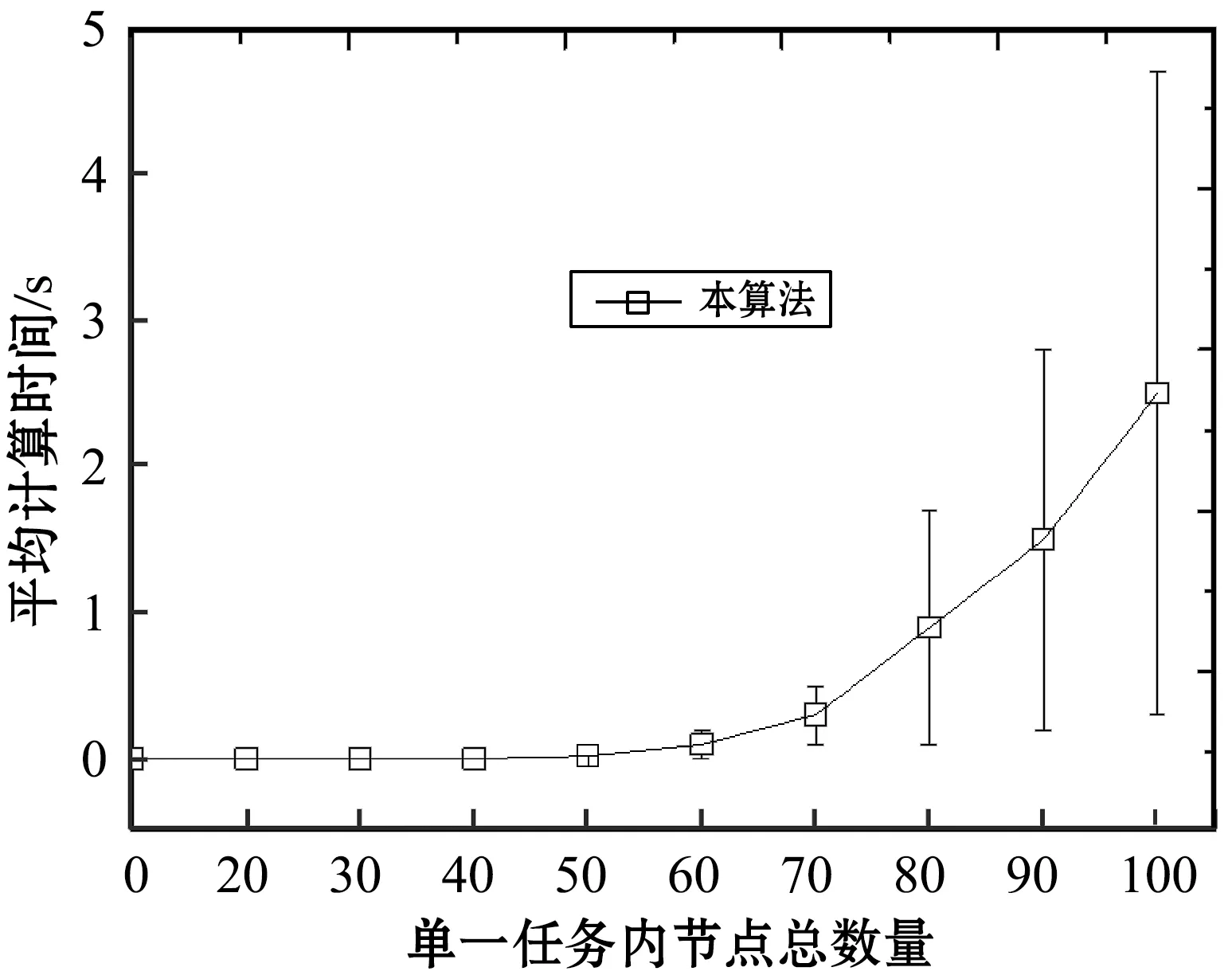
(3) 文獻[17]對引理1擴展,獲得了以下線程級判定條件: 引理2如果τdecom是可調度的,則τ也是可調度的。 首先需要確保各線程的截止期早于任務的截止期(引理1),然后需要計算其他線程對目標線程θk,q的干擾(式(3))。 考慮兩個場景計算最大工作負載:i≠k與i=k,原因在于i=k表示兩個干擾線程屬于同一個任務,說明τi中作業釋放的偏移已經自動給定。 2.2.1i≠k情況的負載最大化 為了簡化描述,對于時間段(x,y],如果作業的啟動時間在x之前,截止期在(x,y]內,則簡稱為前置作業;如果作業的啟動時間與截止期均在(x,y]內,則簡稱為期內作業;如果作業的啟動時間在(x,y]內,截止期在y之后,則簡稱為后置作業。 假設τi的作業為周期地啟動,定義Δi(x,y)為(x,y] 中前置任務啟動時間點與x的差值,如圖2所示。 圖2 τi中所有線程的最大工作負載 對于一個給定的Δi(x,y),如果(x,y]時長為l,可將(x,y]時間段分為前置時段CIi(l,Δi(x,y)),期內時段BDi(l,Δi(x,y))以及后置時段COi(l,Δi(x,y)),三種時段可表示為: CIi(l,Δi(x,y))=min(Ti-Δi(x,y),l) (4) (5) COi(l,Δi(x,y))=l-CIi(l,Δi(x,y))-BDi(l,Δi(x,y)) (6) 對于給定的Δi(x,y),(x,y]中每個線程的負載貢獻度(如圖2所示)可計算為: (7) 式中: 對于偶發任務:此時可簡單地檢查(x,y]中θi,p的運行量,則Δi(x,y)上界為Wi,p(l,Δi(x,y))。 考慮任務τi中Δi(x,y)的所有可能值,優先級高于θk,q的所有線程工作負載之和即為τi對線程θk,q的最大干擾的上界,表示為: (8) 2.2.2i=k情況的負載最大化 該情況下τk的作業被同一個任務干擾,因此可自動地決定τk中作業啟動的偏移時間。為了計算i=k情況的最大工作負載,本文僅需要考慮與線程θk,q重疊的部分執行窗口,使用式(7)可計算這些線程的負載貢獻量。因此,τk中優先級高于線程θk,q的其他所有線程最大負載計算為: Ck,q+1) (9) 基于式(8)和式(9)計算的干擾上界,為本文線程級調度算法設計了以下可調度性判定: 理論1對于m個相同的處理器平臺的線程級調度算法,如果每個線程θk,q滿足以下的不等式,則集合τdecom為可調度。 (10) 證明上文所述Wk(Dk,q)是θk,q運行窗口中優先級高于pk,q的最大運行量。當且僅當A優先級高于B時,A才對B產生干擾,式(3)左式的上界為式(10)的左式。根據引理1,可證明該理論。 問題描述為:給定一個分解線程的集合τdecom,為每個線程θi,q∈τdecom分配優先級Pi,p,因此根據基于工作負載的可調度性判定(理論1)認為分解集合為可調度的。 OPA算法通過優先級分配為各任務分配一個優先級,如果所有任務τi滿足以下兩個條件,則該可調度性判定為OPA兼容: 條件1:任務τi的可調度性對其他優先級的任務順序不敏感。 條件2:如果交換τk與τi之間的優先級使得τk的優先級提高,交換前后τk的可調度性不變。 算法1為本文改進的OPA調度算法,該算法從優先級最低的線程開始迭代地為所有線程分配優先級,其中τdecom為操作系統中待分配優先級的線程集。第k次迭代中,τdecom分為兩個不相交的子集:A(k)與R(k),其中: 1)A(k)表示第k步之前已分配優先級的線程子集; 2)R(k)表示剩余線程的子集。 理論1的可調度性判定是OPA兼容的,說明該判定滿足線程級可調度性的條件1與條件2,因此算法1的優先級分配過程正確,證明方法如下: 理論2理論1的可調度性判定兼容算法1。 證明根據本文的可調度性判定證明線程級調度算法滿足條件1與條件2: (1) 滿足條件1證明:式(10)的左式計算了每個任務對線程θk,q干擾的上界,任務的干擾上界計算為優先級高于θk,q的其他線程工作負載之和。而該計算過程不依賴相應的優先級順序。因此,滿足條件1。 (2) 滿足條件2證明:交換θk,q與θi,p優先級,θk,q的優先級提高。因為θk,q的優先級提高,所以hp(θk,q)交換后變得更小。因此,式(8)、式(9)的Wi(Dk,q)與Wk(Dk,q)交換之后變得更小,滿足條件2。 算法1線程級OPA調度算法 輸入:τdecom 輸出:調度狀態 1:k←0,A(1)←?,R(1)←τdecom 2:DO{ 3:k←k+1 4:IF(thread_level_sch(A(k),R(k))==FAILURE); 5:returnFALSE; //不可調度 6: }WHILE(R(k)!=NULL) 7:returnTRUE; //可調度 算法2thread_level_sch函數 輸入:A(k),R(k) 輸出:分配結果 1:FOREACHthreadθp,q∈R(k) { 2:IF(θp,q可調度,根據理論1,R(k)中其他線程的優先級均高于k)THEN{ 3: 為θp,q分配優先級k; 4:R(k+1)←R(k){θp,q}; 5:A(k+1)←A(k){θp,q}; 6:returnSUCCESS; 7: } 8: } 9:returnFAILURE; 上文考慮了線程靜態偏移與截止期的情況,本算法的決策目標為各線程的偏移、截止期與優先級三個目標,所以根據理論1的可調度性分析,并行任務系統是可調度的。本文動態截止期的線程級優先級分配策略的主要思想為:首先通過算法1分配優先級,如果算法1分配失敗,則調節一些線程的偏移與截止期,使得調節后某個線程可成功地分配優先級,如果找到該調節方法,則繼續使用算法1分配優先級;否則,認為調度失敗,如算法3所示。算法3中輸入為操作系統中待分配優先級的線程集,輸出為調度的狀態。 將線程結束時間與截止期之間的最小距離定義為線程θk,q的富余時間,表示為Sk,q。根據理論1的可調度性判定,Sk,q可近似為: (11) 線程間贈予富余時間的目標是為受贈線程分配一個優先級,使得受贈線程變為可調度,然而由此可能對其他可調度的線程產生邊際效應。考慮該問題,本文設計了以下三個子問題解決策略: (1) 受贈線程的決策策略:應當保證已分配優先級線程具有足夠的富余時間,所以決策策略為最小化總贈予時間的量。據此將所需贈予時間最少的線程作為受贈線程,時期變為可調度狀態,見算法4的第3行。 (2) 贈予線程的決策策略:確定受贈線程后,建立一個贈予線程候選集合(算法4第4行),屬同一個任務的候選線程已經分配了優先級,應當能夠贈予富余時間,且不影響所有線程的可調度性。為了避免破壞已分配優先級線程的可調度狀態,本文選擇候選集合中歸一化富余時間量最大的線程作為贈予線程(算法4第6行)。 (3) 贈予時間量的分配: 引理3如果線程θk,q的截止期Dk,q減小,則對θk,q最壞情況的干擾隨之單調減小。 證明式(8)、式(9)中,分別計算了τi與τk的最大執行量。式(7)中給定t,Wi,p(Di,p,t)與Wk,q(Dk,q,t)隨Dk,q下降而單調下降。式(8)中,因為需要調節Δi(x,y)使得Wi(Dk,q)最大化,所以Wk(Dk,q)不會隨Dk,q下降而提高,因此,可看出Wi(Dk,q)與Wk(Dk,q)隨Dk,q下降呈單調下降。由此證明引理3。 引理3說明如果贈予線程減小其截止期(將富余時間贈予受贈線程),贈予線程可能獲得其他的富余時間。因此,每個贈予步驟中將贈予時間設置較小,從而增加找到其他富余時間的概率(算法第7行),贈予完成后,每個贈予線程保持更新其富余時間量,以期找到其他的富余時間(算法11行)。 算法3動態截止期的線程級調度算法 輸入:τdecom 輸出:調度狀態 1:k←0,A(1)←?,R(1)←τdecom 2:DO{ 3:IF(thread_level_sch(A(k),R(k))==FAILURE) { 4:IF(deadline_change(A(k),R(k))==FAILURE) { 5:returnFALSE; 6: } 7: }WHILE(R(k)!=NULL); 8:returnTRUE 算法4deadline_change函數 輸入:A(k),R(k) //A(k)已調度的任務集,R(k)尚未調度的任務集 輸出:分配結果 1:F←R(k); 2:DO{ 5: 保存τs中所有線程的當前偏移與截止期; 10:returnSUCCESS; 12: } 13: 保存τs中所有線程的偏移與截止期; 14: }WHILE(F!=NULL) 15:returnFAILURE 為了簡化表達,定義以下術語:Ci表示τi(∑qCi,q)內所有線程最差情況的運行時間總和,Usys表示系統利用率,Li是τi最壞情況的執行時間,LUsys定義為任務τi∈τ中最大的Li/Di值。 采用文獻[18]的方法生成DAG任務,對于任務τi,其參數如下設置:節點數量ni均勻選擇于區間[1,Nmax]內,其中Nmax為單個任務的線程數量上限。每對節點之間邊隨機地生成,概率為p。根據Ci,p值所屬的三個范圍[1,5]、(6,10]、(11,40],分別為任務τi與每個線程分配一個類型(輕型、中等、重型),同時確定Ti(=Di)參數,因此Ci/Ti值分別在[0.1, 0.3],(0.3, 0.6]或(0.6, 1.0]隨機地選擇。 為了全面地測試本算法對并行DAG任務的性能,共設計了三種測試統計量:(1) 系統利用率;(2) 并行度;(3) 節點總數量。第一組實驗評估了系統對Usys的調度性能變化情況,結果如圖3所示。第二組實驗評估了算法對不同任務內并行度的調度性能變化情況,結果如圖4所示。第三組實驗評估了算法對τ中節點總數量的調度性能變化情況,結果如圖5、圖6所示。將本文算法與基本OPA算法[12]、B_task_EDF[19]以及C_task_EDF[20]三種算法進行橫向比較,評估本算法的性能。 圖3 不同Usys的調度性能變化情況 圖4 不同任務內并行度的調度性能變化情況 圖5 對τ中節點總數量的調度性能變化情況 圖6 本調度算法的計算時間與任務內節點總數量的關系 5.1.1 第一組實驗的任務集生成方法 步驟1:隨機地將任務逐個加入任務集中; 將U*從1增加至8,步長設為0.4,因此實驗的任務集數量為18 000。 5.1.2 第二組實驗的任務集生成方法 設置m=8、Nmax=10、p為變量因子,生成1 000個任務集,步驟如下: 步驟1:使用上述參數生成m個任務的任務集; 步驟2:如果任務集的Usys大于m,則忽略該任務集并返回步驟1; 步驟3:采用此時的任務集進行實驗,然后向該任務集添加一個任務,并返回步驟2直至生成1 000個任務集。 對于節點間的邊,如果p=0,則沒有邊(不存在父線程),此時任務內的并行度為最大;如果p=1,每個節點均與其他節點連接,說明一個任務內同時僅一個線程運行;隨著p值增加,每個DAG任務τi內邊的數量增加,由此導致關鍵的執行路徑Li變長,然后LUsys增加。 為了針對不同的任務內并行度進行仿真,在10個不同的p值下,進行仿真實驗,p值從0.1增加至1,步長為0.1,共有10 000個仿真。 5.1.3 第三組實驗的任務集生成方法 第三組實驗采用第一組實驗的參數設置,將任務逐個加入任務集直至τ中節點數量達到給定的節點總數量,任務的節點數量范圍為[1,給定的總節點數量-τ中節點數量]。將節點總數量從10增加至100,p=0.5,U*=m/2。每個數據點包含1 000個仿真,共有10 000個仿真。 從圖3中可看出,U*從1到5.8,本算法的檢測率遠超過其他三個算法。將本算法與OPA基本算法相比,可看出本文細粒度的調度算法(線程為調度單位)明顯提高了調度算法的性能,同時本算法優于兩個EDF的增強算法,可看出本算法中采用線程級調度、動態線程截止期等設計具有顯著的效果。 圖4所示為檢測率與p值的關系,p值增加引起每個DAG任務的邊數量增加,從而使得節點間依賴的關系度升高。從圖中可看出,線程級優先級分配算法在p值較小時具有較好的性能,而當p值為1時,本算法與基本OPA算法、C_task_EDF性能接近,此時一個DAG任務中所有節點均被連接,任務均為單線程任務。B_task_EDF的檢測率隨著p值的增加而降低,主要原因是該方法的調度性判定LUsys是否小于閾值m/(2m-1),隨著p值的增加,LUsys值升高,導致可調度性下降。 為了測試本算法對不同數量線程的性能,將線程數量設為因變量,統計系統檢測率的變化情況。圖5中可看出,節點數量較多時,本算法優于其他三個算法。節點數量越多,本算法調節線程截止期的機會越多,因此可調度性越高。 圖6是本算法計算時間與任務內節點數量的關系,可看出節點數量越高,算法的計算時間越高。雖然對于100個線程的任務,本算法的計算時間約為2.2 s,但是本算法將實時系統的檢測率提高到約60%。 現有實時系統調度算法將任務作為調度單位,嚴重限制了多線程任務的調度性能,并且已有的算法大多對一些經典的調度算法進行可調度性分析,以期通過優化可調度性判定條件提高算法的可調度性。然而受限于原調度算法的性能限制,通過收緊可調度性判定條件所獲得的性能提升往往較為有限。本文提出了一種細粒度的線程級多處理器實時調度算法,并給出了詳細的可調度性分析,仿真實驗結果表明,本算法對于多線程任務的實時系統具有較好的性能,對高線程數量的任務具有明顯地優勢。2.2 基于工作負載的可調度性分析
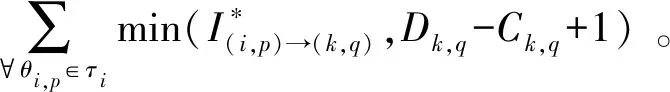
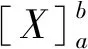
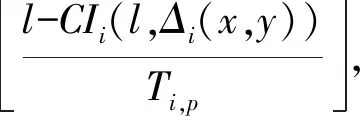
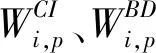
3 線程級最優優先級分配算法
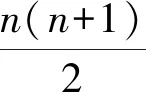
4 動態截止期的線程級調度算法
4.1 算法設計
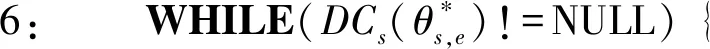
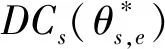
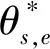
4.2 計算復雜度分析
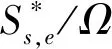
5 仿真實驗與結果分析
5.1 仿真環境
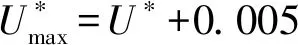
5.2 實驗結果與分析
6 結 語

