基于以SURF改進AKAZE的圖像匹配算法

趙柏山，鄭麗娟，陳 瑜

（1.沈陽工業大學信息科學與工程學院，沈陽110870；2.中國石油長慶油田分公司第四采油廠，銀川750006）

1 引 言

圖像匹配是指通過一定的匹配算法在兩幅或多幅圖像之間識別同名點的過程，主要可分為基于圖像灰度信息與基于圖像特征信息匹配兩類。其中，基于特征的圖像匹配技術，以其具有魯棒性高、計算量小的優勢取得快速的發展[1]。D. G. Lowe 于2004 年提出了尺度不變特征匹配算法（SIFT）[2]，該算法對圖像的旋轉、尺度變化等都是魯棒不變的，缺點是實時性差。H. Bay 等人于2006 年提出了加速魯棒特征算法（SURF）[3]，它依賴于圖像的高斯尺度空間分析，同時基于Hessian 矩陣[4]的行列式進行特征點檢測，利用積分圖像、Haar 小波響應提高檢測速度，采用Haar 小波變換增加魯棒性。SURF 特征不受旋轉和尺度的影響。與SIFT 相比，SURF 的主要優點是計算成本低，但是在目前各種匹配算法當中，其匹配速度比利用二進制描述符進行匹配的速度慢[5]。Alcantarilla 等人于2012 年提出了利用非線性擴散濾波和非線性尺度空間的KAZE 特征[6]。KAZE 特征對旋轉、尺度、有限仿射變換具有不變性，不足之處是計算成本高。Alcantarilla 等人于2013 年提出了加速的KAZE（AKAZE）算法[7]，該算法也是基于非線性擴散濾波的，但其使用FED 數學框架，從而動態地加快了非線性尺度空間的計算速度, 并且利用改進的局部差分二進制（M-LDB）[8]描述符，使其速度較KAZE 有很大提高，盡管如此，仍提高得不夠理想。故此提出一種改進方法，選擇將SURF 特征點檢測與AKAZE 特征點描述相結合，并利用漢明距離對圖像進行粗匹配，利用RANSAC 算法[9]剔除誤匹配點，使得算法在匹配速度及一些變換圖像的魯棒性方面[10-11]有進一步的提高。

2 AKAZE算法原理

2.1 特征點檢測

AKAZE 算法以各向異性的非線性濾波來構造尺度空間，非線性擴散濾波通常采用偏微分方程進行求解。經典非線性擴散方程如下：

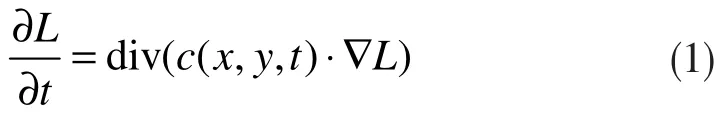
式中，div 和? 分別為散度與梯度，L 為圖像的亮度,c(x,y,t)為傳導函數。時間t 是尺度參數，數值越大表示圖像形式越簡單。

1) 構建非線性尺度空間

AKAZE 算法構建非線性尺度空間策略與經典SIFT 算法類似，其組數為o，每組的層數為S。通過以下公式將組數索引和層數索引映射到對應的尺度σ（像素）上[12]：

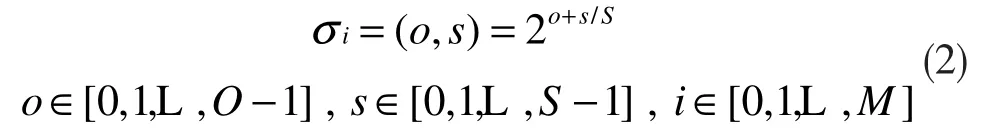
式中：M 是濾波圖像的總數。由于非線性擴散濾波作用于時間序列上，需將以像素為單位的尺度參數σi映射到以時間為單位的尺度參數ti,公式如下：

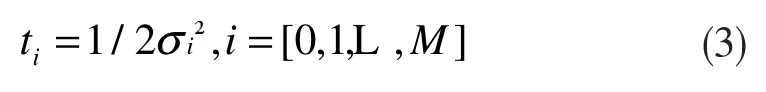
接著利用FED 算法求解式(1)，即可得到非線性尺度圖像，其式如下：

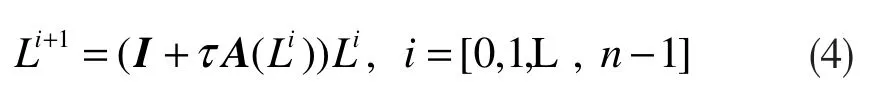
式中，I 為單位矩陣，A(Li)為圖像Li的傳導矩陣,τ 為時間步長，n 為顯式擴散步數。

2) 定位特征點

尋找不同尺度歸一化后Hessian 矩陣的行列式的局部極大值點，把采樣點的響應值與同尺度的8個鄰域點及相鄰尺度的2×9 個鄰域點比較判斷是否為最大值，然后將二維二次函數擬合到3×3 像素鄰域內Hessian 響應的行列式上，得到亞像素級精度的關鍵點的二維位置，如下式：

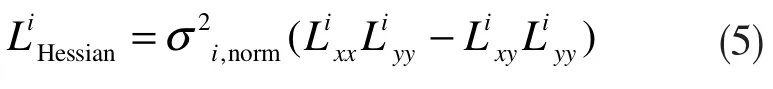
式中，σi，norm=σi/2σi，為對應圖像組中歸一化尺度因子，Lxx和Lyy分別為二階橫向和縱向微分，Lxy為二階交叉微分。

3) 判斷特征點主方向

與SURF 算法相似，在梯度圖像上以特征點為中心，在半徑為6σ 范圍內，取特征點鄰域的一階微分值Lx和Ly并對其進行高斯加權，接著用π/3 的扇形繞原點旋轉并計算該扇形向量和，主方向即為扇形向量和中的最長矢量方向。

2.2 特征點描述與匹配

二進制描述符（如BRIEF、ORB 和BRISK）最近得到了廣泛的應用，因為它們可以實現高效的計算和匹配。然而，這些二進制描述符利用過度簡化的信息，即用于二進制測試的圖像塊內的像素子集的原始強度，因此辨別能力不高。AKAZE 算法利用一種局部差分二進制描述符（M-LDB）,該描述符遵循和BRIEF 相同的原理，但在區域平均值之間使用二進制測試而不是單個像素，以獲得額外的魯棒性。

以任意給出的某圖像為例，LDB 將圖像分成n×n 個相等大小的網格單元并從每個網格單元中提取平均強度和一階梯度，如圖1(a)所示，用于計算直立的描述符；而M-LDB 描述符根據特征點主方向，將LDB 所劃分的網格單元做相應旋轉使其旋轉到主方向上，如圖1(b)所示，然后計算每個網格的平均強度和梯度，各公式如下：

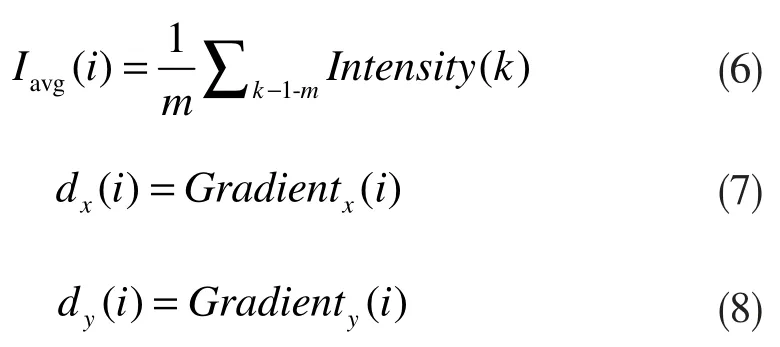
式中，m 為網格i 的總數，Iavg(i)為各網格單元的平均強度，dx(i)和dy(i)分別為網格i 區域的x 和y 方向的梯度。然后，LDB 分別比較成對網格單元之間的平均強度和梯度，根據比較結果，相應地設為0 或者1。其公式如下：

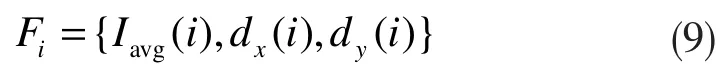
利用M-LDB 算子生成結果的是由0 和1 組成的二進制描述符，最終使用兩幅圖片特征點二進制描述符的漢明距離進行暴力匹配，生成匹配結果。

圖1 圍繞一個特征點的二進制測試網格劃分

3 改進的AKAZE算法

AKAZE 算法雖然利用了二進制描述符，但由于特征點檢測部分是用非線性濾波來構造尺度空間，因此匹配速度較慢。為提高匹配速度，現將SURF 特征點檢測與AKAZE 算法的M-LDB 描述符相結合，來實現圖像特征匹配。

3.1 基于Hessian矩陣的特征點檢測

利用Hessian 矩陣檢測特征點的方法是去計算圖像所有像素的Hessian 矩陣的行列式，極值點處就是圖像特征點所在的位置。

設圖像I 中有某點X=(x,y),則在該點處，尺度為σ 的Hessian 矩陣為：

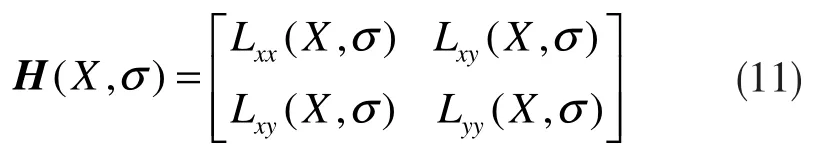
式中，Lxx=(X,σ)是高斯濾波后的圖像點X 在x 方向上的二階導數，Lyy=(X,σ)和Lxy=(X,σ)具有相似的含義。在構造Hessian 矩陣時應先進行高斯濾波，再計算二階導數。SURF 算法使用盒式濾波器來代替高斯函數，大大提高了運算速度。近似處理的效果如圖2 所示。

圖2 對高斯函數的近似處理

其中，圖2(a)、(b)、(c)分別為沿x 方向、y 方向、xy方向的高斯二階微分算子, 即Lxx模板、Lyy模板、Lxy模板；圖2(d)、(e)、(f)分別為盒式濾波器Dxx模板、Dyy模板、Dxy模板。在盒式濾波器中，白色部分的權值為1，灰色部分的權值為0，Dxx和Dyy中黑色部分的權值為-2，Dxy中黑色部分的權值為-1。Dxx，Dyy和Dxy可通過積分圖像求得。可用以下公式來近似計算Hessian 矩陣的行列式：

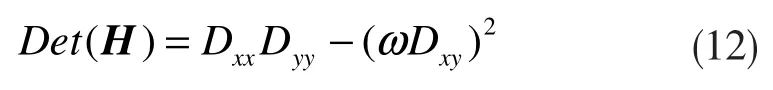
式中，ω 為權值，被用來平衡因子近似所帶來的偏差，其值為0.9。據此即可利用公式(12)得到每個像素點的Hessian 矩陣的行列式值的近似值。

為了使檢測到的特征點具有尺度不變性，通過改變盒式濾波器模板的大小，對圖像進行濾波，以產生多幅不同尺度的圖片；并通過公式(12)計算出不同尺度圖像下所有像素的Hessian 矩陣的行列式值。具體步驟為：首先取閾值，保留那些行列式值高的像素；然后將要檢測的像素與其鄰域的26 個像素點的行列式值做比較，去掉不是最大值的點；最后利用插值法來確定特征點的位置。

為獲得旋轉不變性，SURF 算法通過統計特征點鄰域內的Haar 小波特征確定其主方向。首先以特征點為中心，計算特征點鄰域（如半徑為6s 的圓，s為該點所在尺度）內的點在x,y 方向的Haar 小波響應[13]，用它即可以檢測出x 方向和y 方向上的梯度。Haar 小波邊長取4s，這樣每個扇形都得到了一個值。然后用60°扇形以一定間隔進行旋轉，將60°范圍內的響應相加以形成新的矢量，歷遍整個圓形區域，選擇最長矢量的方向為該特征點的主方向，如圖3 所示。

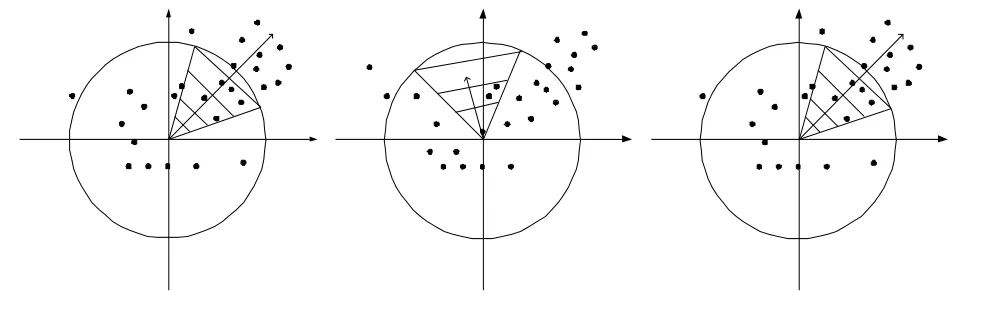
圖3 梯度坐標系內求方向

3.2 特征描述與匹配

在計算描述符之前，首先將不同尺度圖像以特征點為中心分成n×n 的小塊，并將圖像旋轉到主方向上，接著利用2.2 節所描述的AKAZE 特征描述方法來得到描述符，然后使用二進制描述符的漢明距離進行暴力匹配，得出匹配結果。在得出匹配結果之后，使用RANSAC 算法剔除誤匹配點，得到準確率較高的匹配圖像。

4 實驗與分析

4.1 實驗設計

使用牛津數據集中的不同模糊程度圖像（blurbikes）、不同程度的JPEG 壓縮圖像（JPEG ubc）、不同光照強度圖像（light.Leuven）、不同視角下的圖像（viewpoint.graf）,每種圖像變換的程度由從小到大的6 張圖片組成，通過第一張圖片與其后的5張圖片匹配得出匹配結果，把它們定義為第1～5組，對比它們的匹配時間與正確率。其中匹配時間是通過取30 次匹配時間的平均值得出的，匹配正確率是取30 次匹配正確率的平均值得出的。

實驗中，所用的電腦為Windows 10 系統，處理器為Intel（R）Core（TM）i5-3210M, 64 位操作系統，內存為4.00GB，并使用Visual Stdio 2015 進行實驗。

4.2 各變化條件下圖像

匹配結果及分析

不同模糊程度的圖像的匹配時間與匹配正確率的對比情況如表1、表2 所示。

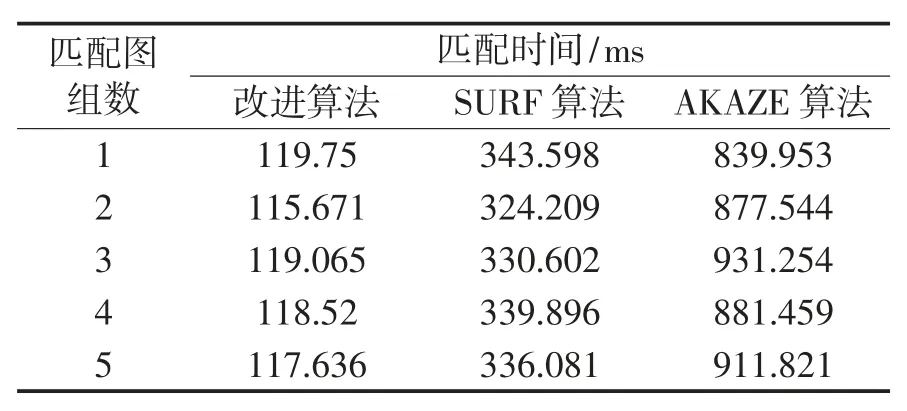
表1 不同模糊圖像匹配時間

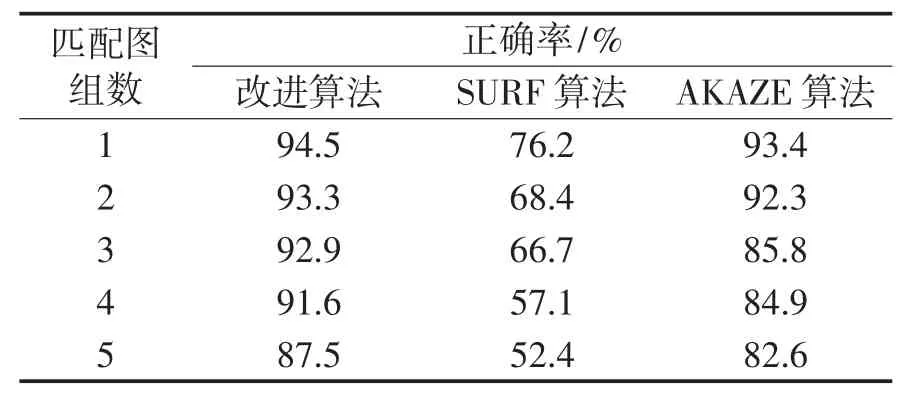
表2 不同模糊圖像匹配正確率

從表1，表2 可以看出，在不同程度的圖像模糊條件下，在匹配速度方面，本算法比SURF 的匹配速度平均快了近3 倍，比AKAZE 算法快了近8 倍；在匹配準確率方面，本文算法的正確率明顯比SURF算法高，比AKAZE 算法相比也有小幅度提高。

不同JPEG 壓縮圖像的匹配時間與匹配正確率對比情況如表3、表4 所示。

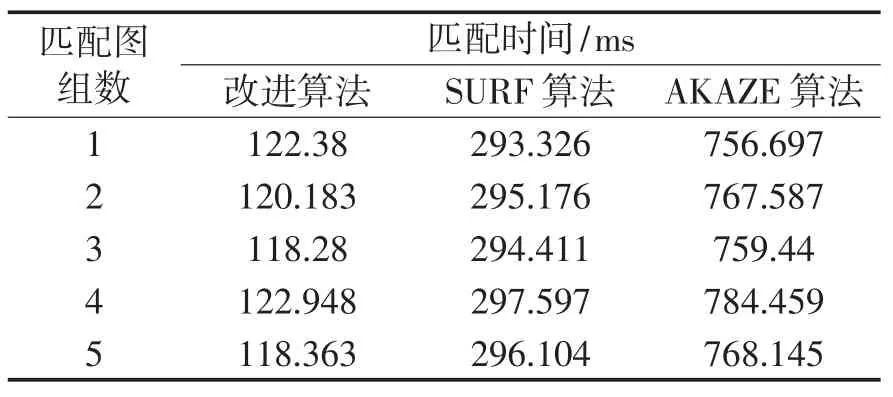
表3 不同JPEG壓縮圖像匹配時間

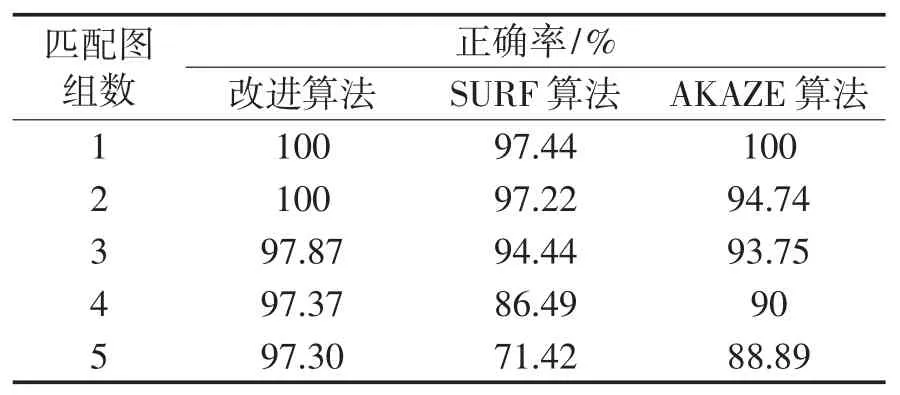
表4 不同JPEG壓縮圖像匹配正確率

從表3、表4 可以看出，在不同程度的圖像壓縮條件下，在匹配速度方面，本算法比SURF 的匹配速度平均快了2 倍多，比AKAZE 算法快了近7 倍；在匹配準確率方面，本算法比SURF 算和AKAZE 算法都要更高。

不同光照強度圖像的匹配時間與匹配正確率對比情況如表5、表6 所示。

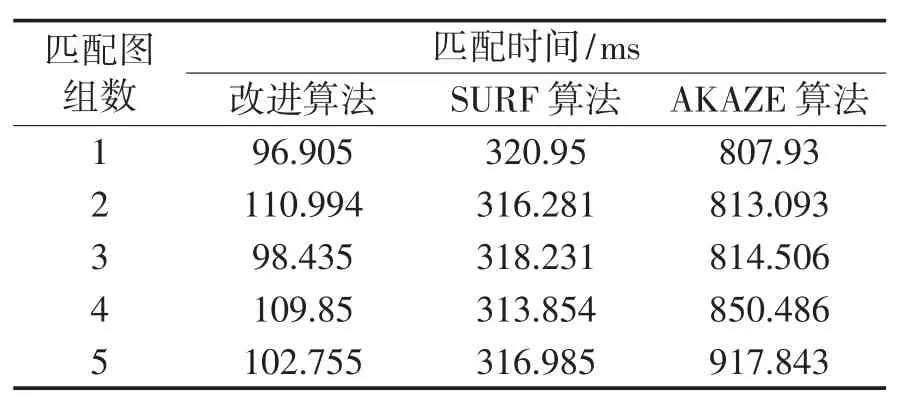
表5 不光照強度圖像匹配時間

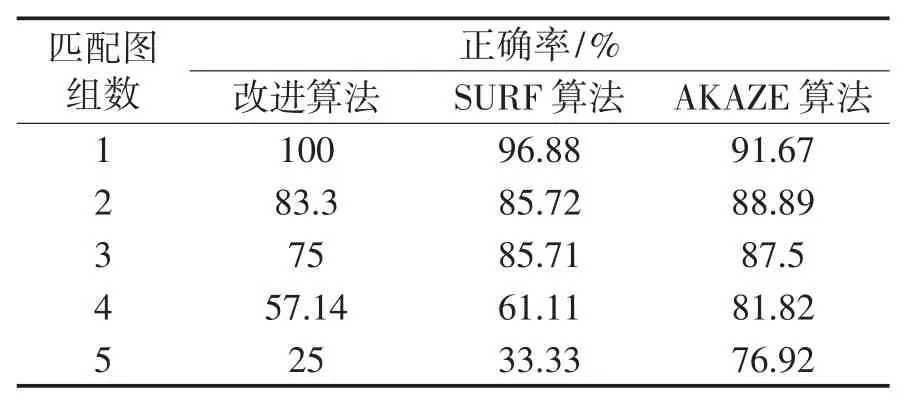
表6 不光照強度圖像匹配正確率

從表5、表6 可以看出，在不同光照強度的圖像匹配中，在匹配速度方面，本算法比SURF 的匹配速度平均快了近3 倍，比AKAZE 算法快了7 倍多；在匹配正確率方面，本算法在光照強度變化較小時，比SURF 算法和AKAZE 算法都高，但是在光照強度變化較大時，正確率還有待提高。

不同視角圖像的匹配時間與匹配正確率對比情況如表7、表8 所示。

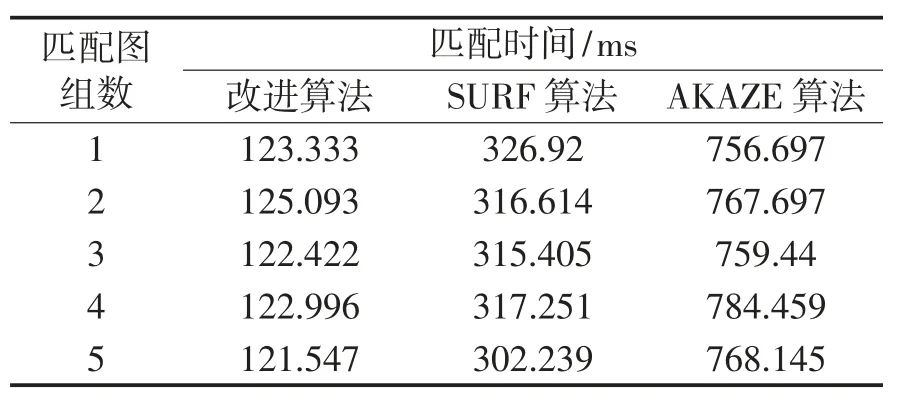
表7 不同視角圖像匹配時間

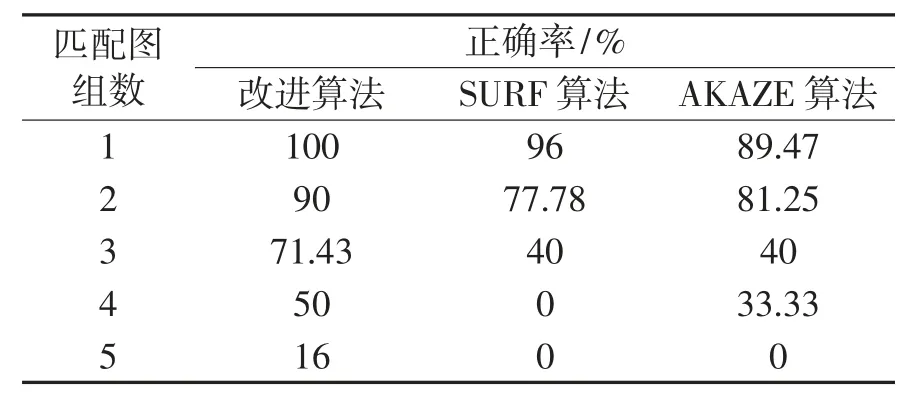
表8 不同視角圖像匹配正確率

從表7、表8 可以看出，在圖像的視角變化中，在匹配速度方面，本算法比SURF 的匹配速度平均快了2 倍多，比AKAZE 算法快了6 倍多；在匹配正確率方面，本文算法比SURF 算和AKAZE 算法都有明顯提高。

5 結束語

在提出的算法改進中，將SURF 算法與AKAZE算法相結合，在SURF 特征點檢測部分采用盒式濾波器以代替高斯函數進行濾波，提高了特征點檢測速度；而AKAZE 的特征點描述部分采用二進制描述符，匹配時使用漢明距離，速度也很快。由此可見，兩者結合后，算法的匹配速度比SURF 算法和AKAZE 算法提高很多。在不同模糊程度、不同JPEG壓縮、不同視角下的圖像匹配中，改進后的算法的匹配精度也比SURF 算法與AKAZE 算法更高。目前還存在著在不同光照強度下匹配精度較另外兩種算法為差的問題，對此如何解決，也將成為后續研究的重點。