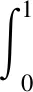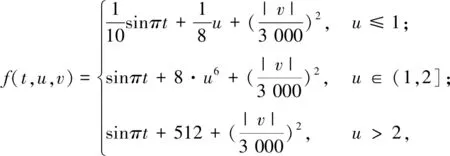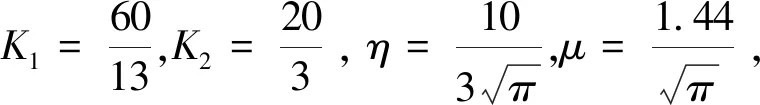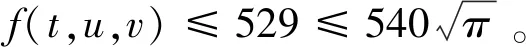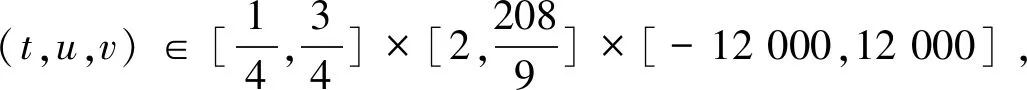帶有積分邊值條件的分?jǐn)?shù)階微分方程正解的存在性
,,
(山東科技大學(xué) 數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院,山東 青島 266590)
近年來,分?jǐn)?shù)階微分方程被廣泛應(yīng)用到各個(gè)研究領(lǐng)域,如流體力學(xué)、生物數(shù)學(xué)、控制和工程等。許多學(xué)者對(duì)分?jǐn)?shù)階微分方程解的存在性問題做了大量研究,并且已經(jīng)獲得了很多成果[1-17]。其中,不少文獻(xiàn)研究帶有積分邊界條件的分?jǐn)?shù)階微分方程正解的存在性[1-4,7-8,12-17]。
文獻(xiàn)[1]研究了一類具有積分邊界條件的分?jǐn)?shù)階微分方程邊值問題正解的存在性,通過利用Guo-Krasnoselskii不動(dòng)點(diǎn)定理得到了該問題至少有一個(gè)正解存在。文獻(xiàn)[2]研究了具有非局部項(xiàng)的奇異非線性共軛型分?jǐn)?shù)階微分方程正解的存在性,通過建立極大值原理、構(gòu)造上下解并運(yùn)用Schauder不動(dòng)點(diǎn)定理得到了至少有一個(gè)正解存在的充分條件。文獻(xiàn)[3]利用單調(diào)迭代方法及與格林函數(shù)有關(guān)的不等式獲得了非線性分?jǐn)?shù)階邊值問題有兩個(gè)非平凡解的存在性,而文獻(xiàn)[2-3]的邊界條件里都含有Riemann-Stieltjes積分。文獻(xiàn)[4]和[7]中,作者運(yùn)用Leggett-Williams 不動(dòng)點(diǎn)定理得到了Caputo型分?jǐn)?shù)階微分方程多個(gè)正解的存在性,且文獻(xiàn)[7]運(yùn)用Guo-Krasnoselskii不動(dòng)點(diǎn)定理及上下解方法獲得了該問題正解的唯一性和存在性。文獻(xiàn)[8]中,作者運(yùn)用上下解方法及Leray-Schauder度理論獲得了分?jǐn)?shù)階微分方程的積分邊值問題至少有三個(gè)正解的存在性。
從上面的文獻(xiàn)分析可以看出,研究帶有積分邊界條件的分?jǐn)?shù)階微分方程的相關(guān)成果已經(jīng)有很多。但是,這些工作均建立在非線性項(xiàng)中不顯含導(dǎo)數(shù)項(xiàng)的前提下。而本研究方程的非線性項(xiàng)中顯含一階導(dǎo)數(shù)項(xiàng),這是與以上所有文獻(xiàn)的不同之處。以上文獻(xiàn)處理帶有積分邊界條件的分?jǐn)?shù)階微分方程所使用的方法不適用于處理非線性項(xiàng)中顯含一階導(dǎo)數(shù)項(xiàng),而本文給出了該問題的處理方法。此外,給出的非線性項(xiàng)條件比文獻(xiàn)[4,7]中的更弱,是對(duì)現(xiàn)有文獻(xiàn)的一個(gè)推廣,也更具有普遍性。
本文研究如下分?jǐn)?shù)階微分方程邊值問題解的存在性:
(0.1)
u(0)=u(1)=0;
(0.2)
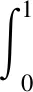
(0.3)
其中f:[0,1]×R+×R→R+,α1>β1>0,γ1>δ1>0,g,h∈C([0,1],R+), 導(dǎo)數(shù)。運(yùn)用推廣的 Leggett-Williams 不動(dòng)點(diǎn)定理,得到了邊值問題(0.1)~(0.3)至少存在三正解u1(t),u2(t),u3(t),最后給出數(shù)值例子來驗(yàn)證給出結(jié)果的正確性和有效性。
1 預(yù)備知識(shí)
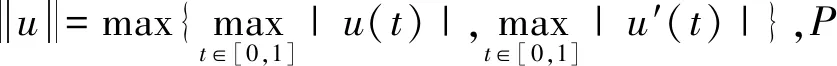
定義1.1設(shè)γ:P→[0,∞)是P上的一個(gè)非負(fù)連續(xù)泛函,若對(duì)所有x,y∈P,0≤t≤1,有γ(tx+(1-t)y)≥tγ(x)+(1-t)γ(y),則稱γ為P上的一個(gè)非負(fù)連續(xù)凹泛函。
定義1.2設(shè)α:P→[0,∞)是P上的一個(gè)非負(fù)連續(xù)泛函,若對(duì)所有x,y∈P,0≤t≤1,有α(tx+(1-t)y)≤tα(x)+(1-t)α(y),則稱α為P上的一個(gè)非負(fù)連續(xù)凸泛函。
設(shè)α,β:P→[0,∞)是兩個(gè)非負(fù)連續(xù)凸泛函,對(duì)給定正常數(shù)r,L,M,以及u∈P,有
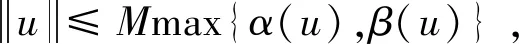
(1.1)
Ω={u∈P|α(u) (1.2) 顯然Ω是P上的非空有界子集。 定義1.3[9]給定常數(shù)r>a>0,L>0,α,β:P→[0,∞)滿足(2.1),(2.2),γ是P上的一個(gè)非負(fù)連續(xù)凹泛函,定義如下有界凸集: P(α,r;β,L)={u∈P|α(u) P(α,r;β,L;γ,a)={u∈P|α(u) 引理1.1[11]微分方程 u″(t)+y(t)=0,0 u(0)=u(1)=0, 且G(t,s)有如下性質(zhì): 1)G(t,s)≤G(s,s),0≤t≤1; 本文始終假設(shè)如下條件成立: (A0)κ=κ1κ4-κ2κ3>0,κ1≥0,κ4≥0,其中 引理1.2[4]微分方程 引理1.3[4]令 則有: 由引理1.1和1.2易得如下結(jié)果。 引理1.4微分方程(0.1)~(0.3)對(duì)應(yīng)的線性方程 u(0)=u(1)=0, 本節(jié)將運(yùn)用推廣的 Leggett-Williams 不動(dòng)點(diǎn)定理來得到問題(0.1)~(0.3)的解。 則問題(0.1)~(0.3)至少有三個(gè)正解u1,u2,u3,滿足 因此 對(duì)于 結(jié)合引理1.1,引理1.3及(A3),有 因此(2.1)式滿足定理1.1中的條件(iii)。 考慮如下形式的邊值問題: (3.1) u(0)=u(1)=0, (3.2) (3.3) 其中,q=3.5,α1=γ1=2,β1=δ1=1,h(t)=t3,g(t)=t2, 經(jīng)驗(yàn)證: (H1)~(H3) 滿足定理2.1的所有條件。因此問題(3.1)~(3.3)至少存在三個(gè)正解。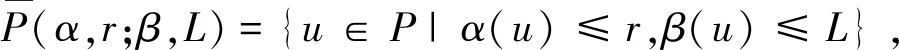
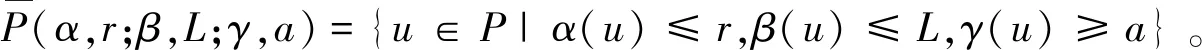
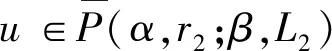
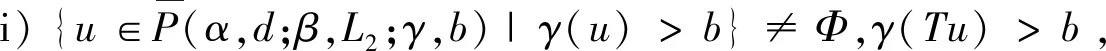
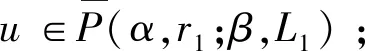
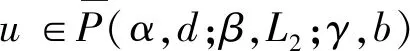
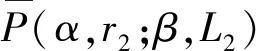
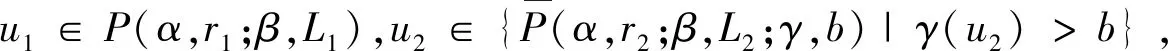
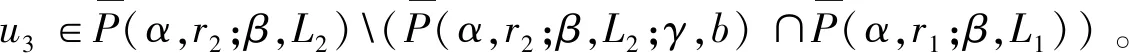
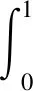
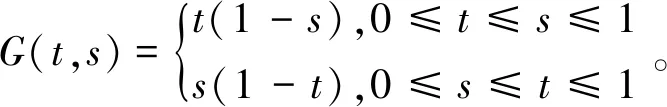
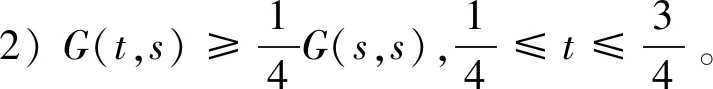
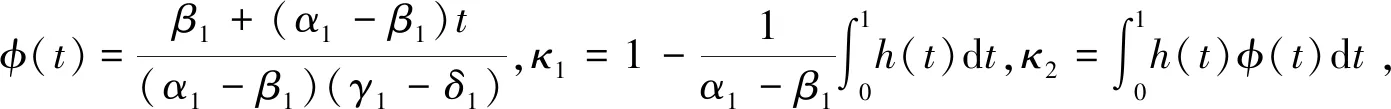
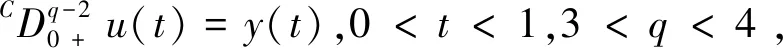
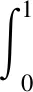
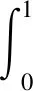
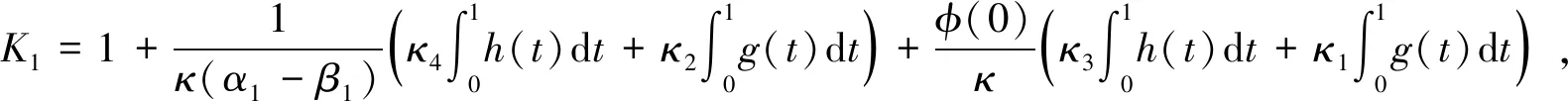
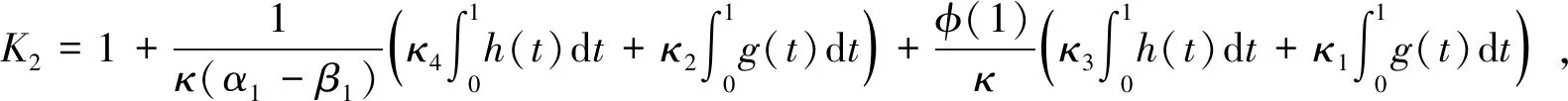
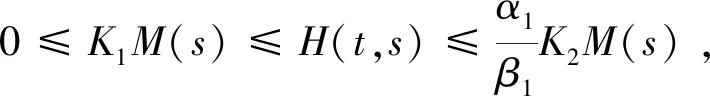
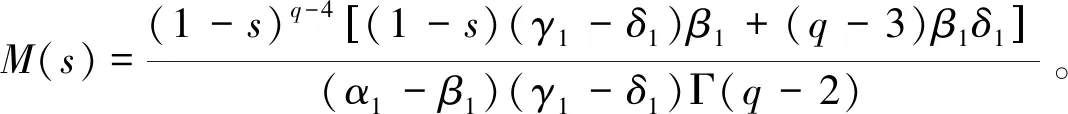
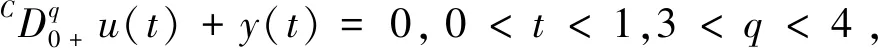
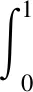
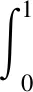
2 主要結(jié)果
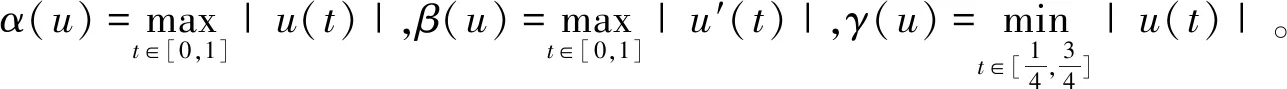
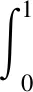
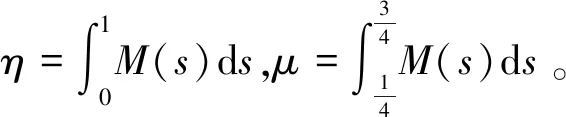
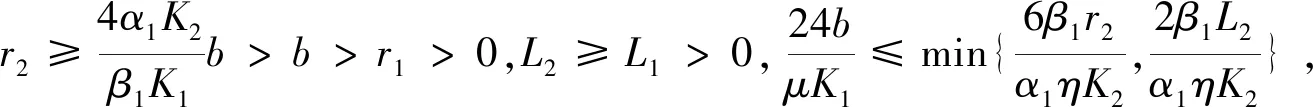
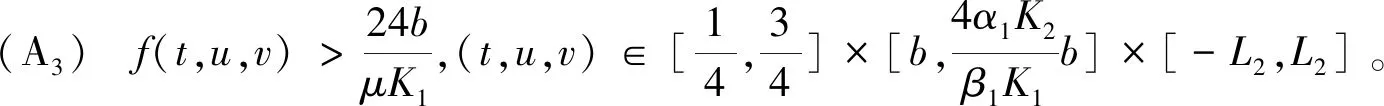

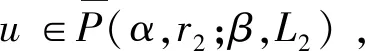
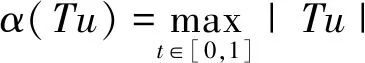
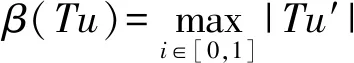
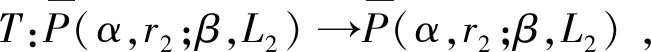
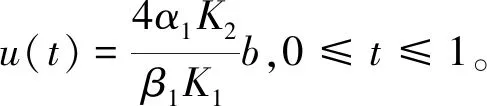
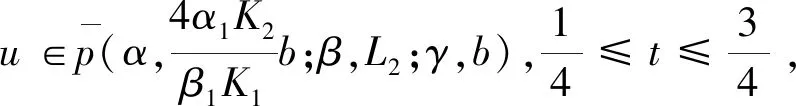
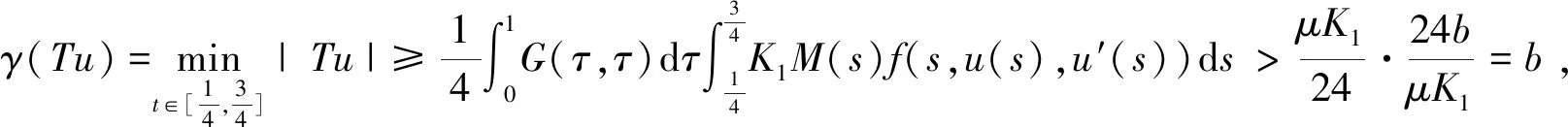
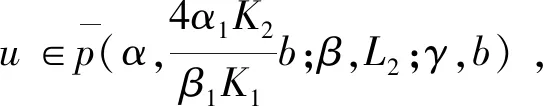
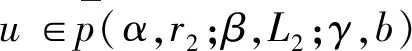
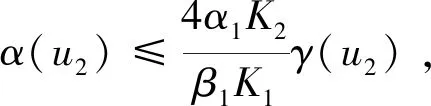
3 例子