基于改進不等時距灰色模型的老齡飛機結構腐蝕預測

, ,

(中國民航大學，天津 300300)

隨著民用航空產業的快速發展，中國飛機機隊規模的不斷擴大，老齡飛機所占比例也逐漸增加，老齡化現象隨之凸顯。據統計[1]，當飛機進入老齡期后，機體的維修成本每年將增加約5%；但是，由于老齡飛機的折舊或租賃費已基本付清，所以,老齡飛機和新型飛機的運營費用相差不大，有時甚至更低。同時，鑒于1988年阿羅哈事件等數起航空安全事故，世界各國當局對飛機設計制造、維修工程管理和運行安全都高度重視。我國民航局也在CCAR121R5文件中新增了附件J《航空器持續適航與安全改進》，明確了老齡飛機的維修方案以及適航性要求。因此，對老齡飛機的維護、運營以及持續適航性要求已成為航空公司及相關院校的主要研究內容。

飛機進入老齡階段后，會發生電氣電路系統老化、機械磨損加重、零部件性能衰退等問題，其中腐蝕問題隨著飛機使用年限的增加日益明顯。而這些腐蝕損傷累計到一定程度，不但會給民用機的維修帶來巨大壓力，同時還會加重飛機的運營成本。因此，研究服役老齡飛機的腐蝕發展規律，預測結構的腐蝕壽命具有十分重要的工程意義。老齡飛機的腐蝕損傷問題多是由涂層、飛行載荷、地面停放環境等多種因素聯合作用導致的。而這些因素在實際的老齡飛機服役過程中很難得到定量化的結果；此外老齡飛機服役多年后，其結構件的腐蝕數據多是散亂的，可用數據量小且存在缺失現象。因此，本工作基于老齡飛機在運行中的結構件腐蝕信息，采用改進的不等時距GM(1，1)模型，對老齡飛機結構件的腐蝕進行預測。以期在數據存在少量缺失的前提下，對老齡飛機的結構件腐蝕進行精準預測。

1 老齡飛機結構件的腐蝕現狀

1.1 老齡飛機的定義

參考波音設計服務目標(Design Service Objective DSO)的概念，確定老齡飛機如下：對于窄體客機，老齡飛機的門檻值為運營時間累計達到15 a或75%設計服役目標(DSO)(先到為準)；對于寬體客機，老齡飛機的門檻值為運營時間累計達到20 a或75%設計服役目標(DSO)(先到為準)[2-3]。設計服役目標又稱經濟設計目標壽命，可以是飛行小時、飛行循環(FC)和日歷時間中的一個或他們的組合。各機型 DSO 飛行循環參見下表。

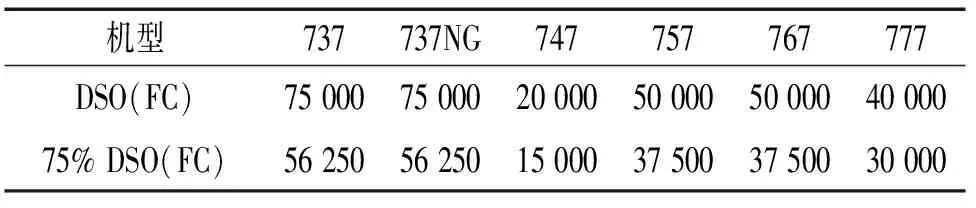
表1 各機型DSO飛行循環Tab. 1 DSO flight cycles of different airplanes

民用機的壽命對飛機的安全使用有很大的制約作用，對于老齡飛機，腐蝕的嚴重程度更決定了飛機的使用壽命。因此，對典型結構件的腐蝕情況進行預測是至關重要的[4]。目前，關于飛機的腐蝕研究主要有如下兩種方式：一種是根據腐蝕數據，用數學理論建立腐蝕隨時間的發展模型；另一種是根據腐蝕機理，選擇腐蝕參數，建立腐蝕隨時間的變化模型。

由于飛機在運營過程中的多種腐蝕影響因素數據很難定量測量，因此本工作采用灰色模型，挖掘數據的內在規律以對飛機結構件的腐蝕進行預測。

1.2 民用機的腐蝕現狀

現役老齡飛機普遍使用高強度鋁合金材料，飛機長期服役于腐蝕環境中，在熱交變載荷作用下,加上表面防護層的意外損傷,機體普遍發生腐蝕。金屬結構的腐蝕類型主要有均勻腐蝕、縫隙腐蝕、點蝕、晶間腐蝕、應力腐蝕開裂和腐蝕疲勞等。表2為在役飛機結構件的腐蝕等級劃分及維修方案[5]，表中D表示飛機結構原厚度。

表2 在役飛機結構件的腐蝕等級劃分及維修方案Tab. 2 Corrosion state classification and maintenance plan for structural components of aircraft in service

根據某公司提供的廣州基地腐蝕檢修數據，發現民用機的腐蝕損傷多為電化學腐蝕，其腐蝕形貌主要為點蝕和剝蝕。點蝕形狀多為半球或橢球形[6-7]，且蝕坑深度對飛機結構件的服役性能有較大影響，因此本工作對點蝕較為嚴重的飛機后貨艙地板梁的最大蝕坑深度進行預測，進而預測其服役壽命。分析數據源自廣州基地某型飛機449份維修工卡數據。

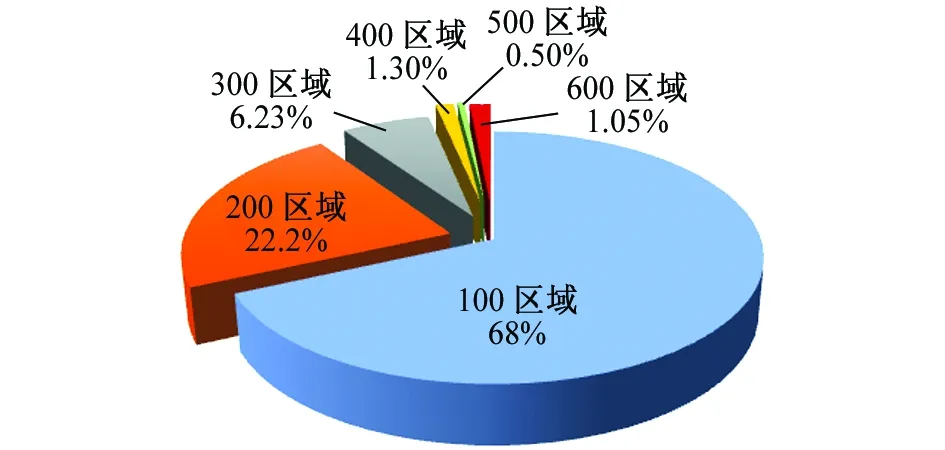
圖1 民用機的腐蝕區域分布Fig. 1 The regional distribution of civil aircraft corrosion

由圖1可見：民用機在100區域即飛機下半部分發生的腐蝕最為嚴重，這主要是因為機身下半部既為飛機的主要承力部位，又承載著大量的飛機系統及部件。各種異類金屬相互接觸，少量潤滑油、燃油等電解質溶液的存在促使結構部件發生腐蝕。其次，民用機的機身下半部多為貨艙、廚房等設施，存在較多具有腐蝕性的物質，這加劇了腐蝕。此外，機身下半部還易受到飛石、鳥撞等偶然損傷使之防護層遭到破壞，基體金屬暴露更會促進腐蝕，破壞結構件的強度，降低結構件的性能。

2 灰色模型

灰色預測GM(1，1)模型是由鄧聚龍教授推出的，已廣泛應用于社會經濟的各個領域。其理論研究對象是“小樣本”、“貧信息”的不確定性系統，該模型通過對部分已知信息的開發實現對問題的確切描述[8]。其中，處理不等時間間隔數據的方法分為兩類:一是通過對原始數據進行預處理，使不等時間間隔數據等間隔化(常用插值法)，但此類方法主觀性高，且插值的優劣可能會改變數據原有的變化規律，因此在實際應用中存在較大誤差。二是直接對預測模型進行改進，在對原始數列的處理中加入時間乘子，根據新的累加數列重新構造背景值，采用該方法能取得較好的預測結果。

2.1 不等間距GM(1,1)模型的基本理論

設原始序列為：

x(0)={x(0)(t1),x(0)(t2),x(0)(t3)……x(0)(tn)}

(1)

其中，tk為序列所在x(0)(tk)所處的時刻。Δtk=|tk-tk-1|,k=1,2,3,…n。當Δtk不為常數時，稱為不等間距序列。

累加生成序列：

(2)

x(1)(t1)=x(0)(t1)

(3)

構造背景值：

(4)

微分方程：

(5)

其中，a，b為灰色模型的特征參數，a為發展系數，b為灰作用量，利用最小二乘法得出：

(6)

其中，

(7)

Y=[(x(0)(t2)Δt2，x(0)(t3)Δt3，…，x(0)(tn)Δtn]

(8)

得出時間響應數列：

(9)

還原得到原始數列：

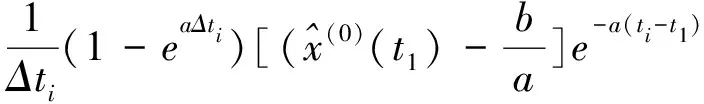
(10)

當k>n時，可以預測出序列的第n+1以及以后的序列。

2.2 改進不等間距GM(1,1)模型

本工作通過改進不等灰色模型的初始值，背景值及引入權重因子，提高了模型預測精度。

2.2.1 優化初始值

灰色模型的初始值對模型的精度有著至關重要的影響，通常采用原始序列的第一個點作為初始值，但實際的最優曲線并不一定經過歷史數據的某一點，同時新數據的產生往往對未來的發展有更加重要的影響，因此本工作用最新的三個數據點的均值來代表初始值。

(11)

2.2.2 背景值優化

背景值是直接影響灰色模型預測精度的關鍵因素，通常采用梯度公式進行近似計算。但該方法容易產生較大誤差，因此本工作采用公式(12)進行計算[9];

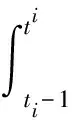
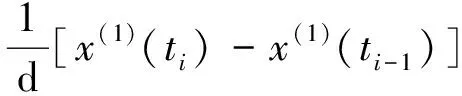
(12)

又因

(13)

兩邊取對數得：

(14)

代入上式整理得：

(15)

2.2.3 加權權重參數求解

數列中的各數據在灰色模型的預測中往往會有不同的價值；越新的數據對模型所占的權重越大，可靠度也越大。因此本文對不同時間點的值賦予一個權值，即

(16)

其中，w為權遞增因子，取值w=1.5。

而后根據灰色模型理論，利用最小二乘法得出參數估計值見式(6)～(10)

(17)

3 老齡飛機腐蝕預測

在實際的維修工作中，由于飛機腐蝕區域比較分散，對于腐蝕數據的統計并不全面；與此同時老齡飛機使用年限較長數據存在丟失現象，因此本工作采用改進后的不等間距灰色模型進行腐蝕預測，降低對數據連續性的要求，更加符合實際的工程應用。

對廣州基地同型號，在相同服役環境中的民用機的后貨艙地板梁的腐蝕深度進行預測；其中源數據的時間間隔單位為C檢周期(C檢即飛機常規例行檢查，C檢時間間隔約為3200飛行小時)。

由于源腐蝕數據量大且分散，本工作對源數據進行預處理，對同一時期腐蝕區域內的最大蝕坑深度進行均值運算，見表3。

表3 后貨艙地板梁的腐蝕情況Tab. 3 Corrosion data of floor beam in rear cargo hold

依據改進不等間距灰色模型進行建模，得出改進UGM(1,1)模型如下:

參數值：

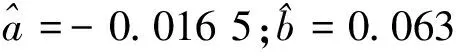
(18)

預測數列：

(19)

將預測結果與實際數據進行比對，如表4所示。

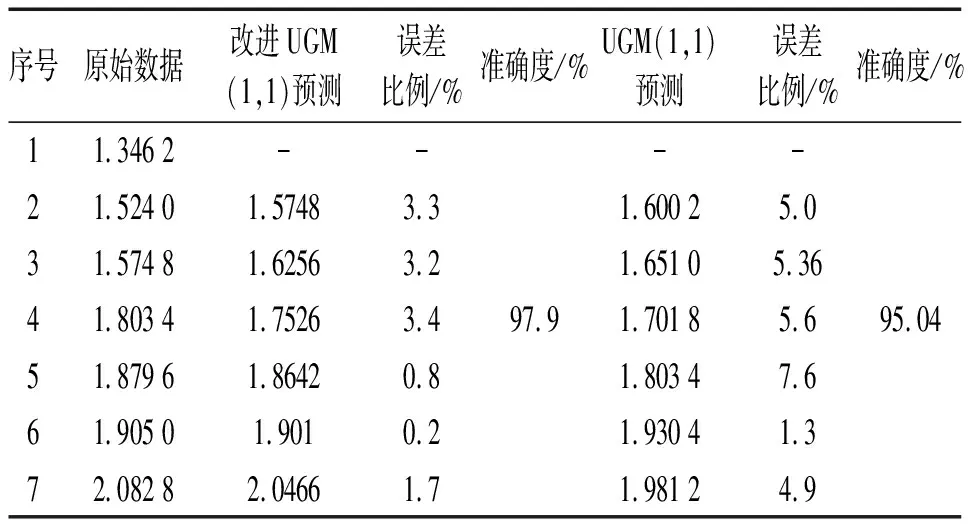
表4 模型改進前后的預測結果Tab. 4 Prediction results before and after the improvement of model

由表4可見：改進后的不等間距灰色模型預測結果的相對誤差小于改進前模型的。改進的背景值以及引入的權重因子能夠更好地反映數據的變化規律，得到更加精準的預測結果。因此，對于老齡飛機腐蝕深度的預測問題，可以使用改進的UGM(1，1)模型進行預測。

本工作采用的地板梁結構件的厚度D為22.75 mm，根據民用機腐蝕打磨深度不得超過0.1D的原則，約在定檢級別為23C時，腐蝕深度達到2.29 mm，接近腐蝕損傷容限上限，應該進行更換作業。根據改進模型的計算結果，可以對結構件的更換以及航材的儲備等進行一定的預先處理，減少機務的負擔及相應的維修成本。

4 結論

針對在役老齡飛機的腐蝕特點，以及腐蝕數據的特性，選用不等間距灰色模型進行預測。通過優化背景值，增加權重因子提高了的模型精度，使之達到約98%，即所建模型可用于腐蝕條件下在役飛機結構件的壽命預測。通過得到結構件的壽命年限，可以有效規避結構件發生失效，確保飛機的飛行安全；同時通過提前預知腐蝕結構件的壽命可有針對性地對其進行檢查，降低機務的工作負擔，對航材進行合理有效的儲備，降低人工費和材料儲存費。