基于云計算平臺實現電網短期負荷預測算法的研究

,,志遠,

(國網烏魯木齊供電公司,新疆 烏魯木齊 830011)

0 引 言

電力工業的根本目標是通過科學的規劃最大限度地提高發電和用電效率，提高電力系統運行的經濟性。而電力負荷預測一直是電力系統有效規劃和經濟運行的重要組成部分。

短期電網負荷預測是電力系統運行決策的關鍵，對電力系統的機組組合、減少發電備用、提高經濟調度、保持系統可靠性以及維護調度都有重要意義[1-2]。近年來，準確的短期電網負荷預測在電力市場管制中得到了更大的重視和面臨更大的挑戰。

短期電網負荷預測算法需要處理從一個小時到幾天的負載預測。由于短期負載具有極大的隨機性，因此短期電網負荷預測的復雜性對電力運營者是一個極大挑戰。在過去的幾十年里，人們提出了許多預測模型。這些預測模型可以分為傳統模型或基于機器學習的模型。前者包括時間序列預測器，如自回歸移動平均外生變量模型[3]。這些傳統模型是基于線性回歸模型，不能準確代表復雜負載的非線性特征[4]。不同的機器學習技術也被用于短期電網負荷預測，如人工神經網絡(artificial neural network,ANN)[5]、徑向基函數(radial basis function,RBF)[6]、模糊神經模型[7]和支持向量回歸[8]。

預測過程依賴于對某一國家或地區電力需求歷史數據的分析，還可以考慮許多其他因素，如天氣預報和商業計劃。因此，需要整個歷史數據來訓練預測模型，但是這樣的方法其缺點是，如果考慮到新的信息則所有參數都可能需要重新訓練。此外，這種龐大的數據量和預期的復雜預測過程導致需要大量的計算能力。研究人員試圖找到近似方法來最小化這一數據量，并將所需的計算能力降到最低。這些研究試圖盡量減少數據采樣量等。許多方法解決了這些回溯問題，其中一個采用了中的局部預測器[9-10]。

經濟約束在任何算法研究中都起著主要作用。云計算的出現解決了研究人員和開發人員面臨的許多經濟問題。在云計算技術之前，超級計算機是獲得巨大計算能力的唯一合適選擇，顯然這是一個非常昂貴的選擇。有許多計算系統可以提供巨大的計算能力，如分布式系統、網格計算、互聯網計算以及量子計算等，但云計算技術是最具性價比的選擇，獲得了廣泛的商業應用。為此，一些研究試圖借助云計算技術為短期負荷預測提供足夠的計算能力[11-13]。

1 基于支持向量回歸的短期負荷預測算法

一般來說，電力負荷由不同的消耗單元組成。各種因素都影響著電力負荷的變化，如天氣、重大事件、經濟因素和隨機因素。短期負荷預測可以被認為是一個多變量預測問題。它可以作為回歸問題的函數來求解。次日負荷為回歸模型的輸出，歷史負荷數據及其影響因素為回歸模型的輸入。歷史數據庫提供訓練數據。該回歸問題的最終目標是從歷史負荷數據及其影響因素中找到一個具有良好泛化能力的預測負荷映射函數。歷史負荷數據被分為兩個不同的數據集：一個是訓練數據集用來訓練回歸模型；另一個是測試數據集用來評估訓練后的回歸模型[14]。

基于統計學習理論提出的支持向量回歸(support vector regression,SVR)[15]已被研究作為一種有前景的電力負荷預測方法。其優勢主要來自于采用結構風險最小化原理，并作為經驗風險最小化原則的替代方案，它可以通過求解二次問題來獲得最優的全局解。

SVR的執行有兩個主要特征：二次規劃和核函數。二次規劃問題將用線性約束求解得到SVR的參數。核函數的靈活性使該技術能夠搜索寬范圍的解空間。SVR的主要目標是通過非線性映射將數據x映射到高維特征空間，并在該特征空間中執行線性回歸[16-17]：

f(x)=〈w,x〉+b

(1)

式中：<.，.>表示點積；w包含必須從數據中估計的系數；b是一個實常數。使用Vaunink的ε-不敏感損失函數[18]，將整體優化為

(2)

約束條件為

(3)

(4)

約束條件為

(5)

輸出是一個獨特的全局優化結果，其形式如下：

(6)

式中，Q(xi，x)是核函數。在SVR中采用核函數，所有必要的計算可以直接在輸入空間中計算。核函數存在各種各樣的內核，如線性、雙曲正切、高斯徑向基函數、多項式等[19]。在這里，使用常用的RBF內核：

Q(xi,x)=e-γ‖xi-x‖2

(7)

SVR的參數C、γ和ε在SVR的性能中起著至關重要的作用。因此，選擇這些參數的正確值可以最大限度地減少預測誤差。基于核的SVRs需要計算數據集中每個點之間的距離函數

(8)

基于SVR解決短期電網負荷預測問題可以歸納為以下步驟：

1)加載歷史數據并將其分為訓練集和驗證集；

2)準確確定SVR的參數；

3)使用定義的參數訓練SVR以獲得支持向量和相應的系數；

4) 利用式(6)得到預測的負載。

2 實驗驗證

為檢驗云計算平臺在電力負荷預測領域的影響，實驗旨在測試兩點：一是使用Azure ML實現負荷預測技術的準確性；二是測試執行時間的改進。

2.1 數據集

該數據集收集了從2016年1月至2017年12月的0.5 h電力負荷、2016年至2017年的日平均溫度以及2016年至2017年的假期信息。目標是預測2018年1月的每日最大負荷，并用2018年1月的負荷實際值驗證計算預測值。

2.2 實驗平臺

設計實驗的實現有兩個選擇：本地實現和基于云的實現。對于本地實現，可使用臺式計算機及使用MATLAB軟件實現所提出的算法。臺式計算機具有以下規格： Microsoft Windows 10，Intel Core i7 2.7 GHz，RAM 16 GB。 對于基于云的實現，則用Azure ML[20]。

2.3 性能指標

實驗考慮了兩個主要的性能指標：第1個也是最重要的一個是執行時間(TExecution)；第2個是預測準確性。所有實驗將使用4個度量來評估預測準確度：平均絕對百分比誤差(MAPE)、最大誤差幅度(MAX)、平均絕對誤差(MAE)和歸一化均方誤差(NMSE)。這些值由式(9)至式(13)定義：

(9)

MAX=max(|Ai-Pi|)

(10)

(11)

(12)

(13)

2.4 結果與討論

實驗包括了4種不同的實驗方案，用以比較和評估所提出的基于SVR算法的短期電網負荷模型在云計算平臺和單機計算平臺上的性能差異。

所有這些實驗方案的目標是使用訓練集訓練上面所述的預測模型，再使用這個預測模型來預測2018年1月的31天內的最大日負荷，并與實際負荷進行比較。所提出的各實驗方案的訓練數據有所不同，如表1所示。

表1 實驗方案的數據集

4種實驗方案的執行結果如表2、圖1和圖2所示。結果表明，使用云計算平臺的執行時間遠遠少于使用基于本地機器的單機計算平臺的執行時間。特別是在訓練數據相對較大的在實驗方案2中，云計算平臺與單機計算平臺的執行時間相比，時間執行的改進在10倍以上。值得指出的是，在云計算平臺上進行的第2次實驗時比第1次運行更快，例如，實驗方案2的第2次執行時間等于9 s，遠低于第1次的72 s。此外，從預測精度來看，兩者幾乎相同，在實驗方案4的情況下實現了最佳預測精度為2.04%。

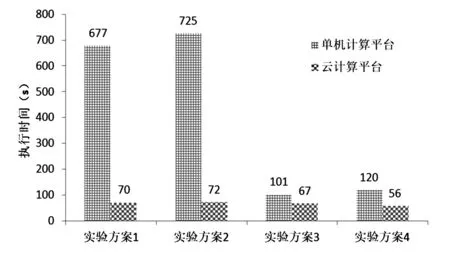
圖1 單機平臺和云平臺執行時間對比

3 結 論

前面提出了一種基于支持向量回歸預測(SVR)算法短期電網負荷模型，并通過實驗分別在云計算平臺和單機計算平臺上實現了該模型。在兩個平臺的對比實驗中，選擇執行時間和預測精度作為性能指標。對于所使用的實驗數據集，單機計算平臺和云計算平臺實現的算法預測精度是相同的；但是，在云計算平臺實現的算法執行時間顯著減小。一般來說，SVR并不推薦用于大型數據集，因為它的計算成本很高，而前面采用云計算平臺體現了較好的計算效率，因此所進行的實驗結果可為相關研究提供借鑒。

表2 實驗結果

圖2 各個實驗方案下預測值和實際值的偏差