周期為2q理想幾乎四進(jìn)制序列構(gòu)造研究
彭秀平,冀惠璞,鄭德亮,牛曉霞
(1.燕山大學(xué)信息科學(xué)與工程學(xué)院,河北 秦皇島 066004;2.河北省信息傳輸與信號處理重點實驗室,河北 秦皇島 066004)
1 引言
四進(jìn)制序列由于具有恒定的包絡(luò)特性和系統(tǒng)易于實現(xiàn)等特性,被廣泛應(yīng)用于雷達(dá)、聲納、導(dǎo)航、碼分多址(CDMA,code division multiple access)等實際通信系統(tǒng)中。在實際應(yīng)用中,為了實現(xiàn)同步、抗多徑干擾和防止載波泄露等需求,通常要求所采用的序列具有盡可能低的自相關(guān)函數(shù)旁瓣值和好的平衡性。自相關(guān)函數(shù)旁瓣值全為0的序列稱為最佳序列,而最佳二進(jìn)制序列僅存在長度為4的(1,1,1,?1)情況,最佳四進(jìn)制序列僅存在長度為2、4、8和16的情況,且平衡的最佳四進(jìn)制序列根本不存在[1]。為此,對理想四進(jìn)制序列和理想幾乎四進(jìn)制序列的研究受到了國內(nèi)外學(xué)者的廣泛關(guān)注,對于奇數(shù)長的理想四進(jìn)制序列,Schotten等[2-3]構(gòu)造了周期為(其中p為奇素數(shù),a為正整數(shù))的一類旁瓣值全為1的理想四進(jìn)制序列。隨后,Lüke等[4]利用改進(jìn)的Legendre序列構(gòu)造了理想奇周期四進(jìn)制序列。對于偶數(shù)長的理想四進(jìn)制序列,Tang等[5]證明了周期為偶數(shù)長的平衡四進(jìn)制序列的自相關(guān)函數(shù)旁瓣值最大模值至少為2的特性,并明確了此周期長平衡四進(jìn)制序列的理想情況為自相關(guān)函數(shù)旁瓣模值為小于等于2的情況。逆Gray映射將二進(jìn)制序列同四進(jìn)制序列建立了聯(lián)系,隨后這種方法被廣泛應(yīng)用于構(gòu)造具有理想自相關(guān)特性的平衡或幾乎平衡的四進(jìn)制序列,主要包括采用Sidelnikov[6]序列、理想自相關(guān)二進(jìn)制序列[7]、Legendre序列[8]等。此外,分圓類方法也被廣泛用于四進(jìn)制序列的構(gòu)造中,Edemskiy等[9]運用四階分圓與中國剩余定理結(jié)合的方法分別得到了2種旁瓣值為{-4,2,-2,0}和{-2±2i,±2i,-2}且周期為N=2q(q為奇素數(shù))的平衡四進(jìn)制序列,但是其旁瓣值的最大模值分別為4和8,不符合平衡理想四進(jìn)制序列的標(biāo)準(zhǔn),在此基礎(chǔ)上,Shen等[10]基于廣義分圓類思想,提出了2種新的可以得到周期為N=2q(q為奇素數(shù)),旁瓣值為{2,-2}的理想四進(jìn)制序列的構(gòu)造方法,但是此方法將四進(jìn)制序列0位置和q位置的元素值固定為1和–1,屬于四進(jìn)制序列元素的特殊情況。
為了進(jìn)一步擴(kuò)大理想四進(jìn)制序列的存在范圍,近些年,通過在序列中引入適當(dāng)個0元素的方式,有關(guān)理想幾乎四進(jìn)制序列的構(gòu)造方法被相繼提出。代表性成果有Tang等[11]通過引入一個0元素的方式,基于四階分圓的方法構(gòu)造得到一種周期為素數(shù)且N≡1(mod4),旁瓣值為-1的理想幾乎四進(jìn)制序列。彭秀平等[12]中通過引入4個0元素基于交織法對周期為N≡0(mod4)且旁瓣值為{0,-4}的幾乎四進(jìn)制序列的構(gòu)造方法進(jìn)行了研究。本文通過在四進(jìn)制序列中引入一個或2個0元素的方式,基于中國剩余定理和四階分圓類對周期為N=2q(q為奇素數(shù))的理想幾乎四進(jìn)制序列的構(gòu)造方法進(jìn)行研究,根據(jù)幾乎四進(jìn)制序列y的y(0)和y(q)這2個位置中含0個數(shù)不同提出相應(yīng)構(gòu)造方法,當(dāng)(y(0),y(q))=(0,0)時,得到2種旁瓣值為{0,-2}和{0,2,-2}的平衡理想幾乎四進(jìn)制序列,當(dāng)y(0)和y(q)中有一個位置為0時,得到2種旁瓣值為{0,2,-2}和{0,-2,-2i,2i} 的平衡理想幾乎四進(jìn)制序列。
2 基本概念
定義1[13]設(shè)周期為N的序列y=(y(0),y(1),???,y(N-1)),其中y(t)∈{1,-1,i,-i},i=-1,則稱序列y為四進(jìn)制序列,其自相關(guān)函數(shù)定義如式(1)所示。
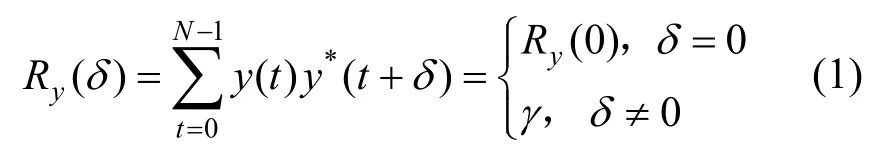
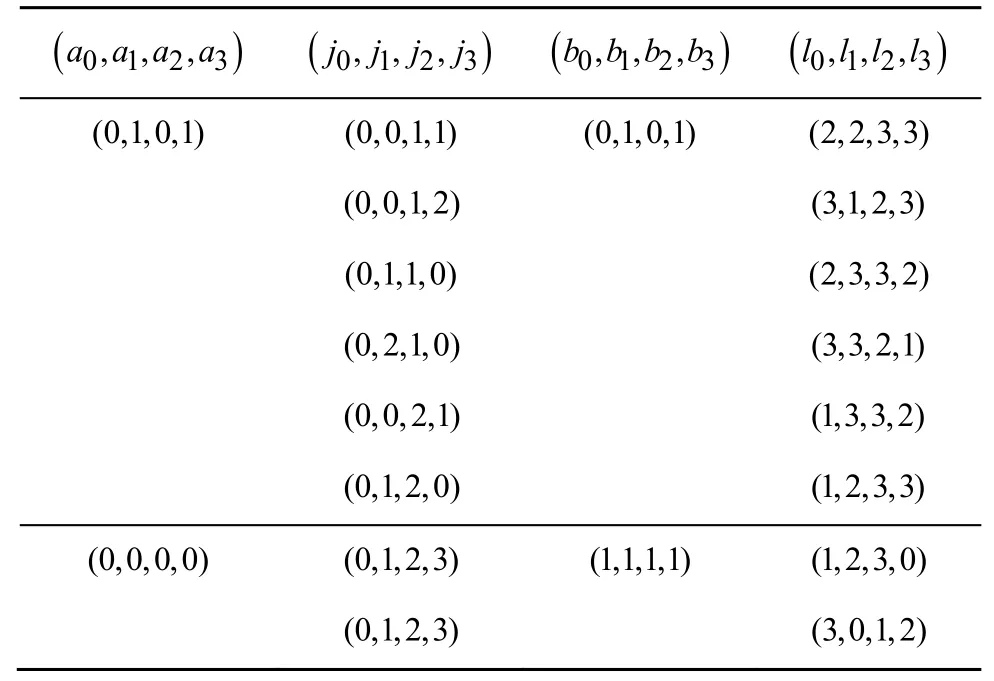
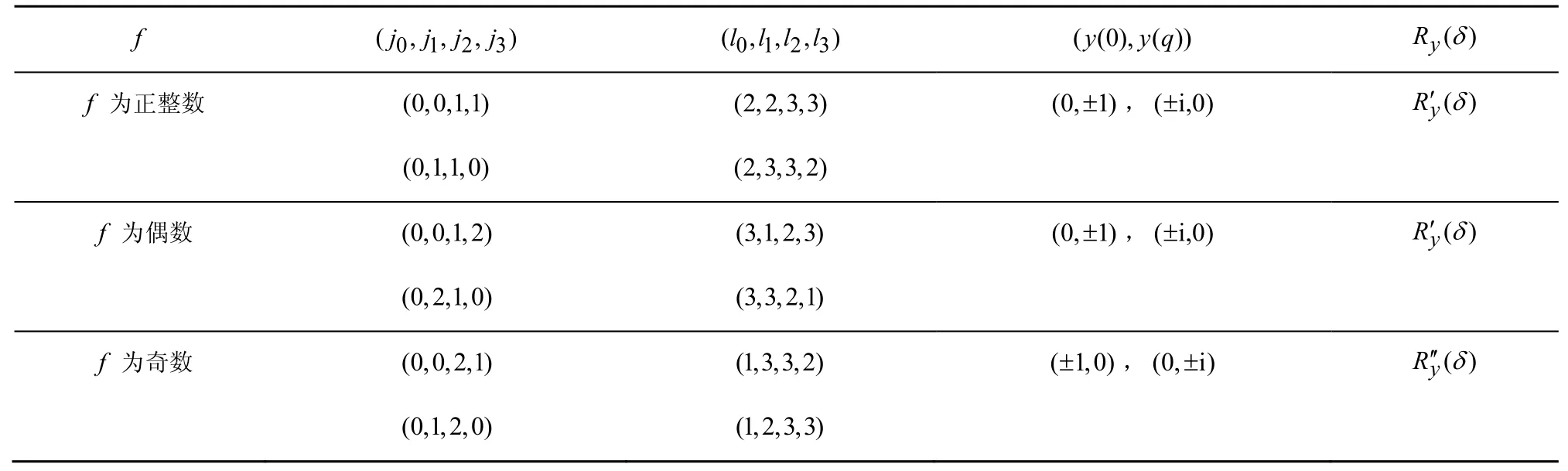
其中,0≤δ 引理1[5]設(shè)表示序列y的自相關(guān)函數(shù)的最大旁瓣模值,那么對于周期為N≡0(mod2)>2的平衡四進(jìn)制序列,一定滿足Rmax≥2。因此,若周期為N≡0(mod2)>2的平衡四進(jìn)制序列y的自相關(guān)函數(shù)滿足Rmax=2,則稱序列y為平衡理想四進(jìn)制序列。 本文基于此理論界,通過在四進(jìn)制序列的基礎(chǔ)上引入一個或2個0元素的方式,提出了幾種滿足此理論界,周期為N=2q的平衡理想幾乎四進(jìn)制序列的構(gòu)造方法。 定義2[13]設(shè)q=4f+1為奇素數(shù),θ是有限域GF(q)上的本原元,令 則稱Hi為GF(q)上的四階分圓類。令 其中,Hi+1代表集合{hi+1,hi∈Hi},“+”代表和模q,則(i,j)稱作基于GF(q)的四階分圓數(shù)。 引理2[13]設(shè)q=4f+1為奇素數(shù),其中f為正整數(shù)。q又可表示為q=4m2+n2,其中m、n均為正整數(shù)。根據(jù)f的奇偶性和n≡1(mod4)或n≡3(mod4)不同取值將四階分圓數(shù)進(jìn)行如下分類。 當(dāng)f為奇數(shù)時,Zq上的四階分圓數(shù)的關(guān)系如式(4)所示,Zq上的四階分圓類的5個基本分圓數(shù)如表1所示。 表1 當(dāng)f為奇數(shù)時,Zq的四階分圓數(shù)的5個基本分圓數(shù) 當(dāng)f為偶數(shù)時,Zq上的四階分圓數(shù)的關(guān)系如式(5)所示,Zq上的四階分圓類的5個基本分圓數(shù)如表2所示。 表2 當(dāng)f為偶數(shù)時,Zq上的四階分圓數(shù)的5個基本分圓數(shù) 引理3[14]根據(jù)中國剩余定理,Z2q?Z2×Zq存在如式(6)所示映射關(guān)系。 定義3周期為2q的幾乎四進(jìn)制序列y(t)定義如式(7)所示。 其中,y(0),y(q)∈{0,1,-1,i,-i},并且y(0),y(q)中至少有一個為0。 定義4設(shè)周期為N的幾乎四進(jìn)制序列y的元素集為Y={0,1,-1,i,-i},Y*=Y/{0},令當(dāng)滿足式(8)所示條件時,幾乎四進(jìn)制序列y稱為平衡序列。 定義5[10]設(shè)A和B是整數(shù)環(huán)Z2q上的2個子集,差函數(shù)dδ(A,B)定義為 其中,B+δ代表集合{b+δ:b∈B},“+”代表和模2q。 定理1設(shè)q=4f+1=4m2+n2為一奇素數(shù),其中f為正整數(shù),令(y(0),y(q))=(0,0),由式(7)定義的序列y(t)中各參數(shù)滿足表3所示集合時,構(gòu)造得到的幾乎四進(jìn)制序列均是理想平衡幾乎四進(jìn)制序列,且其相關(guān)函數(shù)值如式(11)所示。 表3 滿足定理1的序列y(t)的參數(shù)集合 證明以(a0,a1,a2,a3,)=(0,1,0,1),(j0,j1,j2,j3,)=(0,0,1,1),(b0,b1,b2,b3,)=(0,1,0,1),(l0,l1,l2,l3,)=(2,2,3,3)為例進(jìn)行證明,根據(jù)定義3可以得到 因為(y(0),y(q))=(0,0),所以由定義4可知,該構(gòu)造方法所得的幾乎四進(jìn)制序列y是平衡的。 令序列y的自相關(guān)函數(shù)Ry(δ)=Re(Ry(δ))+iIm(Ry(δ)),其中Re(Ry(δ))表示Ry(δ)的實部,Im(Ry(δ))表示Ry(δ)的虛部。由定義5、引理4和引理5可以計算得到式(13)和式(14)。 1)當(dāng)δ0=0,δ1=0時,顯然,Ry(0)=2q-2。 2)當(dāng)δ0=0,δ1≠0時,令δ1∈Hh,h∈{0,1,2,3},由引理2和引理6可知, a)若f為奇數(shù),則Ry(δ)=2[3(0,0)+(0,2)-(0,1)-(0,3)-2(1,0)](16) 當(dāng)n≡1(mod4)時,Ry(δ)=-2。 當(dāng)n≡3(mod4)時,Ry(δ)=-2。 b)若f為偶數(shù),則 Ry(δ)=2[3(0,2)+(0,0)-(0,1)-(0,3)-2(1,2)](17) 退役復(fù)學(xué)高職生有的在陸軍服役,有的在海軍服役,有的在空軍、武警等部隊服役;有的雖然屬于同一兵種,但服役崗位不同;有的是普通戰(zhàn)士,有的是特種兵。兵種和身份的不同,決定了他們在部隊的生活經(jīng)歷有很大差異。從調(diào)研結(jié)果看,特種兵比其他兵種更具有責(zé)任心和積極進(jìn)取的精神,更樂于無私奉獻(xiàn);在部隊擔(dān)任過領(lǐng)導(dǎo)職務(wù)或立過軍功的戰(zhàn)士,大多數(shù)都是黨員,復(fù)學(xué)后更容易成為班級的骨干或核心人物。 當(dāng)n≡1(mod4)時,Ry(δ)=-2。 當(dāng)n≡3(mod4)時,Ry(δ)=-2。 所以,Ry(δ)=-2。 3)當(dāng)δ0=1時,由于{0}∩{1}=0,因此 Ry(δ)=Re(Ry(δ))=0。 綜上所述,其相關(guān)函數(shù)值如式(11)所示,由此可知得到的幾乎四進(jìn)制序列為理想平衡幾乎四進(jìn)制序列。其他組合情況證明過程與上述證明過程類似,不再贅述。證畢。 例1設(shè)q=17=4×4+1=4×22+1,取θ=2,可以得到 根據(jù)定理1可以得到 且其相關(guān)函數(shù)值為 推論1當(dāng)q=4f+1=4m2+n2為一奇素數(shù),m為奇數(shù),n=1,且(y(0),y(q))=(0,0)時,由式(7)定義的序列y(t)滿足表4所示集合時,構(gòu)造得到的幾乎四進(jìn)制序列是理想平衡幾乎四進(jìn)制序列,且其相關(guān)函數(shù)值如式(18)所示。 表4 滿足推論1的序列y(t)的參數(shù)集合 證明推論1的證明與定理1的證明類似,在此省略。 例2設(shè)q=5=4×1+1=4×12+1,取θ=2,可以得到 當(dāng)(a0,a1,a2,a3,)=(0,0,0,0),(j0,j1,j2,j3,)=(0,1,2,3),(b0,b1,b2,b3,)=(1,1,1,1),(l0,l1,l2,l3,)=(0,3,2,1)時,根據(jù)推論1,可以得到 且其相關(guān)函數(shù)值為 因此,序列y是平衡的理想幾乎四進(jìn)制序列。 推論1是對定理1方法的補充,即當(dāng)q=4f+1=4m2+n2,其中m為奇數(shù),n=1的情況,這些特殊長度除了滿足定理1的構(gòu)造方法外,還滿足推論1的構(gòu)造方法。 定理1與推論1是在四進(jìn)制序列中引入了2個0元素,即(y(0),y(q))=(0,0),接下來的定理2中通過引入一個0元素,即y(0)和y(q)其中有一個為0,同樣,可以得到自相關(guān)函數(shù)旁瓣值的最大模值為2的平衡理想幾乎四進(jìn)制序列。 定理2設(shè)q=4f+1=4m2+n2為一奇素數(shù),其中,f、m、n都是正整數(shù),當(dāng)(y(0),y(q))的取值只有一個為0時,由式(7)定義的序列y(t)滿足(a0,a1,a2,a3)=(0,1,0,1),(b0,b1,b2,b3)=(0,1,0,1)和表5所示集合時,構(gòu)造得到的幾乎四進(jìn)制序列是平衡理想幾乎四進(jìn)制序列,且其相關(guān)函數(shù)值如表5所示。和分別為 證明定理2的證明與定理1的證明類似,取(y(0),y(q))=(0,1),(a0,a1,a2,a3,)=(0,1,0,1),(j0,j1,j2,j3,)=(0,0,1,1),(b0,b1,b2,b3,)=(0,1,0,1),(l0,l1,l2,l3,)=(2,2,3,3),根據(jù)定義3可得 由引理4和引理5可得 表5 滿足定理2的序列y(t)的參數(shù)集合 例3q=17=4×4+1=4×22+1,取θ=2,其分圓類和分圓數(shù)與例1相同,此時,若(y(0),y(q))=(0,1),(a0,a1,a2,a3,)=(0,1,0,1),(j0,j1,j2,j3,)=(0,0,1,1),(b0,b1,b2,b3,)=(0,1,0,1),(l0,l1,l2,l3,)=(2,2,3,3),根據(jù)定理2可以得到 且其自相關(guān)函數(shù)值為 例4設(shè)q=5=4×1+1=4×12+12,取θ=2,其分圓類和分圓數(shù)與例2相同,此時,若(y(0),y(q))=(0,i),(a0,a1,a2,a3,)=(0,1,0,1),(j0,j1,j2,j3,)=(0,0,2,1),(b0,b1,b2,b3,)=(0,1,0,1),(l0,l1,l2,l3,)=(1,3,3,2),根據(jù)定理2可以得到 且其自相關(guān)函數(shù)值為 通過在四進(jìn)制序列中引入一個或2個0元素的思想,基于四階分圓類和中國剩余定理,本文得到了許多新的周期長度為2q(q為奇素數(shù))的平衡理想幾乎四進(jìn)制序列。表6列出了目前已有的偶數(shù)長理想四進(jìn)制序列同本文得到的理想幾乎四進(jìn)制序列在構(gòu)造方法和性能特性方面的對比結(jié)果。由表6可知,本文得到的所有幾乎四進(jìn)制序列的Rmax=2,滿足文獻(xiàn)[5]中給出的理論界要求,且都具有很好的平衡性。與文獻(xiàn)[5-8]相比,文獻(xiàn)[5-8]得到的理想四進(jìn)制序列都是由特殊的二進(jìn)制序列進(jìn)行逆gray映射得到的,且文獻(xiàn)[9]得到的四進(jìn)制序列是幾乎平衡的。而本文提出的構(gòu)造方法是一種直接構(gòu)造,性能特性不受所采用的二進(jìn)制序列特性限制,都是平衡的;與文獻(xiàn)[9-10]相比,雖采用的都是分圓類方法,但是文獻(xiàn)[9]得到的四進(jìn)制序列的,不滿足理想四進(jìn)制序列的理論界,文獻(xiàn)[10]的序列雖然滿足理想四進(jìn)制序列的理論界,但是存在空間相當(dāng)有限,在q≤100內(nèi)僅存在q=5,13,17,29,53這5種情況,而通過本文方法可將q的范圍擴(kuò)展到q=5,13,17,29,37,41,53,61,73,89,97。所以通過本文構(gòu)造方法,可以得到更多平衡的理想四進(jìn)制序列,為實際工程應(yīng)用和通信系統(tǒng)提供了更多的可供選擇的信號范圍。 表6 現(xiàn)有的偶數(shù)長(幾乎)四進(jìn)制序列的比較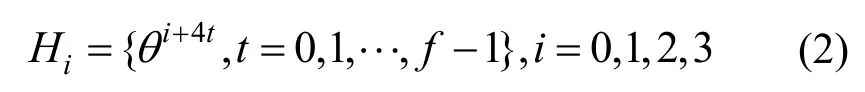
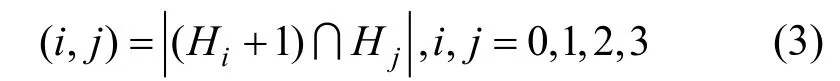
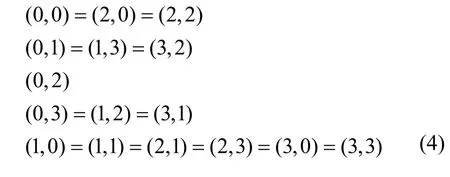

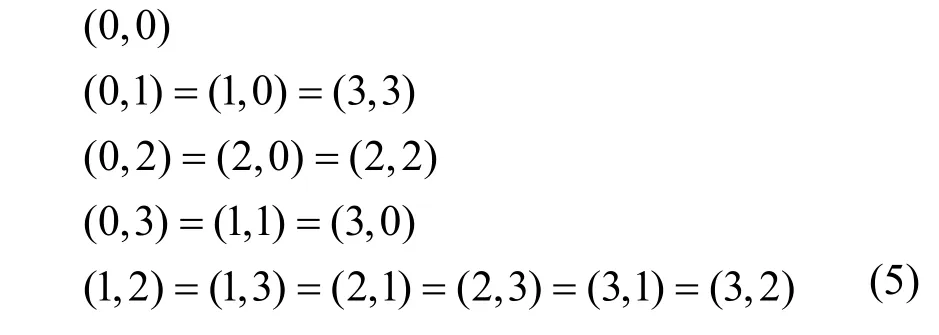

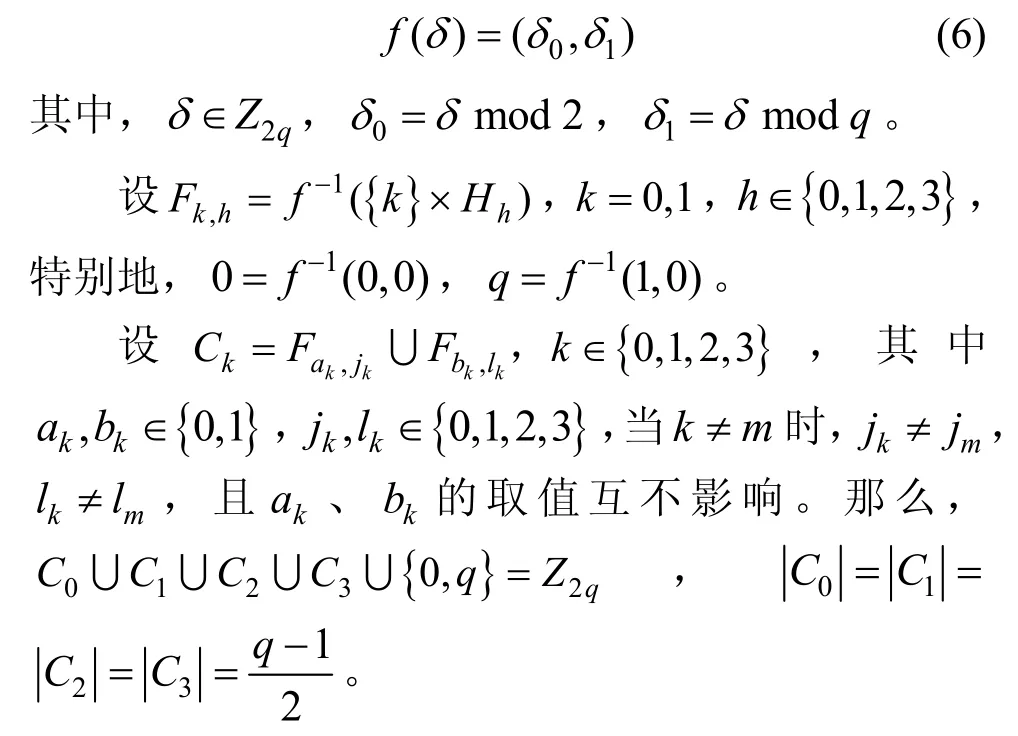
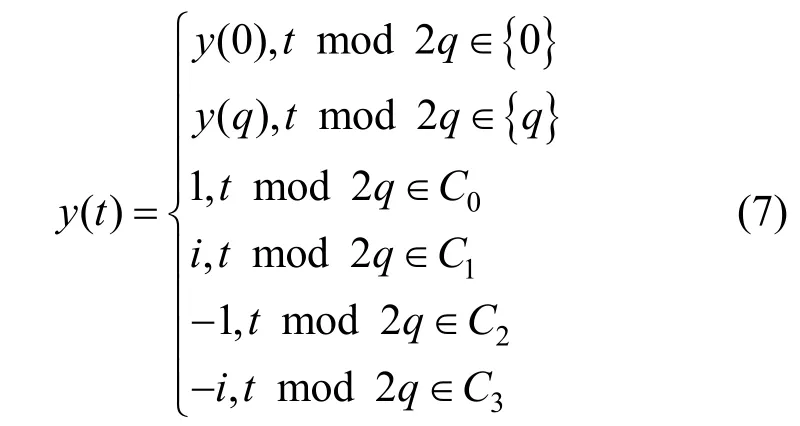
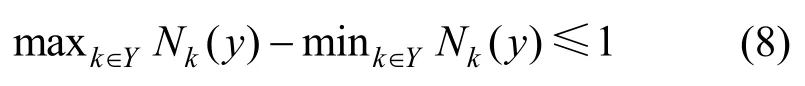
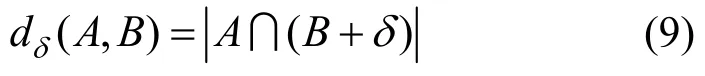

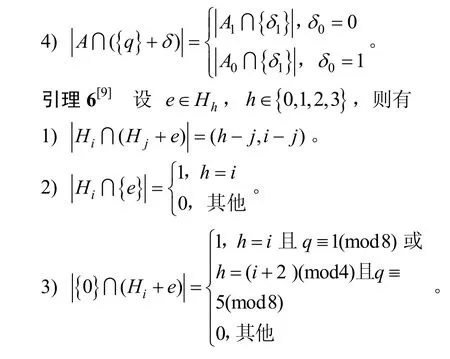
3 理想幾乎四進(jìn)制序列構(gòu)造
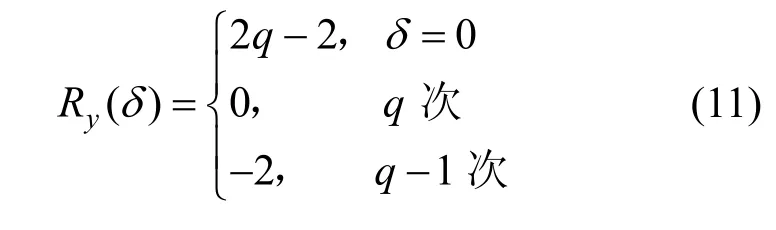
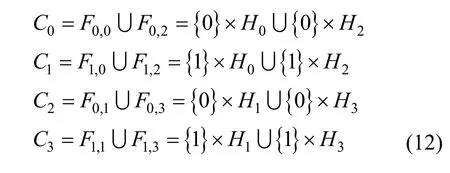
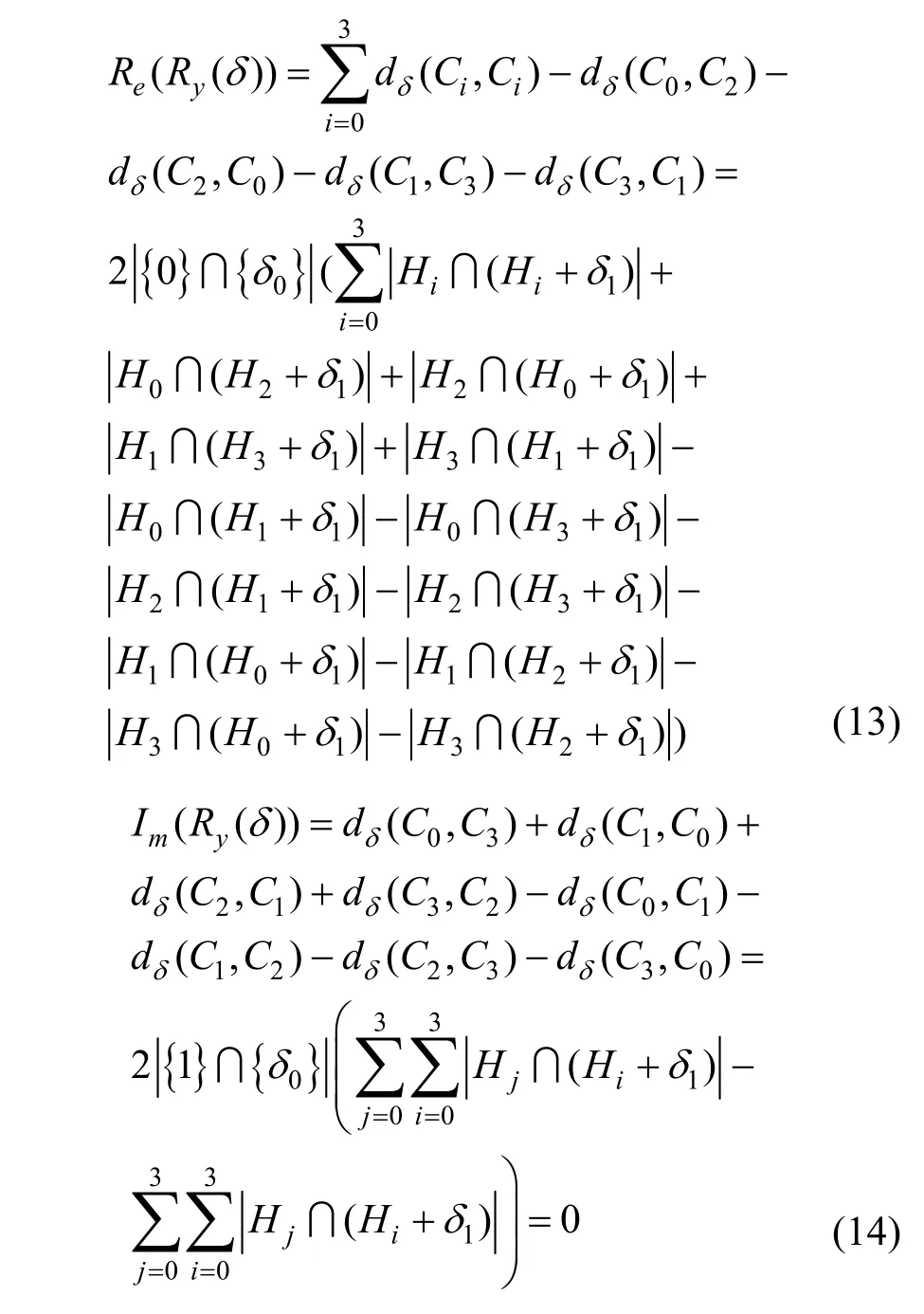
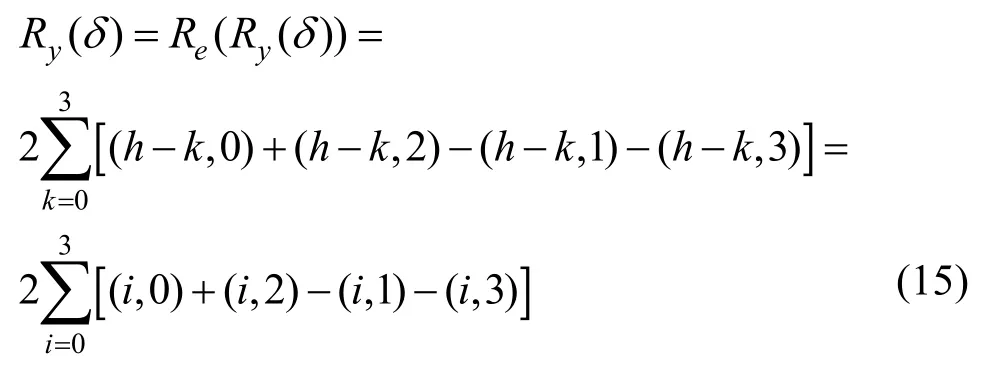

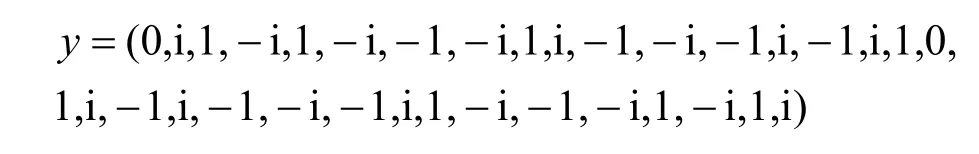
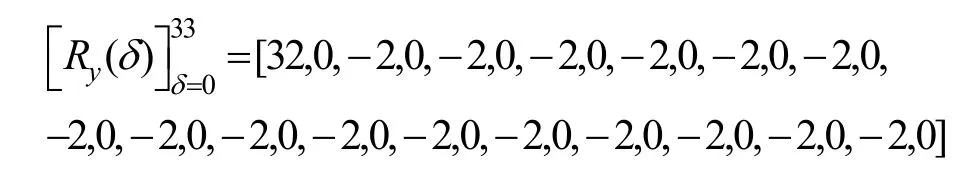
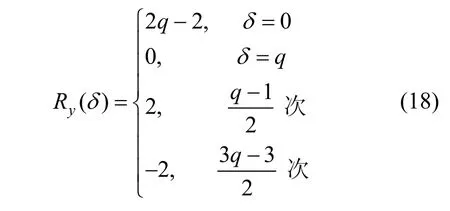


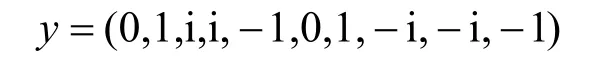
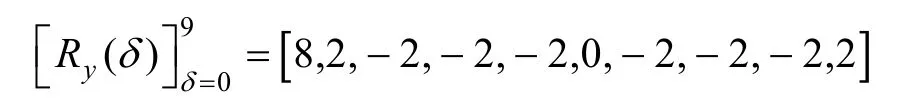
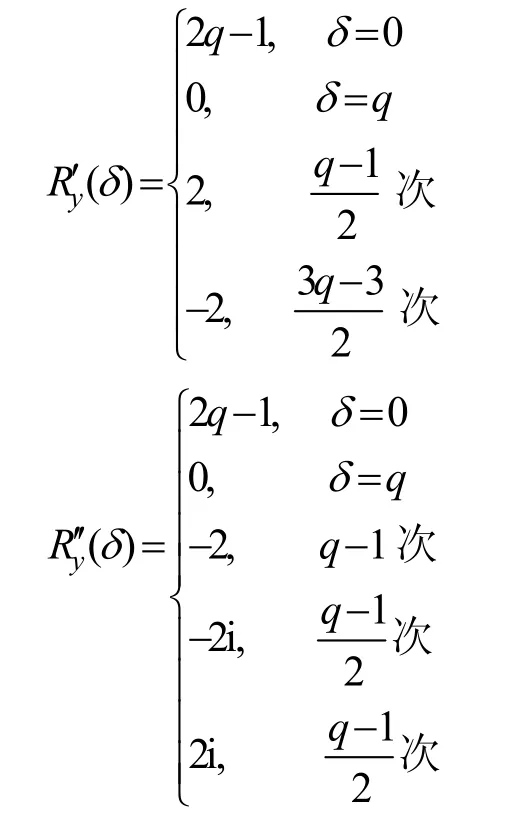
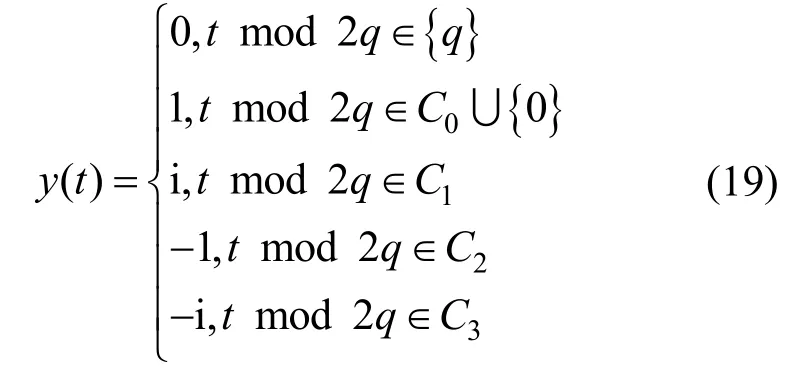


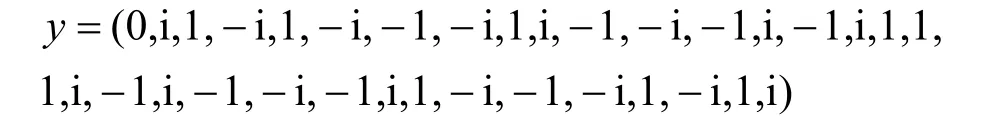
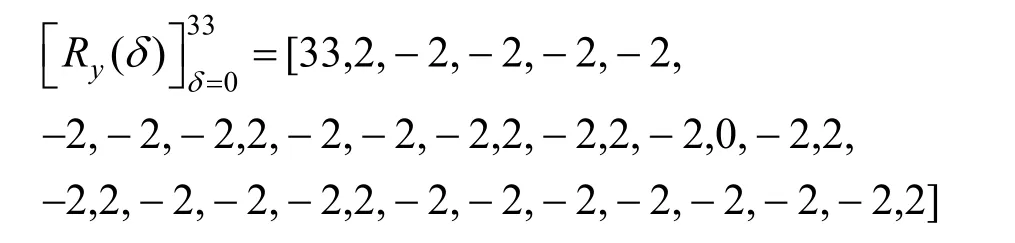
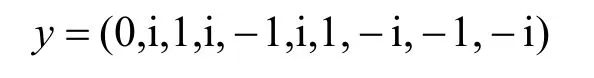
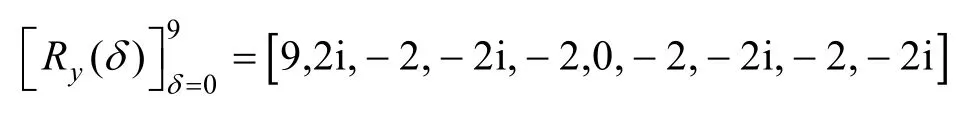
4 結(jié)束語