接觸線雙目視覺測量系統(tǒng)標(biāo)定及立體校正方法研究

（青島大學(xué) 機電工程學(xué)院，青島 266071）

0 引言

接觸線是沿電氣化鐵路鋼軌上空“之”字形架設(shè)的高壓輸電線，它通過與電力機車上的受電弓滑板滑動摩擦直接向電力機車輸送電能。接觸線的高度（導(dǎo)高）、拉出值及其與受電弓滑板接觸部分的磨損直接影響電力機車的受流質(zhì)量和機車的安全運行[1]。因此，在電氣化鐵路建設(shè)和運營維護(hù)過程中，對接觸線進(jìn)行快速、準(zhǔn)確的檢測是必不可少的。綜觀已有的各種檢測方法[2,3]，雙目視覺法是最具潛力的方法，它不僅具有非接觸、速度快、柔性好等優(yōu)點，而且具有檢測接觸線磨損的能力[4]。但由于接觸線距離遠(yuǎn)（導(dǎo)高5370～6450mm）和戶外測量易受干擾等原因，要實現(xiàn)接觸線的高精度檢測，雙目測量系統(tǒng)的結(jié)構(gòu)設(shè)計與參數(shù)標(biāo)定非常關(guān)鍵。本文采用張正友的平面模板兩步法[5,6]，結(jié)合接觸線檢測的技術(shù)特點，對雙目測量系統(tǒng)的參數(shù)標(biāo)定、相機畸變補償和立體矯正進(jìn)行理論分析與實驗研究，為實際測量系統(tǒng)的參數(shù)優(yōu)化設(shè)計與儀器開發(fā)提供理論依據(jù)與實驗參考。

1 接觸線雙目視覺測量原理

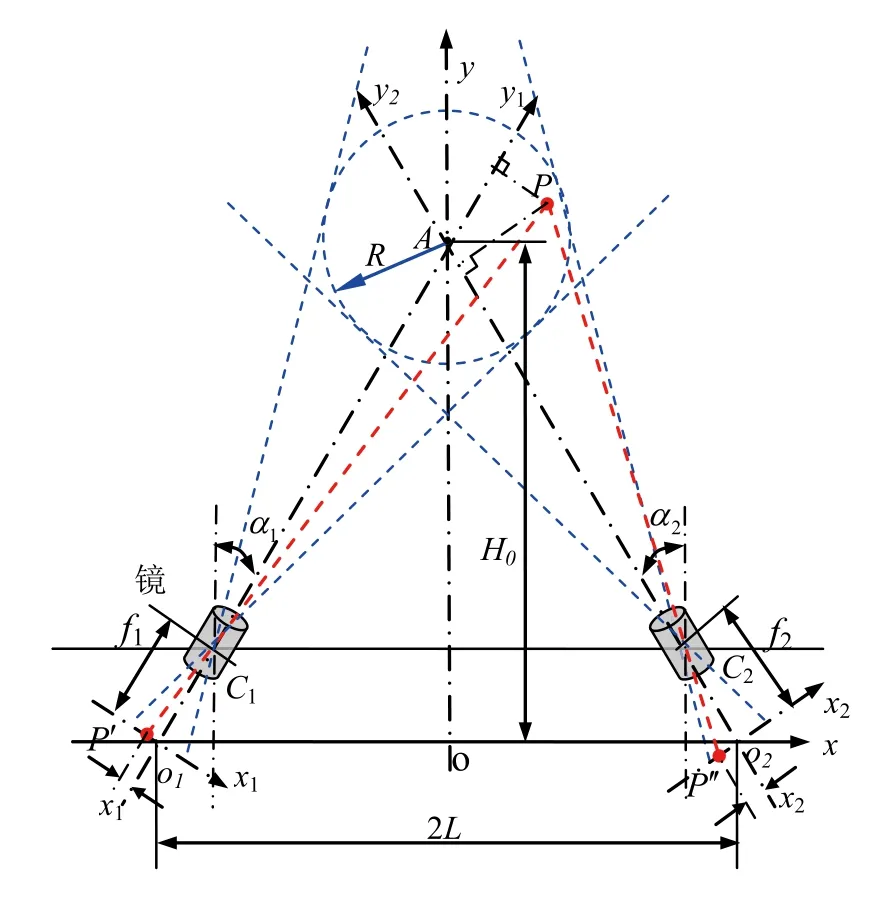
圖1 接觸線雙目視覺測量系統(tǒng)示意圖

基于雙目立體視覺的接觸線檢測系統(tǒng)如圖1所示。兩個結(jié)構(gòu)和性能參數(shù)相同（名義上相同，實際上很難做到完全相同）的面陣CCD相機對稱地分布在豎直平面的兩側(cè)構(gòu)成雙目視覺測量系統(tǒng)。其中，f1、f2為左、右相機鏡頭焦距，α1、α2為左、右相機光軸的傾斜角度，理論上應(yīng)有f1=f2、α1=α2，但實際上難以實現(xiàn)。2L為兩相機像平面中心的距離。為確定被測對象的空間位置，建立坐標(biāo)系如下：1）測量系統(tǒng)坐標(biāo)系xoy：以兩個面陣CCD光敏面中心o1和o2連線的中點o為原點，連線o1o2為x軸，方向由o1指向o2為正；y軸豎直向上為正；2）相機坐標(biāo)系：分別以兩個面陣CCD光敏面中心o1和o2為原點在兩個CCD上建立各自的坐標(biāo)系x1o1y1和x2o2y2。

設(shè)P點為接觸線位置，其在xoy坐標(biāo)系中的坐標(biāo)為（x，y）；P'（x1，0）和P''（x2，0）分別為P點在兩相機像平面上成像點坐標(biāo)。根據(jù)幾何光學(xué)成像原理，可導(dǎo)出：

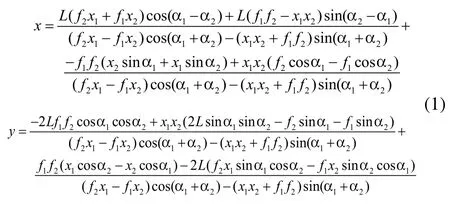
可見，P點坐標(biāo)（x，y）取決于x1、x2、f1、f2、α1、α2和L這7個參數(shù)。其中任一參數(shù)的誤差均會引起測量誤差。因此，必須對測量系統(tǒng)進(jìn)行標(biāo)定與立體矯正。

1）f1、f2、α1、α2和L為系統(tǒng)設(shè)計的理論值，而實際值相對理論值總是有偏差的，進(jìn)行標(biāo)定的目的就是要盡可能準(zhǔn)確地確定實際值的大小。

2）式(1)是按幾何光學(xué)理想成像公式導(dǎo)出的，沒有考慮成像畸變。因此，需要進(jìn)行畸變補償，以減小由x1、x2引起的測量誤差。

3）理想情況下，兩個相機的光軸應(yīng)該共面、而且像平面行對齊，但實際中難以實現(xiàn)，立體校正將實際中非共面非行對齊的兩幅圖像校正成共面行對齊，可減小這一誤差對測量的影響。

2 雙目視覺測量系統(tǒng)標(biāo)定方法

2.1 相機成像模型

為建立簡化的相機模型，將鏡頭的通光孔徑看做一個小孔，理論上這并不影響成像結(jié)果，因此可以只考慮鏡頭光心位置處的光線。一般情況下，相機成像的物距遠(yuǎn)大于像距。根據(jù)高斯公式[7]，可近似認(rèn)為相機鏡頭的焦點在成像平面上，物、像的方向是相反的。為了簡化數(shù)學(xué)運算，將原成像平面平移到與物點同側(cè)。雖然從物理學(xué)的角度來看這是不可行的，但從數(shù)學(xué)運算的角度進(jìn)行分析，它們是等價的。簡化后得到的成像模型就是針孔相機模型[8]，如圖2所示。圖中，OcXcYcZc為相機坐標(biāo)系，坐標(biāo)原點為相機光心Oc；o1xy為圖像物理坐標(biāo)系，坐標(biāo)原點為相機主軸與圖像平面的交點o1；x軸、y軸與Xc、Yc軸平行同向。由三角形相似性可得基本投影等式：x=fXc/Zc，y=fYc/Zc。

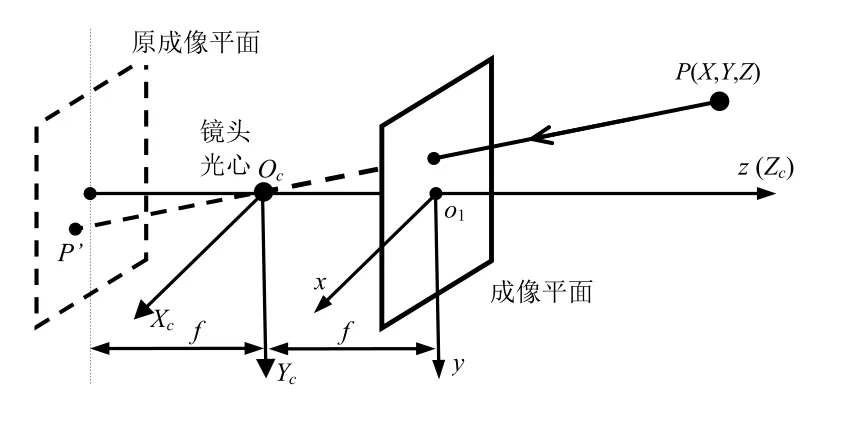
圖2 針孔相機模型示意圖

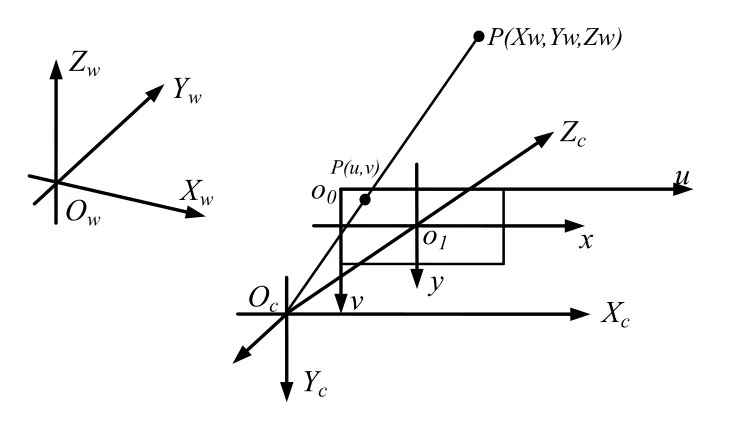
圖3 坐標(biāo)系關(guān)系示意圖

2.2 相機標(biāo)定

標(biāo)定是指建立實際場景點的三維坐標(biāo)與相機二維投影圖像坐標(biāo)之間的關(guān)系，進(jìn)而求解相機參數(shù)（包括內(nèi)參、外參及畸變系數(shù)）實際值的過程[9]。首先定義4個坐標(biāo)系，如圖3所示。1）世界坐標(biāo)系OwXwYwZw，描述物體在三維空間中的位置；2）相機坐標(biāo)系OcXcYcZc，同圖2；3）圖像物理坐標(biāo)系o1xy，同圖2；4）像素坐標(biāo)系o0uv，即將圖像物理坐標(biāo)點用像素的形式表示，坐標(biāo)原點在CCD圖像平面的左上角，用o0表示。

具體標(biāo)定過程是：世界坐標(biāo)系通過旋轉(zhuǎn)平移變換到相機坐標(biāo)系，相機坐標(biāo)系通過投影變換到圖像物理坐標(biāo)系，圖像物理坐標(biāo)系再通過像素轉(zhuǎn)換到像素坐標(biāo)系。這一坐標(biāo)變換過程的數(shù)學(xué)描述如下：

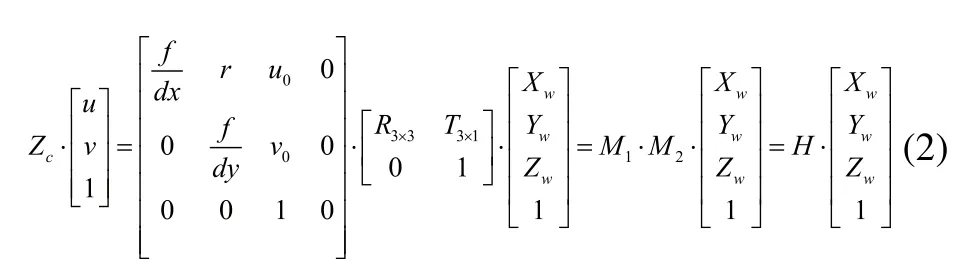
式中，M1為包含內(nèi)部參數(shù)的3×4矩陣；M2為4×4外部參數(shù)矩陣；H=M1·M2為單應(yīng)性矩陣；f/dx、f/dy分別是u軸與v軸的有效焦距；r是圖像橫向u坐標(biāo)與縱向V坐標(biāo)軸的不垂直因子，一般可忽略，記為0；u0、v0是主點的像素坐標(biāo)；R3×3、T3×1表示相機坐標(biāo)系相對于世界坐標(biāo)系的位置關(guān)系[10]。

以上是不考慮鏡頭畸變的情況，然而鏡頭畸變是一個不可忽略的因素。畸變主要有徑向畸變和切向畸變，而且以徑向畸變?yōu)橹鱗5]。設(shè)未考慮成像畸變時像點的物理坐標(biāo)為（x，y），考慮畸變時的實際成像點坐標(biāo)為（xd，yd），則有：

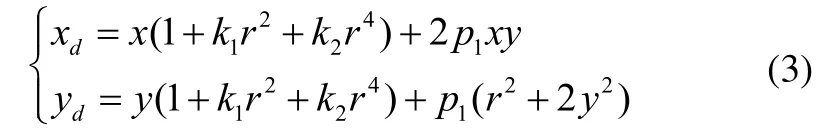
式中，r2=x2+y2，k1、k2分別為初級和二級徑向畸變系數(shù)；p1為初級切向畸變系數(shù)。

由于相機標(biāo)定所采用的棋盤格標(biāo)定板是一個平面板，將世界坐標(biāo)系構(gòu)造在標(biāo)定板平面上，即令標(biāo)定板平面為ZW=0的平面，則可將H化為3×3的齊次矩陣，其中有8個未知量，至少需要8個方程方可求解。而一對物像共軛點（Xw，Yw）與（u，v）可以提供兩個方程，故需要4對物像共軛點，便可以計算出世界坐標(biāo)平面到圖像坐標(biāo)平面的單應(yīng)性矩陣H，因此每幅棋盤格標(biāo)定板至少需要提供4個有用的物點，即角點。通過數(shù)學(xué)計算后得到內(nèi)參數(shù)矩陣M1與單應(yīng)性矩陣中列向量h1、h2之間的關(guān)系：

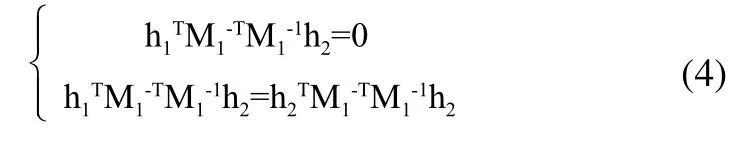
式中，h1、h2已知，而M1中含有5個未知量，因此至少需要3個不同的單應(yīng)性矩陣產(chǎn)生6個方程來求解內(nèi)參數(shù)矩陣。而外參數(shù)矩陣M2可由單應(yīng)性矩陣與內(nèi)參數(shù)矩陣M1求得。

以上分析表明，理論上，單相機內(nèi)參數(shù)和外參數(shù)的標(biāo)定至少需要拍攝3幅不同方位的棋盤格圖像。但由于實際采集的圖像不可避免存在噪聲，為了得到高質(zhì)量結(jié)果，一般需要采集多于10幅不同方位的7×8或者更大棋盤格的圖像,再通過最大似然估計對得到的結(jié)果進(jìn)行優(yōu)化，以提高標(biāo)定精度。

在獲得M1和M2的標(biāo)定結(jié)果后，由式(2)求得沒有畸變時圖像物理坐標(biāo)（x，y），然后將拍攝的n幅圖像每幅取m個角點，可以構(gòu)成n·m個如式(3)所示的方程組。利用最小二乘法可求得畸變系數(shù)k1、k2、p1。最后，建立如式(5)所示的目標(biāo)函數(shù)，通過Levenberg-Marquarat算法進(jìn)行優(yōu)化，得到優(yōu)化的畸變系數(shù)。

式中，mij表示第i幅圖像上的第j個角點的像點坐標(biāo)，m'（M1，k1，k2，p1，Ri，Ti，Mj）表示加入畸變系數(shù)k1、k2、p1后，第i幅圖像上的第j個角點的世界坐標(biāo)Wj通過Ri的旋轉(zhuǎn)與Ti平移后得到的像點坐標(biāo)。利用同一個標(biāo)定板同時對兩個相機進(jìn)行標(biāo)定，分別得到二者相對同一坐標(biāo)系的旋轉(zhuǎn)矩陣和平移向量這一過程就是雙目標(biāo)定的過程。本文設(shè)定左相機坐標(biāo)系為參考坐標(biāo)系，用R、T表示右相機相對于左相機的旋轉(zhuǎn)矩陣和平移向量，則有：

式中，Rl、Tl、Rr、Tr分別為世界坐標(biāo)系中一點相對于左、右相機的旋轉(zhuǎn)矩陣與平移向量，通過單相機標(biāo)定獲得。由于圖像采集過程中噪聲的存在，利用兩個相機同時拍攝標(biāo)定板后，采集的每一組圖像對計算得到的R、T都會有一定偏差，為使計算得到的R、T值更加準(zhǔn)確，可通過Levenberg-Marquardt算法，取所有圖像對中計算得到的R、T的中值來作為初始近似值進(jìn)行非線性優(yōu)化，得到準(zhǔn)確的結(jié)果。

3 Bouguet立體校正方法

由于實際的雙目測量系統(tǒng)不可避免地存在結(jié)構(gòu)參數(shù)誤差及相機自身參數(shù)誤差，因此左、右兩相機同時獲取的同一目標(biāo)的兩幅圖像一般是非共面、非行對齊。立體校正的目的就是將這兩幅圖像校正成共面、且行對齊，以便于后續(xù)特征匹配與測距[11]。Bouguet算法利用標(biāo)定得到的相機內(nèi)外參數(shù)，首先對圖像進(jìn)行畸變校正，使得左右兩幅圖像投影畸變達(dá)到最小，實現(xiàn)圖像觀測面積最大化。然后，將選擇矩陣R分成兩個對等的矩陣，使兩幅圖像均旋轉(zhuǎn)一半，達(dá)到兩幅圖像在同一個成像面上的效果。最后，結(jié)合平移矩陣T使得同一成像平面上的左右兩幅圖像極線平移成同一行，并且與基線平行[10]。Bouguet校正算法正是利用相機內(nèi)、外參數(shù)以及畸變系數(shù)的標(biāo)定結(jié)果進(jìn)行立體校正，如圖4所示。

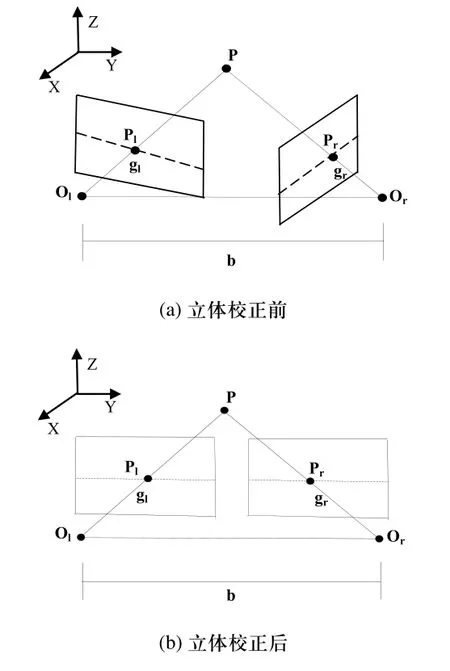
圖4 Bouguet立體校正示意圖

4 標(biāo)定實驗及結(jié)果評價

4.1 雙目測量實驗系統(tǒng)的組成

雙目測量系統(tǒng)及其標(biāo)定實驗如圖5所示。該系統(tǒng)由兩個FC-IU320C-6型工業(yè)相機組成，鏡頭為FUJINON HF25HA-1B定焦鏡頭，焦距f=25mm，分辨率為2048×1536，像元大小為3.2μm×3.2μm。兩個相機分別安裝在兩個“球型云臺+板型云臺”的組合云臺上。兩個組合云臺分別固定在底座（由100mm×48 mm×5.3mm槽鋼制作）的兩端。球型云臺和板型云臺均帶有調(diào)節(jié)刻度，方便調(diào)節(jié)兩相機成像平面的中心距2L，使其約等于高速鐵路兩根鋼軌軌距。標(biāo)定所用的平面棋盤格為自制，格數(shù)8×6，每格的尺寸為80mm×80 mm，用A1圖紙打印，粘貼在A0繪圖板上。

圖5 雙目測量系統(tǒng)標(biāo)定實驗場景圖

4.2 標(biāo)定實驗及其結(jié)果分析

標(biāo)定板放置在一個可旋轉(zhuǎn)、可升降、帶滾輪的座椅上，便于調(diào)整距離和轉(zhuǎn)動不同方向。本實驗采集20對（對于同一標(biāo)定板位置，左、右相機各采集一幅圖像為一對）不同方位下的棋盤格標(biāo)定板圖像。標(biāo)定軟件是在Visual Studio 2010開發(fā)環(huán)境下，利用C++自主設(shè)計開發(fā)，程序界面如圖6所示。圖中“左相機”下方輸出3×3矩陣即為左相機內(nèi)參數(shù)矩陣，矩陣中的元素與式(2)中各內(nèi)參數(shù)相對應(yīng)，例如u0為1023.982，v0為768.033。同理，圖中“右相機”下方輸出3×3矩陣即為右相機的內(nèi)參數(shù)矩陣。圖中“雙目標(biāo)定”下方輸出的是右相機相對于左相機的相對位置關(guān)系。

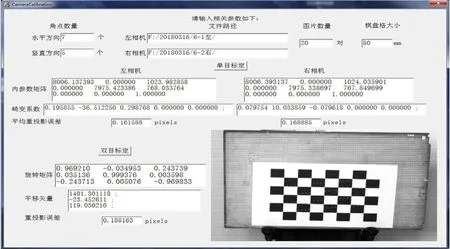
圖6 雙目系統(tǒng)標(biāo)定程序界面

標(biāo)定結(jié)果分析：

由圖6標(biāo)定結(jié)果，計算左相機焦距f1與右相機焦距f2，得焦距f1=8006.137×3.2×10-3≈25.6196mm，f2=8006.393×3.2×10-3≈25.6205mm，即二者偏差很小，但均不等于標(biāo)稱值25mm。左相機光軸與其圖像平面的交點為（1023.982，768.033），右相機光軸與其圖像平面的交點為（1024.035，767.849），兩相機的主點幾乎在圖像平面中心（1024，768）處。標(biāo)定結(jié)果中畸變系數(shù)順序為k1、k2、p1、p2、k3，由于不考慮p2、k3，故二者均為0，兩個相機的畸變系數(shù)k1、p1均較小，k2稍大一些，說明有一定徑向畸變，而切向畸變很小，可以忽略。一般平均重投影誤差小于0.2個像素即可認(rèn)為標(biāo)定結(jié)果不錯，左相機平均重投影誤差為0.161313個像素，右相機平均重投影誤差為0.168885個像素，均小于0.2個像素，說明標(biāo)定結(jié)果良好。

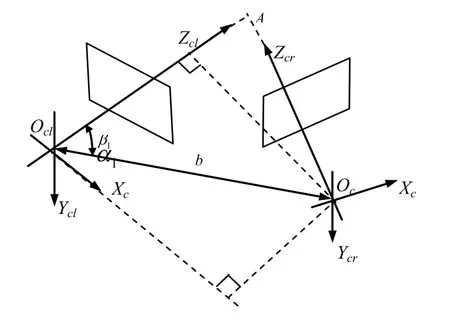
圖7 光心距離與光軸傾斜角求解示意圖

由圖6右相機相對于左相機的位置關(guān)系，可進(jìn)一步求解相機光軸傾角與光心距離，原理圖如圖7所示。

式中β1為左相機光軸傾斜角的余角，由式(7)可以求得β1為85.0018°，則左相機光軸的傾斜角為α1=90°-β1=4.998°，同理，知道左相機相對于右相機的位置關(guān)系后求得右相機光軸傾角為α2=4.978°；由式(7)可以求得兩個相機光心之間的距離為b=1406.65mm。以上求出的值，與實驗中設(shè)定（通過仔細(xì)調(diào)節(jié)實驗裝置來設(shè)定，肯定有誤差）的兩個相機光軸傾角為5°和兩個相機光心距離為1405mm非常接近，表明標(biāo)定結(jié)果良好。

4.3 Bouguet立體校正

在完成雙目測量系統(tǒng)標(biāo)定后，利用所得到的標(biāo)定結(jié)果進(jìn)行Bouguet立體校正。校正程序也是在Visual Studio 2010開發(fā)環(huán)境下，利用C++自主設(shè)計開發(fā)。通過對左、右相機拍攝的一個圖像對進(jìn)行處理，得到圖8所示的校正結(jié)果。由圖可見，校正前左、右圖像非共面且行不對齊；校正后，兩幅圖像實現(xiàn)了良好的共面與行對齊，證明了標(biāo)定結(jié)果的準(zhǔn)確性。

圖8 Bouguet立體校正結(jié)果圖

5 結(jié)論

本文對接觸線雙目視覺測量系統(tǒng)的標(biāo)定與立體校正問題進(jìn)行了分析研究，結(jié)果表明：1）針對本文涉及的高鐵接觸線檢測應(yīng)用，采用張正友的平面模板兩步法進(jìn)行相機的內(nèi)、外參數(shù)標(biāo)定，左、右兩相機的平均重投影誤差均小于0.2個像素，達(dá)到了比較理想的標(biāo)定精度。Bouguet立體校正所得到的結(jié)果也充分驗證了這一點。因為Bouguet立體校正是在標(biāo)定結(jié)果的基礎(chǔ)上進(jìn)行的，標(biāo)定結(jié)果的誤差將直接導(dǎo)致Bouguet立體校正結(jié)果不理想。2）相機鏡頭的徑向畸變遠(yuǎn)大于切向畸變，后者通常可以忽略。3）文中的標(biāo)定與校正方法及所開發(fā)的雙目測量系統(tǒng)標(biāo)定與立體校正軟件可推廣應(yīng)用到類似的雙目測量系統(tǒng)。