行星傳動(dòng)動(dòng)態(tài)嚙合有限元仿真分析

（西安科技大學(xué) 機(jī)械工程學(xué)院，西安 710054）

0 引言

行星輪系工作可靠，傳動(dòng)效率高，適用范圍廣，要保持平穩(wěn)的齒輪嚙合傳動(dòng)過程，有必要對齒輪進(jìn)行強(qiáng)度分析。嚙合是一種典型的接觸問題。在若干假設(shè)前提下，傳統(tǒng)的齒輪的接觸強(qiáng)度計(jì)算不能準(zhǔn)確反映嚙合過程中的應(yīng)力以及應(yīng)變分布與變化。而齒輪在實(shí)際傳動(dòng)過程中兩齒面的接觸區(qū)域是不斷發(fā)生變化的，采用有限元分析方法則可以準(zhǔn)確、快速計(jì)算，直觀方便的查看計(jì)算的接觸應(yīng)力分布等優(yōu)點(diǎn)。

本文運(yùn)用ABAQUS軟件，基于經(jīng)典赫茲接觸理論，分別采用準(zhǔn)靜態(tài)分析方法與顯示動(dòng)力分析模擬行星齒輪傳動(dòng)中輪齒嚙合情況，研究輪齒接觸應(yīng)力與齒根應(yīng)力分布規(guī)律，對比兩種方法與理論分析，可以為行星輪系設(shè)計(jì)提供更為可靠的設(shè)計(jì)保證。

1 傳統(tǒng)理論應(yīng)力分析

齒輪的失效形式主要是齒面損傷和輪齒折斷。工作時(shí)，各個(gè)輪齒表面接觸應(yīng)力是按脈動(dòng)循環(huán)變化的，若齒面最大接觸應(yīng)力大于材料的接觸應(yīng)力極限，則在多次重復(fù)載荷作用下，齒輪表面會(huì)逐漸產(chǎn)生細(xì)小的裂紋，裂紋慢慢擴(kuò)展，甚至?xí)纬善邳c(diǎn)蝕，對傳動(dòng)的穩(wěn)定性有很大的影響，伴隨著產(chǎn)生振動(dòng)和噪聲，影響齒輪的正常工作，甚至?xí)瘕X輪的破壞。另外，在行星齒輪傳動(dòng)中，當(dāng)輪齒受到載荷的反復(fù)作用，齒根彎曲應(yīng)力大于材料的彎曲應(yīng)力極限時(shí)，齒根部分將產(chǎn)生疲勞裂紋，隨著裂紋不斷擴(kuò)展，最終輪齒產(chǎn)生疲勞折斷。基于這兩種失效形式，故對齒輪的接觸強(qiáng)度與齒根彎曲疲勞強(qiáng)度進(jìn)行強(qiáng)度校核。

1.1 齒輪接觸應(yīng)力計(jì)算

兩物體相互接觸時(shí)，在接觸區(qū)域附近會(huì)產(chǎn)生局部應(yīng)力和局部變形，稱為接觸應(yīng)力和接觸變形，本文采用經(jīng)典赫茲接觸理論來進(jìn)行齒輪的接觸應(yīng)力的計(jì)算，齒輪嚙合時(shí)，可將齒廓嚙合點(diǎn)的曲率半徑視為接觸圓柱體的半徑，齒輪節(jié)點(diǎn)處一般只有一對齒嚙合，節(jié)線附近的齒根表面往往先出現(xiàn)點(diǎn)蝕。因此接觸疲勞強(qiáng)度計(jì)算通常以節(jié)點(diǎn)為計(jì)算點(diǎn)，可得接觸應(yīng)力公式：

其中由機(jī)械手冊中可查出：

K為載荷系數(shù)；

ZE為彈性系數(shù)；

ZH為節(jié)點(diǎn)區(qū)域系數(shù)；

Zε為重合度系數(shù)；

d1為小齒輪的分度圓直徑；

u為大小齒輪齒數(shù)之比；

T1為主動(dòng)輪的扭矩。

許用接觸應(yīng)力：

式中：σHlim為失效概率為1%時(shí)，試驗(yàn)齒輪的接觸疲勞極限；

SHmin為接觸強(qiáng)度的最小安全系數(shù)；

ZN為接觸疲勞強(qiáng)度極限，均可由機(jī)械設(shè)計(jì)手冊查出。

1.2 齒根彎曲疲勞強(qiáng)度計(jì)算

由于輪緣剛度很大，故將輪齒視為是具有一定寬度的懸臂梁。理論上載荷應(yīng)由同時(shí)嚙合的多對齒分擔(dān)，為簡化計(jì)算，通常假設(shè)載荷只作用于只有一對齒嚙合時(shí)的齒頂進(jìn)行分析，并采用重合度系數(shù)予以修正。在載荷長期作用下，輪齒齒根受拉一側(cè)先產(chǎn)生疲勞裂紋，故齒根彎曲疲勞強(qiáng)度以受拉側(cè)為計(jì)算依據(jù)。齒根彎曲強(qiáng)度校核公式：

單向受載時(shí)，許用彎曲應(yīng)力公式：

將中心輪、行星輪、內(nèi)齒輪的各個(gè)相應(yīng)參數(shù)代入式(1)～式(4)計(jì)算可得各齒輪的接觸應(yīng)力和彎曲應(yīng)力。

2 有限元分析模型構(gòu)建

太陽輪與行星齒輪的接觸和行星齒輪與內(nèi)齒輪的接觸都存在相對運(yùn)動(dòng)的摩擦力，由于摩擦力相對正壓力很小，所以在分析過程中設(shè)定摩擦系數(shù)。在有限元分析中，接觸過程通常依賴于時(shí)間，且在接觸界面上運(yùn)動(dòng)學(xué)和動(dòng)力學(xué)的狀態(tài)是事前未知的。本文主要是利用ABAQUS對行星齒輪傳動(dòng)機(jī)構(gòu)進(jìn)行齒輪嚙合的接觸分析，查看傳動(dòng)過程中齒面接觸應(yīng)力。

2.1 Abaqus有限元分析前處理

齒輪有限元分析屬于結(jié)構(gòu)分析，初始狀態(tài)下模型的響應(yīng)由線彈性模型確定，材料定義為各向同性，并通過輸入彈性模量、泊松比、和質(zhì)量密度三個(gè)物理量來完成材料屬性定義。本文中心輪和行星輪均采用20CrMnTi，齒面硬度58～62HRC，滲碳淬火，加工精度6級(jí)。內(nèi)齒圈均采用42CrMo，加工精度7級(jí)。材料屬性如表1所示。

表1 材料屬性表

網(wǎng)格劃分是否合理影響分析結(jié)果精度，網(wǎng)格過疏結(jié)果誤差較大，網(wǎng)格過密計(jì)算機(jī)工作量較大耗時(shí)長。由于行星輪結(jié)構(gòu)較為復(fù)雜，本文簡化模型分析單齒的嚙合，在劃分網(wǎng)格時(shí)采用結(jié)構(gòu)化網(wǎng)格和局部網(wǎng)格細(xì)化技術(shù)，在接觸面附近設(shè)置較密種子，既減少網(wǎng)格數(shù)量又減小了分析誤差劃分。網(wǎng)格單元類型為C3D8R，單元個(gè)數(shù)為，網(wǎng)格劃分模型如下圖所示。

根據(jù)行星輪傳動(dòng)機(jī)構(gòu)的實(shí)際工況進(jìn)行邊界條件設(shè)置，約束內(nèi)齒輪所有自由度，釋放太陽輪繞軸線的旋轉(zhuǎn)自由度，約束其他自由度，行星輪既可以繞其軸線旋轉(zhuǎn)，又可以繞太陽輪旋轉(zhuǎn)，因此釋放切向位移和周向旋轉(zhuǎn)位移。

2.2 準(zhǔn)靜態(tài)接觸分析

ABAQUS/Standard采用Newton-Raphson算法求解非線性問題的，把分析過程劃分為一系列的載荷增量步，在每個(gè)增量步內(nèi)進(jìn)行多次迭代，得到合理的解釋后再求解下一個(gè)增量步，所有增量響應(yīng)的總和就是非線性分析的近似解。

在齒輪接觸分析前處理過程中，建立在接觸關(guān)系初期直接施加力載荷，往往會(huì)導(dǎo)致分析計(jì)算不收斂，因此通過設(shè)置多個(gè)非線性靜態(tài)通用步模擬行星輪系的動(dòng)態(tài)分析，首先使用位移邊界條件建立平穩(wěn)接觸，然后施加力載荷。

準(zhǔn)靜態(tài)模擬齒輪嚙合傳動(dòng)仿真分析結(jié)果如下圖所示，從分析云圖中可以清楚地看到齒輪入嚙到脫嚙時(shí)接觸應(yīng)力大小位置與變化情況。隨著齒輪副的進(jìn)一步嚙合，齒輪副在嚙合點(diǎn)和齒根位置的應(yīng)力較大，且太陽輪和行星輪嚙合部分的齒面接觸應(yīng)力最大值為420.7 MPa，行星輪和內(nèi)齒輪嚙合部分的齒面接觸應(yīng)力最大為373.4MPa，應(yīng)力云圖如圖1、圖2所示。

圖1 內(nèi)齒圈和行星輪嚙合齒面接觸應(yīng)力

圖2 太陽輪和行星輪嚙合齒面接觸應(yīng)力

由于篇幅限制，在此僅列出0.14s、0.43s、0.71s 、1.00s時(shí)刻行星輪傳動(dòng)動(dòng)態(tài)嚙合情況，如圖3～圖6所示，由嚙合云圖可以看出，隨著進(jìn)一步嚙入，太陽輪與行星輪齒面接觸應(yīng)力大于行星輪與內(nèi)齒圈，且接觸應(yīng)力在輪齒接觸點(diǎn)處最大，并向齒根擴(kuò)散。

圖3 0.14s嚙合云圖

圖4 0.43s嚙合云圖

圖5 0.71s嚙合云圖

圖6 1.00s嚙合云圖

在ABAQUS中采用S-Max，Principle模塊可以得到各齒輪的齒根彎曲應(yīng)力大小及分布云圖，其中內(nèi)齒圈、行星輪、太陽輪的齒根彎曲應(yīng)力云圖如圖7～圖9所示。

圖7 內(nèi)齒圈齒根彎曲應(yīng)力云圖

圖8 太陽輪齒根彎曲應(yīng)力云圖

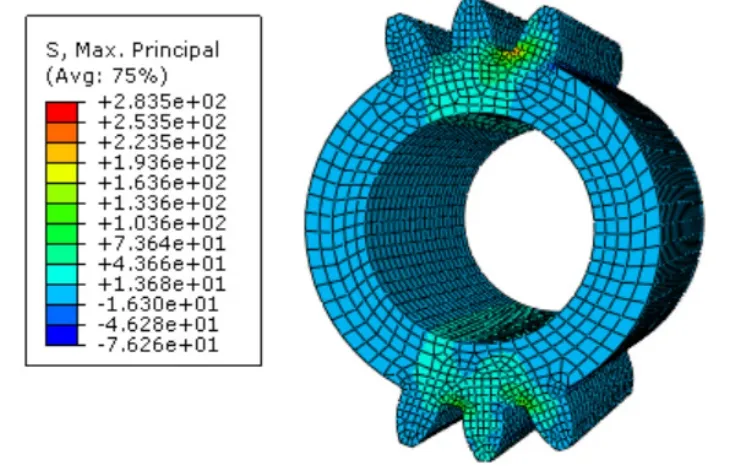
圖9 行星輪齒根彎曲應(yīng)力云圖

從以上應(yīng)力云圖可以看出，內(nèi)齒圈齒根彎曲應(yīng)力244.9MPa，太陽輪齒根彎曲應(yīng)力301.6MPa，行星輪齒根彎曲應(yīng)力283.5MPa。均滿足強(qiáng)度要求。

2.3 顯示動(dòng)力學(xué)分析

ABAQUS/Explicit在求解非線性問題時(shí)不需要進(jìn)行迭代，而是顯示地從上一個(gè)增量步的靜力學(xué)狀態(tài)來推算出動(dòng)力學(xué)平衡方程的解。顯示動(dòng)力分析的求解過程需要大量的增量步，但由于不進(jìn)行迭代，不需要求解全體方程組，并且每個(gè)增量步的計(jì)算成本很小，可以高效地解決復(fù)雜的非線性問題。

在進(jìn)行齒輪模型接觸分析時(shí)，ABAQUS會(huì)自動(dòng)創(chuàng)建一個(gè)初始分析步來定義初始狀態(tài)下的邊界條件和相互作用，為使齒輪穩(wěn)定接觸，并能夠仿真太陽輪的嚙入和嚙出過程，本文創(chuàng)建兩個(gè)動(dòng)態(tài)顯式分析步，第一個(gè)分析步設(shè)為0.005s，第二個(gè)分析步設(shè)為0.06s，Nlgoem選擇ON。為加速分析，降低計(jì)算成本，質(zhì)量放大系數(shù)為10。質(zhì)量放大倍數(shù)越大，計(jì)算速度越快，但同時(shí)也會(huì)使齒輪慣性增大，計(jì)算結(jié)果不夠精確。本分析中應(yīng)力云圖如下所示，其中太陽輪和行星輪嚙合部分的齒面接觸應(yīng)力最大值為473.8MPa，行星輪和內(nèi)齒輪嚙合部分的齒面接觸應(yīng)力最大為511.9MPa。

圖10 內(nèi)齒圈和行星輪嚙合齒面接觸應(yīng)力

本分析同樣列出0.14s、0.43s、0.71s、1.00s時(shí)刻行星輪傳動(dòng)動(dòng)態(tài)嚙合情況，如圖3～圖6所示，由嚙合云圖可以看出，在顯示動(dòng)力學(xué)分析下的輪齒嚙合過程中，接觸應(yīng)力依舊在輪齒接觸點(diǎn)處最大，并向齒根擴(kuò)散。其中太陽輪與行星輪嚙合處、行星輪與內(nèi)齒圈嚙合處均出現(xiàn)最大應(yīng)力點(diǎn)。

圖11 太陽輪和行星輪嚙合齒面接觸應(yīng)力

圖12 0.14s嚙合云圖

圖13 0.43s嚙合云圖

圖14 0.71s嚙合云圖

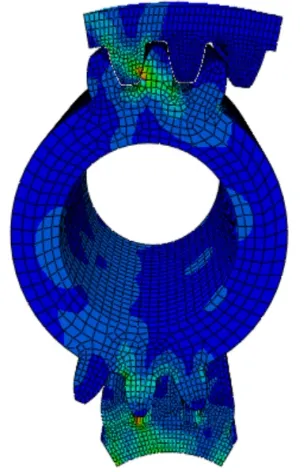
圖15 1.00s嚙合云圖

采用S-Max，Principle模塊得到各齒輪的齒根彎曲應(yīng)力大小及分布云圖，其中內(nèi)齒圈、行星輪、太陽輪的齒根彎曲應(yīng)力云圖如圖7～圖9所示。

圖16 內(nèi)齒圈齒根彎曲應(yīng)力云圖

圖17 行星輪齒根彎曲應(yīng)力云圖

圖18 太陽輪齒根彎曲應(yīng)力云圖

從齒根彎曲應(yīng)力云圖可以看出，嚙合過程中內(nèi)齒圈齒根彎曲應(yīng)力286.8MPa，太陽輪齒根彎曲應(yīng)力338.7 MPa，行星輪齒根彎曲應(yīng)力265MPa。

2.4 兩種仿真分析對比

按照標(biāo)準(zhǔn)漸開線圓柱直齒輪的強(qiáng)度校核方法，所得各個(gè)齒輪接觸應(yīng)力與齒根應(yīng)力，仿真結(jié)果與理論值對比如表2所示。

表2 仿真結(jié)果與理論結(jié)果對比表

由上表對比可知，理論分析結(jié)果與兩種仿真結(jié)果存在一定誤差，這是由于理論分析時(shí)把接觸看作線接觸，而在分析軟件中，模型采取面接觸，較理論分析可進(jìn)一步提高計(jì)算準(zhǔn)確性。無論是采用準(zhǔn)靜態(tài)分析還是顯示動(dòng)力分析都可以求出了各個(gè)嚙合輪齒處于不同嚙合位置的接觸壓力、應(yīng)力的大小及其分布。動(dòng)態(tài)分析可以在一次求解過程中，計(jì)算不同嚙合位置處的應(yīng)力及其變化趨勢。但是動(dòng)態(tài)分析時(shí)，齒輪嚙合狀態(tài)會(huì)不斷在單齒嚙合與雙齒嚙合交替變換，在嚙入嚙出時(shí)會(huì)存在嚙合沖擊，使得齒輪產(chǎn)生較大沖擊應(yīng)力。使用顯示動(dòng)態(tài)分析得到的輪齒應(yīng)力隨時(shí)間變化的仿真結(jié)果會(huì)更加接近實(shí)際齒輪嚙合過程。下圖所示分別為單齒嚙合時(shí)，準(zhǔn)靜態(tài)分析過程與顯示動(dòng)力分析過程中太陽輪應(yīng)力沿齒根方向的變化云圖。

圖19 準(zhǔn)靜態(tài)分析過程太陽輪接觸應(yīng)力沿齒根方向的變化云圖

在上述云圖中，可以看出靜態(tài)分析在3.5處應(yīng)力達(dá)到最大值，在4.5附近又出現(xiàn)較大應(yīng)力處，而動(dòng)力分析中嚙合在4.5處出現(xiàn)應(yīng)力峰值，而齒輪在嚙合過程中，主動(dòng)齒的應(yīng)力由齒頂向齒根方向擴(kuò)散，在節(jié)圓處達(dá)到最大值。

3 結(jié)論

本文主要對比了兩種仿真分析方法對于行星傳動(dòng)動(dòng)態(tài)嚙合輪齒的應(yīng)力分布規(guī)律，探究了齒輪在不同嚙合位置時(shí)齒面的接觸應(yīng)力、齒根應(yīng)力的變化等，結(jié)論與理論分析基本吻合。

準(zhǔn)靜態(tài)通用分析能夠模擬行星輪系動(dòng)態(tài)分析，建立較為平穩(wěn)的接觸關(guān)系，在分析中計(jì)算稍許簡便。且仿真結(jié)果與理論值誤差較小。顯示動(dòng)力分析能夠高保真地模擬出齒輪實(shí)際嚙合過程，對于進(jìn)一步輪系的動(dòng)態(tài)特性研究有著深刻意義。而在實(shí)際生產(chǎn)生活中，結(jié)合兩種仿真方法與理論分析，則將對輪系的優(yōu)化以及系統(tǒng)可靠性研究提供重要保證。