代數與幾何齊飛
——破解高考解析幾何中的定值、定點問題

夏 錦

(浙江省余姚市第四中學 315400)

浙江省高考數學文理合卷之后，采取“放低起點，減緩坡度，增加層次”的命題策略，體現“育人與選拔兼顧，區分與導向兼顧”的命題策略，彰顯“文科的韻味，理科的深度”的命題特色.而對于解析幾何中定值與定點問題則是高考題中的寵兒之一，由于這類題型它在解題之前不知道定值與定點的結果，對學生而言解題有相當大的難度.解決這類問題時，要善于在動點的“變”中尋求定值的“不變”性，常用特殊探索法(特殊值、特殊位置、特殊圖形等)先確定出定值與定點，再轉化為有方向有目標的一般性證明題，從而達到解決問題的方法.

一、定值問題

(1)求雙曲線C的方程；

(2)設直線l是圓O:x2+y2=2上動點P(x0,y0)(x0,y0≠0)處的切線，l與雙曲線C交于不同的兩點A,B，證明∠AOB的大小為定值.

二、定點或三線共點問題

分析要證明線段AC的垂直平分線經過某一定點，只要求出該直線系，再證此直線系通過某定點.

三、存在型定值(或定點)

例3 (全國卷Ⅲ) 設A(x1,y1),B(x2,y2)兩點在拋物線y=2x2上，l是AB的垂直平分線，(Ⅰ)當且僅當x1+x2取何值時，直線l經過拋物線的焦點F？證明你的結論.

四、定曲線

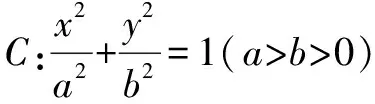
(1)求橢圓C的方程；

由于A(x1,y1),B(x2,y2)在橢圓C上，將①，②分別代入C的方程x2+2y2=4,整理得

(x2+2y2-4)λ2-4(2x+y-2)λ+14=0③,

(x2+2y2-4)λ2+4(2x+y-2)λ+14=0④.

④-③得8(2x+y-2)λ=0.

∵λ≠0,∴2x+y-2=0,即點Q(x,y)總在定直線2x+y-2=0上.