2018年全國Ⅰ卷文科第18題分析

蘇藝偉

(福建省龍海第一中學新校區(qū) 363100)

一、試題

如圖1所示,在平行四邊形ABCM中,AB=AC=3,∠ACM=90°.以AC為折痕將△ACM折起,使點M到達點D的位置,且AB⊥DA.

(1)證明平面ACD⊥平面ABC.

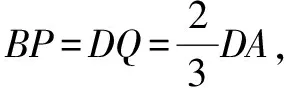
二、試題分析

本題是2018年全國Ⅰ卷文科第18題.從考查內容上看,主要考查立體幾何中常見的翻折問題,涉及到垂直的證明以及求三棱錐體積問題.從難易程度上看,試題分為兩步,梯度明顯,既可以讓不同的考生都有所收獲,還可以區(qū)分出不同層次的考生;從命題立意角度上看,主要考查空間想象能力,運算求解能力,推理論證能力.由于本省文科生沒有學習用建系法求解空間幾何問題,因此本道試題必須采用傳統(tǒng)的綜合法求解,所以說本題是考查學生是否掌握立體幾何基本功的一道好題.

1.對第一步分析

第一步要證明面面垂直,根據課本中面面垂直的判定定理,不難想到首先證明線面垂直,因此考慮證明AB⊥面ACD,借助線面垂直的判定定理進行證明.

證明:由AB⊥AC,AB⊥DA,AC∩AD=A,得AB⊥面ACD.又AB?面ABC,所以平面ACD⊥平面ABC.

不難看出,本小步主要考查學生是否正確掌握空間中點,線,面位置關系的判斷與證明.尤其是線面垂直判定定理,面面垂直判定定理的應用.這其中也滲透了轉化與化歸的數學思想方法.除了上述證明思路,其實還可以有如下的證明方法:

顯然DB2=DC2+BC2,因此DC⊥CB.由DC⊥CA,DC⊥CB,CA∩CB=C,得DC⊥面ABC.又DC?面ACD,所以平面ACD⊥平面ABC.

這個思路抓住翻折過程中的不變量,結合條件AB⊥DA,運用勾股定理巧妙求出線段長以及得到垂直關系,更能體現出此類翻折問題的本質以及命題者命制本道試題的初衷.

2.對第二步分析

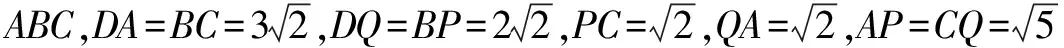
方法1:如圖2所示,作QE∥DC,交AC于E,因為DC⊥面ABC,所以QE⊥面ABC.因此頂點Q到底面ABP的距離即為QE=1.

方法2: 如圖2所示,作QE⊥AC,交AC于E,則QE∥DC,所以QE⊥面ABC.因此頂點Q到底面ABP的距離即為QE=1.

方法3: 如圖2所示,作QE⊥面ABC,因為DC⊥面ABC,所以QE∥DC,又DC⊥AC,

所以點E在AC上,因此頂點Q到底面ABP的距離即為QE=1.

方法4: 如圖3所示,作QE∥AC,交DC于E,則QE∥面ABP,所以頂點Q到底面ABP的距離即為點E到底面ABP的距離,即為EC=1,因此頂點Q到底面ABP的距離即為1.

上述四種方法其實本質是一樣的,都是在圖形中作出(找出)三棱錐Q-ABP的高,然后利用錐體的體積公式即可順利求解.可否不用作出高直接利用錐體的體積公式求解呢?

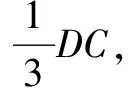
除了上述幾種解決方法,還可以運用分割法的思想來進行求解.

方法9:如圖4所示,作PN∥AB,交AC于N.由于AB⊥面ACD,所以PN⊥面ACD.

上述兩種方法是運用割補法中的分割法來求三棱錐Q-ABP的體積,雖然有些繁瑣,但是能夠很好地鍛煉學生的思維能力,計算能力,轉化能力,值得提倡.

3.閱卷過程中發(fā)現的錯誤

(1)第一步錯誤的地方有以下幾點：

①部分考生沒有正確寫出兩對垂直.

②部分考生只寫一對垂直就得到線面垂直

③部分考生由兩對垂直直接得到面面垂直.

④部分考生邏輯思維混亂,拼湊得到結論.

⑤書寫不規(guī)范,如把∩寫成∪,把面ACD⊥平面ABC寫成△ACD⊥△ABC,把?寫成∈.

(2)第二步錯誤的地方有以下幾點:

①不懂得求出頂點Q到底面ABP的距離.

②求出頂點Q到底面ABP的距離為2.

三、教學啟示

通過對題目的分析以及改卷過程中發(fā)現的錯誤,我們認為對立體幾何教學應注重以下幾方面.

1.立體幾何的教學首先要注重基礎,講透基本概念,基本定理

立體幾何是研究現實世界中物體形狀,大小與位置關系的數學學科,通過直觀感知,操作確認是學習這一知識的最好方法,因此教師在教學時要充分利用教學模型,引導學生真切,直觀,具體地觀察,感知,探究幾何教學模型中空間點,線,面之間的位置關系,利用多種形式表征結構關系,這樣學生更易于形成立體幾何的認知和學習習慣,掌握立體幾何的基本概念,基本定理,發(fā)展學生的空間想象能力,推理論證能力,提高圖形語言,文字語言,符號語言的轉化能力.

立體幾何教學的根本目的在于培養(yǎng)學生的數學核心素養(yǎng),其中關鍵在于提高學生的空間想象力,增強空間感知能力.為了實現這個目標,我們需要在直觀想象的基礎上培養(yǎng)學生的理性推理論證能力,理性的推理論證可以讓學生更能清晰地把握空間幾何體的空間位置,是學生建立科學空間觀必不可少的思維歷程.因此,在教學中,我們要幫助學生架構科學判斷空間位置的一整套推理論證的思維圖式.所謂思維圖式,即主體在遇到同屬性的問題時能及時作出相應思維的過程.在立體幾何模塊中具有非常多的思維圖式,例如空間線線角,線面角,二面角的求作;空間平行位置關系的判斷,空間垂直位置的判斷等等.對于這些問題,我們要讓學生建立正確而順暢的思維鏈,即一遇到什么問題,我們要順利地作出與問題相匹配的完整思維和動作,直至解決問題.

2.立體幾何的教學要注重幾何法(綜合法)

利用空間向量解決立體幾何問題弱化了立體幾何的教育價值,因為空間向量解決立體幾何問題更多是算法程序化的操作,少有對立體幾何圖形中點,線,面之間結構關系的分析,思考,不利于培養(yǎng)學生的空間想象能力.因此在立體幾何的教學中一定要注重幾何法(綜合法).

新考綱明確規(guī)定刪減幾何證明選講之后,高考命題調整考查方向,重在數學學科核心素養(yǎng)的考查,于是立體幾何試題就成了搭載考查平面幾何知識的載體和平臺,綜合考查能力陡然上升,學生的二維,三維空間思維得到很好的訓練.平面幾何知識滲透到立體幾何中后,解題思路和難度徒然增大,學生在二維和三維間思維中不斷轉換,容易形成思維混亂,知識斷層,思維鏈受阻,加上計算要求較高,就越發(fā)凸顯學生的某一方面能力的嚴重不足,這就要求在平時的復習備考中,各種能力的訓練不能馬虎,要有針對性,有的放矢,知識的專項訓練和綜合提升兩方面都要抓,都必須落到實處.