利用導函數性質證明數列不等式問題
2019-03-27 06:00:34耿玉明
數理化解題研究 2019年7期
耿玉明
(廣東省深圳市寶安中學 518101)
一、利用參數取值范圍的臨界值創設原型不等式
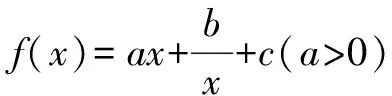
(1)用a表示出b,c;
(2)若f(x)≥lnx在[1,+)上恒成立,求a的取值范圍;
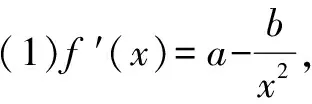
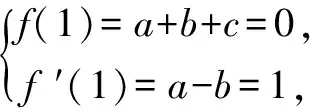
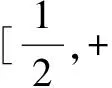
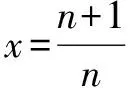
思維特點先根據參數a的取值范圍,取其臨界值創設原型不等式,再通過對x賦值證明數列不等式.
二、 利用函數單調性結論創設原型不等式
例2 已知函數f(x)=2aln(1+x)-x(a>0).
(1)求f(x)的單調區間;
解(1)可求f(x)的單調遞增區間為(-1,2a-1),單調遞減區間為(2a-1,+)(略)
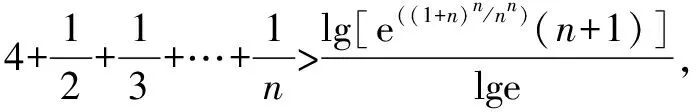
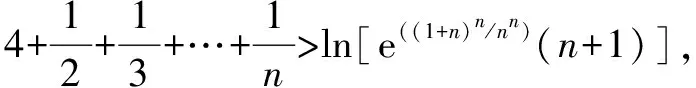
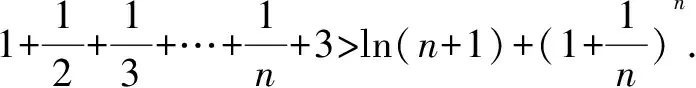
∴x∈(0,+)時,f(x) 思維特點先根據所求的單調區間,利用函數單調性在某一特定區間上創設原型不等式,再通過對x賦值證明數列不等式. 例3 已知函數f(x)=e1-x及g(x)=ln(3-x). (1)求函數f(x)與g(x)的公切線方程; (2)根據(1)結論,并由圖可知ln(3-x)≤-x+2≤e1-x對于x∈R恒成立 思維特點先根據所求函數f(x)的切線方程,并借助于函數的凸凹性創設在某一區間上的原型不等式,再通過對x賦值證明數列不等式.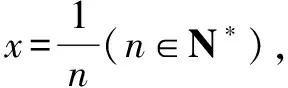
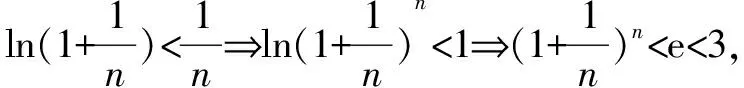
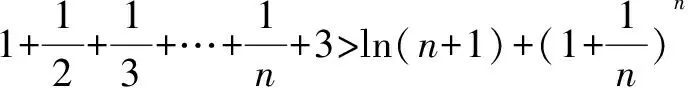
三、 利用函數的切線方程創設原型不等式
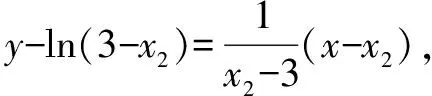
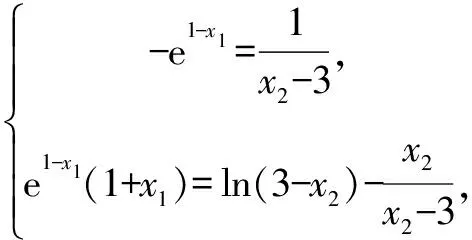
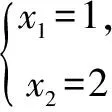
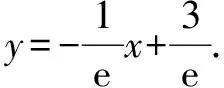
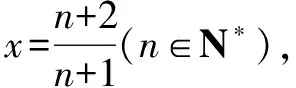
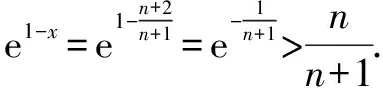
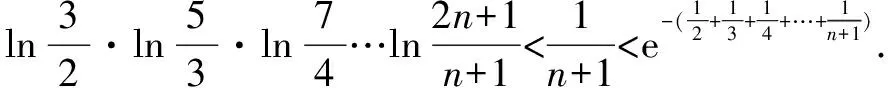
猜你喜歡
小哥白尼(野生動物)(2022年6期)2022-08-17 08:05:28
小哥白尼(野生動物)(2022年4期)2022-07-16 03:37:32
中等數學(2022年2期)2022-06-05 07:10:50
小哥白尼(野生動物)(2022年2期)2022-06-01 06:21:20
小哥白尼(野生動物)(2022年1期)2022-04-26 14:01:18
作文成功之路·小學版(2020年6期)2020-07-27 01:48:22
小學生學習指導(低年級)(2020年6期)2020-07-25 02:31:36
甘肅教育(2020年8期)2020-06-11 06:10:20
福建基礎教育研究(2019年11期)2019-05-28 07:25:10
小學生學習指導(低年級)(2018年9期)2018-09-26 05:59:44

