特殊化策略在初中數(shù)學解題中的應(yīng)用

王朝梅

(安徽省合肥市50中學南校 230000)

目前，初中數(shù)學問題在解答過程中普遍具有特殊性，故而教師在進行數(shù)學習題解答的過程中，需要加強對于特殊化策略的運用.本文基于此，著重論述特殊化策略在數(shù)學習題中的運用，希望由此實現(xiàn)數(shù)學教學質(zhì)量以及效率的提升，促進各項教學效果的取得.

一、特殊化策略運用與思維嚴謹培養(yǎng)

我國中學階段開設(shè)數(shù)學科目的主要原因，在于培養(yǎng)學生的思維能力.一般而言，學生在進行數(shù)學習題解答的過程中需要進一步保障答題的嚴謹性以及周密性.數(shù)學習題在解答分析作業(yè)時普遍具有思維嚴謹性，且需要遵循一定的邏輯規(guī)律.基于此，教師引導(dǎo)學生明確解題思路，并巧借特殊化方法，從特殊最佳情形入手探究和分析數(shù)學問題，實現(xiàn)學生解題思路的開拓，并進一步培養(yǎng)學的邏輯思維能力.

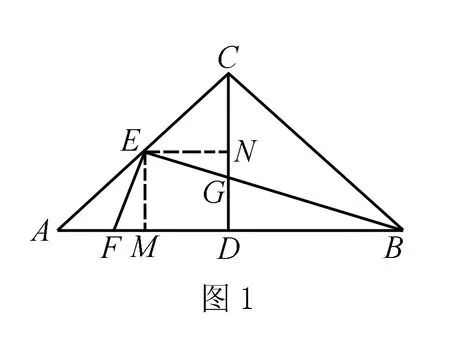
例1 “如圖1所示，在Rt△ABC中，∠ACB=90°,CD⊥AB,垂足為D，點E在AC上，BE交CD于點G，EF⊥BE交AB于點F，若AC=mBC，CE=nEA(m，n為實數(shù))，請?zhí)骄烤€段EF與EG的數(shù)量關(guān)系.”

對于初中的學生而言，這一道題目具有一定的難度，學生如果借助一般的幾何分析方法進行解答時，往往會陷入思維僵局中，但是學生如果采取特殊化的策略進行解答，其往往能夠?qū)崿F(xiàn)問題的突破，促進問題解答效率以及質(zhì)量的提升.

二、特殊化方法與思維批判性培養(yǎng)

所謂的數(shù)學思維批判性，指的是學生在數(shù)學問題解答時能夠具備獨立思考的能力，同時能夠科學地進行數(shù)學問題的分析以及解答，并對材料中的論證論據(jù)提出質(zhì)疑.一般而言，特殊化方法的合理化運用，能夠進一步地培養(yǎng)學生判斷疑問的能力，從而進一步引導(dǎo)學生對于各類論據(jù)特殊情況的分析.目前，教師在進行數(shù)學題解答分析教學時，可以巧妙地利用各類特殊化方法，引導(dǎo)學生對于各特殊情況的分析以及驗證，從而確保其能夠?qū)ψ约旱慕忸}不足之處進行總結(jié)、認識，實現(xiàn)了自身的完善發(fā)展，可以在最大程度上帶動了其解題思維以及明辨是非能力的增長.

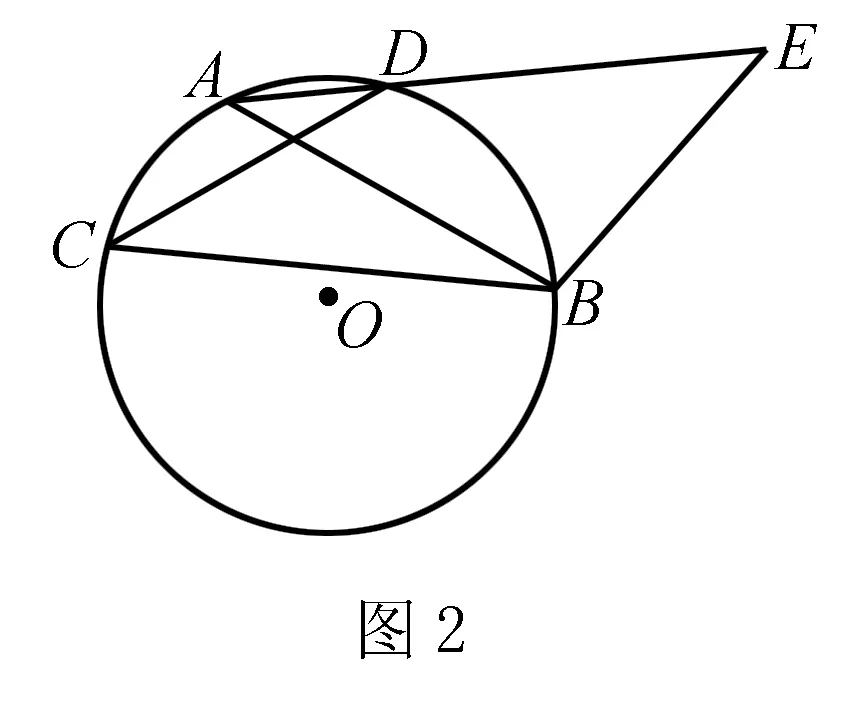
以數(shù)學題“有一組對邊和一組對角相等的四邊形是平行四邊形是否是真命題” 為例進行相關(guān)的分析.如圖2所示：在⊙O中作出兩條相交的等弦AB、CD，并將AD、BC進行連接，延長AD至E點，并使BE=AB.這一作圖之后能夠得到等腰三角形△ABE，而四邊形CDEB這就符合上述的命題假設(shè).在這一命題假設(shè)的影響下，我們可以得知∠C=∠E，而且線段CD與線段BE的長度相等.但事實上，如果四邊形CDBE并非平行四邊形，則上述的命題為假命題.

三、特殊化策略與思維靈活性培養(yǎng)

所謂的靈活性思維，指的是學生在數(shù)學問題分析以及解決的過程中，能夠進一步打破傳統(tǒng)的思維模式，并借助不同的視角、層面進行問題的思考以及發(fā)掘，從而明確問題的解決方法.目前，我國的中學生在數(shù)學學習的過程中，普遍依賴教師，進而導(dǎo)致其在問題分析時缺乏必要且科學的主動性，最終形成了思維僵化的問題，無法做到舉一反三.

而特殊化策略的運用，則能夠?qū)崿F(xiàn)學生思考問題的角度轉(zhuǎn)變，確保其在問題的分析過程中能多層次探求特殊情形，實現(xiàn)其思維靈活性、廣闊性的增強，實現(xiàn)自身思維能力的提升，從而為數(shù)學教學目標的實現(xiàn)奠定基礎(chǔ)，促進更高效益的取得.

例2a、b、c是不全等的任意實數(shù)，若c=a2-bc，y=b2-ac，z=c2-ab，則x、y( ).

A.都不小于0 B.都大于0

C.至少有一個大于0 D.至少有一個小于0

在進行該類問題解答的過程中，學生往往進行式子的轉(zhuǎn)換，進而忽視了對于特殊數(shù)值取值的方法進行解答.在這道題目中，學生能夠發(fā)揮其靈活性，將a設(shè)定為0，b為1，c為-1進行該題的解答.在這樣的狀況下，學生可以排除選項D，隨后學生再設(shè)定a=0，b=c=1，則x=-1，y=z=1，又可以排除A、B，所以答案選擇C.

隨著相關(guān)教學理念的轉(zhuǎn)變以及教學方法的運用，我國的特殊化策略必將能夠融入到數(shù)學教學過程中去，并由此實現(xiàn)教學質(zhì)量的提升，確保初中數(shù)學教學工作符合時代發(fā)展的需要，促進學生的全方位進步，謀求更高的教學效益.