非淹沒剛性植被影響下孤立波在岸灘上的爬高

姚 宇,唐夢君,唐政江,蔣昌波,3

(1.長沙理工大學水利工程學院,湖南 長沙 410114;2.河海大學海岸災害及防護教育部重點實驗室,江蘇 南京 210098;3.水沙科學與水災害防治湖南省重點實驗室,湖南 長沙 410114)

海嘯是由海底地震、火山爆發、海底滑坡或氣象變化產生的破壞性海浪,海嘯波與海岸相互作用后產生的海面爬高可能會給沿岸地區造成嚴重的洪澇災害。對2004年印度洋大海嘯的災后調查研究發現,沿岸生長的紅樹林類剛性植被能對海嘯波起到顯著的削弱作用[1-2],培植海岸植被認為是未來一種積極的海嘯防御措施。因此研究海嘯波與紅樹林類剛性植被的相互作用對海嘯災害的防治具有一定的指導意義。

由于海嘯波的首波與孤立波十分接近,因此學術界多采用孤立波來模擬海嘯波的首波[3]。物理模型試驗是研究孤立波與植被相互作用問題的主要手段之一,國內外學者在波浪水槽中對孤立波與平底海岸上剛性植被的相互作用問題進行了大量的研究工作[4-8],而關于孤立波與斜坡海岸上剛性植被的研究則相對較少。Irtem等[9-10]通過物理模型試驗,研究了孤立波在非淹沒剛性植被存在條件下的斜坡上的爬高問題,但未考慮岸灘坡度變化對剛性植被存在下孤立波爬高的影響。

植物的阻力系數一般難以直接測量[11],數值模型是獲取植被阻力系數的一種可行的方法。對于長波與植被相互作用的模擬,常用的數值模型有求解淺水波方程的模型[12],求解Boussinesq方程的模型[4-5]和直接求解Navier-Stokes方程的CFD方法[13]，其中Boussinesq方程兼顧計算精度和計算效率,得到了較為廣泛的應用。姚宇等[14]首次采用Boussinesq方程模擬了孤立波與斜坡上非淹沒剛性植被的相互作用,并通過添加拖曳力項對植被阻力進行描述,得出了拖曳力系數隨波高和植被密度的變化關系,但是尚未涉及不同斜坡坡度的情況。

本文擬在改進Yao等[10]物理模型試驗的基礎上,對非淹沒剛性植被影響下孤立波在不同斜坡上的傳播變形及爬高特征進行試驗,并采用校核后的Boussinesq數值模型與試驗結果進行對比驗證,研究結果可為通過培植近岸植被來防治海嘯災害的實踐活動提供參考。

圖1 物理模型布置(單位：m)

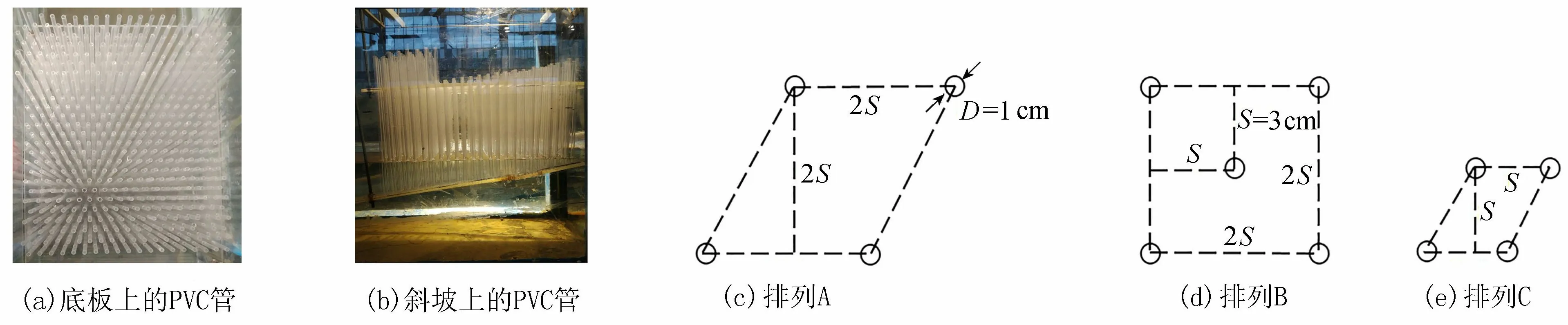
圖2 植被區域的排列方式

1 物理模型試驗

長沙理工大學水利實驗中心波浪水槽長45 m、寬0.5 m、高0.8 m,水槽左端配備有一臺活塞式造波機,可產生包括孤立波在內的多種波況。物理模型在水槽中的布置如圖1所示，岸灘斜坡采用PVC板來模擬,坡腳設置在距造波機17 m處,在距坡腳水平距離1.16 m的斜坡上布置有長0.6 m、寬與槽寬一致的植被區,區內單株剛性植物采用直徑為1 cm,高度為30 cm的PVC圓管來模擬。將植株按照一定的排列方式垂直固定在預留孔洞的PVC板上(圖2(a)),固定板懸掛于斜坡上方,植株的下端與斜坡接觸并用玻璃膠固結(圖2(b))。

植被排列的密度可采用固體體積分數φ=Vs/V進行計算,其中V為控制體體積;Vs為控制體中植被固體所占的體積。采用圖2(c)所示的3種植株交錯布置的方案,分別命名為排列A、排列B和排列C,密度分別為:φA=0.087、φB=0.109、φC=0.196。

設置坡度分別為1∶6、1∶8、1∶10的3種岸灘坡度,在改變坡度的過程中植被位置保持不變。測試水深固定為30 cm,入射波波高分別設置為2 cm、4 cm、6 cm、8 cm和10 cm,所有工況下植株頂部均處于非淹沒狀態。使用4個超聲波浪高儀S1～S4測量自由液面的變化;采用CCD高速相機記錄孤立波的爬坡過程,孤立波的爬高通過分析圖像中波浪在標有刻度的斜面上的最大上爬位置而得。

2 數值模型模擬

采用一維高階強非線性Boussinesq方程來模擬波浪沿礁的傳播變形過程[15]。由于植株模型呈圓柱狀,植被的阻力可采用拖曳力來描述。擬定x軸的正向為波浪傳播方向,t為時間,仿照姚宇等[14]通過添加拖曳力項來模擬植被阻力,改進后的一維Boussinesq方程為

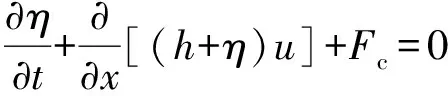
(1)

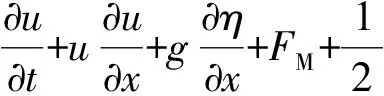
(2)

式中:η為自由液面的位移;h為平均水深;D為總水深,D=h+η；u為高程-za處水平方向速度(za=0.531h);up為植被區內沿x方向的孔隙流速;ρ為水的密度;dt為植株直徑;Nt為單位面積內的植株數;Cd為植被拖曳力系數;τb為底床摩擦力;FC和FM為淺水波方程的Boussinesq校正項。

up與u關系通過下式確定:

(3)

式中:θ為斜坡角度。

τb可由曼寧系數n求得:

(4)

式中：g為重力加速度。

此外,由于沿水深積分的Boussinesq模型不能描述自由表面的翻轉和詳細的波浪破碎過程,因此需要添加半理論半經驗的破碎波模型來模擬波浪破碎所造成的能量損失,以求更好地模擬波浪傳播變形過程。破碎波模型采用Kennedy等[16]提出的渦黏模型。該模型中需設置4個經驗參數,參照Lynett等[17]的建議取δ=6.5,α1=0.65,α2=0.08,α3=8.0。

3 模型試驗與數值模擬結果對比分析

3.1 底床摩擦因數和植被拖曳力系數的校核

由于波浪在斜坡岸灘上的爬高受到底床摩擦的影響,首先必須對式(4)中的摩擦因數進行校核。校核的原則是選取有代表性的工況首先調整入射波高使S1測點的波高H1與試驗測量一致,隨后調整曼寧系數n使計算的S2～S4位置波高H2～H4以及岸灘爬高R與試驗測量的符合程度達到全局最優,經校核得到n=0.003。圖3比較了坡度為1∶6且無植被時H2～H4以及R間的實測和模擬結果,總體而言兩者符合程度較好。

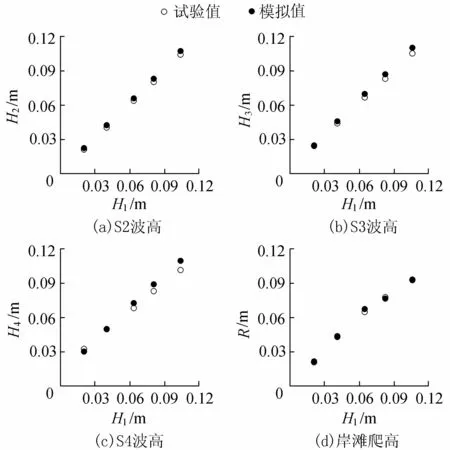
圖3 無植被時波高和爬高的試驗與數值模擬結果對比

除植被區外采用校核的摩擦因數,植被拖曳力系數的校核通過調整式(2)中的Cd值確定,校核的原則是使計算的透射波高H4與試驗結果符合程度達到最優。考慮到對波高的測量較對爬高的測量更為精確,選用H4而不是R作為校核標準。各測試波高下校核得到的拖曳力系數Cd的平均值如表1所示。由表1可以看出,Cd值隨著植被密度的增加而增加,隨斜坡坡度的增大而減小。Cd的取值范圍在1.5～3.5之間,與Huang等[4]孤立波與平底植物相互作用的范圍1.5～2.5和Iimura等[5]孤立波與斜坡植物相互作用的范圍0.6～2.2類似,一定的差異與植被密度不同及坡度不同有關。

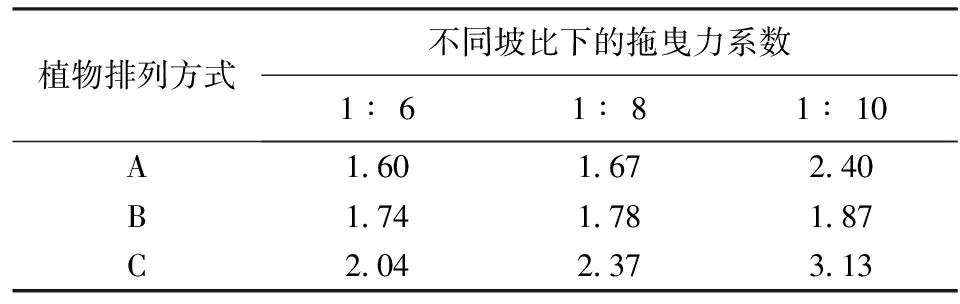
表1 不同坡度時的平均拖曳力系數

3.2 自由液面時間序列的比較分析

圖4 不同測點試驗和數值模擬的η過程對比

圖4為波高6 cm的入射波與植被排列B作用時,不同岸灘坡度S1～S4位置測量和模擬的自由液面η的歷時曲線對比。圖4表明:S1～S3位置測量的自由液面均存在3個明顯的峰值,首先出現的為入射波波峰,隨后出現的為植被區反射造成的反射波波峰,最后為岸灘反射造成的波峰,3個波峰在靠近遠海側(S1)且岸灘坡度最小時(1∶10)分開得最為明顯;S4處僅存在透射波波峰和岸灘反射造成的波峰,這種反射波也是在岸灘坡度1∶10的時候更加明顯。同時在反射波后面緊接著出現一個明顯的水位降低,這是波浪回退的階段產生了水躍現象造成。當岸灘坡度為1∶6時,S4位置岸灘高程位于靜水位以上,故透射波傳播到此時已接近爬坡的最高點,S4處除了透射波的主峰外,并無岸灘反射波和回落水躍現象。對于數值模擬而言,所采用的Boussinesq模型對于3種岸灘坡度的入射波峰的模擬較為準確,僅在反射波的模擬方面略有差異;此外沿水深積分的Boussinesq方程無法捕捉到S4處的回落水躍存在。

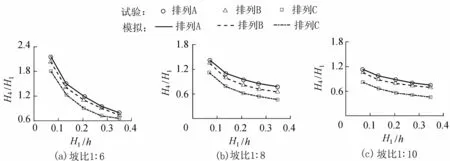
圖5 無量綱透射波高H4/H1隨H1/h的變化

3.3 透射波高的比較分析

圖5為不同植被密度和岸灘坡度影響下,無量綱透射波高H4/H1隨無量綱入射波高H1/h的變化規律。圖5表明:對于所有植被排列和岸灘坡度而言,H4/H1隨H1/h的增大而減小;對不同密度的植被排列進行對比發現,當入射波高一定時,透射波高隨植被密度的減小而增大,這與表1中密度越小阻力系數越小的結論相對應;通過對比不同岸灘坡度發現,當植被排列相同時,岸灘坡度越大,透射波高亦越大,大部分工況的H4/H1>1,即出現透射波高大于入射波高的情況,這主要是由于坡度較陡時,波浪與斜坡上植被相互作用時過水面積減小導致阻水效應減小,且小于斜坡上由于波浪淺化作用造成的波高變陡。同時,圖5中所有工況下的實測和模擬的透射波高吻合度均較好。

3.4 岸灘爬高的比較分析

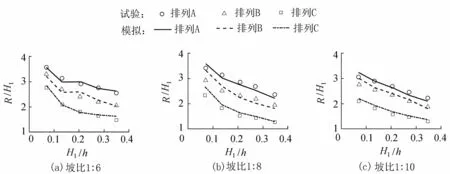
圖6 無量綱透射波高R/H1隨H1/h的變化

圖6為不同植被密度和不同岸灘坡度影響下,無量綱岸灘爬高R/H1隨S1處無量綱入射波高H1/h的變化情況規律。圖6表明:H1/h越小,R/H1越大;對比不同密度的植被排列表明,當入射波高和斜坡坡度不變時,岸灘爬高隨著植被密度的減小而增大,這與3.3節的結論一致,均是由于植物密度的增大加強了植物的阻水效應造成[14],這也與表1中拖曳力系數隨著植被密度的增大而增大的現象一致。當對比不同岸灘坡度的爬高發現,雖然S4處透射波高在坡度陡時較大(圖5),相同的植被排列在相同的入射波作用下的無量綱爬高并無顯著差異,這是因為陡坡的存在抑制了透射波在岸灘上的進一步上爬,造成不同岸灘坡度間的爬高值比較接近。總體而言,所采用的數值模型能較好地模擬植被區后岸灘上孤立波的爬高變化規律,對某些工況存在一定的誤差,可能是物理模型試驗中干濕分界線沿槽寬分布不均造成的測量誤差所致。

3.5 關于爬高的進一步討論

參照Synolakis[18]提出的預測平直海岸的孤立波爬高關系式,經回歸分析得無量綱波浪爬高隨無量綱入射波高、植被密度和岸灘坡度3個因素變化的冪函數型經驗關系為

(5)

式中:β為試驗中的岸灘坡度。式(5)的擬合情況如圖7所示,擬合精度為r2=0.98,表明式(5)可以較好地預測不同坡度的岸灘斜坡上的孤立波爬高。

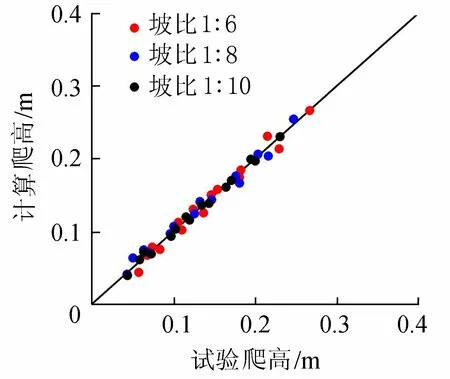
圖7 實測與式(5)計算的岸灘爬高對比

對式(5)進行了顯著性檢驗以及對3個自變量進行了F檢驗,顯著性分析及自變量的F值的檢驗結果如表2所示。通過3個影響因子對相對爬高的顯著性檢驗分析得到3個自變量的顯著性值均小于0.05,因此它們對爬高均存在顯著影響。

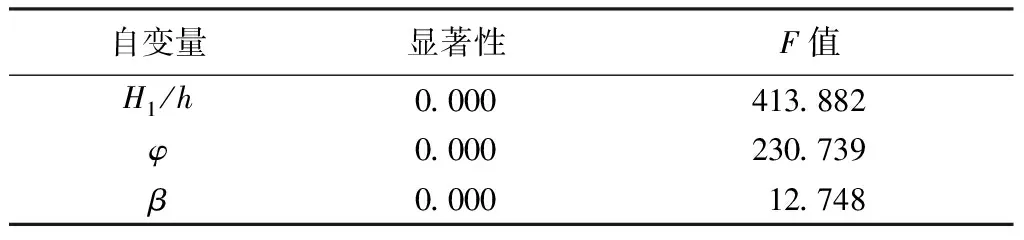
表2 自變量的顯著性檢驗(置信水平為0.005)

4 結 論

a. 無量綱透射波高和無量綱岸灘爬高隨著無量綱入射波高的增大而減小,同時它們也隨著植被密度的增大而減小;當岸灘坡度增大時,無量綱透射波高增大而無量綱的爬高卻無顯著差異。

b. 通過添加拖曳力項改進了的Bounssinesq方程能較好地模擬孤立波與不同坡度上的非淹沒剛性植被的相互作用;由數值模型所得拖曳力系數隨植被密度的增大而增大,隨坡度增大而減小。

c. 根據回歸分析得出了岸灘爬高與相對入射波高,植被密度和岸灘坡度的冪函數型經驗關系式,實測數據的相關分析與顯著性檢驗均顯示該關系式具有較高的精確度。