SWMM模型河道及明滿流模擬能力分析研究

范玉燕， 汪誠文， 喻海軍

(1.清華大學 環境學院， 北京 100084； 2.中國水利水電科學研究院， 北京 100038； 3.水利部防洪抗旱減災工程技術研究中心， 北京100038)

1 研究背景

城市暴雨內澇是當前城市水文學研究的熱點問題，城市雨洪模型是必不可少的研究工具之一[1]。在眾多的城市雨洪模型當中，SWMM(Storm Water Management Model)模型[2]是使用最為廣泛的模型之一，其一系列建模理念對后續其它城市雨洪模型產生深遠的影響[3]，并被廣泛地應用于世界各地不同城市地區的暴雨洪水管理、排水系統分析和設計、低影響開發模擬評估、城市地區非點源污染評估等方面的問題[4-6]。黃國如等[7]和韓璐遙等[8]分別針對深圳民治河流域和龍巖市中心城區的不同LID措施和方案，采用SWMM模型對雨洪控制效果進行了分析研究。朱呈浩等[9]基于SWMM模型對西安市灃西新城區洪澇過程進行了模擬分析。由于模型代碼完全免費和開源，將SWMM模型與GIS技術或者其它模型進行集成耦合是研究城市雨洪問題的重要技術路線[10-13]。經過近50年的發展，SWMM模型從功能和算法上已經相對比較成熟，但在城區河道處理、模型穩定性等部分問題還有待深入研究。

河道作為城市排水系統的重要組成部分，是暴雨內澇模擬分析中不可回避的問題，河道水流的模擬精度對城市排水模型整體的精度有著較大的影響。在構建城市排水模型時，考慮到構建管網和河網耦合模型的復雜性，部分研究者往往會直接采用SWMM模型同時模擬城區河網和排水管道[7, 14]。SWMM模型可以處理壓力流和明渠流，從理論上講是具備模擬城區河道能力的，但在SWMM模型中模擬河道時，需要將一條河道劃分成若干個小的河段，每個河段類似于一根管道，只可以設置一個斷面形狀，通過兩端節點高程來反映河道比降。河道斷面(如河寬和河深)一般是變化的，這一點與排水管道截面形狀一般沿程不變的情形完全不同，如果一個河段只能設置一個截面形狀，相當于假定這一河段形狀沿程不變，與實際情況有所差別，而傳統河網模型，一般是一個河段用上下游兩個斷面來反映河道地形變化。SWMM模型能否用于城區河道模擬以及采用類似管道的方式來模擬河道產生的誤差為多少有必要進行深入研究。

除上述問題之外，SWMM模型一維水動力學模塊基于“LINK-NODE”的思想，采用顯式有限差分格式離散求解一維圣維南方程組，即在LINK(管道)中滿足動量方程，在NODE(節點)中滿足連續方程[2]，這種數值處理方式從模型穩定性的角度來說是有所欠缺的，特別是在處理明滿流這類復雜流態時尤為突出。城市排水系統中管道水流可能是滿流(壓力流)，也可能是明流(明渠流)，兩種流態可能會交替出現或者共存，這種明流和滿流兩種不同流態共存或者交替出現的水流稱之為明滿流[15]。從模型模擬能力方面來看，對排水系統中明滿流的模擬是排水管網模型必須具備的能力，也是重要的研究方向之一，目前對SWMM模型模擬明滿流的能力，特別是建模策略等方面研究還相對較少。

本文以SWMM模型為研究對象，重點分析和驗證了SWMM模型水動力學模塊處理城區不規則斷面河道和處理管道明滿流方面的能力，以期為實際應用SWMM模型提供科學支撐和依據。

2 SWMM模型簡介

SWMM模型是在美國環境保護署的資助下，由美國3家知名科研機構和公司聯合研發的城市雨洪管理模型，最新版本(5.1)已經具備水文、水力和水質等過程的模擬分析功能。

2.1 模型結構

SWMM模型總體上可以分為圖形界面引擎和模型計算引擎兩大主要模塊，兩個模塊之間通過文件系統進行數據交互(如圖1所示)。圖形界面引擎主要功能是進行模型要素(管網、泵、閘、堰等)的圖形編輯、屬性輸入和參數設置，并生成相應格式的輸入文件，供計算引擎調用。計算引擎調用輸入文件進行計算，主要包括地表產匯流、管網匯流和水質模擬等過程，計算完成后生成相應格式的結果文件和報告文件(即統計分析文件)，可在圖形界面上進行多種形式的展示和查詢。

2.2 模型功能

SWMM模型在降雨產匯流方面的功能相對比較完善，能夠模擬計算城市地區降雨、地表蒸發、積雪和融雪、土壤動態下滲、坡面匯流、地下水交互、各類LID設施產流等在內的多種水文過程。在管網匯流方面，SWMM模型可以提供恒定流、運動波和動力波等多種數值方法供用戶選擇，能夠模擬計算雨水徑流或其它形式外部入流在排水管網、河道、蓄水單元以及排水建筑物等排水系統中的傳輸和流動過程，另外模型還提供了比較完善和靈活的排水建筑物(泵站、堰、分流器等)的調度和控制功能。除了各類水文和水力過程的模擬之外，SWMM模型還提供了多種數學方法計算城市區域污染物累積沖刷和污染物在排水系統中輸運降解等水質過程。SWMM模型產匯流主要計算流程如圖2所示。

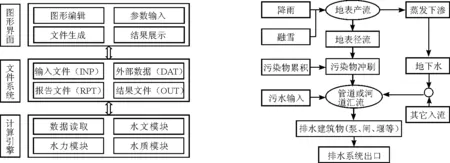
圖1 SWMM模型結構示意圖 圖2 SWMM模型計算流程

2.3 模型原理

(1)產匯流計算。SWMM模型在計算地表產流量時，一般需要將計算區域劃分成若干個子匯水區(或子流域)，每個子匯水區根據地表是否存在洼蓄損失和土壤下滲作用按不同比例劃分為透水區、無洼蓄不透水區和有洼蓄不透水區等3個內部組成部分，各部分均概化成一個非線性水庫單獨進行產流計算，子匯水區總的出流量等于3個內部子區域出流量之和。非線性水庫的入流項主要包括降雨和來自其他子匯水區的出流量，損失和流出項包括地表蒸散發、土壤下滲和出流量。非線性水庫的實時水深根據子匯水區的流入流出和損失項之間的水量平衡計算得出。子匯水區的最大洼蓄量相當于非線性水庫的死庫容，只有當水庫水深超過洼蓄深度時才會產生地表徑流，出流量的大小通過曼寧公式計算得出：

(1)

式中：Q為出流量，m3/s；W為子匯水區的概化寬度，m；S為子匯水區的坡度；n為曼寧粗率系數。

(2)一維管網。SWMM模型中一維排水管網模型控制方程分為連續方程和動量方程，分別如式(2)和式(3)所示。

(2)

(3)

式中：Q為管段流量，m3/s；A為管段過水斷面面積，m2；t為時間，s；x為距離，m；H為水頭，m；g為重力加速度，取9.8 m/s2；Sf為摩阻項，可以采用曼寧公式求得：

(4)

式中：K=gn2，n為管道的曼寧系數；R為過水斷面的水力半徑，m；V為斷面平均流速，m/s。

3 河道模擬能力驗證

為了對SWMM模型中以管道的方式考慮城區河道造成的模擬誤差進行評估，以證明SWMM模型是否能夠應用于城區河道的模擬分析計算，采用SWMM模型模擬計算了一條斷面尺寸沿程變化的河道，并將模擬計算結果與采用常規概化方式的MIKE11河網模型的計算結果進行對比。

3.1 算例

本次模擬計算案例采用的河道總長為3 km，由于城區河道一般是矩形或者梯形，本案例斷面形狀也統一采用對稱梯形斷面(如圖3所示)，梯形坡度比為2(圖3中h與a的比值)。如圖4中所示，在里程為0、1 000、2 000和3 000 m處，河道底寬(即圖3和圖4中w的取值)分別為30、40、40和60 m，河道底高程分別為4、2、1和0.5 m。

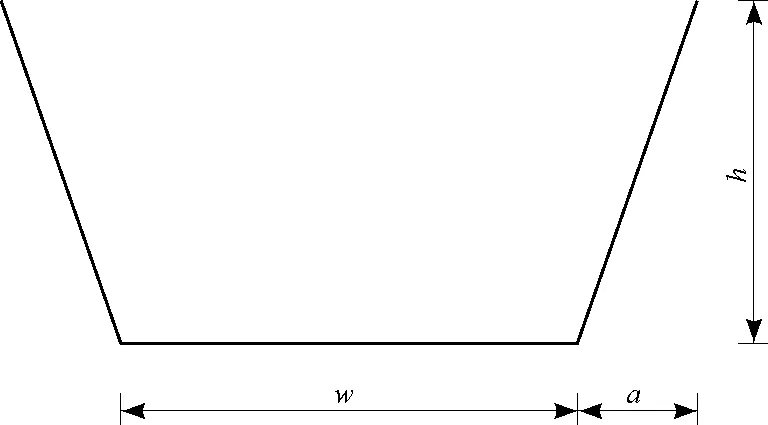
圖3 河道斷面示意圖

圖4 河道沿程底寬變化示意圖(單位：m)

3.2 結果分析

分別采用SWMM模型與MIKE11軟件構建了一維河道模型，模擬計算了不同入流流量和水位邊界條件下河道沿程的水位。在模型構建時，兩個模型均采用250 m的斷面間隔，其中SWMM模型中河段的形狀采用兩端處斷面形狀的平均，整條河道糙率系數均采用0.025。

圖5給出了不同量級的入流流量(Q=50，250和500 m3/s)和下游水位條件(H=1.8、2.6、3.0和5.0 m)下，SWMM模型和MIKE11軟件河道沿程水位計算結果的對比情況。從圖5可以看出，兩個模型的計算結果總體上非常接近，在里程1 500 m以內的斷面計算結果基本一致，下游水位差異略有增大，但水位差總體上均未超過15 cm，實際上如果將斷面進行適當加密，兩個模型計算結果差異將會進一步減少。從結果差異的原因來看，一部分可能是由于斷面概化方式導致的，另一部分可能是模型在下游邊界處理方式上不同造成的，但差別總體上控制在較小的范圍內。上述案例的計算結果表明采用SWMM模型中河道概化方式造成的誤差在可以接受的范圍內，SWMM模型可以用來模擬計算實際城區河道水流。

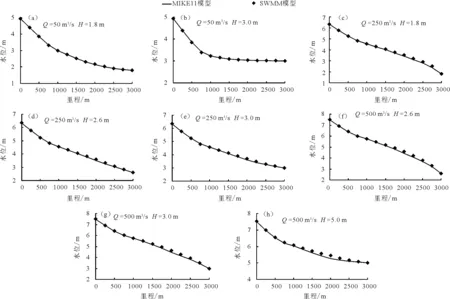
圖5 不同邊界條件下河道沿程水位對比圖

4 明滿流模擬能力驗證

為了對SWMM模型處理明滿流的能力進行檢驗，將SWMM模型應用于由Zhong Ji[16]提出的一個環狀算例，該算例被普遍應用于驗證模型處理明滿流的能力[17-18]。如圖6所示，該算例采用的排水管網系統由6根管道和6個節點組成，其中C2、C3和C4組成了一個封閉的環，各個管道的長度、管徑以及兩端的底高程均已在圖中標識，所有管道糙率統一采用0.01429。

在節點1和節點3處分別給定流量過程作為上邊界條件，節點5和節點6處分別給定水位過程作為下邊界條件，流量過程和水位過程如圖7所示。按圖7中給定的邊界條件，所有管道水流均從最初的全干狀態變為明渠流，隨著流量的不斷增大，管道中水流逐漸變為壓力流，最后當流量變小時，水流又會變回明渠流，也就是說本算例存在著明顯的明滿流交替過程，可以檢驗模型處理明渠流、壓力流和明滿流的能力。另外，由于下游水位邊界較高，在最初上游尚無來水時，C5和C6會出現逆流現象，因而還可以檢驗模型處理逆流的能力。

采用SWMM模型中動力波方法模擬計算了本算例，總的模擬時長為10 h，時間步長采用10 s，管道C2、C4、C5和C6中的流量過程計算結果如圖8所示。作為對比，圖8中也給出了文獻[16]中的模型計算值。從這些圖中可以看出，除局部有一些小的波動外，SWMM模型的計算結果與文獻中模型計算結果基本一致，表明SWMM模型能夠較好地處理明滿流的過渡，具備模擬明滿流的能力。

在上述的模擬計算中，所有管道(C1至C6)在建模時均被當作一根管道，相當于模型的空間步長為管道的長度，為了進一步評估SWMM模型處理明滿流的能力，在建模時，將每根管道中間位置設置一個虛擬的節點，再次進行了模擬計算，圖9給出了C2、C4、C5和C6管道中的流量過程。

圖6 算例管網示意圖(單位：m) 圖7 入流和出流邊界條件

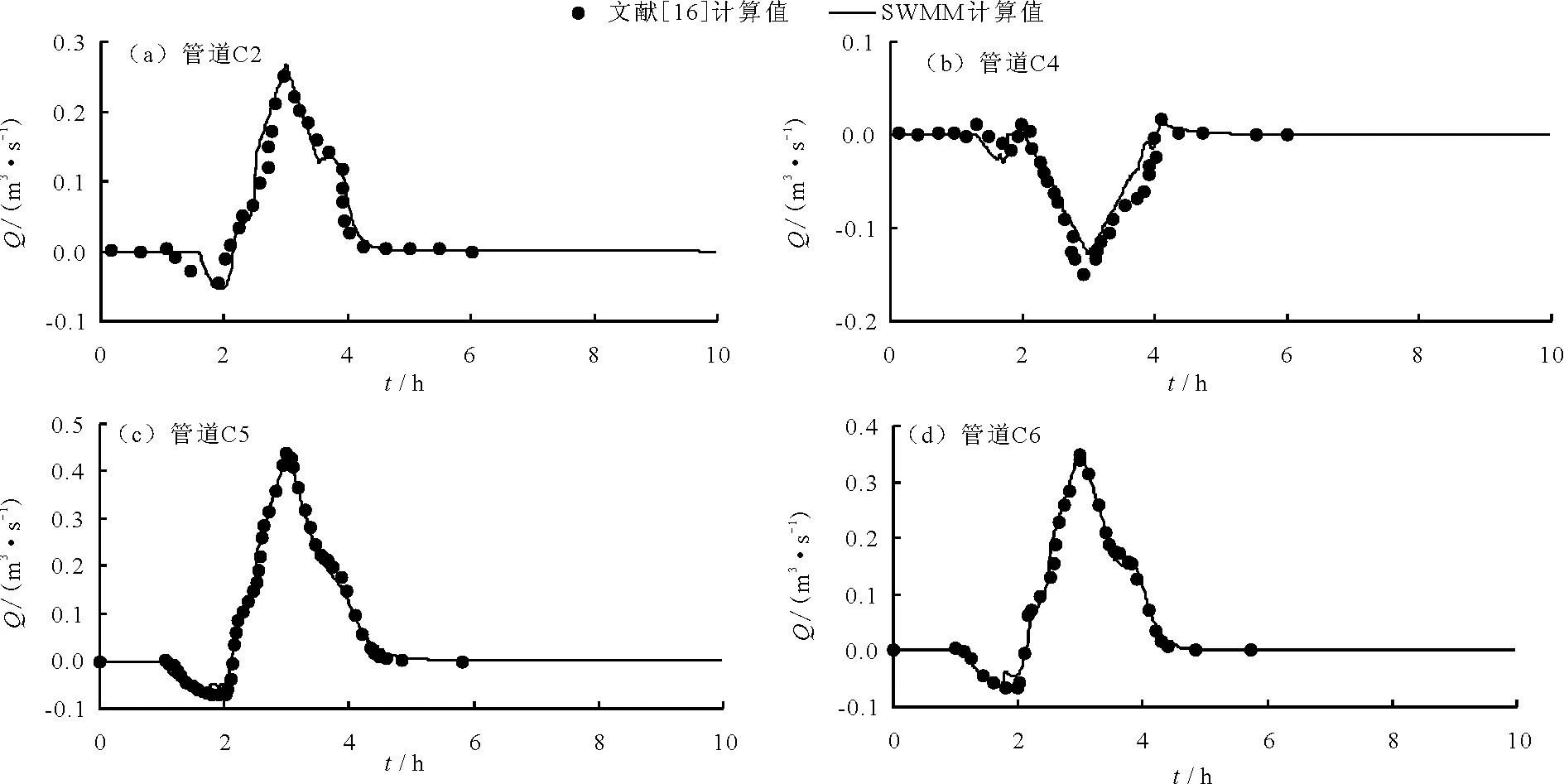
圖8 各管道流量過程

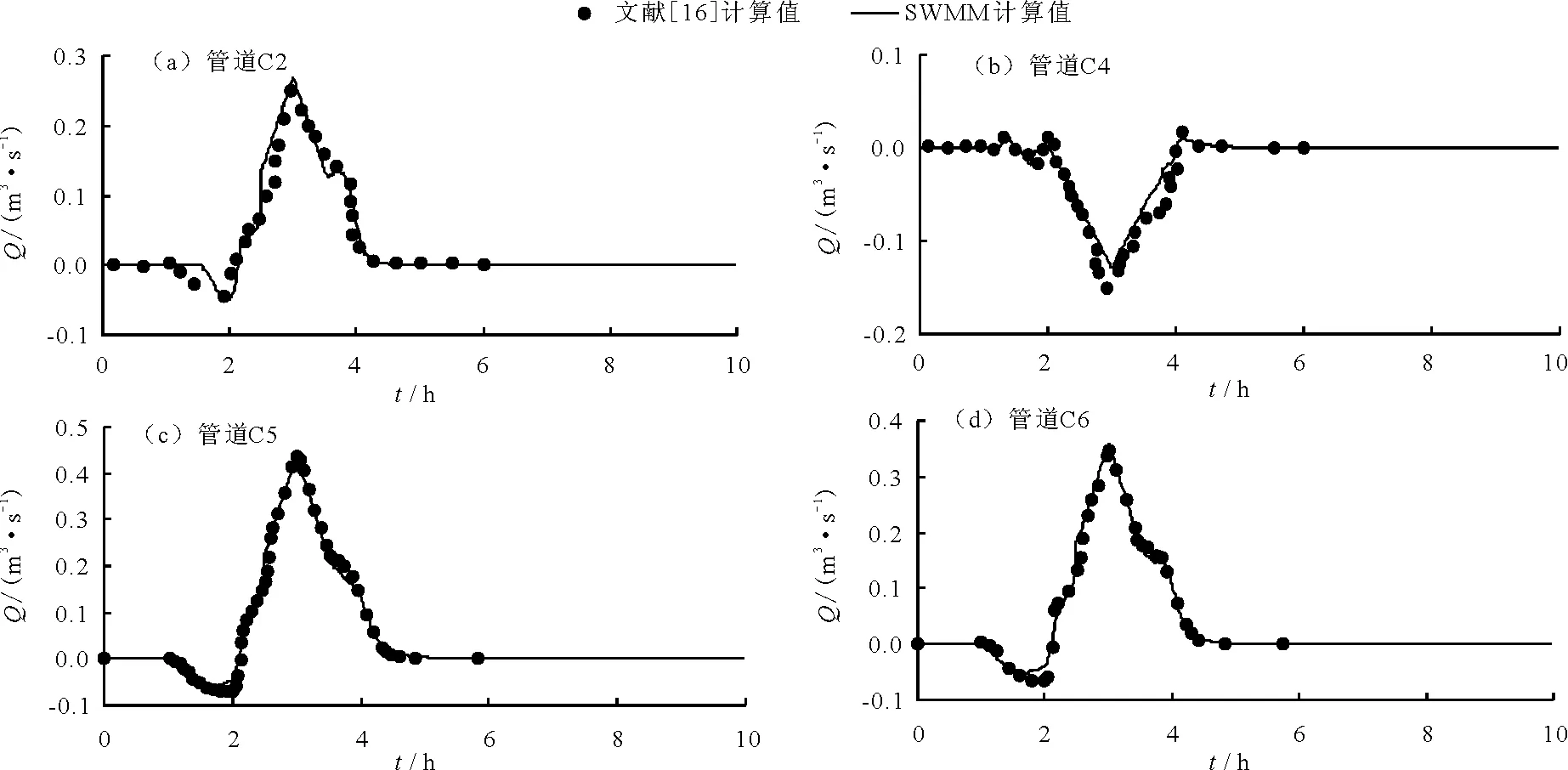
圖9 各管道流量過程

對比和分析圖8與圖9中的計算結果，可以發現，兩種概化方式下SWMM模型的計算結果總體上區別比較小，但采用后一種方式，流量過程更為平滑，與文獻中的結果也更為接近，表明采用SWMM模型時，在管道較長的情況下，適當增加節點的數量，可以在一度程度上改善模型的模擬效果。

5 結 論

(1)采用與常規一維河網模型MIKE11的計算結果進行對比的方式，驗證了SWMM模型中河道概化方式的計算精度，結果表明SWMM模型在保證合適斷面間距的情況下是可以用來城區實際河道的。

(2)采用環狀排水管網算例對SWMM模型處理明滿流的能力進行了驗證，結果表明SWMM具備模擬明滿流的能力，在管道較長時，適當增加中間節點，可以在一度程度上改善SWMM的模擬效果。