動態規劃求解中國象棋狀態總數

魏印福，李舟軍

（北京航空航天大學 計算機學院智能信息處理研究所，北京 100191）

中國象棋是一種廣為流傳的完全知識二人零和博弈游戲，形式上與國際象棋極為相似[1-2]，在博弈技術上二者也有許多共通之處。2016年以來，谷歌相繼推出AlphaGo[3]、AlphaGo Zero[4]、AlphaZero[5]等博弈模型，不僅在圍棋領域完勝人類棋手，在國際象棋、日本將棋上也超越了之前最先進的博弈引擎，計算機博弈受到人們廣泛關注。

中國象棋博弈常提及的一個問題就是中國象棋空間復雜度，即中國象棋狀態總數。現有文獻僅給出中國象棋空間復雜度數值卻沒有提供計算方式，同時不同文獻給出的數值存在較大差異。長期以來，中國象棋狀態總數這一計數問題無人問津，卻又莫衷一是。本文利用中國象棋棋子著法特點把求解中國象棋狀態總數問題分解為若干個子問題，通過動態規劃方法分別求解各個子問題，最終準確求出中國象棋狀態總數，為以后描述中國象棋狀態總數提供可靠依據。同時，這種計算中國象棋狀態總數的方法除了可用于計算其他棋類的空間復雜度，也可以用于構造中國象棋棋盤局面哈希函數[6]、構造中國象棋殘局庫[7-8]等方面。

1 問題描述

1.1 中國象棋棋盤棋子

中國象棋棋盤9條豎線，10條橫線，總計90個位置[9-10]。棋子分為紅黑兩色，每方16枚棋子，棋子分為7類：車、馬、炮、相、士、將、卒。開始局面如圖1所示。

圖 1 中國象棋開始局面Fig. 1 The start state of Chinese Chess

中國象棋中，“將”和“帥”、“相”和“象”、“卒”和“兵”描述的是同一類棋子。為敘述方便，本文對這3類棋子分別采用“將”、“相”、“卒”的叫法。

為便于用公式表示，本文使用英文縮寫表示相關棋子，表1描述了棋子的縮寫及其含義，本文使用縮寫表示棋子，例如使用KR表示紅將，KB表示黑將。

表 1 棋子英文表示及其縮寫Table 1 The chess representation and their abbreviation

1.2 走子規則

車、馬、炮3類棋子可以出現在棋盤的任意位置；相不能過河，只能出現在己方空間中的7個位置，為便于下文敘述，從左到右、從上到下對“相”的可去位置依次編號為0～6，如圖2所示。

圖 2 相的可去位置及其編號Fig. 2 Xiang’s positions and number

士和將只能在九宮格中，士有5個可去位置，將有9個可去位置。如圖3，將九宮格中的9個位置按照從左到右、從上到下的順序依次編號為0～8。

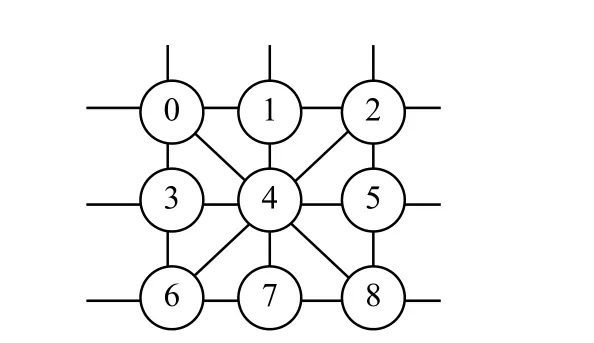
圖 3 九宮格內位置編號Fig. 3 Jiugong position and number

卒的著法分為過河和未過河兩種情況，過河卒可以出現在敵方半棋盤空間中的任意一個位置，未過河的卒只可能出現在己方最上方2行5列共10個位置格點上，并且每列至多有一個卒。

1.3 問題定義

定義中國象棋狀態總數問題首先需要定義子問題：給定若干棋子，在滿足中國象棋規則的情況下，把這些棋子擺放在棋盤上，有多少種可能的放置方式。這里給定的每類棋子個數必然都不大于開局時每類棋子的個數。中國象棋狀態總數可以用式(1)表示，式中S即為中國象棋狀態總數，put表示從棋型到放置方法個數的映射，棋型指14種棋子組成的14維向量，每維數字表示每類棋子的個數。

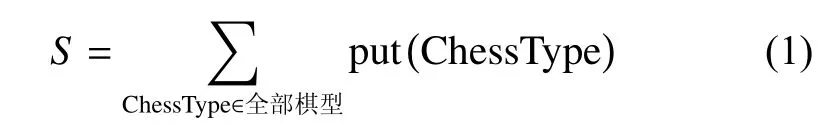
關于計算的中國象棋狀態總數，需要說明3點：

1) 本文討論的是中國象棋可能出現的全部狀態，在每步著法都完美的情況下，從初始狀態出發可能無法到達全部狀態。

2) 本文統計的狀態集合中每個狀態雙方“將”都是存在的，即本文計算的全部局面都是游戲尚未結束的局面。

3) 本文討論的狀態包括“將帥見面”的情況。在中國象棋規則中，促成“將帥見面”局面的一方為輸。

本節對中國象棋棋子、著法進行了簡要介紹，對棋子、棋盤進行了一些符號約定，對問題給出了形式化描述并明確了中國象棋狀態總數所包括的局面。

2 問題求解

2.1 擺放次序

計數問題的兩個基本方法是分類加法和分步乘法[11-12]。當使用分步乘法時，合理的步驟可以減少分類個數[13-14]，從而簡便地解決計數問題。

給定若干棋子之后計算擺放方式的個數時，擺放次序至關重要。下面舉例描述擺放次序的重要性。給定2個紅車、2個紅相共4枚棋子，計算擺放方式個數。車的位置比較隨意，可以擺放在棋盤上90個格點的任意位置，相的位置限制較多，只能擺放在如圖2所示的7個位置上。如果先考慮相再考慮車，可知有 C72×C828種擺放方式；而如果先考慮車再考慮相就需要分3類情況進行討論：

1) 當車占用0個相位時，車有83個位置可選，相有7個位置可選，這種情況有 C823×C72種局面。

2) 當車占用1個相位時，第1個車有7種相位可選，第2個車有83個位置可選，2個相有6個位置可選，這種情況有 C71×C813×C62種局面。3) 當車占用2個相位時，擺放方式有 C72×C52種。

以上3類情況擺法個數之和與“先擺放相，再擺放車”所得結果相同，但顯然第一種方法需要較少的分類討論。由此例可以看出，計算狀態個數時合理規劃擺放棋子的順序能夠極大簡化問題。

計算中國象棋狀態總數時，需按照一定次序放置棋子，核心思想是“先難后易”，即先放置限制較多、活動范圍窄的棋子，然后再放置行動靈活、位置自由的棋子。

2.2 問題分解

車、馬、炮可以到達棋盤上的任何一個位置，放置最為自由，只需要知道棋盤上有多少個空白格點，即可通過排列組合計算出擺法總數，因此最后考慮這3種棋子的擺放。卒過河后可以到達敵方陣地的每一個位置，自由度占半個棋盤，放在倒數第2位考慮。將的位置會影響士相的擺放，相的位置會影響未過河卒子的擺放。考慮將、士、相、卒這4類棋子之間的互相影響關系及著法特點，擬定擺放順序為：將、士、相、卒。

綜上，根據先考慮受限制多的棋子再考慮受限制少的棋子的思路，最終擺放順序為：將、士、相、卒、車馬炮。

利用分步乘法原理依次處理棋子的擺放，這個過程可以對問題進行層層分解，把問題劃分為若干個有依賴關系的子問題。先擺放“將”，“將”擺放完成之后，后面要擺放的“士”和“相”會受到“將”的影響，所以把“將”的位置作為輸入參數向后續求解模塊傳遞。擺放“士”的時候可以根據已擺放“將”的位置，來決定“士”可以擺放的位置有哪些。

整體求解思路為：把已擺放的棋子對未擺放的棋子的影響作為參數傳遞給后續子問題，擺放棋子時參考已擺放棋子的位置來決定當前可行的擺放方法。

本節詳細描述把中國象棋擺法總數這個問題劃分成將、士、相、卒、“車馬炮”5個子問題，每個子問題都有明確的輸入，每個子問題的輸出都是擺法個數。子問題之間逐層調用，最終能夠求得中國象棋狀態總數。子問題的定義及其輸入的形式化是整個求解過程中較為關鍵的部分。

2.2.1 將

先擺放好雙方的“將”，再考慮子問題：在“將”位置確定的情況下，“士相卒車馬炮”總共有多少種擺法。記此子問題為getShi(KR, KB)，該子問題輸入KR, KB為紅黑雙方“將”的位置。

對“將”的每一種擺放方式，將其余棋子的擺法個數累加起來即為中國象棋狀態總數。偽代碼如下：

函數名稱 getJiang

輸入 無；

輸出 擺法種數s。

1) s = 0；

2) 對于紅將的每個位置KR∈[0, 9)；

3) 對于黑將的每個位置KB∈[0, 9)；

4) s+=getShi(KR, KB)

在以上代碼中，KR表示紅方將的位置，KB表示黑方將的位置，累加雙將位置確定之后“士相卒車馬炮”的擺法個數即得到中國象棋狀態總數，如式(2)：

2.2.2 士

在2.2.1中，在給定“將”位置的情況下，需要計算“士相卒車馬炮”有多少種擺法。當“將”的位置確定后，“士”的可選位置隨之確定。如果“將”在圖3中的0、2、4、6、8號位置，則“將”占用一個士位，“士”有4個位置可選；如果“將”在1、3、5、7、9號位置，“將”沒有占領士位，士有5個位置可選。

對于“士”的每一種擺法，累加“相卒車馬炮”的擺法個數，即可得到在“將”位置確定情況下“士相卒車馬炮”的擺法個數。記子問題“相卒車馬炮”的擺法個數為getXiang(KR, KB, SpaceR, SpaceB)，其中KR、KB輸入表示紅黑雙方將的位置，SpaceR、SpaceB表示雙方空白格點數。getShi函數輸入參數為紅將位置和黑將位置，輸出“士相卒車馬炮”擺法總數。偽代碼如下：

函數名稱 getShi

輸入 紅將位置KR；黑將位置KB；

輸出 “士相卒車馬炮”的擺法總數s。

1) s=0；

2) 定義紅士可去位置個數：若KR不在士位上NR=5，否則NR=4；

3) 定義黑士可去位置個數：若KB不在士位上NB=5，否則NB=4；

4) 對于紅士個數的可取值AR∈{0, 1, 2}；

5) 對于黑士個數的可取值AB∈{0, 1, 2}；

6) 紅方空白格點數SpaceR=45-1-AR；

7) 黑方空白格點數SpaceB=45-1-AB；

8) s+=CNARRCNABBgetXiang(KR, KB, SpaceR, SpaceB)

在上述偽代碼中，擺放好“士”之后，需要乘以“相卒車馬炮”的擺法個數，“相卒車馬炮”擺法個數通過getXiang函數實現。考慮已擺放的“將”、“士”對“相卒車馬炮”的影響，可以發現后續棋子的擺放只依賴于紅將位置、黑將位置、紅方空白格點數、黑方空白格點數4個變量。

2.2.3 相

經過以上兩步，“將”和“士”的位置確定了，這兩種棋子對后續棋子的“影響因素”包括：

1) “將”可能會占用相位，影響“相”的可擺放位置的個數；

2) 紅方和黑方各自的空白格點數，影響“卒車馬炮”的擺放。

問題轉化為給定“將”的位置和紅黑雙方空白格點個數之后，“相卒車馬炮”有多少種擺法。

“相卒車馬炮”的擺法只跟4個變量有關：紅將位置、黑將位置、紅方空白格點數、黑方空白格點數。這4個變量一旦確定，“相卒車馬炮”的擺法個數便隨之確定。求解子問題“相卒車馬炮”需要先考慮相的擺法。根據“將”是否已經放在如圖3的1號位置，可以確定相的可選位置的個數。

對于“相”的每一種擺法，累加“卒車馬炮”的擺法個數，即得“相卒車馬炮”的擺法總數。記子問題“卒車馬炮”的擺法個數為getZu(BPR, BPB,SpaceR, SpaceB)，BPR、BPB分別表示紅相、黑相占用卒位的個數，SpaceR、SpaceB分別表示紅黑雙方空白格點數。偽代碼如下：

函數名稱 getXiang

輸入 紅將位置KR；黑將位置KB；紅方空白格點數SpaceR；黑方空白格點數SpaceB；

輸出 “相卒車馬炮”的擺法總數s。

1) 定義紅相可去位置個數：若KR不在相位上NR=7否則NR=6；

2) 定義黑相可去位置個數：若KB不在相位上NB=7否則NB=6；

3) s=0；

4) 對于紅相個數的可取值BR∈{0, 1, 2}；

5) 對于黑相個數的可取值BB∈{0, 1, 2}；

6) 對于紅相占用紅卒位置的個數BPR∈{0, 1, 2}；

7) 對于黑相占用黑卒位置的個數BPB∈{0, 1, 2}；

8) 相的放法種數 placeXiang=CBPRCBPBCBR-BPR

22NR-2 CBB-BPB；NB-2

9) s+=placeXiang×getZu(BPR, BPB, SpaceR-BR,SpaceB-BB)。

2.2.4 卒

經過以上步驟，“將士相”擺放完成，“卒車馬炮”子問題的輸入包括4個變量：紅相占用卒位個數(可取值0、1、2)、黑相占用卒位個數(可取值0、1、2)、紅方空白格點數、黑方空白格點數。

“卒”需要分為2類進行討論：過河卒和未過河卒。各方過河卒個數加上未過河卒的個數不超過5，需考慮紅方、黑方各自的過河卒、未過河卒共4類棋子的擺放。

為便于敘述，下面進行一些符號約定：

1) SpaceB表示黑方棋盤空白格點數，SpaceR表示紅方棋盤空白格點數；

2) PR表示紅方未過河卒的個數，PB表示黑方未過河卒的個數；

3) P′R表示紅方過河卒的個數， P′B表示黑方過河卒的個數。

下面以紅方為例，討論過河卒和未過河卒的擺放。

對于過河卒，有 CP′

R

種擺法，其中

SpaceB-PB

SpaceB-PB表示黑方空白格點數，從這些空白格點選擇 P′

R個格點分配給 P′R個紅方過河卒。

對于紅方未過河卒，需要根據相占用的卒位個數和未過河卒的個數兩個變量求出有多少種放置方法，這個問題可以明確定義為：在2行5列共10個位置上，放置P個卒子，其中BP個相占用了卒位，每列至多放置1個卒子，在這些約束下求P個卒子的擺法總數。這個子問題解法如下：假設有i個卒子放在了被占用的列上，這i個卒子只有唯一位置。而剩下的P-i個卒子都有2個空白格點可選，共計2P-i種情況。未過河卒放法種數如式(3)所示：

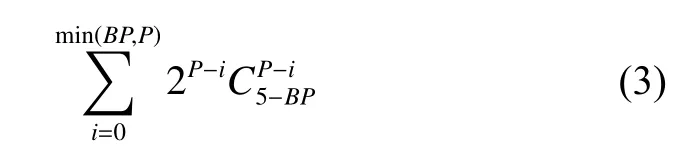
對于卒子的每一種擺放方式，累加“車馬炮”的擺放方式即得“將士相”確定后，“卒車馬炮”的擺放方式。

2.2.5 車馬炮

“車馬炮”的擺放僅與一個變量有關，即整個棋盤上空白格點數。枚舉紅黑雙方車、馬、炮的個數，使用分步乘法計算有多少種擺法，如式(4)：

jvmapao(RB, RR, HB, HR, CB, CR)函數可以使用分步乘法實現。例如，擺完“將相士卒”之后剩余80個空白格點，在這些空白位置上擺放2個紅車、2個紅馬、2個黑炮。根據分步乘法很容易得出擺法總數為 C820×C728×C726。jvmapao函數實現如以下偽代碼所示：

函數名稱 jvmapao

輸入 空白格點數Space；紅黑雙方的車馬炮的個數RB、RR、HB、HR、CR、CB；

輸出 s，表示“車馬炮”的擺法總數。

1) s=CRB×CRR；SpaceSpace-RB

2) Space=Space-RB-RR；

3) s=s×CSHpBace×CSHpRa ce-HB；

4) Space=Space-HB-HR；

5) s=s×CCB×CCR。SpaceSpace-CB

2.3 動態規劃方法加速求解

利用2.2節中各個子問題的性質，可以對上述計數方法進行優化。各個部分輸入參數如圖4。

圖4描述了中國象棋狀態總數求解的5個子問題：

1) 將的擺放；

2) 士的擺放，輸入為紅將、黑將的位置；

3) 相的擺放，輸入為紅將、黑將的位置、紅黑雙方空白格點數4個變量；

4) 卒的擺放，輸入為紅黑雙方空白格點數、紅黑雙方相占用卒位的個數；

5) 車馬炮的擺放，輸入為整個棋盤上空白格點 數。

每個子問題都有一條重要性質：輸入到輸出為單射。根據這條性質可以為每個子問題建立一個映射表，保存函數輸入和輸出的映射關系。當求解某個子問題時，先查詢映射表，如果存在答案則不必再調用后續子問題進行求解，直接查表得出；如果不存在，則求解該問題并把最終結果存儲到映射表中，以備下次查詢。這種方法相當于為每個子問題加一層緩存，若未命中緩存則進行求解并使用求解結果更新緩存，若命中緩存則直接返回緩存的答案。這種動態規劃技巧又叫備忘錄方法[15-18]，是動態規劃的一種變形。

各個子問題之間具有單向依賴性，動態規劃方法避免了子問題之間?層層調用和重復調用。

3 實驗結果與驗證

實驗得出中國象棋狀態總數具體數值為7 547 040 878 332 418 571 694 532 043 654 081 760 159，用科學計數法表示為7.54×1039.88。現有文獻中提到的中國象棋狀態總數如表2所示，這些結果都遠遠高估了中國象棋空間復雜度。

表 2 參考文獻中中國象棋空間復雜度Table 2 The Space Complexity of the Reference Document

如果用定長編碼來描述中國象棋的一個狀態，只需對中國象棋狀態總數取以2為底的對數，得到結果132.47 bit，這就是描述一個棋盤狀態最少需要的bit數。若將中國象棋全部狀態使用定長編碼存儲下來，需要將狀態占用bit數乘以狀態個數，結果為1.14×1029TB。

為佐證本文結論，使用另一種粗略方法估計中國象棋狀態總數。下面給出一種簡略的計算中國象棋狀態總數的方法，這種方法給出的是中國象棋狀態總數的上界。

首先，只考慮紅方的棋子擺放，記為s。中國象棋包括紅方和白方兩方，所以全部狀態總數為s2。下面介紹s的計算方法。

將和士擺放方法為 j iangShi=C93×3+C92×2+C91。將士在九宮中， C93表示選定3個位置，乘以3表示為“將”分配3個位置中的1個位置。

相的擺放方法數為： xiang=C72+C71+C70。卒的擺放需要考慮過河卒和未過河卒，過河卒有4放5方個式格。點故空卒間的，擺未放過方河式卒有有zu5=∑列5i=，0∑每5j=-列0iC有4i5×2C種5j×擺2j種。車的擺放方式： jv=C920+C190+C900。馬和炮的擺法與車完全相同。

在這種簡略計算方法中，忽略了棋子之間的互相影響，所以應該采用分步乘法的方式計算s，只考慮紅方共有s=jiangShi×xiang×zu×jv3種擺法。

中國象棋狀態總數即為s2，約為1042.78。可見粗略估計結果與本文計算結果更為接近，即便是粗略估計，現有文獻中的數據都是極不準確的。

4 結論和展望

基于動態規劃的方法求解中國象棋狀態總數充分挖掘了中國象棋棋子著法規律，快速而準確地求出了中國象棋狀態總數，為描述中國象棋空間復雜度提供了充分依據，實驗證明現有文獻提供的數據遠遠不夠準確。

該計數方法創新點包括兩方面：1)先難后易，把問題分解為若干個子問題，先擺放約束較多的棋子，后擺放約束較少的棋子，把影響后續擺放的因素作為參數向后傳遞；2)在求解每個子問題時，動態規劃可以減少重復計算。

本文提出的計數方法可能的應用方向包括：1)計算其他博弈游戲狀態總數；2)用于構造中國象棋棋盤局面哈希函數，建立棋盤局面和數字之間的一一映射；3)尋找可暴力枚舉全部狀態的棋型，為構建中國象棋殘局庫提供依據。