圓端空心墩地震損傷評估及抗震性能目標研究

吳維洲 邵長江 胡晨旭 章健華

(1.成蘭鐵路有限責任公司， 成都 610032； 2.西南交通大學， 成都 610031)

橋墩地震損傷機理和狀態評估方法是混凝土橋墩抗震研究的重要內容，能夠快速準確的定量震損結構的損傷等級，進而確定搶修策略及維修加固方法，是震后搶險救災、搶通保通的關鍵性基礎問題，也是災后重建、恢復經濟、發展生產的重要技術和理論手段。因而，運用合理方法定量描述結構的地震損傷，對結構的抗震設計以及損傷評估至關重要。

空心墩是山區高墩大跨橋梁的優選墩型，如何評估在強震區鐵路高墩橋梁在未來地震下的損傷情況，給出抗震設計的性能目標，對于提升此類橋梁的抗震性能具有重要意義。國內外學者已經發展了多種地震損傷模型，主要包括強度準則、延性損傷、剛度退化損傷、變形損傷、低周疲勞損傷、能量損傷等單參數損傷模型。隨著實際震害經驗的增加，人們逐漸認識到單一首超破壞或累積損傷難以真實反應構件的破壞機理。基于上述認識，各國學者相繼提出了大量雙參數地震損傷模型。

Park和Ang[1]最早根據試驗資料提出了以最大位移和累積滯回耗能為參數的損傷模型，引領了雙參數損傷模型的研究熱潮，但因采用位移與能量的線性組合，存在位移項對破壞狀態損傷指標的影響隨位移的增大而減小、能量項對破壞狀態損傷指標的影響隨位移的增大而增大、上下界不收斂、極限損指標大于1.0等問題，其他研究人員從不同角度提出了改進模型，如Kunnath[2]等引入構件屈服變形的改進模型；王東升[3]等人基于加載路徑有關的能量項加權因子模型；Kumar[4]等人考慮加載歷程的模型；牛荻濤[5]等人的變形與耗能的非線性組合模型；李軍旗[6]等人損傷變量變化率與強度衰減率成正比模型；傅劍平[7]等人針對位移引進指數函數調節項的模型；付國[8]等人的耗能分解為有效耗能與無效耗能的模型；羅文文[9]等人基于Miner準則的模型；陳林之[10]等人考慮上下界不收斂問題和模型；曾武華[11]等人基于標準化塑性變形與標準化累積滯回耗能組合模型，這些模型雖然形式多樣，但從根本上均認為損傷指數是正則化最大變形和滯回能耗的線性疊加，能夠同時考慮變形與滯回耗能對構件損傷的影響，使得計算公式簡單易行，能夠在構件層次上反映結構的損傷特性。因此，被廣泛用于各類結構或構件的地震損傷評估。

鑒于空心墩與實心墩力學性能的差異，以及不同的損傷模型適用范圍不同，上述基于鋼筋混凝土實心墩柱試驗結果建立的損傷模型對空心墩的適用性尚不明確。為準確評估地震荷載作用下空心墩的損傷狀態，需對既有損傷模型進行深入的研究，從而得出鐵路圓端空心墩地震損傷評估的推薦公式和評估方法。

1 損傷評估模型

根據上述文獻，在已有的鋼筋混凝土結構、構件損傷模型中，基于變形與能量的Park-Ang損傷模型應用范圍最廣，以下分別介紹該模型及其改進形式。

Park和Ang較早注意到剛度退化的影響，根據大量梁柱構件的破壞試驗，提出了最大變形-累積耗能的線性組合損傷模型[1]，開啟了地震損傷評估方法的研究熱潮。

(1)

式中：δm——構件在地震下的最大變形；

δu——構件在單調荷載下的極限變形能力；

Fy——構件的屈服強度；

dE——塑性應變能的增量。

參數β如下：

β=(-0.357+0.73λ+0.24n0+0.31ρt)0.7ρw

(2)

式中：λ——剪跨比；

n0——軸壓比；

ρt——配筋率；

ρw——配箍率。

Kunnath等人在Park-Ang模型基礎上，考慮構件屈服變形δy的影響，提出了改進模型的形式[2]：

(3)

式中：δy——構件屈服位移。其余同式(1)。

王東升等人通過引入與加載路徑有關的能量項加權因子改進了Kunnath地震損傷模型[3]：

(4)

式中：Ei——第i個滯回環所包圍的面積(即滯回耗能)；

βi——與加載路徑有關的能量項加權因子。

與此類似，Kumar等人考慮了加載歷程對構件損傷的影響，給出的Park-Ang改進模型[4]：

(5)

式中：δm,j——最大變形；

Nj——首次產生δm,j的半周期數；

N——半周期總數；

Ei——第i個半周的累積塑性耗能；

β，c——參數，β=0.11，c=1，其余參數同上。

牛荻濤等人提出了變形與耗能的非線性組合形式[5]：

(6)

式中：α、β1——組合系數，α=0.138 7，β1=0.081 4；

E、Eu——結構的滯回耗能，結構的極限滯回耗能。

李軍旗等認為循環荷載的損傷表現在最大變形時構件產生的強度退化，而加載歷程對累積損傷的貢獻反映在強度衰減上[6]：

(7)

式中：ηp——強度衰減系數；m=1.3+3.5n0(n0為軸壓比)。

傅劍平等人的改進模型中位移項對損傷指標的影響隨位移的增大而增大，能量項對損傷指標的影響隨位移的增大而減小，從而修正了Park-Ang模型的缺陷[7]，模型如下：

(8)

式中：μm——構件的最大延性系數，其余符號同上。

付國等人修正了Park-Ang模型的能量項，把滯回耗能劃分為有效耗能及無效耗能，考慮了有效耗能部分以及不同加載幅值下滯回耗能對構件破壞的影響[8]：

(9)

(10)

式中：ei——第i次加載的有效耗能因子；

Ei——第i次加載的累積塑性耗能；

δim——第i次加載的位移幅值，其余符號同前。

針對Park-Ang模型無法考慮最大滯回耗能與加載路徑的關系、單調加載時損傷指數大于1等問題，羅文文等基于疲勞理論和Miner準則，提出了修正模型[9]：

(11)

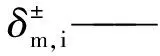
β、γ——均為參數，其余符號同上。

陳林之等人根據PEER數據庫和自有試驗結果對能量項加權系數進行回歸分析得到改進模型[10]：

(12)

式中：參數及符號同上。

曾武華等人提出基于歸一化塑性變形及歸一化、化累積耗能的損傷模型，解決了Park-Ang模型上下界不收斂的問題，在輕微破壞和中等破壞極限狀態下損傷指標限值相對于損傷指標離散性顯著降低。塑性變形引起的損傷DD和滯回能量引起的累計損傷DE的組合形式的損傷指標[11]。

D=1-(1-DD)/(1+DE)

(13)

DD=δm-δy/(δu-δy)

(14)

DE=Eh/(Fyδu)

(15)

式中：Eh——地震反應循環中力-位移曲線所包圍面積總和。

2 圓端空心墩擬靜力試驗

為研究鐵路圓端空心墩的地震損傷機理及評估方法，設計并進行了5個空心墩的擬靜力試驗，加載系統如圖1所示，設計參數如表1所示。

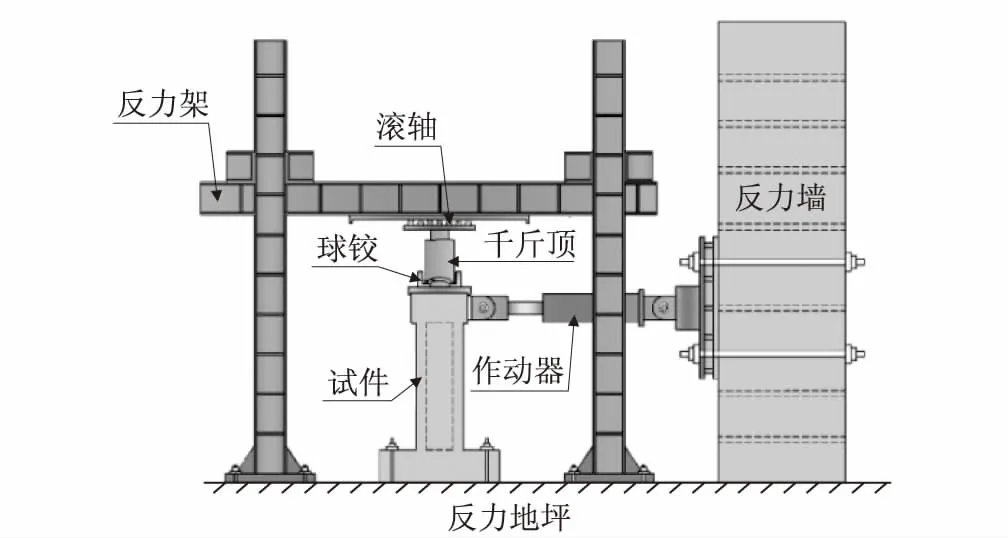
圖1 擬靜力加載系統

表1 模型設計參數

3 損傷評估

3.1 損傷過程描述

試驗加載的滯回曲線，如圖2、圖3所示，限于篇幅，在此僅給出部分橋墩的實測結果。由試驗現象可知，5個空心墩的損傷情況大致相同，經歷了混凝土出現微裂縫、局部出現貫通裂縫及縱筋屈服、混凝土保護層脫落、混凝土保護層大面積剝落及縱筋裸露、縱筋壓屈(S-A3為縱筋斷裂)這一過程。5個試驗墩均為彎曲破壞，塑性鉸區域混凝土裂縫較寬，裂縫數量多且較為集中，極限狀態下，角隅處縱筋裸露明顯，受壓區混凝土壓潰現象顯著，損傷情況較為嚴重。

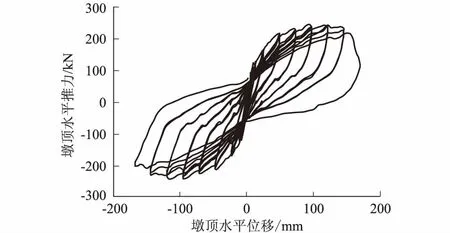
圖2 試件S-A1滯回曲線

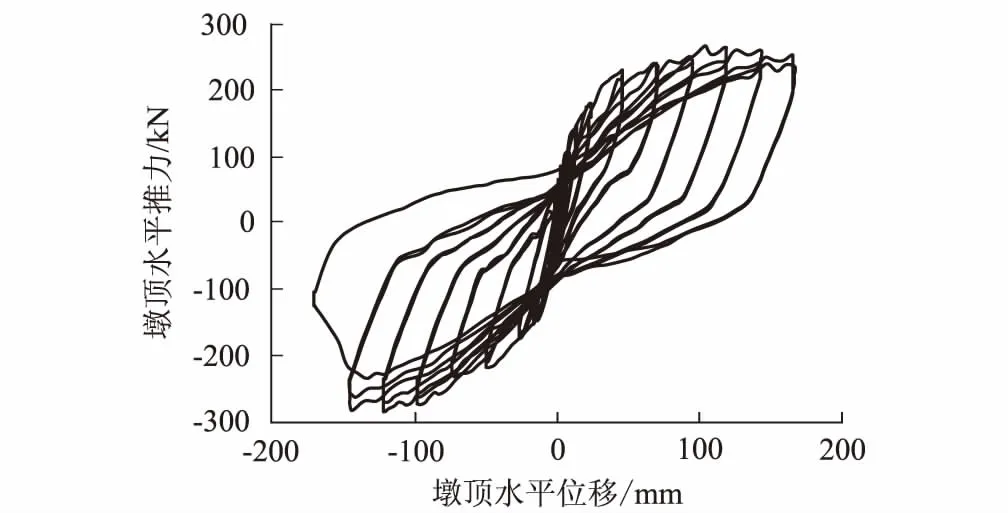
圖3 試件S-A2滯回曲線

3.2 損傷水平劃分及損傷狀態評估

鋼筋混凝土的破壞狀態及抗震性能目標可劃分為5個等級[12]：(1)基本完好：僅有局部不貫通的微裂紋；(2)輕微損傷：產生內外貫通的細小微裂紋；(3)中等損傷：裂紋清晰可見，局部混凝土保護層剝落或產生碎片；(4)嚴重損傷：宏觀裂紋顯著變寬，局部混凝土保護層完全剝落；(5)倒塌狀態：核心混凝土壓碎或縱筋拉斷、壓屈、橫向鋼筋拉斷等。

為分析方便，現將上述損傷模型依次編號為M1-M11。基于上述模型的地震損傷演化曲線，如圖4所示(僅列出S-A1)。由空心墩的損傷指數發展曲線可知，空心墩損傷指數發展趨勢：前期增長較為緩慢，隨著循環次數的增加，損傷指數的增加較快。不同模型的損傷曲線的離散性很大。

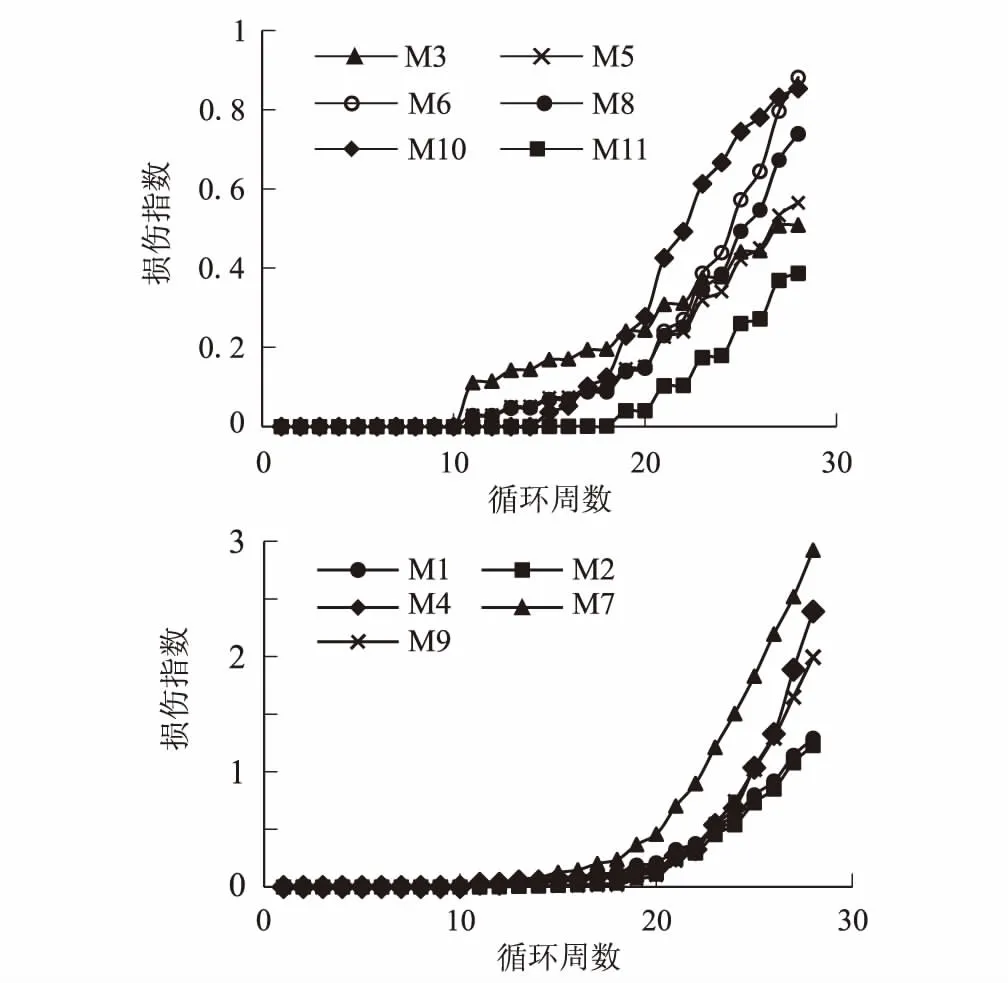
圖4 S-A1損傷演化曲線

對比試驗現象及各損傷狀態下不同損傷模型的損傷指標，如表2所示。由表2可以發現：

(1)Park-Ang、傅劍平等人能夠合理評估構件的無損傷狀態及輕微損傷程度，而傅劍平等人的公式卻高估了構件后期的損傷水平，在嚴重損傷時，損傷指標大于1，與試驗現象不吻合。

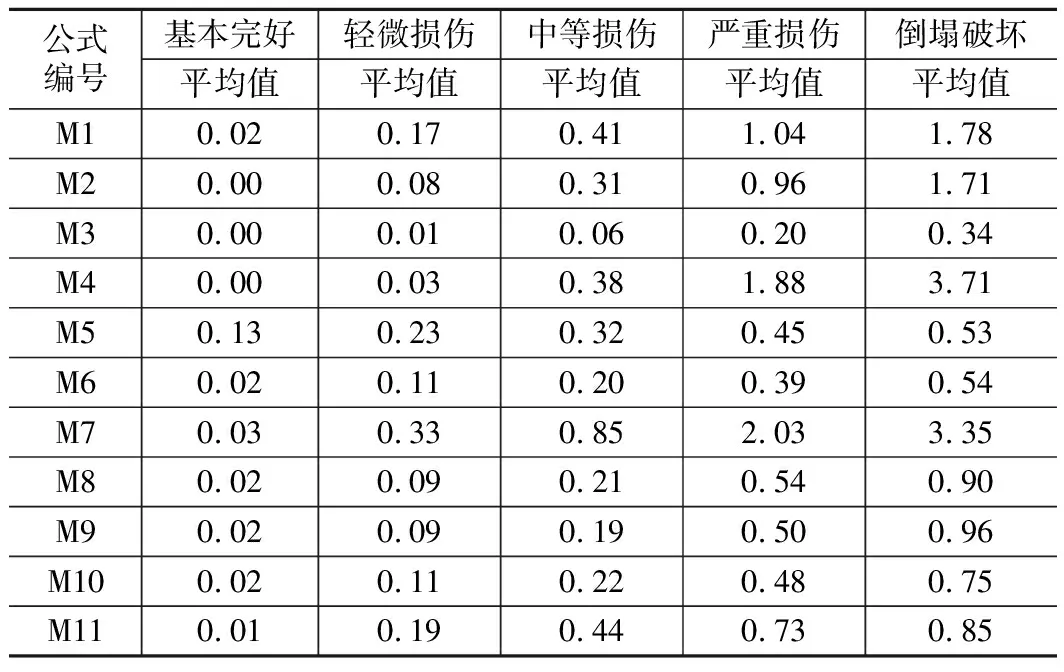
表2 空心墩不同損傷程度的損傷指標均值及標準差

(2)Kunnath、Kumar等人在前期低估了構件的輕微損傷，對構件中等損傷的評估較為合理，但高估了后期嚴重損傷狀態；王東升等人的公式、Bracci公式低估了構件各個狀態(除基本無損壞狀態)的損傷，與試驗結果差異較大。

(3)牛荻濤等人高估了基本無損壞狀態的損傷，對輕微損傷和中等損傷的評估較為合理，與試驗現象吻合，低估了后期嚴重損傷狀態的破壞程度。

(4)李軍旗、付國、羅文文等人均低估了構件輕微損傷的破壞，對中等狀態的損傷評估趨于合理，李軍旗公式低估了構件嚴重損傷狀態及倒塌狀態的破壞程度，而付國、羅文文對后期損傷狀態的評估較為合理，能夠反映構件實際的損傷過程，與試驗結果一致。

(5)曾武華等人模型能夠合理反映整個試驗過程中構件的破壞情況，與構件的實際損傷程度較一致，可作為空心墩損傷評估的推薦方法。

選擇位移比作為彎曲破壞試驗構件的量化指標，同時引入損傷指數(D)表征試件的損傷程度，建立位移比與損傷指數的聯系。采用曾武華等人損傷模型[11]計算各橋墩不同工況下的損傷指數，該指數在[0,1]之間單調增長，D=0表示構件完好無損，D=1表示構件完全破壞，當D為其它值時，構件處于相應的損傷狀態。橋墩各特征狀態下的位移比與損傷指數計算結果，如表3所示。

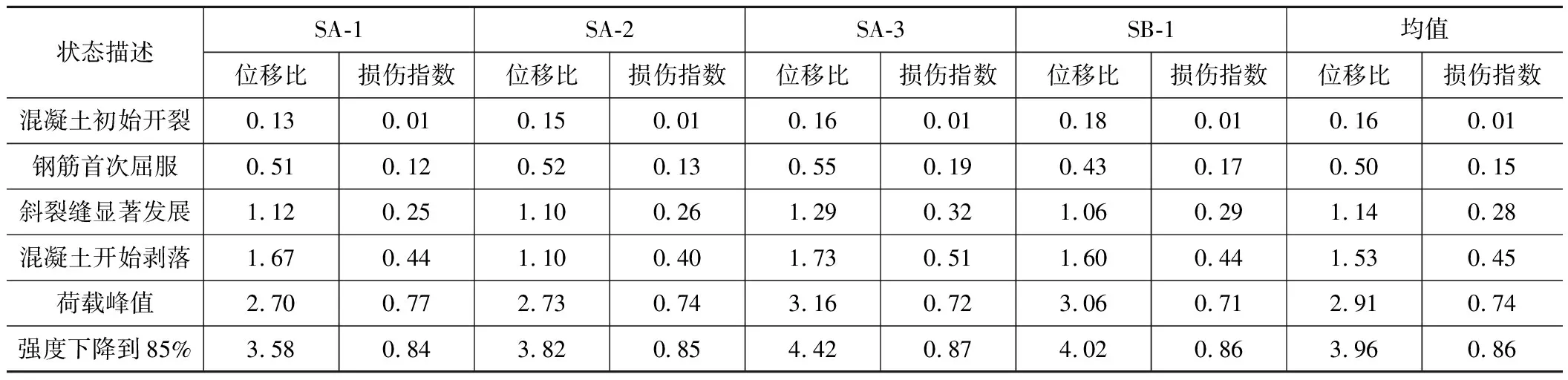
表3 試驗構件性能量化結果

3.3 性能目標量化

為了更直觀描述各變形狀態下試件的損傷程度，通過損傷指數對橋墩損傷狀態進行量化，并于不同水準對應起來(見表4)，通過該表可知：試件位移比在0.5以內時，損傷指數在0.15以內，損傷程度很小，試件處于功能良好狀態；當試件位移比在0.5～1.3之間時，損傷指數在0.2～0.4之間，試件開始進入非線性，發生微小損傷；當位移延性比達到3時，損傷指數達到0.75，損傷程度很大，試件經歷強非線性、進入嚴重損傷階段；當位移比超過4時，損傷指數超過0.85，損傷程度非常大，試件承載力下降到最大側向力的85%。

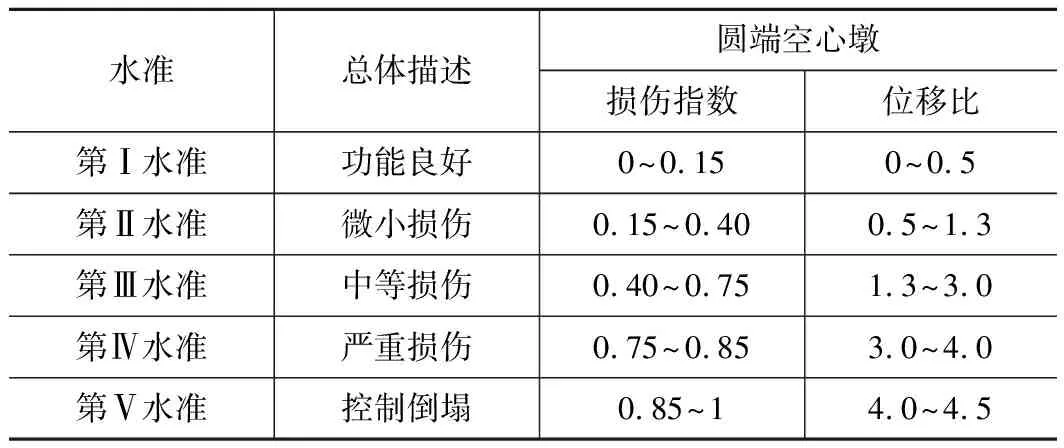
表4 基于損傷指數的性能目標量化

4 結論

文章利用5個鐵路圓端型空心墩的擬靜力試驗結果，分別計算出11個損傷模型關于構件的損傷指標，并與試驗現象對比分析，可得出以下結論：

(1)橋墩均發生了典型的彎曲破壞，表現較好的延性性能。

(2)對比試驗現象和量化結果，曾武華損傷模型適于鐵路混凝土圓端空心墩的地震損傷評估。

(3)位移比、損傷指標和損傷現象的對比表明，作者建立的三者之間定量關系，可以合理確定鐵路圓端空心墩的抗震性能目標。