固定鴨舵導引組件修正力模型改進及參數辨識

馮斌， 于紀言， 王鈺， 王曉鳴， 鞠潭

(南京理工大學 智能彈藥技術國防重點學科實驗室， 江蘇 南京 210094)

0 引言

彈道修正彈的彈道預測和修正指令的生成均需要準確的氣動力數據，而將彈丸受到的氣動力與彈丸狀態參數聯系起來建立氣動力模型，可以為彈丸氣動外形設計、彈道設計以及彈丸飛行性能分析提供幫助。固定鴨舵雙旋修正彈將帶有固定鴨舵的修正組件(見圖1)和彈體在旋轉通道解耦，彈體的高速旋轉保證飛行穩定，修正組件低速轉動，調節由舵面產生的修正力方向，從而實現彈道修正。建立準確的導引組件修正力氣動工程模型對于修正彈飛行特性研究具有重要意義。

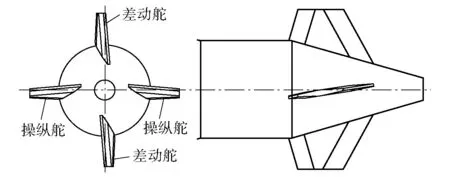
圖1 4°舵偏固定鴨舵雙旋修正彈修正組件模型Fig.1 Dual-spin projectile correction kit with 4° canard deflection

目前，國內外對雙旋彈道修正彈的氣動特性研究主要從數值計算和風洞試驗兩個方面進行。Jermey[1]采用風洞試驗對帶鴨舵的彈丸進行測力試驗。吳萍等[2]通過風洞試驗方法對帶鴨舵的彈丸氣動特性隨馬赫數、攻角以及舵偏角的變化規律進行了研究。SAHU等[3-4]采用非結構嵌套網格的方法實現了多自由度模擬飛行，為本文計算方法的選取提供了參考。紀秀玲等[5]通過數值計算研究了隔轉鴨舵雙旋彈縱向氣動特性，通過數值仿真得出鴨舵相位角和全彈法向力、俯仰力矩變化呈三角函數關系的結論。許安勇[6]也進行了相應數值研究，通過計算彈丸各修正狀態的陀螺穩定因子和動態穩定因子，得出彈丸各修正狀態均具有良好飛行穩定性的結論。Liang等[7]將優化算法與數值計算結合起來，對固定鴨舵雙旋修正彈的鴨舵外形進行優化。殷婷婷等[8]對固定鴨舵導引組件的控制模型進行了創新，提出了一種結合數值仿真和試驗測試的建模方法，通過將修正組件置于自由射流風洞中對模型進行驗證。程杰等[9]基于小擾動理論建立的關于雙旋修正彈工程模型應用較為廣泛。該模型將修正組件的4片固定鴨舵舵片分為提供修正側向力的操縱舵舵片和提供組件反轉力矩的差動舵舵片兩組。基于小擾動理論將每組舵片的氣動力分解為受橫向繞流產生的攻角效應和受軸向繞流產生的舵偏效應。模型相關參數利用風洞試驗得到的數據進行參數辨識和驗證，但是以兩組舵片受力疊加方式仍存在無法精確表示導引組件的修正力問題。根據其模型可知導引組件的修正力在只存在于垂直操縱舵舵片的方向，但是客觀物理現象是存在攻角時，迎風側與背風側舵片受力差異導致差動舵舵片也能產生修正力。

因此，本文基于小擾動理論分別考慮4片舵片氣動力建立導引組件的修正力氣動工程模型，并對工程模型中的相關參數使用Levenberg-Marquardt(L-M)算法[10]進行辨識。準確的導引組件修正力模型建立為后續通用性研究和修正彈飛行特性的研究奠定了基礎。

1 數值方法驗證

本文基于氣動力數據進行雙旋修正彈導引組件氣動工程模型的建立和參數辨識，由于風洞試驗六分量天平能測得全彈氣動力，但無法直接獲得導引組件部分氣動力，因此還需要依靠計算流體力學(CFD)方法獲得更詳細的導引組件部分氣動力。在此之前，通過對比風洞試驗六分量天平測得全彈氣動力數據和數值計算得到的全彈氣動力結果，驗證數值計算的有效性。

1.1 風洞試驗

風洞試驗在南京理工大學HG04超聲速風洞中進行。HG04風洞為直流下吹暫沖式閉口跨超聲速風洞, 采用固塊式二元噴管，可以通過更換不同噴管來改變馬赫數,試驗段橫截面面積為0.3 m×0.3 m，試驗段長0.6 m. 在試驗段兩側開有光學玻璃觀察窗，尺寸為0.29 m×0.16 m，便于在試驗過程中觀測模型姿態或進行紋影照相。試驗模型及其在風洞中的安裝如圖2和圖3所示。

圖2 風洞試驗所用模型Fig.2 Model for wind tunnel experiment

圖3 試驗模型在風洞中的安裝圖Fig.3 Physical model mounted in wind tunnel

1.2 數值計算以及結果對比

為了驗證數值計算方法的有效性，需對雙旋彈所在計算域進行三維建模和空間離散。圖4所示為4°舵偏的雙旋彈計算域網格，計算域按照空間分布，分解為鴨舵繞流區、彈體繞流區和外部流場。對計算域進行空間離散生成非結構六面體單元計算網格。圖5所示為4°舵偏的雙旋彈彈體表面網格。

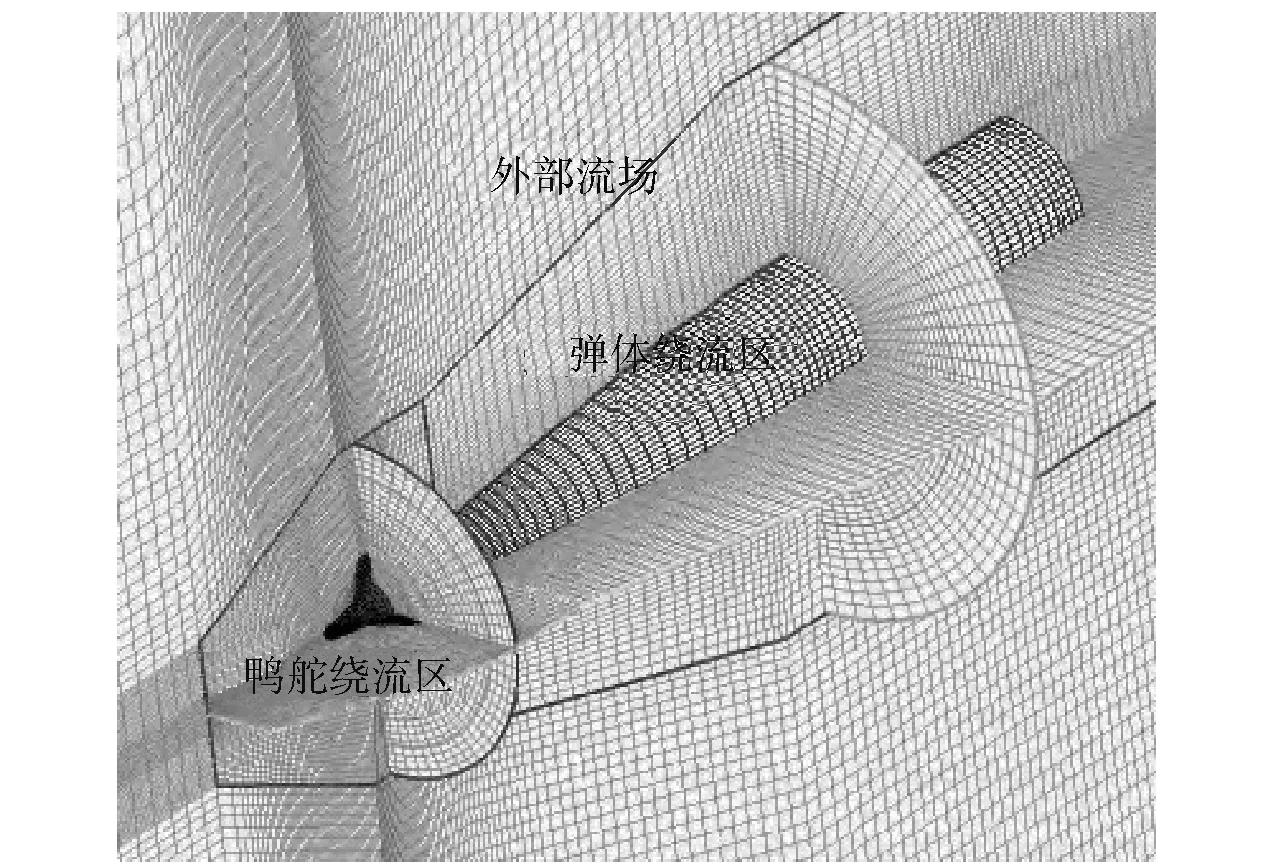
圖4 計算域網格Fig.4 Grid of computational domains

圖5 彈體表面網格Fig.5 Grid of projectile surface

迭代計算中，使用密度基求解器對流項使用Roe通量差分格式離散，梯度使用最小二乘法求解，其他流動變量使用2階迎風格式離散。分別引入Spalart-Allmaras(S-A)湍流模型和剪切壓力傳輸(SST)k-ω湍流模型使控制方程組封閉。流場入口邊界使用壓力遠場條件，出口使用壓力出口，雙旋彈彈體表面使用無滑移壁面條件。計算馬赫數分別為1.5、2.0、2.5、3.0、3.5和4.0，攻角分別為0°、4°時全彈模型受力情況。

數值計算結果和風洞試驗結果的阻力系數、升力系數對比如圖6所示。對于有攻角、無攻角兩種工況下，兩種氣動力系數的計算值和試驗值具有相同變化趨勢。阻力系數計算值與試驗值相對誤差小于13%(見圖6(a))，升力系數計算值相對誤差小于12%(見圖6(b)). 對于工程應用，其相對誤差值處于可接受范圍。通過對比S-A湍流模型和SSTk-ω湍流模型的計算結果可以看出，兩種湍流模型結果高度一致。因此，在數值計算中選擇計算成本較低的單方程S-A湍流模型。

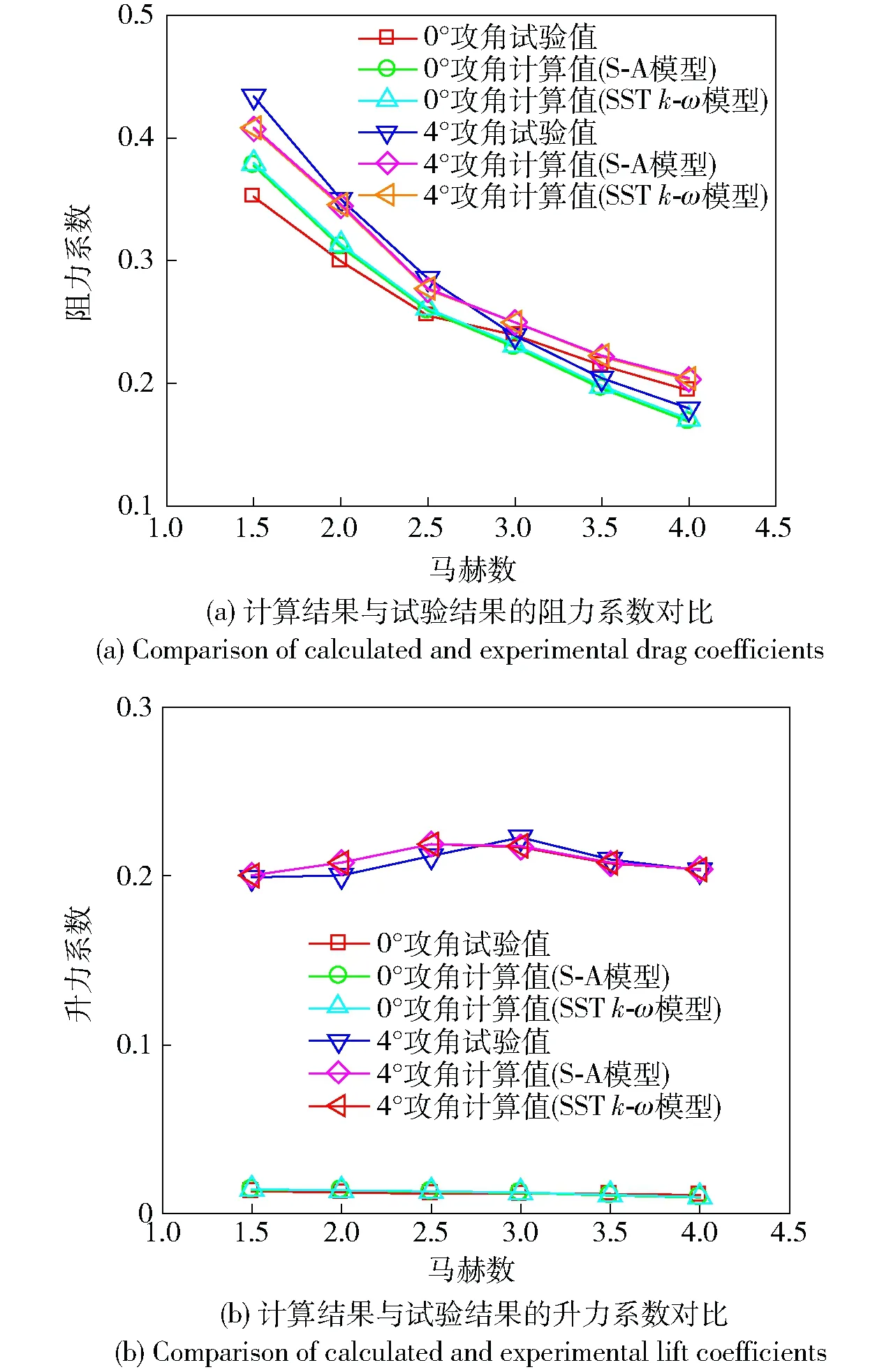
圖6 計算結果與試驗結果的氣動力系數對比Fig.6 Comparison of calculated and experimental aerodynamic coefficients

2 修正力氣動工程模型的建立

固定鴨舵雙旋修正彈通過導引組件轉動來改變修正力方向，從而改變全彈動力平衡角，實現彈道修正。固定鴨舵修正組件產生的修正力來自4片舵片，因此對于4片舵片產生的修正力進行精確建模有助于后續的通用性和修正彈飛行特性研究。

在建立氣動工程模型之前，先建立彈體坐標系，原點O取在全彈質心，x軸與彈軸重合指向彈尾方向，y軸垂直于x軸指向上方，z軸與Oxy平面垂直。根據細長體理論，在小攻角、小舵片偏角、薄彈翼條件下，將固定鴨舵雙旋修正彈導引組件的小擾動流場簡化成由修正彈攻角產生橫向繞流的攻角效應(見圖7(a)，γp為舵片相位角)以及由舵偏角產生的舵偏效應(見圖7(b)，δd為差動舵舵片舵偏角，δm為操作舵舵片舵偏角)兩種效應的疊加。因此，分別單獨考慮任意相位角γp兩種效應的作用，然后將結果線性疊加得到修正力的工程模型。

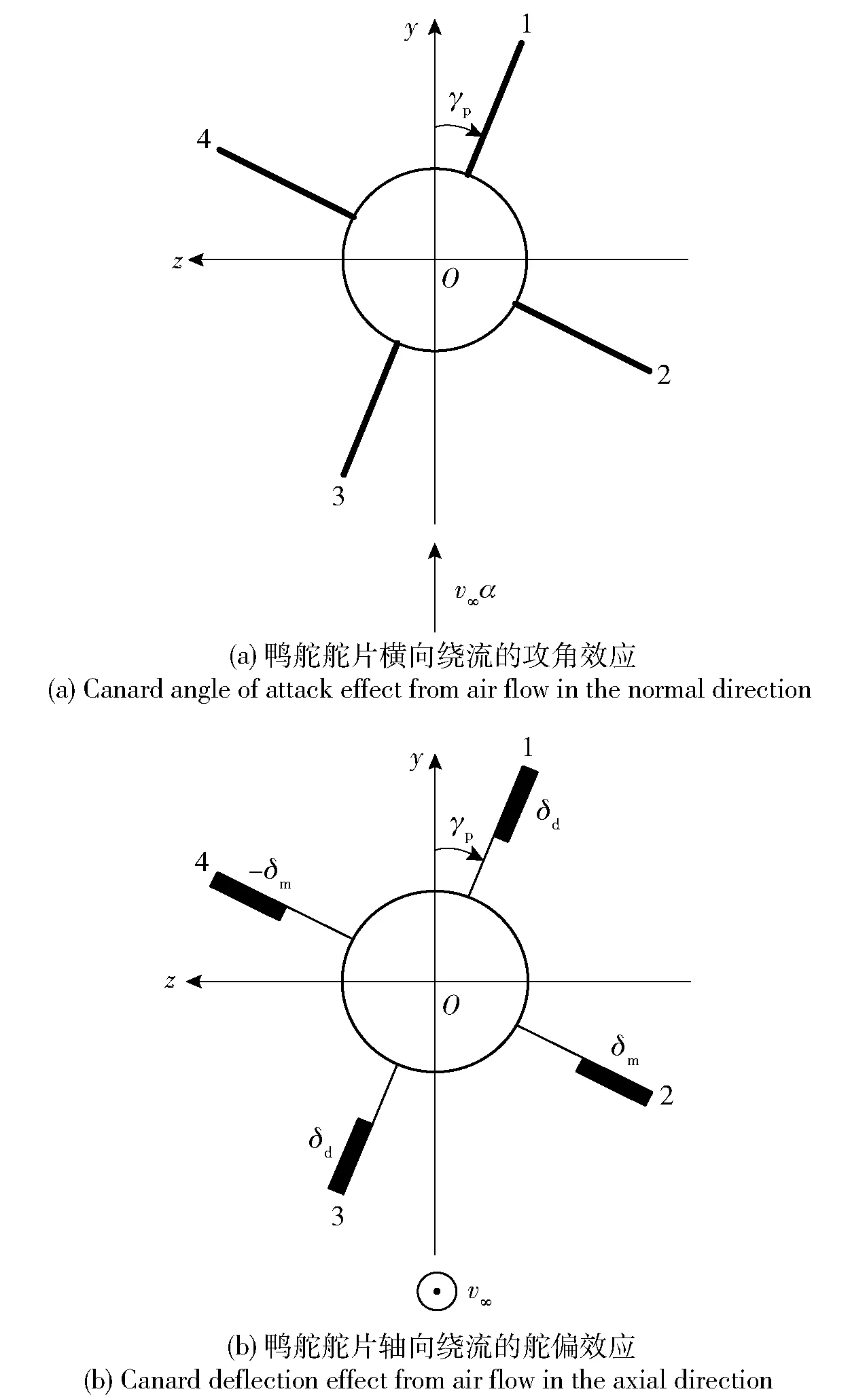
圖7 鴨舵舵片繞流示意圖(彈尾視圖)Fig.7 Air flow in the normal and axial directions (view from the rear of canard)

2.1 攻角效應的修正力

如圖7(a)所示“X”形氣動布局，以舵片1為例，與攻角平面的夾角為γp，設攻角為α，將來流速度分解為平行彈軸速度分量v∞cosα≈v∞和垂直彈軸速度分量v∞sinα≈v∞α. 前者與舵片平面平行，對于薄舵片不產生升力；后者為升力主要來源。v∞α分解為垂直舵片1分量v∞αsinγp和平行舵片1分量v∞αcosγp，前者為舵片1產生法向力主要成因，因此舵片1有效攻角αe=αsinγp. 規定垂直舵片面指向逆時針方向的法向力為正，綜上所述，舵片1由攻角效應產生的法向力表達式為

(1)

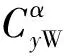
同理，其他3片舵片的法向力表達式依次為

(2)

(3)

(4)

將舵片1所受法向力分解到y軸和z軸方向，得到舵片1產生的y軸方向側向力Fyα1和z軸方向側向力Fzα1如(5)式和(6)式所示：

(5)

(6)

同理，其他3片舵片分解后所得側向力分別為Fyα2、Fzα2、Fyα3、Fzα3、Fyα4、Fzα4.

文獻[9]建立的模型中，攻角效應的修正力為各舵片修正力的直接疊加，并乘以攻角效應下彈頭部對鴨舵舵片升力的干擾系數Kα，其公式如(7)式[9]所示：

(7)

本文綜合考慮導引組件回轉體部分對舵片受力的影響，每片舵片的y軸和z軸方向側向力并不能直接相加，攻角效應的修正力表達式為

(8)

式中：Kα1、Kα2、Kα3、Kα4分別為攻角效應下彈頭部對鴨舵舵片1、舵片2、舵片3、舵片4法向力的干擾系數。(8)式也可寫成以下矩陣形式：

(9)

利用(10)式將氣動力F除以動壓q∞和鴨舵舵片參考面積SW換算為氣動力系數C，

(10)

同理可得到鴨舵舵片攻角效應產生的修正力系數表達式為

(11)

2.2 舵片偏效應的修正力

如圖7(b)所示，只有舵片偏效應中，鴨舵舵片在軸向流的作用下，由舵偏角δd、δm產生法向力。4片舵片法向力表達式分別為

(12)

(13)

(14)

(15)

與2.1節同理，將4片舵片產生的升力在y軸、z軸方向進行分解，得到4片舵片在y軸、z軸方向的修正力分量分別為Fyδ1、Fzδ1、Fyδ2、Fzδ2、Fyδ3、Fzδ3、Fyδ4、Fzδ4.

文獻[9]建立的模型中，舵偏效應的修正力為各舵片修正力的直接疊加，并乘以舵偏角效應下彈頭部對鴨舵舵片升力的干擾系數Kδ，其公式如(16)式[9]所示：

(16)

本文考慮導引組件回轉體部分對舵片受力的影響，舵偏效應修正力的表達式為

(17)

式中：Kδ1、Kδ2、Kδ3、Kδ4分別為舵偏角效應下彈頭部對鴨舵舵片1、舵片2、舵片3、舵片4法向力的干擾系數。

同理，利用(10)式可得舵偏效應產生的修正力系數為

(18)

將由攻角效應產生的修正力與舵偏效應產生的修正力相疊加即可得到導引組件的修正力氣動工程模型：

(19)

(20)

文獻[9]建立氣動模型表達式為

(21)

(21)式仍具有缺陷，如當相位角γp=0°時，z軸方向側向力為0，但是數值計算結果顯示上、下兩片差動舵舵片由于彈體迎風側、背風側的差異，會存在z軸方向側向力，如馬赫數為2.5，攻角為8°，γp=0°時，差動舵舵片產生的z軸方向側向力為-16.71 N. 本文提出的分別考慮4片舵片的修正力模型可以解決這種缺陷。

3 數值計算與參數辨識

建立雙旋彈導引組件修正力氣動工程模型過程中，考慮了彈頭對舵片升力的干擾系數Kα、Kδ. 根據參考文獻[9，11]結論，在給定馬赫數情況下，彈頭對舵片升力的干擾系數只與展徑比有關。對同一馬赫數、不同攻角下的干擾系數進行對比，從而驗證此結論。對馬赫數為1.5和2.5，組件相位角γp不同，攻角α不同時的全彈進行數值計算，獲得組件各舵片的修正力數據，并使用L-M算法對給定馬赫數情況下、不同攻角的干擾系數進行辨識。

3.1 數值計算

由于風洞試驗無法分離出單獨導引組件的受力情況和單獨舵片的受力情況，為了進行參數辨識，本文改為使用CFD方法計算所得數據。

根據氣動工程模型中所需氣動參數，可知數值計算使用模型分為帶有導引組件的修正彈模型(見圖4)和單獨舵片模型(見圖8)兩種。前者用于求解舵片受力，后者用于求解舵片升力線斜率。與第1節相同，迭代計算中使用密度基求解器，對流項使用Roe通量差分格式離散，梯度使用最小二乘法求解，其他流動變量使用2階迎風格式離散。使用S-A湍流模型使控制方程組封閉。流場入口邊界使用壓力遠場條件，出口使用壓力出口，雙旋彈彈體表面使用無滑移壁面條件。計算條件如表1所示。

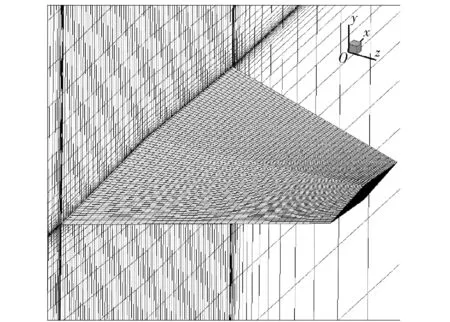
圖8 單獨舵片計算網格Fig.8 Grid of single canard

3.2 參數辨識

使用L-M算法對導引組件修正力氣動模型中頭部對舵片的干擾系數進行辨識。為了驗證給定展徑比情況下，干擾系數只與馬赫數有關，與攻角無關，對馬赫數分別為1.5、2.5，攻角分別為0°、2°、4°和8°時的干擾系數進行辨識。

L-M算法是非線性最小二乘法常用的一種算法，來源于對高斯牛頓法的改進。對于最小二乘問題：

(22)

式中：S(β)為殘差平方和函數；β為待求參數向量；

表1 計算條件

方程f為所建立的模型；xi和yi是第i組已知的變量。

如同高斯牛頓法，方程f(xi，β+Δ)線性近似為

f(xi，β+Δ)≈f(xi，β)+JiΔ，

(23)

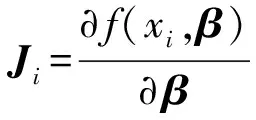
殘差平方和函數S(β)在最小值時，S(β)對β的梯度等于0.

(24)

式中：N為樣本個數。

對于多組已知變量，(24)式可以寫成向量形式：

S(β+Δ)≈‖y-f(β)-JΔ‖2=
[y-f(β)-JΔ]T[y-f(β)-JΔ]=
[y-f(β)]T[y-f(β)]-
2[y-f(β)]TJΔ+ΔTJTJΔ，

(25)

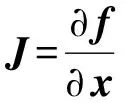
Δ=(JTJ)-1JT[y-f(β)].

(26)

(26)式給出了常規高斯牛頓法迭代增量的表達式。相比于高斯牛頓法，L-M算法引入了阻尼項入，L-M算法迭代增量如(27)式所示：

Δ=(JTJ+λI)-1JT[y-f(β)].

(27)

L-M算法優點在于可以調節：若殘差下降太快，則使用較小的λ，使之更接近高斯牛頓法；若殘差下降太慢，則使用較大的λ，使之更接近梯度下降法。

將本文建立的修正力工程模型寫作矩陣形式：

(28)

f(K)雅克比行列式為

(29)

通過多組迭代計算，對馬赫數分別為1.5、2.5，攻角分別為0°、2°、4°和8°時的干擾系數進行辨識，得到的結果如表2、表3所示。計算表中每列數據的相對極差，結果如表4所示。在給定馬赫數情況下，4片舵片的干擾系數隨攻角相對變化均小于4.9%，因此可以驗證文獻[9，11]結論的正確性。

表3 馬赫數2.5時干擾系數的計算結果

工程模型驗證對比選取在馬赫數分別是為1.5、2.5，攻角為4°情況下，分別使用文獻[9]工程模型、本文工程模型進行修正力計算，與CFD計算所得結果進行對比，對比結果如圖9所示。

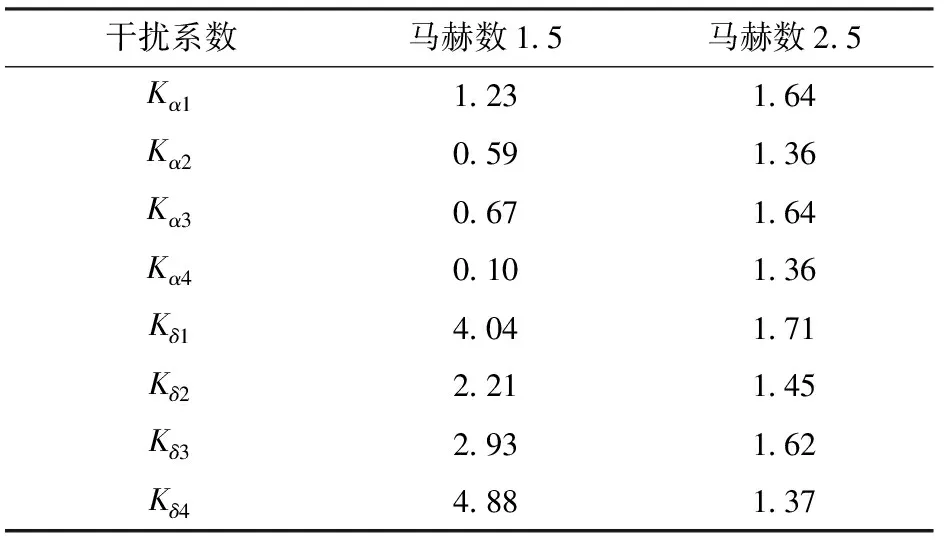
表4 相對極差

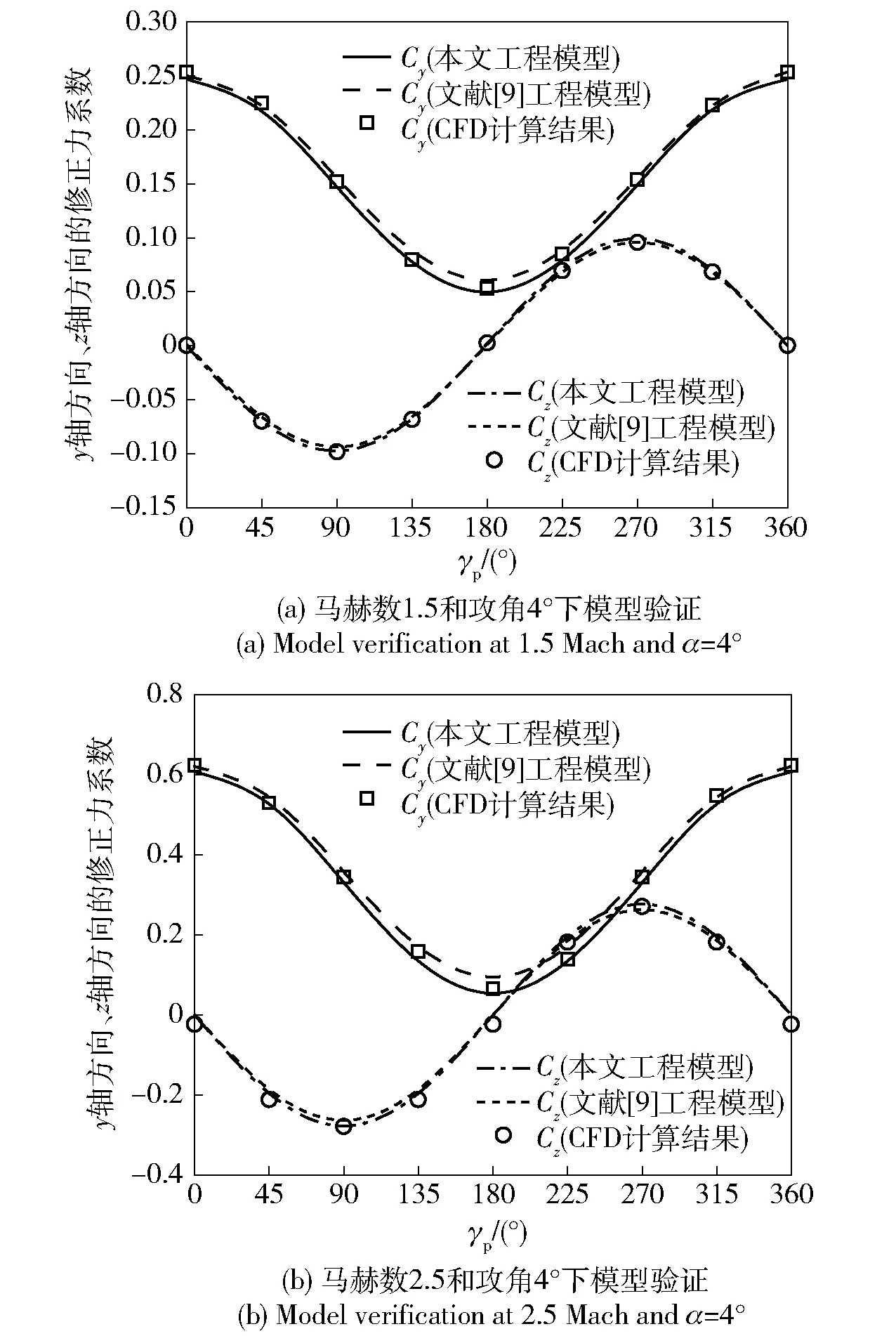
圖9 CFD計算結果對工程模型的驗證Fig.9 Validation of engineering model by CFD results

按照(30)式分別計算CFD計算結果與兩種工程模型在y軸方向、z軸方向的修正力殘差平方和SSR，結果如表5所示。

(30)

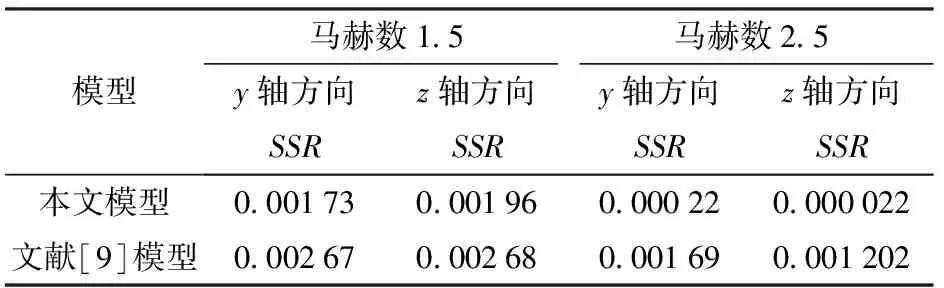
表5 殘差平方和對比

通過對比兩種模型的殘差平方和，可知本文建立的工程模型殘差平方和更小，因此可以認為本文建立的氣動力模型更加符合物理規律。

4 結論

本文使用風洞試驗數據對數值計算方法進行了驗證，基于小擾動理論建立了基于4片舵片的修正力氣動工程模型。依托數值計算結果，通過L-M算法對氣動工程模型中的干擾系數進行辨識，并對模型進行了驗證。根據以上研究得出如下結論：

1)阻力系數計算值與試驗值的相對誤差小于13%，升力系數計算值相對誤差小于12%，數值計算方法有效。

2)本文提出的氣動模型和文獻[9]模型分別與數值計算結果進行驗證擬合，結果(見表5)顯示本文建立模型的殘差平方和更小，因此可以認為本文建立的氣動力模型更加符合物理規律。

3)在同一馬赫數下，不同舵片干擾系數隨攻角相對變化均小于4.9%，驗證了給定馬赫數下彈頭對舵片的干擾系數對攻角變化不敏感。

本文改進后的修正力氣動工程模型更加符合物理規律，頭部修正組件的修正力模型與CFD計算結果吻合較好，對于修正彈的進一步飛行特性研究具有重要意義。