激光光路控制電磁作動器的模糊PID控制特性分析

孫鳳， 張琪， 徐方超， 李強， 金俊杰， 佟玲， 張曉友， 劉巍巍

(沈陽工業大學 機械工程學院， 遼寧 沈陽 110870)

0 引言

激光在工業領域中主要被應用于切割、焊接、3D打印、標記和熱處理等領域[1]。傳統激光切割過程中，輔助氣體噴射中軸線始終與激光焦點中軸線同軸，Quintero等[2]通過實驗驗證了改變輔助氣體噴射中軸線與激光焦點中軸線角度可以提高切割效率與切口質量。從空氣動力學角度分析，不改變輔助氣體噴射中軸線與激光焦點中軸線角度，只改變二者相對位置，即輔助氣體噴射中軸線與激光焦點中軸線不同軸也能達到提高加工工件質量和加工速度的目的。但這需要一種結構緊湊、響應速度快的作動器來實現激光焦點中軸線位置的實時控制。

傳統驅動平臺由于體積大、響應速度慢、噪聲大等缺點，以致很難達到理想的控制精度。磁懸浮技術因具有無接觸、無摩擦、無磨損、不需要密封和潤滑等優點，被應用于定位精度高、響應速度快的驅動領域[3-5]。Molenaar 等[6]設計了一種TU型6自由度磁懸浮定位平臺，U型結構作為定子，T型結構纏有線圈作為動子在U型結構內運動產生水平推力，懸浮力由定子上3個懸浮線圈產生。陳本永等[7]設計了一種磁懸浮微動平臺，建立了電磁驅動數學模型，并運用MATLAB軟件進行了運動特性分析，為磁懸浮微動平臺的設計和研究提供了理論基礎。李群明等[8]根據設計好的磁懸浮平臺，建立了系統動力學方程和機電耦合動力學模型，并根據機電耦合動力學模型對平臺穩定性進行了分析，得到了平臺穩定時懸浮控制的參數范圍，從而證明了采用磁懸浮技術控制平臺具有良好的動態性能和靜態性能。

為了實時控制輔助氣體噴射中軸線與激光焦點中軸線的相對位置，本文設計了一種結構緊湊、響應速度快、無需潤滑的電磁作動器。若采用傳統PID控制算法，由于電磁作動器電磁力是電流和氣隙的非線性函數，難以建立起精確的數學模型。而采用模糊PID控制算法無需建立精確的數學模型，并且可以獲得較好動態性能[9-11]。結合電磁作動器和模糊PID控制算法的優點[12-16]，本文設計了一種模糊PID控制的電磁作動永磁復位式3自由度電磁作動器。

1 電磁作動器結構與數學模型

1.1 電磁作動器結構

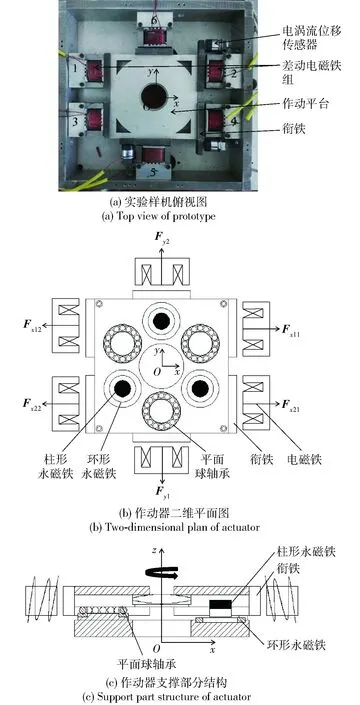
圖1 電磁作動器實驗的作動平臺Fig.1 Experimental prototype of electromagnetic actuator

電磁作動器作動平臺結構如圖1所示。圖1(a)為3對差動電磁鐵的差動結構布置。圖1(b)為電磁作動器二維平面圖，包括圓柱形永磁鐵、環形永磁體、平面球軸承、電磁鐵和銜鐵，其中Fx11、Fx12、Fx21、Fx22分別為作動平臺運動過程中x軸方向2對差動電磁鐵電磁力，Fy1、Fy2分別為y軸方向1對差動電磁鐵電磁力。圖1(c)為電磁作動器支撐部分結構，由平面球軸承、環形永磁鐵和圓柱形永磁鐵組成。其中，軸線同心、同極相對的軸向磁化環形永磁體和圓柱形永磁體組成的永磁彈簧結構為3組，與平面球軸承均勻分布。每組永磁彈簧在z軸方向上表現為吸引力，在x軸和y軸方向上表現為排斥力，從而可以保證電磁鐵斷電時，在x軸和y軸方向上平臺可以自動回復到初始位置。

1.2 電磁作動器作動平臺數學模型

如圖2所示：根據作動平臺結構，選取初始位置質心O(x，y，θ)為坐標原點，其中，θ為作動平臺繞質心轉動的角度；作動平臺運動過程中，圓柱形永磁體和環形永磁體之間回復力分別為Fm1、Fm2、Fm3，平面球軸承與作動平臺上頂蓋之間摩擦力為f. 電磁鐵電磁力、圓柱形永磁鐵和環形永磁鐵之間回復力及平面球軸承與作動平臺上頂蓋之間摩擦力共同作用，使得作動平臺做Oxy平面內的平動和繞作動平臺質心的轉動，作動平臺質心偏離到O′(x1，x2，y)位置。根據作動平臺結構、物理參數和力學特性，令位移傳感器與銜鐵之間氣隙相對增大方向為正，作動平臺繞質心逆時針旋轉方向為正。

圖2 電磁作動器受力分析圖Fig.2 Force analysis chart of electromagnetic actuator

設初始質心O廣義坐標為

(1)

作動平臺3對電磁鐵和3個位移傳感器廣義坐標為

(2)

兩坐標之間的變換關系為

(3)

式中：x1為圖1(a)電磁鐵2上方位移傳感器檢測到的數值；x2為圖1(a)電磁鐵4下方位移傳感器檢測到的數值；L為電磁鐵2和電磁鐵4兩側位移傳感器之間的距離。

1對差動電磁鐵驅動力[17]為

Fx1=kii+kxx，

(4)

式中：ki和kx分別為電流剛度系數和x軸方向位移剛度系數；i為差動電磁鐵中的電流值。

經過仿真分析和實驗驗證，圓柱形永磁體和環形永磁體組成的永磁彈簧結構徑向磁力與徑向位移之間關系如圖3所示。當徑向位移較小時，永磁彈簧結構徑向磁力隨著徑向位移的增加而增加，所產生徑向回復力與徑向位移可近似看作線性關系，即

Fm=ktδ，

(5)

式中：Fm為1對圓柱形永磁體與圓環形永磁體之間的徑向回復力；kt為磁彈簧剛度系數；δ為徑向位移。

圖3 徑向磁力與徑向位移關系Fig.3 Relationship between radial magnetic force and radial displacement

系統運動方程為

(6)

根據系統動力學方程建立系統狀態空間方程為

(7)

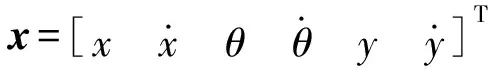
作動平臺結構參數如表1所示。

表1 作動平臺結構參數

2 模糊PID控制器設計

2.1 論域和隸屬函數設計

模糊PID控制器被控對象無需建立精確數學模型，在傳統PID控制器基礎上，以位置偏差e和位置偏差變化率ec作為模糊PID控制器輸入，采用模糊推理方法對PID參數kP、kI、kD進行調節，來滿足不同e和ec對控制系統的要求，從而使被控系統具有良好的動態性能和靜態性能。根據電磁作動器特點，本文模糊PID控制器以e和ec作為控制器輸入，PID參數變化量ΔkP、ΔkI、ΔkD作為控制器輸出，結合作動平臺利用模糊規則對PID參數進行在線調整，如圖4所示。

圖4 模糊PID控制器結構圖Fig.4 Structure diagram of fuzzy PID controller

根據作動平臺實際情況，本文模糊PID控制器采用均勻的三角形隸屬度函數，并用Mamdani方法進行模糊推理。采用重心法對模糊推理所得位移進行模糊判決，從而得到位移精確值，再乘以比例因子輸出位移實際值。將實際值與反饋位移比較得到作動平臺的e，將e和ec輸入到參數自校正模糊PID控制器中，在線運行過程中，控制系統通過對模糊規則的查表和運算，完成對PID參數的在線自校正。

模糊PID控制器輸入e、ec和輸出ΔkP、ΔkI、ΔkD的模糊子集定義分別為

e=ec={NB NM NS ZO PS PM PB}，
ΔkP=ΔkI=ΔkD={NB NM NS ZO PS PM PB}，

式中：NB、NM、NS、ZO、PS、PM、PB分別為負大、負中、負小、0、正小、正中、正大；模糊控制器e、ec的實際變化范圍稱為其基本論域，e和ec的論域為(-6，6)，ΔkP、ΔkI、ΔkD的論域為(-6，6).

2.2 量化因子、比例因子的確定

在進行模糊化運算時，需要將e、ec等變量的基本論域轉化為相應模糊論域，因此需要引入量化因子。同理，在經過模糊PID控制器處理后，需要將處理后變化量的模糊論域變成實際控制對象的基本論域，中間需要一個比例因子。而量化因子和比例因子的選擇與PID參數、作動平臺的動態性能有關，作動平臺輸入e的基本論域為[-3,3]，模糊論域為[-6,6]，則其量化因子為6/3=2. 同理，根據作動平臺特性，輸入ec量化因子取值為0.01，輸出ΔkP、ΔkI、ΔkD比例因子取值分別為5、20、0.000 6.

2.3 模糊規則的確定

調節前期，e較大時，為了使作動平臺獲得較快響應速度，取較大kP，由于開始時e有可能瞬時變大而導致微分過飽和，使控制作用超出控制范圍。為防止銜鐵被電磁鐵吸引，應取較小kD，同時為了防止出現較大超調，產生積分飽和，應對積分作用加以限制，一般取kI=0. 當e和ec處于中等大小時，為了使系統具有較小超調，kP取值應適中；為了避免影響穩定性，kI取值應適中；這時kD取值對系統控制特性影響比較敏感，kD取值應適當減小。

當e較小、快接近給定值時，為了使系統具有較好穩定性能，應減小kP取值來減少靜差，抑制超調，同時應適當增加kI取值。為了在給定值附近出現振蕩現象，并考慮系統抗干擾性能，這時kD取值非常重要。一般來說，當ec較小時，kD取值應大一些；當ec較大時，kD取值可小一些。根據上述規律和實際操作經驗，可制定出針對PID參數ΔkP、ΔkI、ΔkD模糊控制規則，如表2所示。

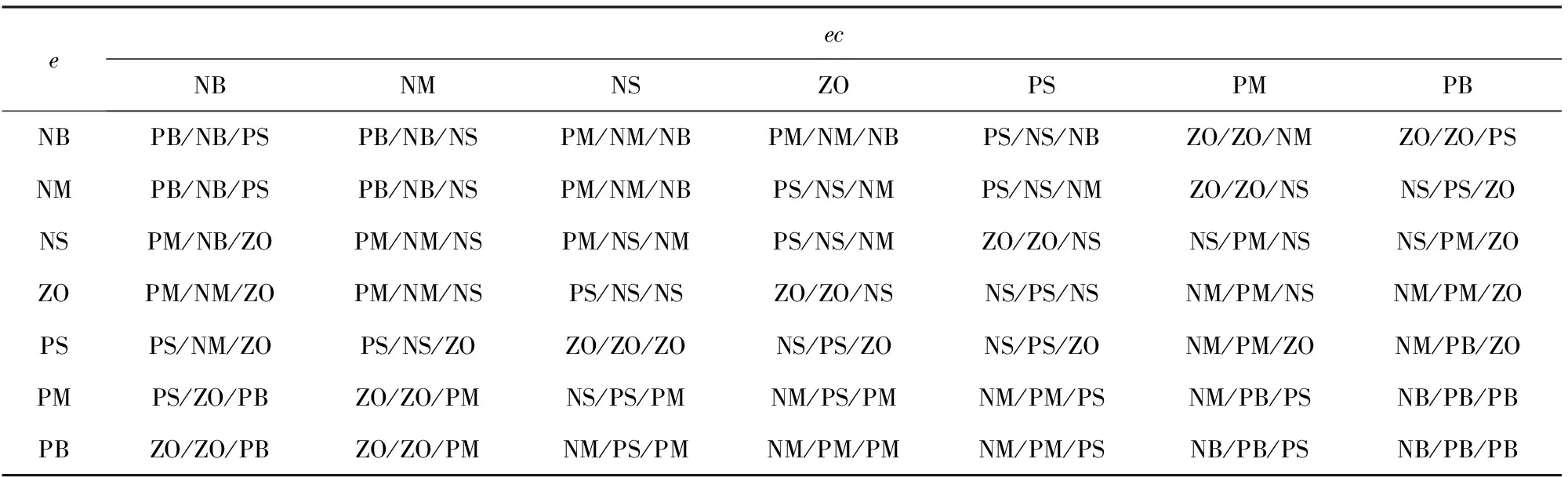
表2 參數ΔkP、ΔkI、ΔkD控制規則調整表

3 仿真分析

激光切割機焦點控制系統的電磁作動器整體控制框圖如圖5所示。電磁鐵1與電磁鐵2，電磁鐵3與電磁鐵4，電磁鐵5與電磁鐵6分別構成3對差動電磁鐵，其中，電磁鐵1與電磁鐵2，電磁鐵3與電磁鐵4一起控制作動平臺x軸方向平動和繞質心轉動，電磁鐵5與電磁鐵6控制作動平臺y軸方向平動。首先電渦流位移傳感器將測量到的位移信號傳給該系統核心處理器dSPACE1103，通過 Controldesk與MATLAB/Simulink連接，得到偏差信號作為模糊PID控制器的一個輸入，控制功率放大器中的電流大小，并實現對每對差動電磁鐵的實時控制。根據模糊PID控制器結構和原理，選擇在MATLAB/Simulink環境下分別對x軸方向、y軸方向進行仿真。

圖5 系統控制結構圖Fig.5 Control structure diagram of the proposed system

3.1 傳統PID控制器x軸方向位置響應仿真分析

根據作動平臺建立數學模型，參考線性二次型調節器(LQR)最優控制策略，通過試湊法進行調節，最終得到相對最優控制參數。傳統PID控制器參數kP、kI、kD取值分別為2 754、10 000、10時，傳統PID控制器x軸方向位置響應仿真結果如圖6所示。

由圖6可見，0.20 s時，給作動平臺x軸方向一個0.10 mm位移階躍信號，作動平臺向左運動并在0.35 s保持穩定。作動平臺響應時間為0.15 s，作動平臺位置由0 mm到0.13 mm最后穩定在0.10 mm，由此可知，傳統PID控制器x軸方向平動最大超調量為30%.由于作動平臺為平動，控制電流都是從0 A開始先增加最后趨于穩定。從中可以看出，傳統PID控制器可以使作動平臺在x軸方向實現穩定控制。

3.2 模糊PID控制器x軸方向位置響應仿真分析

根據作動平臺參數和LQR控制策略，通過試湊法進行調節，最終得到相對最優控制參數。模糊PID控制器參數kP、kI、kD取值分別為2 754、10 000、10，量化因子取值分別為2、0.01，比例因子取值分別為5、20、0.000 6時，模糊PID控制器x軸方向位置響應仿真結果如圖7所示。

圖7 模糊PID控制器x軸方向仿真結果Fig.7 Simulated results of fuzzy PID controller in x-axial direction

由圖7可見，0.20 s時，給作動平臺x軸方向一個0.10 mm位移階躍信號，作動平臺向左運動。作動平臺響應時間為0.15 s，作動平臺位置由0 mm最后到0.10 mm，最大位置在0.13 mm，模糊PID控制器平動x軸方向位置響應超調量為30%. 由于作動平臺是平動，控制電流變化趨勢是相同的。從中可以看出，模糊PID控制器可以使作動平臺在x軸方向實現穩定控制。

3.3 傳統PID控制器y軸方向位置響應仿真分析

根據作動平臺建立數學模型，參考LQR控制策略，通過試湊法進行調節，最終得到相對最優控制參數。將傳統PID控制器參數kP、kI、kD分別取10、22 000、0.01，y軸方向傳統PID控制器仿真結果如圖8所示。0.20 s時，給作動平臺y軸方向一個0.10 mm位移階躍信號，作動平臺向上運動。作動平臺響應時間為0.60 s，位移最大變化量為0.11 mm，位移響應最大超調量為10%，控制電流由0 A變化到0.30 A最后趨于0 A穩定。從中可以看出，傳統PID控制器可以使作動平臺在y軸方向實現穩定控制。

圖8 傳統PID控制器y軸方向仿真結果Fig.8 Simulated results of traditional PID controller in y-axial direction

3.4 模糊PID控制器y軸方向位置響應仿真分析

圖9 模糊PID控制器y軸方向仿真結果Fig.9 Simulated results of fuzzy PID controller in y-axial direction

根據作動平臺參數和LQR控制策略，通過試湊法進行調節，最終得到相對最優控制參數。模糊PID控制器參數kP、kI、kD取值分別為10、22 000、0.01，量化因子取值分別為2、0.01，比例因子取值分別為5、20、0.000 6. 模糊PID控制器y軸方向仿真結果如圖9所示。0.02 s時，給作動平臺y軸方向一個0.10 mm位移階躍信號，作動平臺向上運動，并在0.14 s時穩定。作動平臺響應時間為0.12 s，位置最大變化量為0.10 mm，系統無超調。控制電流由0 A到0.40 A再到0 A趨于穩定。與傳統PID控制器相比，模糊PID控制器響應時間減少了0.48 s，超調量減少了10%，模糊PID控制器可以使作動平臺在y軸方向實現穩定控制，并且對超調量和響應速度的控制效果更好。

4 實驗分析

磁力作動器實驗裝置包括作動平臺、控制器dSPACE1103、電渦流位移傳感器、E120/06功率放大器。經過反復調試實驗裝置后，分別對x軸方向、y軸方向平動進行響應特性分析。作動平臺控制部件如圖10所示。

圖10 作動平臺控制部件Fig.10 Control components of experimental platform

首先分別給x軸方向2對電磁鐵組、y軸方向1對電磁鐵組接通1.20 A的偏置電流，使設定值與位移傳感器檢測數值相等，將經過控制器放大處理后的控制電流與電磁鐵組中的偏置電流進行相加、減，構成差動電磁鐵組對作動平臺進行控制。

4.1 傳統PID控制器x軸方向位置響應分析

傳統PID控制器參數kP、kI、kD取值分別為2 754、10 000、10時，對作動平臺x軸方向平動進行控制。傳統PID控制器x軸方向平動位置響應結果如圖11所示。

圖11 傳統PID控制器x軸方向實驗結果Fig.11 Experimental results of traditional PID controller in x-axial direction

由圖11可見，2.00 s時，給作動平臺x軸方向一個0.10 mm位移階躍信號，作動平臺向左運動。作動平臺位置響應在4.00 s時趨于穩定，作動平臺響應時間為2.00 s，作動平臺位置由2.28 mm到2.38 mm，系統無超調。線圈1電流由1.30 A上升到1.50 A，線圈3電流由0.80 A上升到1.50 A，線圈2電流由1.10 A下降到0.85 A，線圈4電流由1.60 A下降到0.90 A，上方差動電磁鐵控制電流由0.20 A上升到0.50 A，下方差動電磁鐵控制電流由-0.65 A上升到0.50 A. 線圈1、線圈3電流增加，則電磁鐵1、電磁鐵3電磁力增加；而線圈2、線圈4電流減小，則電磁鐵2、電磁鐵4電磁力減小。作動平臺向左移動，2組差動電磁鐵的控制電流變化趨勢都是增加的。

4.2 模糊PID控制器x軸方向位置響應分析

模糊PID控制器參數kP、kI、kD取值分別為2 754、10 000、10，量化因子取值分別為2、0.01，比例因子取值分別為5、20、0.000 6時，對作動平臺x軸方向平動進行控制，模糊PID控制器x軸方向平動位置響應結果如圖12所示。

圖12 模糊PID控制器x軸方向實驗結果Fig.12 Experimental results of fuzzy PID controller in x-axial direction

由圖12可見，2.60 s時，給作動平臺x軸方向一個0.10 mm位移階躍信號，作動平臺向左移動。作動平臺位置響應在3.10 s時逐漸趨于穩定，作動平臺響應時間為0.50 s，作動平臺位置由1.53 mm到1.63 mm，系統無超調。線圈1電流由1.20 A上升到1.80 A，線圈3電流由1.00 A上升到1.40 A最后穩定在1.30 A，線圈2電流由1.15 A下降到0.65 A，線圈4電流由1.40 A下降到1.00 A最后穩定在1.10 A，上方差動電磁鐵控制電流由0 A上升到1.00 A，下方差動電磁鐵控制電流由-0.50 A上升到0.40 A最后穩定在0.20 A.線圈1、線圈3電流增加，則電磁鐵1、電磁鐵3電磁力變大；而線圈2、線圈4電流減小，則電磁鐵2、電磁鐵4電磁力變小。作動平臺向左運動并在3.10 s時穩定，與傳統PID控制器對比，模糊PID控制器作動平臺位置響應時間減少了1.50 s，響應時間變短，響應速度更快。

4.3 傳統PID控制器y軸方向響應特性分析

傳統PID控制器參數kP、kI、kD取值分別為10、22 000、0.01時，對作動平臺y軸方向進行控制，傳統PID控制器y軸方向位置響應結果如圖13所示。

由圖13可見，1.70 s時，給作動平臺y軸方向一個0.10 mm位移階躍信號，作動平臺向上移動。作動平臺位移響應在4.00 s時穩定，響應時間為2.30 s，作動平臺位置由2.86 mm到2.97 mm，系統無超調。線圈5電流由0.75 A上升到2.20 A，線圈6電流由1.60 A下降到0.35 A，控制電流由-0.70 A上升到1.50 A. 由于控制電流變大，線圈5電流變大，線圈6電流變小，直接導致電磁鐵5電磁力變大，電磁鐵6電流變小，作動平臺上移，最后穩定在新的平衡位置。從中可以看出，傳統PID控制器可以使作動平臺在y軸方向實現穩定控制。

4.4 模糊PID控制器y軸方向響應特性分析

模糊PID控制器參數kP、kI、kD取值分別為10、22 000、0.01，量化因子取值分別為2、0.01，比例因子取值分別為5、20、0.000 6時，對作動平臺y軸方向進行控制，如圖14所示為模糊PID控制器y軸方向位置響應結果。

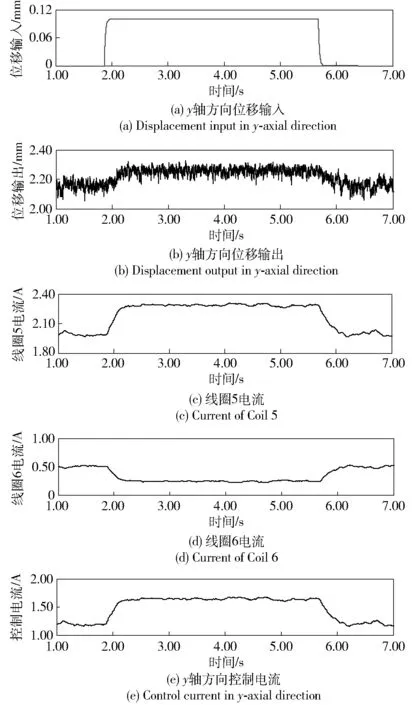
圖14 模糊PID控制器y軸方向實驗結果Fig.14 Experimental results of fuzzy PID controller in y-axial direction

由圖14可見，1.88 s時，給作動平臺y軸方向一個0.10 mm位移階躍信號，作動平臺向上運動且響應速度更快，在2.30 s時穩定，其響應時間為0.42 s. 作動平臺位置由2.15 mm到2.25 mm，系統無超調。線圈5電流由2.00 A上升到2.30 A，線圈6電流由0.50 A下降到0.25 A，控制電流由1.20 A上升到1.65 A. 與傳統PID控制器相比，模糊PID控制器位置響應時間縮短1.88 s，系統無超調。從中可以看出，模糊PID控制器可以使作動平臺在y軸方向具有較好位移響應特性，并且控制效果要好于傳統PID控制器。

5 模糊PID控制參數優化實驗

模糊PID控制器參數kP、kI、kD取值分別為2 754、10 000、10，量化因子取值分別為2、0.01，比例因子取值分別為5、20、0.000 6時，對作動平臺x軸方向平動進行控制。由于x軸方向和y軸方向電磁鐵之間耦合和摩擦力的影響，作動平臺響應效果不太理想。經過對模糊PID控制器參數反復試湊，當模糊PID控制器參數kP、kI、kD取值分別為15、150 000、10，量化因子取值分別為2、0.01，比例因子取值分別為5、20、0.000 6時，對作動平臺x軸方向平動進行控制，如圖15所示為模糊PID控制器x軸方向平動位置響應結果。

圖15 模糊PID控制器參數優化后x軸方向實驗結果Fig.15 Experimental results with optimized fuzzy PID controller in x-axial direction

由圖15可知，2.25 s時，給作動平臺x軸方向一個0.10 mm位移階躍信號，作動平臺位置響應在2.35 s時逐漸趨于穩定，作動平臺響應時間為0.10 s. 作動平臺位置由2.11 mm到2.21 mm，系統超調為0.9%. 線圈1電流由1.05 A上升到1.35 A，線圈3電流由1.60 A上升到1.85 A最后穩定在1.75 A，線圈2電流由1.30 A下降到1.00 A，線圈4電流由0.75 A下降到0.52 A最后穩定在0.65 A，上方差動電磁鐵控制電流由-0.20 A上升到0.30 A，下方差動電磁鐵控制電流由0.70 A增加到1.15 A最后穩定在0.95 A. 線圈1、線圈3電流增加，則電磁鐵1、電磁鐵3電磁力增加；而線圈2、線圈4電流減小，則電磁鐵2、電磁鐵4電磁力減小。作動平臺向左運動并在2.35 s時保持穩定，模糊PID控制器位置響應控制效果較好。

6 結論

1)作動平臺在x軸方向位置響應仿真實驗中，傳統PID控制器和模糊PID控制器二者控制效果基本相同。作動平臺在y軸方向位置響應仿真實驗中，模糊PID控制器響應時間較傳統PID控制器響應時間縮短0.48 s，超調量減少10%.

2)x軸方向模糊PID控制器參數kP、kI、kD取值分別為2 754、10 000、10，量化因子取值分別為2、0.01，比例因子取值分別為5、20、0.000 6；y軸方向模糊PID控制器參數kP、kI、kD取值分別為10、22 000、0.01，量化因子取值分別為2、0.01，比例因子取值分別為5、20、0.000 6. 該情況下的位置響應實驗結果說明，與傳統PID控制器相比，模糊PID控制器x軸方向位置響應時間提高了1.50 s，在y軸方向位置響應時間縮短了1.88 s. 在切割速度低、精度要求不高的低速切割中，可用此模糊PID控制器參數進行切割。

3)模糊PID控制器參數kP、kI、kD取值分別為15、150 000、10，量化因子取值分別為2、0.01，比例因子取值分別為5、20、0.000 6情況下，x軸方向優化實驗中，作動平臺響應時間提高到0.10 s，此優化參數可用于切割速度快、精度要求高的高速切割。