基于響應面法全液壓濕式驅動橋殼可靠性優化

周軍超， 杜子學， 王 潔， 廖映華

(1. 四川理工學院 機械工程學院，四川 自貢 643000； 2. 重慶交通大學 軌道交通研究院，重慶 400074；3. 過程裝備與控制工程四川省高校重點實驗室，四川 自貢 643000)

0 引 言

全液壓濕式驅動橋多應用在裝載機等工程機械[1]。驅動橋殼作為全液壓式驅動橋重要部件，主要作用是支撐并保護主減速器、差速器和半軸等，并支承車架及其以上各總成質量[2]。SHAO Yimin等[3]、劉為等[4]、GAO Jing等[5]、周軍超等[6]和YU Xianzhong等[4]分別采用有限元方法對橋殼進行優化設計，對不同工況下橋殼的應力應變進行分析。郭冬青等[8]利用有限元分析技術對驅動橋試驗模型和靜力學進行了分析和優化。孫忠云等[9]基于靜疲勞、靜載荷、側傾強度、緊急制動等條件約束，研究了某驅動橋可靠性優化模型，其結果表明優化效果明顯。呂國坤等[10]提出基于二次響應曲面法進行優化設計，確定襯環為距橋殼片外端部時響應優化模型，通過對比橋殼改進前后的有限元分析得出加襯環后驅動橋殼應力明顯降低，安全系數提高顯著，并通過臺架試驗驗證了改進措施的正確性和有效性。傳統優化設計忽略了驅動橋結構參數的不確定性，其最優解只是數學意義的最優解，而實際工作時橋殼不但受到確定性因素影響，還受到諸如邊界條件、尺寸波動等不確定性影響。因此對橋殼在確定性優化基礎上進行可靠性優化具有重要意義。

響應面法(response surface methodology,RSM)在全局收斂性及優化效率上具有較強優勢[11]，近年來已成為熱門的優化方法。不少學者將響應面法應用到結構固有頻率優化設計中[12]和應用響應面進行結構多目標分析與設計中[13]。比如：路懷華等[14-16]針對轉向系結構參數不確定性，將可靠性與響應面結合，對汽車轉向系統固有頻率進行了優化。

筆者以全液壓濕式驅動橋殼為優化目標，為提高驅動橋殼系統優化設計效率和可靠性，減少計算量，采用相應面方法和可靠性技術相結合對橋殼進行優化。首先建立驅動橋殼的有限元模型，通過有限元分析選擇輪邊板簧座附近，選取此處截面的形狀作為優化目標函數，再進行拉丁試驗設計，用二階多項式獲取橋殼的響應面近似優化模型，最后基于相應面模型進行驅動橋殼的可靠性優化設計，得到優化后橋殼的參數值與設計點。

1 橋殼有限元分析

筆者在CATIA中建立驅動橋橋殼模型，對有限模型進行處理。將圖紙中出現的諸如倒角、圓角等細小特征盡量采取簡化措施，最后橋殼模型如圖1。將三維模型導入ANSYS軟件后進行網格劃分[6]，橋殼網格劃分使用單元類型為SOLID185。該單元通過8個節點來定義，具有超彈性、應力剛化、蠕變、大變形和大應變能力等特點。有限元模型如下圖2，共有331 201單元，166 923節點。

圖1 橋殼模型Fig. 1 Axle housing model

圖2 橋殼有限元模型Fig. 2 Finite element model of axle housing model

車橋模型單橋滿載為7t，其整橋參數詳見表1。

表1 車橋參數Table 1 Specific parameters of the axle

橋殼本體材料使用QT600-3，彈性模量為E=1.69×1011Pa，泊松比為μ=0.286。動載系數為3.5，安全系數為1.5。

對整體式橋殼進行滿載不平路面行駛、車輪承受最大切向力、車輪承受最大側向力等3種工況下的有限元分析，分析過程見文獻[6]，分析結果如圖3。從圖3可看出：這3種工況下橋殼最大應力應變出現在輪邊截面板簧座附近，選取此處截面形狀作為優化目標函數。

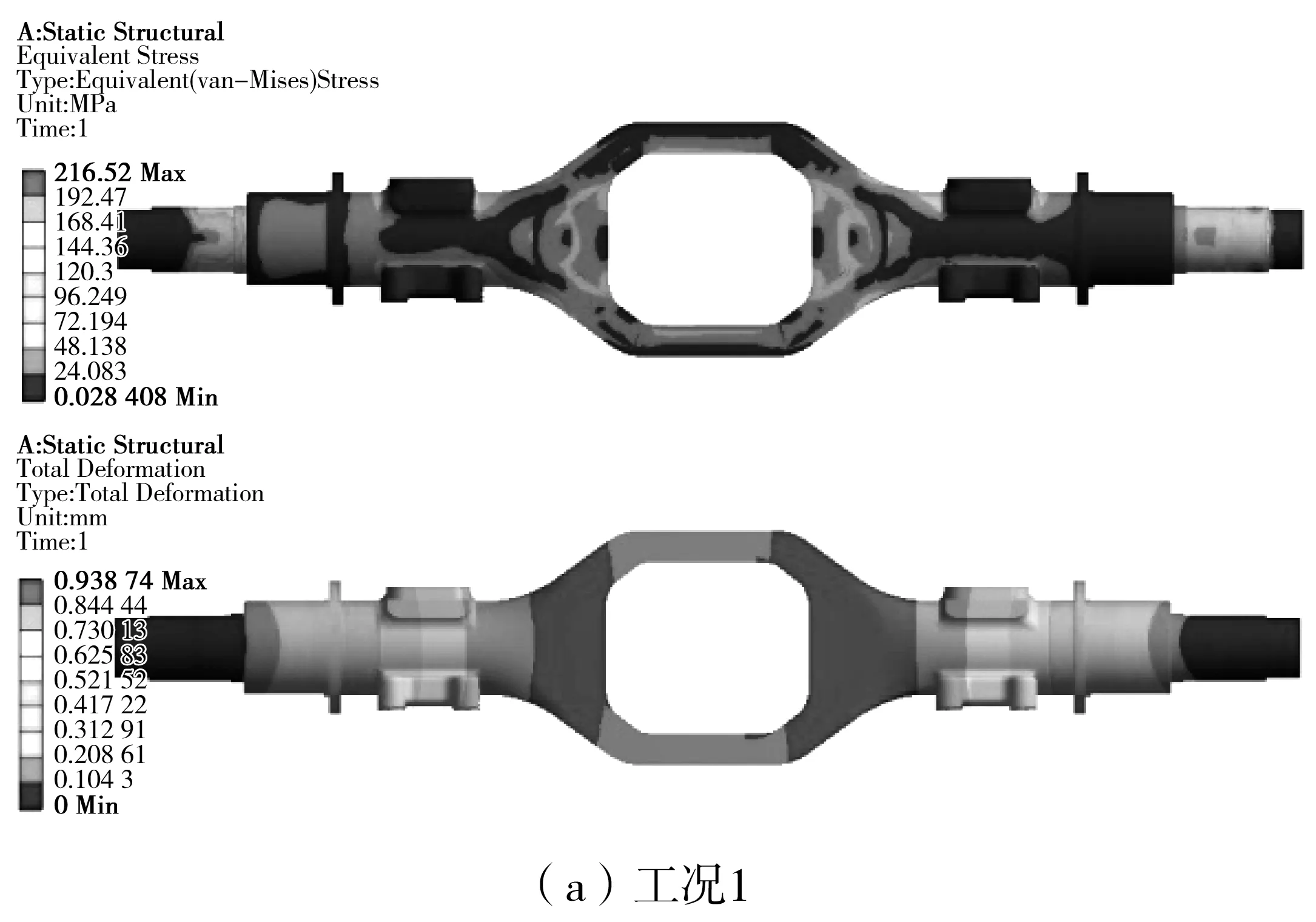
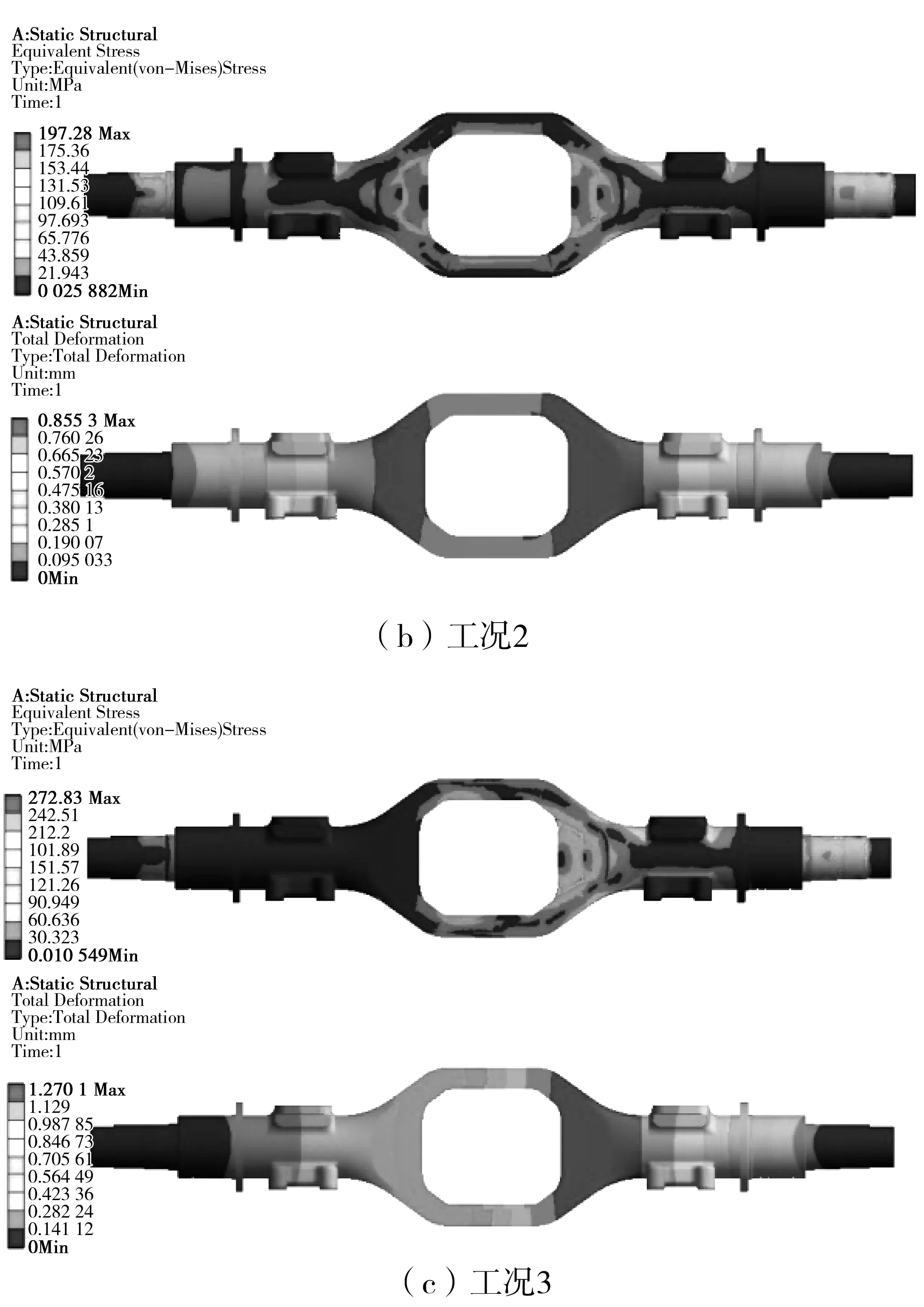
圖3 3種工況下橋殼應力變形Fig. 3 Stress deformation of the axle housing under 3 working conditions

2 響應面法

響應面法基本原理是通過構造一個具有明確表達形式的多項式來表達隱式功能的函數[12]。用這個表達式代替實際函數進行復雜運算，因此可快速提高產品結構分析計算和優化設計。響應面法的在工程優化設計中，不僅可得到響應目標與設計變量之間的變化關系，而且可得到優化方案，即設計變量的最優組合，使目標函數達到最優。

假設系統響應Y與設計變量之間關系如式(1)：

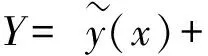
(1)

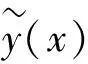
根據工程經驗，響應面函數近似二項式表達式如式(2)[9]：

(2)

式中：β為未知系數；k為設計變量的數量；Y為預測響應值；β0為偏移項；βi為線性偏移；βii為二階偏移系數；βij為交互作用系數。

3 驅動橋殼可靠性優化

可靠性設計原理是將設計變量(如載荷、應力等)視為一定分布規律的隨機性變量，用概率方法進行產品可靠性設計[14]。可靠性設計是給定各個設計變量的概率分布函數，將各個確定的設計轉化為概率約束。以確定性優化解為均值，取均方差與均值之比為0.01，采用基于響應面法可靠性優化計算。驅動橋殼可靠性優化數學模型如式(3)：

(3)

式中：F為響應面目標函數；P(t,X)為約束函數；R0為可靠度目標；hi(x)為約束條件。

當f(x)>0時，此時結構可靠度Rs如式(4)：

(4)

式中：f(x)為狀態函數。

基于響應面法的汽車橋殼可靠性優化步驟如下：

步驟1：確定設計變量及設計目標。通過對驅動橋殼CAE分析可知，在不同工況下，鋼板彈簧座附近受載情況最嚴重。選取該處整個截面作為優化變量。優化變量由寬度B，高度H和橋殼壁厚t這3個變量組成[9]。驅動橋最大應力至少為優化目標。

步驟2：構建響應面模型并驗證模型的準確性。驅動橋殼優化目標和設計變量確定后，運用拉丁方試驗設計方案，根據最小二乘法建立起橋殼目標函數的二次響應面近似模型。需對響應面模型進行精度驗證分析，因此須對其近似值做F檢驗[17]。若符合工程要求的置信水平，模型是有效的，可利用該近似模型進行優化；反之，需要重新構建新的響應面模型。

步驟3：設定設計變量初始值。利用驗證滿足精度要求后的近似模型代替實際有限元模型進行分析時，需設定設計變量初始值。

步驟4：利用響應面進行約束函數和函數可靠性分析。首先利用函數面法構建約束函數，然后對約束函數進行可靠性分析。

步驟 5：利用遺傳算法對步驟4的響應面模型進行分析，優化收斂則停止優化，獲得優化結果。

步驟6：若步驟5無法滿足最優解，則需要更新設計變量，回到步驟3，直到獲得滿意的優化結果。

基于響應面法橋殼可靠性優化流程見圖4。

圖4 基于響應面法的驅動橋殼可靠性優化流程Fig. 4 Reliability optimization process of drive axle housingbased on response surface method

4 實例分析

為減少試驗次數，提高計算效率，筆者采用拉丁方程設計了15次試驗，試驗實際值和響應值如表2。以3種工況下數值仿真試驗最大值作為原始數據點，由二次多項式構建的汽車橋殼響應面模型如式(5)：

(5)

式中：a1、a2、a3均為規范變量。

驅動橋殼結構優化前后結果如表3。由表3可知：優化后的橋殼最大應力降低了10.91%，橋殼質量降低了10.93%，橋殼可靠性提高了49%。對比文獻[9]，在保證可靠性同時采取響應面優化具有良好的優化效率和收斂性。由于工程需要，將截面寬度由162.31 mm調整為162 mm，將高度由163.45 mm調整為163 mm，橋殼壁厚由9.78 mm調整為10 mm。

將修改后的優化變量值代入響應面可靠性模型，并與有限元模型進行分析對比，如表4。從表4可知：基于響應面模型預測值與有限元模型計算值相對誤差在2%以內，優化結果具有較高的精度，基于響應面模型的優化結果滿足設計要求。

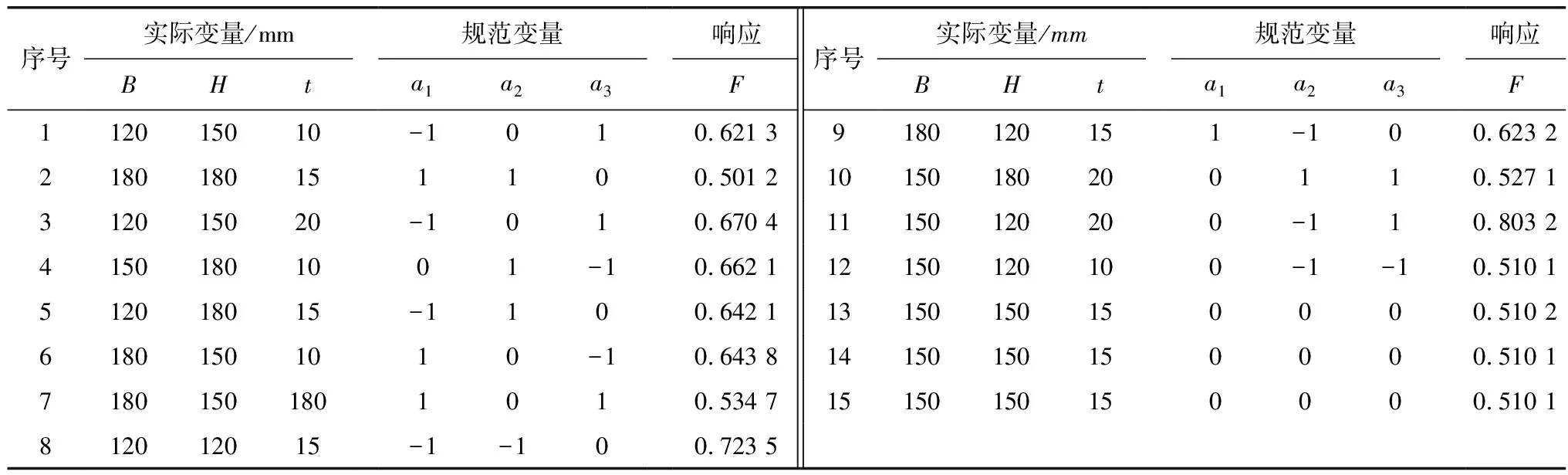
表2 實際值、編碼值和相應數據Table 2 Actual value, code value, and corresponding data

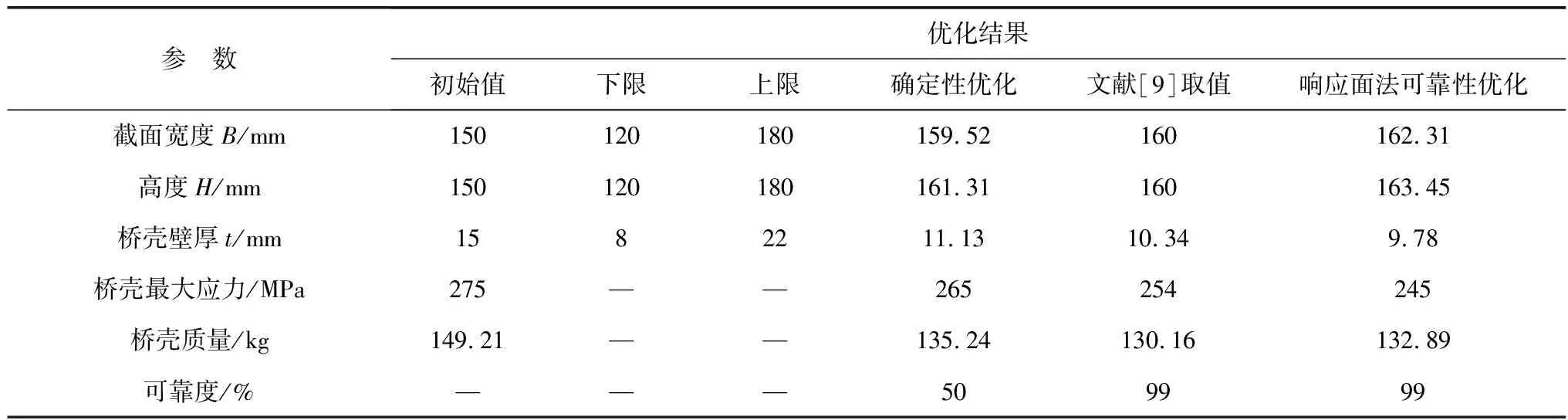
表3 驅動橋殼結構優化結果對比Table 3 Comparison of optimization results of drive axle housing structure

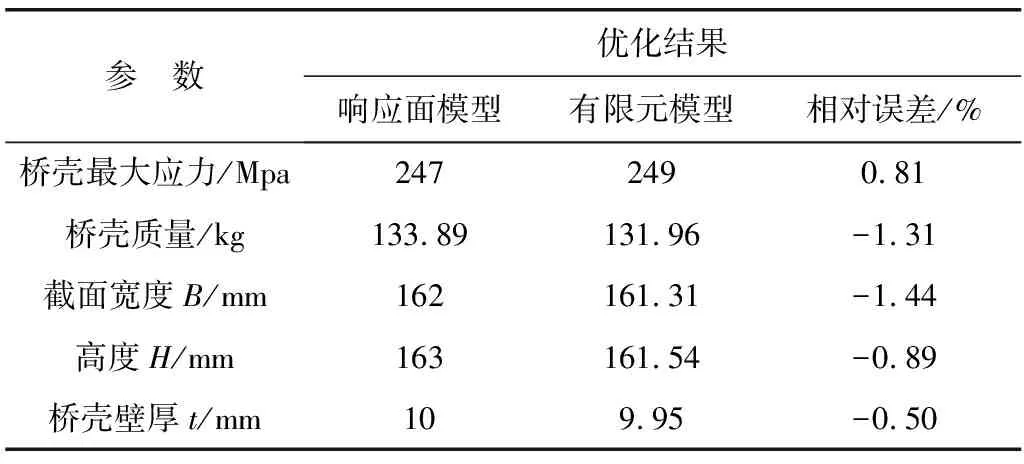
表4 優化結果精度對比Table 4 Precision comparison of optimization results

5 結 語

筆者將優化分析與可靠性技術相結合，基于響應面法對橋殼結構參數進行了可靠性優化。并以某驅動橋殼為例，建立了橋殼有限元模型，通過有限元分析得到優化目標區域，結合拉丁試驗設計構建了橋殼響應面近似模型。根據橋殼設計參數優化結果，優化后的橋殼最大應力降低了10.91%，橋殼質量降低了10.93%，滿足相應強度要求條件能有效降低橋殼質量。與直接有限元模型相比，應用響應面近似模型能快速準確地獲得最優值，且能有效解決工程優化時間長、效率低的問題，達到可靠性設計目的，為其他復雜結構優化設計提供借鑒。