改進指數平滑預測的虛擬機自適應遷移策略①

劉春霞,王 娜,黨偉超,白尚旺

(太原科技大學 計算機科學與技術學院,太原 030024)

近年來,隨著日益增長的計算、存儲和網絡需求,云計算數據中心能源消耗問題得到了越來越多的關注.據統計,2014年美國的數據中心消耗了700億千瓦時的電力,相當于該國全年能源消耗總量的1.8%.高能耗不僅造成高運營成本,而且會導致巨大的碳排放,每年信息和通信技術 (Information and Communication Technologies,ICT)產業對全球溫室氣體排放總量的貢獻率為2%左右[1].實際上,數據中心的能耗成本與服務器數目以及資源利用狀況密切相關,高能耗問題的主要原因是主機的資源利用率不均衡.因此,為了解決數據中心高能耗問題,研究人員利用虛擬機遷移技術實現數據中心各主機之間動態負載均衡,達到各主機的資源充分利用[2].虛擬機遷移技術即當數據中心物理主機的負載值不在合理范圍時,需要將分配在該主機上虛擬機遷移到合適的主機上,通過該方法能夠實現數據中心物理主機的動態負載均衡,使數據中心的資源可以合理利用,從而達到節能降耗的目的[3].但是,數據中心虛擬機遷移過程中,虛擬機遷移粒度較大,遷移時傳輸的數據量也大,因此,遷移開銷是不可忽略的.而數據中心負載量不斷動態變化的特殊環境會造成虛擬機因負載瞬時峰值而頻繁遷移,這將會產生一部分因虛擬機遷移而引發的能量損耗.因此,有必要對虛擬機遷移時機進行研究,避免物理主機瞬時過載而導致虛擬機頻繁遷移,以提高虛擬機遷移效率,在保證能耗降低的同時,盡量使得虛擬機的遷移次數達到最小.

當前,虛擬機遷移技術在云數據中心高能耗問題上的應用不斷改進與發展.文獻[4]采用基于閾值的方法來觸發虛擬機遷移,如果監測到物理主機的負載值高于閾值,則進行虛擬機遷移,否則,不需要虛擬機遷移.文獻[5]提出一種基于時間序列的預測方法,通過分析當前時間云資源負載值與下一時間預測值之間的變化關系,實現對云資源負載的動態調整,該方法通過資源調整來提高物理主機利用率.文獻[6]提出基于負載預測的動態虛擬機整合算法,通過預測物理主機的負載值來判斷物理主機是否處于過載或低載狀態,進而觸發虛擬機的遷移.文獻[7]在CloudSim工具中根據歷史數據,使用局部加權回歸 (the Local Regression,LR)法來預測未來時刻物理主機的資源負載狀態.文獻[8]通過布朗指數平滑法預測下一時刻物理主機的負載值,進而判斷物理主機的負載狀態,在一定程度上降低了數據中心能耗,但該方法所采用的平滑系數固定,難以適應數據中心負載不斷動態變化的情況,可能造成預測精度不高,導致虛擬機無效遷移.

綜上所述,關于云計算服務器虛擬機遷移策略的研究大多使用基于閾值或基于預測的方法,存在以下普遍缺陷:簡單基于閾值的方法不具有靈活性;簡單基于預測的方法需要時刻進行負載值的監測和預測,造成不必要的工作負載;由于數據中心瞬時的負載峰值,單一策略可能造成不必要的虛擬機遷移.文獻[8]采用的指數平滑預測方法是一種時間序列預測法,但其使用單一的平滑系數,難以適應數據中心這樣負載不斷變化的特殊環境.因此,本文提出一種基于改進指數平滑預測的虛擬機自適應遷移策略DyESP (Dynamic Exponential Smoothing Prediction),該策略將閾值和預測相結合,通過連續判斷物理主機負載狀態來觸發預測機制,使預測算法采用動態平滑系數,提高了預測精度,避免了因瞬時過載而導致的虛擬機無效遷移,從而提高了虛擬機遷移效率并降低能耗.

1 虛擬機自適應遷移策略

1.1 相關定義

虛擬機遷移過程一般分為三部分,即虛擬機何時遷移,選擇合適的虛擬機遷移以及選擇合適的目的主機完成遷移,其中虛擬機何時遷移是完成遷移過程的第一步也是最關鍵的一步,合理的虛擬機遷移觸發方法能提高虛擬機的遷移效率,降低數據中心的能耗.在對虛擬機遷移觸發方法進行描述之前,需要對虛擬機遷移過程的相關影響因素做如下定義:

定義1.將數據中心物理主機所構成的有限集合定義為H={h1,h2,h3,···,hn};將每臺物理主機hi上部署的虛擬機所構成的有限集合定義為Vi={vi1,vi2,vi3,···,vim}[9].

定義2.虛擬機遷移過程中,當物理主機符合遷出條件時,該物理主機稱作源主機,將所有源主機構成的有限集合定義為D;當物理主機符合遷入條件時,該物理主機稱作目的主機,將所有目的主機構成的有限集合定義為O;當物理主機既不符合遷出條件,也不符合遷入條件時,該物理主機稱為安全主機,將所有安全主機構成的有限集合定義為S,因此,H=DUOUS[9].

1.2 遷移策略

依據上述定義,本文提出基于指數平滑預測的自適應虛擬機遷移策略,該方法通過連續監測判斷和自適應預測兩部分來提高虛擬機遷移時機的準確性.由于物理主機的負載值過高或過低都會造成數據中心能量損耗,并影響服務質量,因此將監測值劃分為過載,低載和安全值三種狀態.過載表示為物理主機的負載值超過高閾值,此時需要依據歷史數據預測下一段時間的物理主機負載值;低載表示為物理主機的負載值低于低閾值,此時需要完成虛擬機的全部遷出并且關閉物理主機;安全值表示為物理主機的負載值處于高閾值和低閾值之間,此時不需要進行虛擬機遷移.本文選擇CPU利用率作為遷移觸發的主要影響因素,通過該方法能夠在一定程度上避免因瞬時峰值造成的虛擬機不必要遷移,提高虛擬機遷移效率.

(1)監測.為了使虛擬機遷移觸發方法更適應數據中心負載不斷變化的特殊環境,降低虛擬機無效遷移次數,本文通過連續監測4次物理主機的負載值來判斷其是否為待遷物理主機,若其連續監測值高于高閾值且呈上升趨勢,則將該物理主機看作待遷移物理主機.文獻[4]研究表明,當閾值過高時,由于數據中心物理主機持續高負載會產生大量能耗;當閾值過低時,會造成虛擬機的頻繁遷移,同樣會產生由于頻繁遷移而帶來的大量能耗,所以選取 0.8 為閾值.因此,本文同樣將0.8作為遷移觸發閾值.

(2)自適應預測機制.由于數據中心物理主機的負載值是動態變化的,連續監測物理主機的負載值超過閾值且呈上升趨勢,并不代表下一時刻其負載值一定超過閾值,因此,本文采用連續10次物理主機的歷史負載值,通過改進指數平滑預測法對待遷移物理主機的下一時刻負載值進行自適應預測.當預測值超過閾值時,將該物理主機看作需要進行遷移的物理主機,否則繼續進行監測.

該虛擬機遷移策略能判斷物理主機負載值的變化趨勢,并自適應的預測物理主機下一時刻負載值,提高了預測精度,有效的避免了因主機負載的瞬時過載而導致虛擬機無效遷移,從而提高了虛擬機遷移的準確性,減少了虛擬機無效遷移次數,進而降低了數據中心能耗.該方法的流程圖如圖1所示.

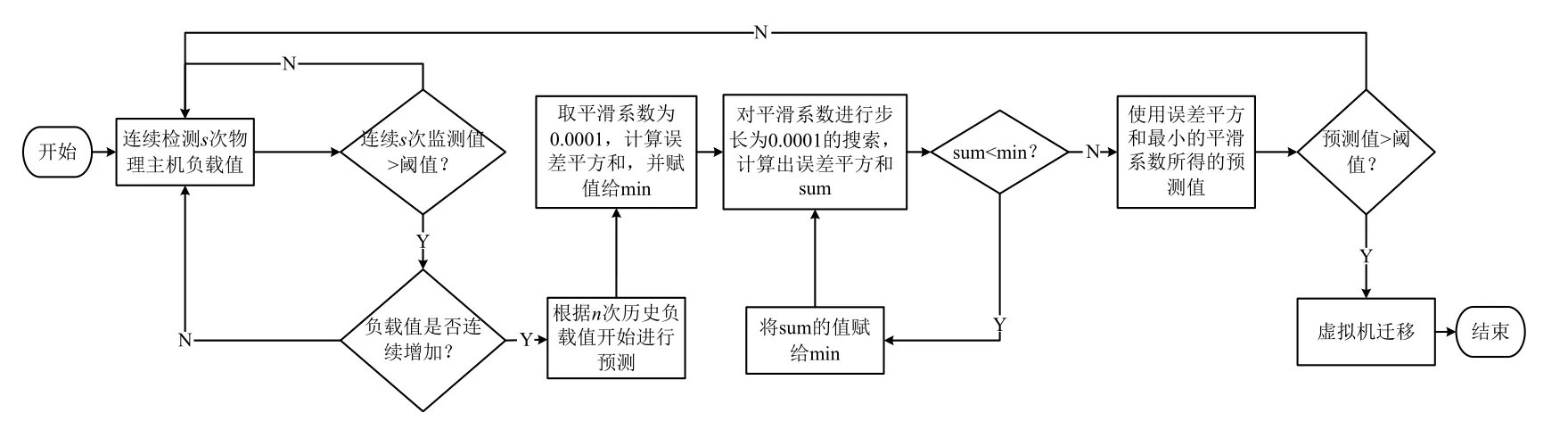
圖1 觸發預測流程圖

2 自適應預測機制

2.1 指數平滑預測法

二指數平滑法 ESP(Exponential Smoothing Prediction)是基于移動加權平均法來預測時間序列變化趨勢的方法,該方法為最近的觀測數據賦予較大的權值,給距離較遠的觀測值賦予較小的權值,以此預測下一時刻的值,適用于中短期趨勢預測[10].設遷移觸發過程中需要s個時間段,其序列定義為 〈t1,t2,t3,···,ts〉,其中每個時間段的物理主機負載檢測值定義為 〈y1,y2,y3,···,ys〉,因此,遷移觸發過程中的數據集合定義為:

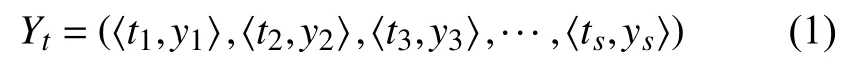
一次指數平滑法的定義為:

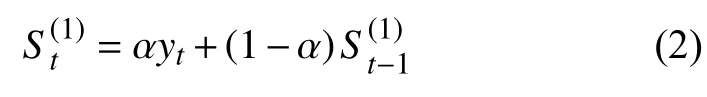
一次指數平滑法雖然可以較好的預測趨勢變化明顯的情況,但具有較大的滯后性,因此,本文采用二次指數平滑預測法,其定義為:

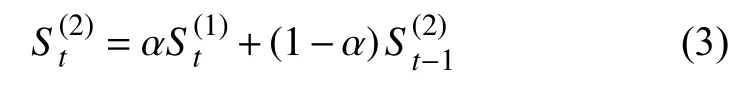
二次指數平滑預測法需建立線性趨勢預測模型,其模型為:

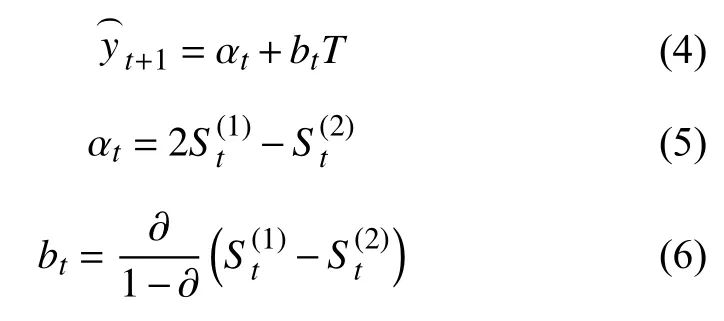
其中,t表示當前時間;T表示當前時間t到未來時間t+T之間的時間段;表示第t+T時間段的預測值;αt為截距;bt為斜率.

在實際的操作中,需要連續檢測s次負載值,如果都超過閾值,并且負載值呈現上升趨勢,則進行預測,利用二次指數平滑預測法計算出截距αt和斜率bt,并利用式(7)進行預測,得到時間T的負載值.

二次指數平滑法能較好的預測負載的變化趨勢,對數據中心負載值的變化做出合理的判斷,如果預測值在合理的負載范圍內,則不需要進行虛擬機遷移,否則,需要進行虛擬機遷移.

2.2 自適應預測機制

指數平滑法預測的過程中,平滑系數表示數據的變化趨勢.ESP方法中,平滑系數一經確定便是一個常數,難以跟蹤數據變化,導致降低了預測過程的適應性.針對云數據中心負載不斷動態變化的特點,如果僅采用一個平滑系數,難以適應整體的變化過程,所以本文采用動態平滑系數對傳統模型進行修正[11].

采用動態平滑系數是指在預測的過程中能夠使平滑系數自適應數據中心的特殊環境,隨實際數據的變化而變化.在傳統指數平滑預測模型中,平滑系數的選擇決定了預測精度的高低,當檢測的數據呈水平趨勢時,平滑系數應該選取0.1-0.3,當檢測的數據呈持續上升或下降趨勢時,平滑系數則應該選取0.3-0.5,當波動較大時,應選取 0.6-0.8[8],因此,當數據的變化趨勢發生改變時,單一的平滑系數很難適應預測需求.為了使預測方法能夠更好的適應數據中心不斷動態變化的特殊情況,本文的自適應預測機制采用動態平滑系數,即在負載值預測的過程中,平滑系數隨著數據的變化而自動調整,能夠很好的適應數據變化的真實情況,得到更精確的的預測結果.自適應預測機制的具體過程為:

(1)確定實際數據.將連續檢測到的T期物理主機歷史負載值作為預測機制的初始數據.本文中使用10期歷史數據作為實際數據.

(2)查找最優的平滑系數.通過迭代法查找最優的平滑系數,選取步長為0.0001對平滑系數進行迭代,而后利用二次指數平滑預測法求出T期數據的誤差平方和,依據誤差平方和最小原則獲得最優的平滑系數σ,即:

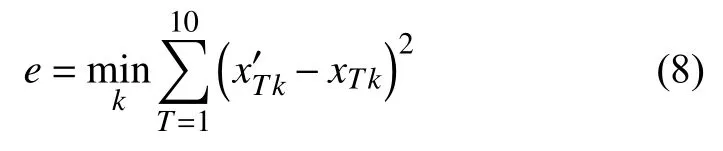
式中,k表示平滑系數,取值在0～1范圍內以步長0.0001 迭代;表示當平滑系數為k時第T期數據的預測值;xTk表示平滑系數為k時第T期數據的實際值;求出不同平滑系數對應的T期數據的誤差平方和,并利用最小原則求出最小的誤差平方和,最小誤差平方和對應的平滑系數即為最優的平滑系數.

(3)預測第T+1期的負載值.將步驟(2)獲得的最優平滑系數帶入二次指數平滑預測法中進行預測,獲得T+1期的物理主機負載值.

(4)遷移觸發.將步驟(3)獲得的預測值與閾值進行比較,當預測值大于閾值時,說明該物理主機呈現持續過載狀態,需要將該物理主機上合適的虛擬機遷移到適當的目的主機上,使數據中心的各物理主機達到負載均衡;當預測值小于閾值時,說明該物理主機只是處于短暫過載狀態,下一時刻已經不再處于過載狀態,因此,不需要進行虛擬機遷移.

傳統二次指數平滑預測方法中初始值的選擇,當數據量較小時,選取第一期的實際值作為初始值,當數據量較大時,選取前三期的平均值作為初始值.本文將第一個時間段的實際值做為初始值進行預測.

3 實驗與結果分析

CloudSim云計算仿真平臺[12]是一個可擴展的仿真工具包,它支持云計算系統和應用程序供應環境的建模和模擬.為了驗證本文提出的動態指數平滑預測方法的有效性,利用CloudSim3.0版本對該方法進行仿真實驗,并與LR和ESP兩種預測方法進行實驗對比分析.其中,局部線性回歸法是對物理節點的歷史數據進行線性擬合,從而得到擬合曲線函數,進而預測得出物理節點下一時間段的負載值.本文采用的評價指標是數據中心能耗值和虛擬機遷移次數.

通過CloudSim模擬了云數據中心,其中包括800臺物理主機,1052個虛擬機.物理主機由如表1兩種型號組成.為了使該實驗具有現實意義,采用來自COMON項目中監測PlanetLab平臺在2011年3月3日這一天的CPU利用率數據作為數據中心物理主機實際負載值,該數據每5 min采集一次,在24 h內共采集了288個樣本點.

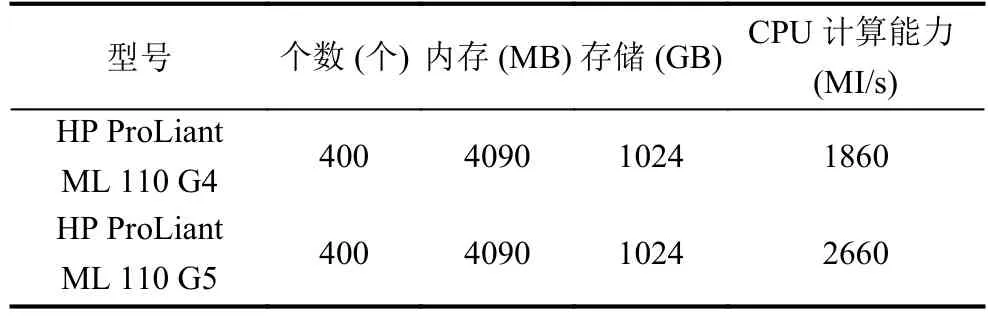
表1 物理主機組成

在進行對比實驗之前,為了找出傳統二次指數平滑預測方法中預測精度最高的平滑系數,本文從采集到的物理主機實際負載值中選取連續10期負載值作為實際值,分別使用平滑系數值為0.4、0.5、0.6、0.7和0.8進行預測分析,并計算得到相應的標準方差值,如圖2所示,可以看出,當平滑系數的取值是0.6時,所獲得的標準方差值較小,即預測精度較高.因此,采用平滑系數為0.6的ESP方法與本文的DyESP方法進行實驗對比分析.

如圖3所示,展現了當實際數據取不同期數時,使用平滑系數為0.6的ESP方法得到的各期誤差和與使用本文的自適應預測機制得到的各期誤差和的對比結果.由圖可知,使用自適應預測機制所得出的誤差和比使用ESP方法所得出的誤差和小,說明使用自適應預測機制精度更高.由圖得知,當期數大于 10 期時,誤差和趨于穩定,說明各期數據的誤差相對于低于10期時更小,精度更高.因此,本文采用 10 期的歷史負載值作為預測的實際值.

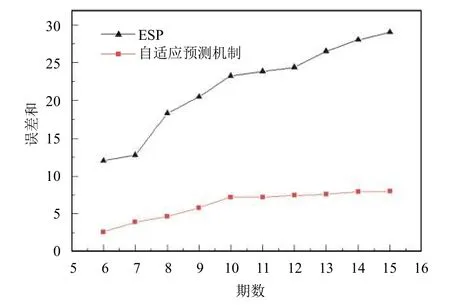
圖3 不用期數的誤差和對比

如圖4所示,展現了使用平滑系數為0.6的ESP方法得到的下一時刻預測值與實際值的誤差以及使用本文的自適應預測機制得到下一時刻負載值與預測值的誤差對比.該實驗采用連續10期物理主機歷史負載值作為初始數據,分別使用ESP方法和DyESP方法對其進行預測,將預測值與實際第11期數據進行比較,獲得誤差值.圖4由圖可知,使用自適應預測機制得到的誤差比使用二次指數平滑預測法得到的誤差小,即預測的精度相對較高.

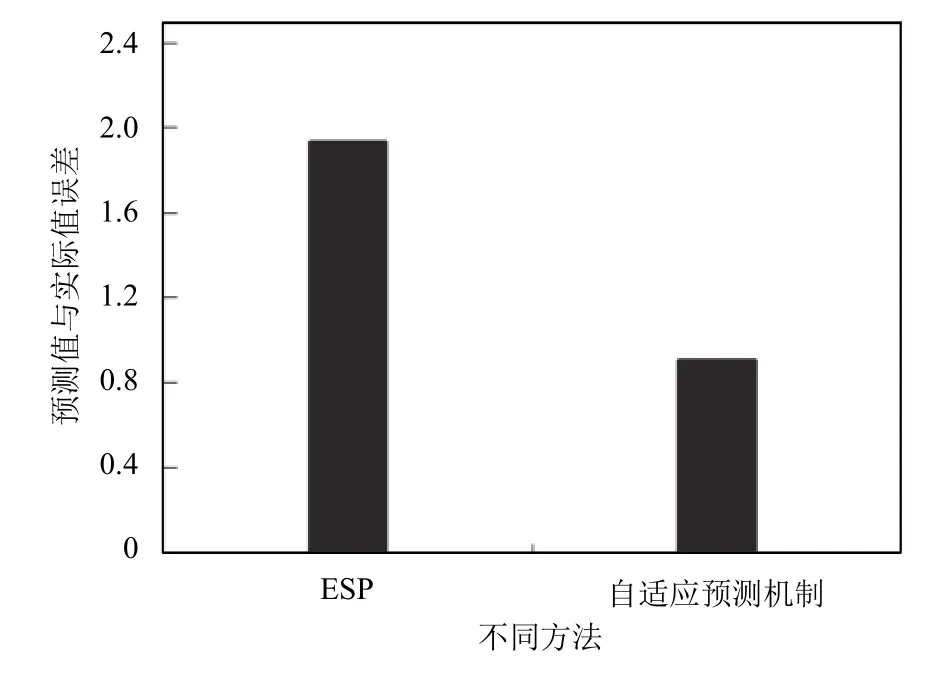
圖4 不同方法預測值與實際值誤差

如表2所示,是分別使用LR方法、ESP方法和本文提出的DyESP方法獲得的數據中心能耗值以及虛擬機遷移次數的實驗結果對比.結果表明,與LR和ESP相比,本文的DyESP方法在數據中心能耗方面分別降低約為34.26%、7.34%;虛擬機遷移次數方面分別降低約為80.99%、58.55%.

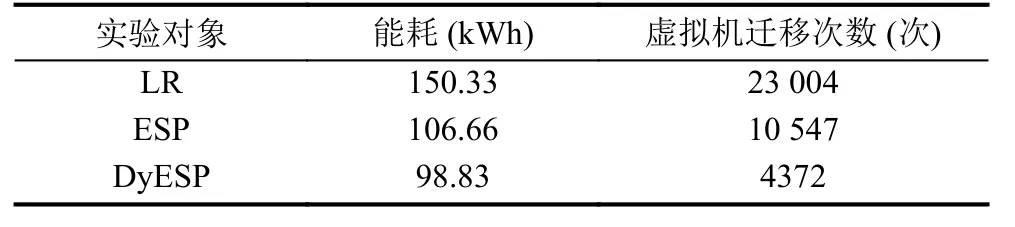
表2 實驗結果

圖5是數據中心能耗值隨時間變化的趨勢.該對比實驗分別對一天內第 4 h、8 h、12 h、16 h 和 20 h的能耗值進行數據檢測記錄,從圖中能夠看出,相比LR和ESP方法,本文提出的DyESP方法在4 h和8 h時監測到的數據中心能耗沒有明顯的降低,因為,此刻數據中心物理主機剛開始工作,處理任務時間較短,任務量較少,所產生的能耗沒有較大差距,但隨著時間的延長,物理主機處理的任務越來越多,各個物理主機的資源利用率越來越大,數據中心所產生的能耗量也越來越大,此時,采用不同預測算法所獲得的能耗值差距也在不斷增大,由圖3可以看出,本文的DyESP方法在降低能耗方面有較明顯的優勢.

圖6是虛擬機的遷移次數隨時間變化的趨勢.該對比實驗同樣對一天內第 4 h、8 h、12 h、16 h 和 20 h的能耗值進行數據檢測記錄,相比LR和ESP方法,本文提出的DyESP方法在4 h時檢測到虛擬機遷移次數下降趨勢不明顯,主要原因是數據中心物理主機一開始處理的任務量較少,資源占用率低,物理主機出現過載狀態較少,因此,需要進行虛擬機遷移的情況較少.但隨著時間推移,數據中心中各物理主機需要處理的任務量逐漸增加,物理主機的資源利用率開始不斷增加,使得物理主機出現過載狀態的情況越來越多因此,虛擬機遷移次數開始不斷增加,由圖6可以看出,采用不同預測算法所得到的虛擬機遷移次數的差距在不斷增大,由圖可知,本文的DyESP方法在降低虛擬機遷移次數方面有明顯的優勢.

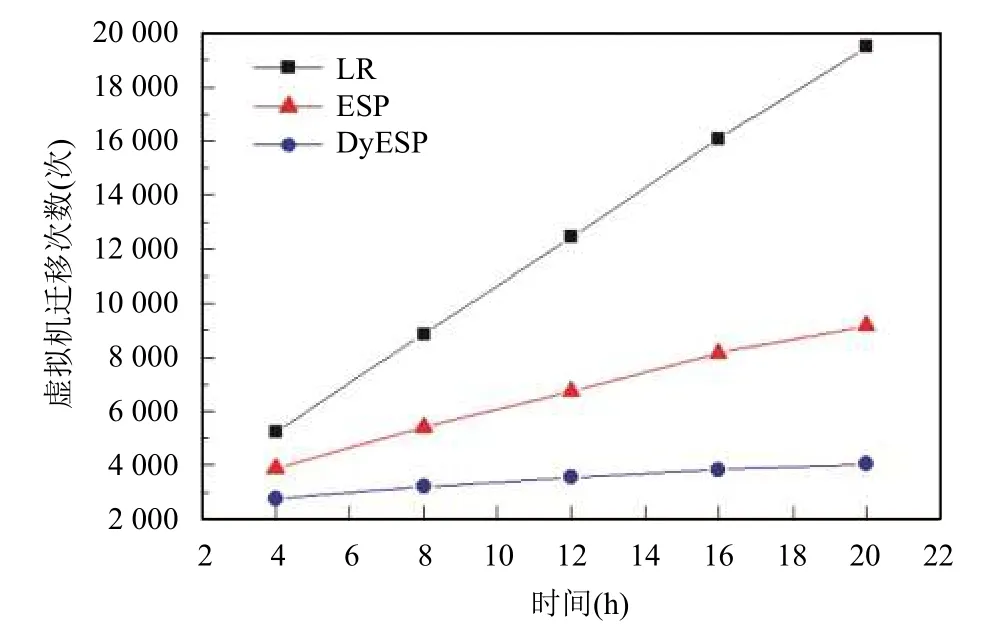
圖6 虛擬機遷移次數隨時間變化

圖7是數據中心在2011年3月3日這一天的平均違例率.違例率的大小展示了數據中心服務質量的好壞,違例率越小,說明服務質量越好;反之,服務質量越差.由圖可知,DyESP方法相較于LR方法違例率有所提高,而與 ESP 方法相比,違例率有所下降.說明,本文提出的自適應策略所提供的服務質量比ESP方法高,但沒有LR方法提供的服務質量高.結合圖5和圖6的結果可知,本文提出的方法在降低能耗和降低虛擬機遷移次數方面都有較明顯的優勢,而在服務質量方面的優勢不足,這需要進一步的研究.

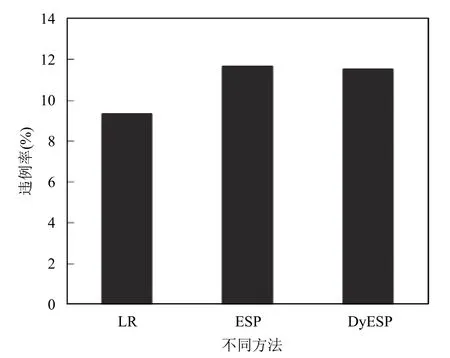
圖7 不同方法違例率對比

4 結論

本文提出一種基于指數平滑預測的虛擬機自適應遷移策略,通過判斷s期主機負載值是否連續超過閾值并呈上升趨勢來觸發預測,然后根據連續n期歷史數據自適應選擇平滑系數預測下一時刻的負載值,從而觸發虛擬機遷移,該方法將雙閾值和預測相結合,在一定程度上提高了預測精度,避免了因瞬時峰值而導致的虛擬機無效遷移.經實驗表明,本文提出的DyESP方法在提高預測精度、降低虛擬機遷移次數以及降低數據中心能耗方面有較明顯的優勢.下一步的工作是將本文提出的自適應遷移策略進一步改進,使其在滿足數據中心能耗和虛擬機遷移次數都降低的同時,保證數據中心的服務質量.