考慮點腐蝕影響的船體板疲勞壽命評估

陳憲剛

(海軍裝備部駐上海地區軍事代表局駐上海地區第五軍事代表室，上海 201913)

0 引言

在船體結構設計中，疲勞性能是不可忽略的一個方面。由于船體長期服役在交變波浪載荷中，所以對于船體結構，疲勞是構件的主要失效形式。統計結果表明，在各種機械的斷裂事故中，有80%以上是由于疲勞失效引起的[1]。因此，對于承受交變應力的構件，疲勞分析在設計建造和維修決策中占有重要的地位。

長期服役在海水中的船體構件，不可避免地會受到海水腐蝕作用，產生均勻腐蝕和點腐蝕[2]。學者們大量研究了腐蝕損傷對船體結構極限強度的影響。張巖等[3]指出在點蝕加筋板的有限元建模中蝕坑可以假設成圓柱形，而加筋板自身可以離散成殼單元，但不同于屈曲分析的是，應力集中分析對蝕坑形狀和蝕坑深度極為敏感，可見，應用體單元進行不同形狀的蝕坑建模在疲勞分析中是極為必要的。SULTANA等[4]基于有限元分析研究了隨機腐蝕對海洋結構單元壓縮強度的影響，結果發現相對于加筋板，非加筋板由于腐蝕引起的體積損失對極限強度的降低比加筋板更多，達到45%。TEIXEIRA等[5]提出了一種對具有隨機性結構系統的響應評估方法，并將由半經驗設計方程或非線性有限元分析(FEA)的隨機初始扭曲作用下計及材料非線性和幾何非線性的銹蝕鋼板極限強度分析作為一個案例來證明所提出方法的準確性。

雖然目前國內外對腐蝕造成的船體板結構剩余強度研究日趨成熟，但由于腐蝕的存在對疲勞強度降低的影響卻鮮有研究。即使中國船級社(CCS)最新的《船體結構疲勞強度指南》[6]對設計應力范圍的計算計及了均勻腐蝕修正系數，但其并未考慮點腐蝕的影響。由于蝕坑處在軸向載荷的作用下會產生應力集中，所以疲勞問題在蝕坑處更為敏感。開展船體全壽命周期內的船體結構可靠性分析必須考慮腐蝕和疲勞等損傷形式對結構抗力的影響，否則可靠性評估結果不能表征船體結構的真實狀態[7]。本文將基于蝕坑處的應力集中系數，分析考慮點腐蝕影響的船體板疲勞壽命評估方法。

1 點腐蝕應力集中系數

對于點腐蝕，不同的蝕坑形狀其應力集中系數不盡相同。文獻[8]指出，點腐蝕蝕坑形狀主要有圓柱形、半圓形和圓錐形3種。對于圓柱形蝕坑，文獻[9]指出孔邊應力集中系數最為敏感。應力集中系數kS隨蝕坑深度的變化關系可按下式計算：

kS=3+0.55ln(h/t)

(1)

式中：t為板厚；h為蝕坑深度。

本文將重點對半圓形和圓錐形蝕坑應力集中系數進行計算。

1.1 半圓形蝕坑

本文設方板的邊長為a，板厚為t，蝕坑的直徑為0.1a，深度為h(h=0.2t、0.4t、0.6t、0.8t、t)。材料的密度為7 850 kg/m3，泊松比為0.3，楊氏模量為2.1×105MPa。本文使用C3D8R單元(8節點線性六面體縮減積分沙漏控制單元)，劃分網格5 946個，在模型上施加235 MPa的單軸拉伸載荷，見圖1。

經計算，5種情況下的應力云圖見圖2，應力集中系數隨蝕坑深度的變化關系見圖3。從圖中可以看出，應力集中系數隨蝕坑深度的增加而增大，兩者基本上呈線性關系。

圖1 半圓形蝕坑網格的劃分及載荷的施加

圖2 半圓形蝕坑應力云圖

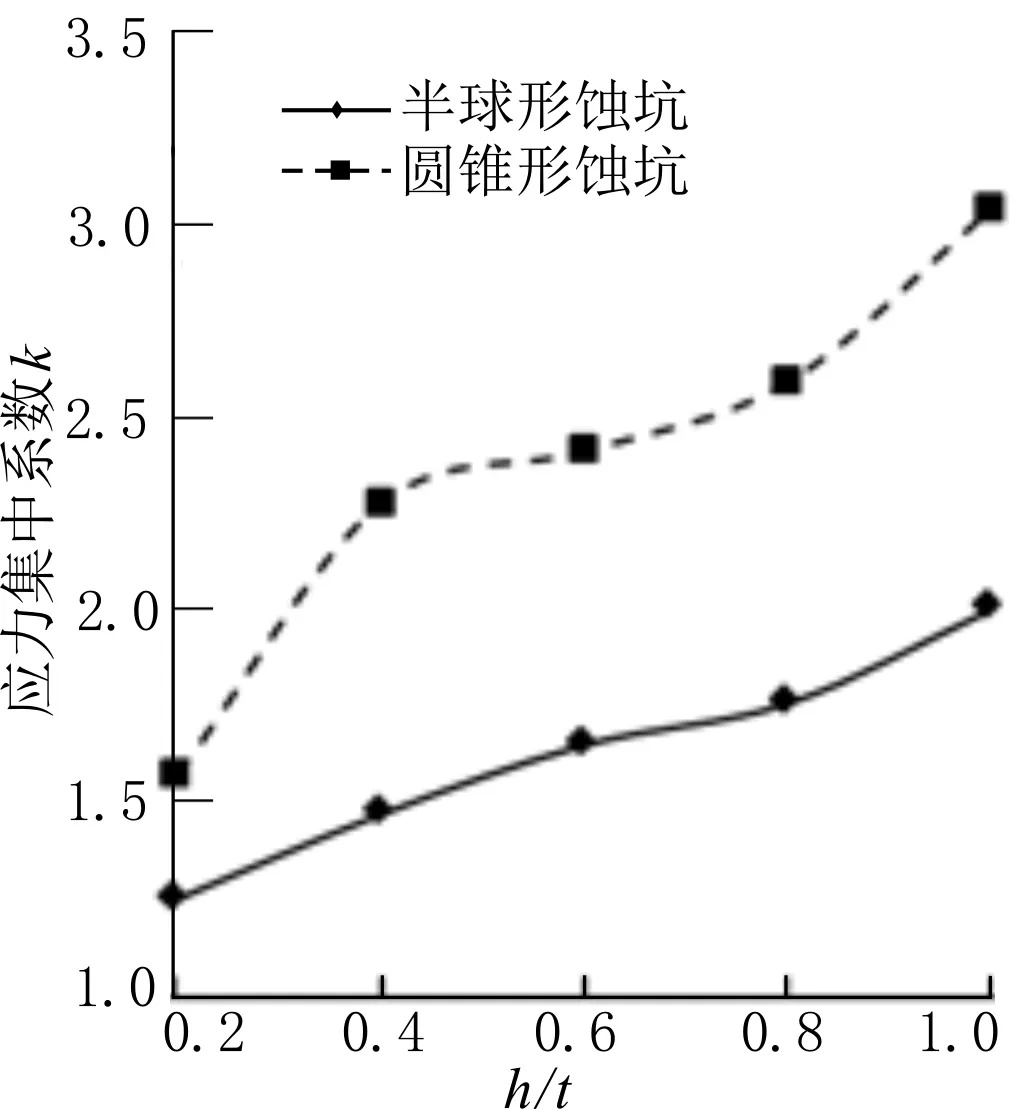
圖3 應力集中系數隨蝕坑深度的變化

1.2 圓錐形蝕坑

本文設方板的邊長為a，板厚為t，蝕坑的直徑為0.1a，深度為h(h=0.2t、0.4t、0.6t、0.8t、t)。密度為7 850 kg/m3，泊松比0.3，楊氏模量為2.1×105MPa。使用C3D10單元(10節點二次四面體單元)，劃分網格7 363個。在模型上施加235 MPa的單軸拉伸載荷，見圖4。

經計算，5種情況下的應力云圖見圖5，應力集中系數隨蝕坑深度的變化關系見圖3。從圖中可以看出，應力集中系數隨蝕坑深度的增加而增大，兩者呈線性關系；相對于半球形蝕坑，圓錐形蝕坑在單軸拉伸載荷下的應力集中系數不僅更大，而且對蝕坑深度也更為敏感。

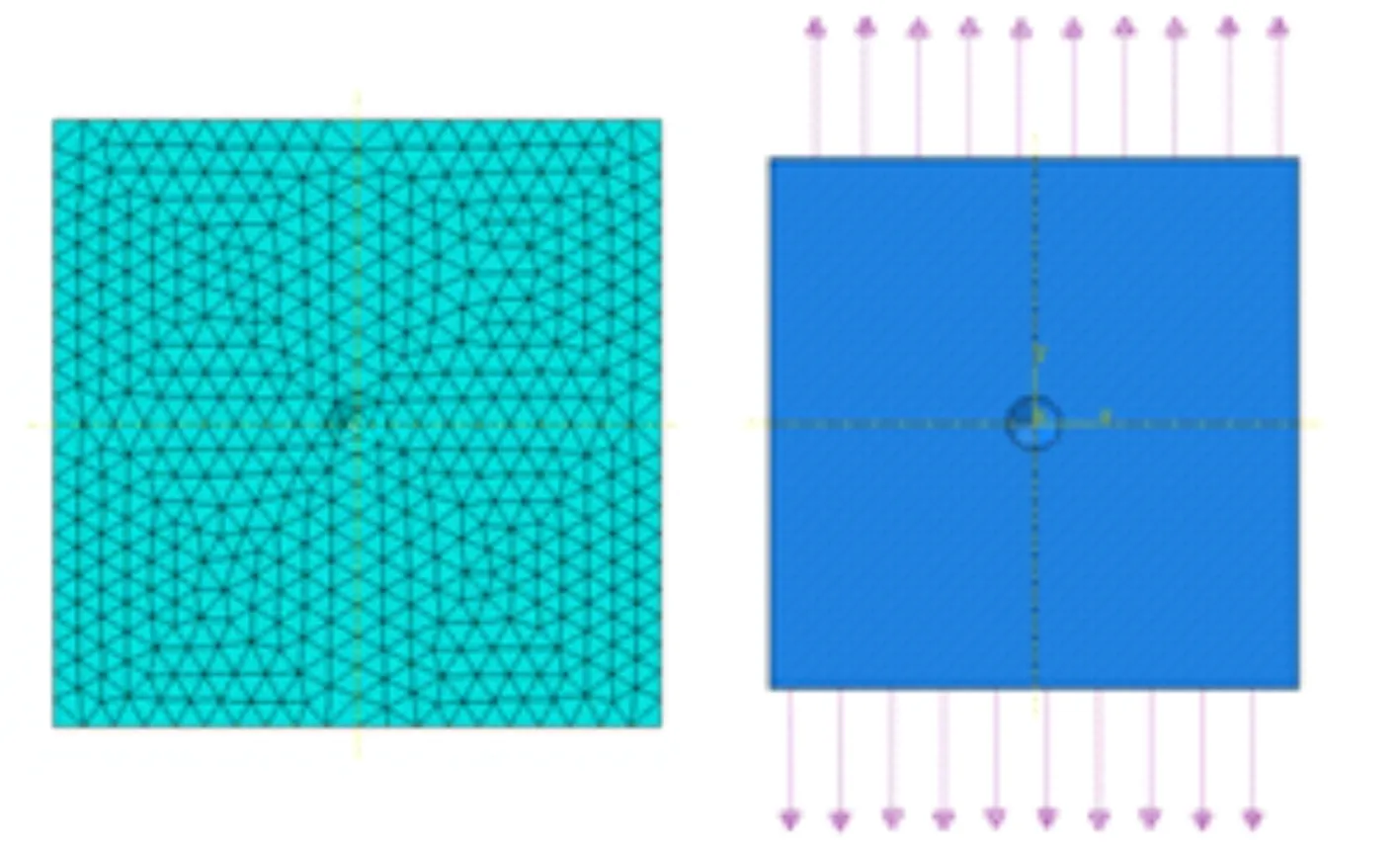
圖4 圓錐形蝕坑網格的劃分及載荷的施加

圖5 圓錐形蝕坑應力云圖

2 設計應力范圍計算

設計應力范圍按下式計算[10]：

SDk=kS|σhog,k-σsag,k|fkfcft

(2)

式中：SDk為第k工況(正常排水量、標準排水量、滿載排水量)的設計應力范圍；kS為典型節點應力集中系數，由式(1)計算得到；σhog,k和σsag,k分別為第k工況下中拱和中垂狀態下的名義應力，由粗網格模型有限元計算得到，本文采用文獻[11]中的算例(圖 6)，σhog,k和σsag,k分別取49 MPa和-51 MPa；fk為第k個工況的平均應力修正系數，按《船體結構疲勞強度指南》中的相關規定計算，由于本文的算例既非焊接節點，也非母材自由邊，所以fk取1；fc為腐蝕修正系數，對于簡化應力分析時船體梁彎曲正應力和有限元應力分析時總體載荷工況下的熱點應力，腐蝕修正系數fc=1.05；ft為板厚修正系數，當t≤22時，ft=1.0。

圖6 文獻[11]中的算例

3 累積損傷度的計算

目標船壽命期內累積損傷度Dk計算基于S-N曲線和Weibull分布模型，按下式計算：

(3)

D=∑Dk

(4)

μk=

(5)

vk=(Sq/SDk)ξklnNL

(6)

(7)

(8)

式(3)～式(8)中：ND為船舶在20 a營運期間的載荷循環總次數，通常取6.5×107。NL為載荷譜回復周期的循環次數，取102。αk為裝載工況“(k)”的時間分配系數，本文只考慮一種裝載工況，αk取1。K為S-N曲線參數，見表 1。D為結構節點的總累積損傷度，參考新版本《船體結構疲勞強度指南》對于S-N曲線選取的建議，對于焊接節點，疲勞強度評估采用D曲線；對于母材自由邊，疲勞強度評估采用C曲線。ξk為裝載工況“(k)”的Weibull形狀參數，取為1。m為S-N曲線反斜率，取為3。m為S-N曲線兩段反斜率差，取為2。γ(x,vk)為不完全GAMMA函數值。T為完全GAMMA函數值。Sq為S-N曲線二線段的交點處的應力幅值，見表 1。

表1 S-N曲線參數表

以上計算基于船舶的20 a營運期，得到結構在壽命期內的累積損傷度，結構的疲勞壽命TF即可按下式計算：

TF=20/D

(9)

對于半球形、圓柱形和圓錐形三種蝕坑，其疲勞壽命隨蝕坑深度的變化見表2和圖7。

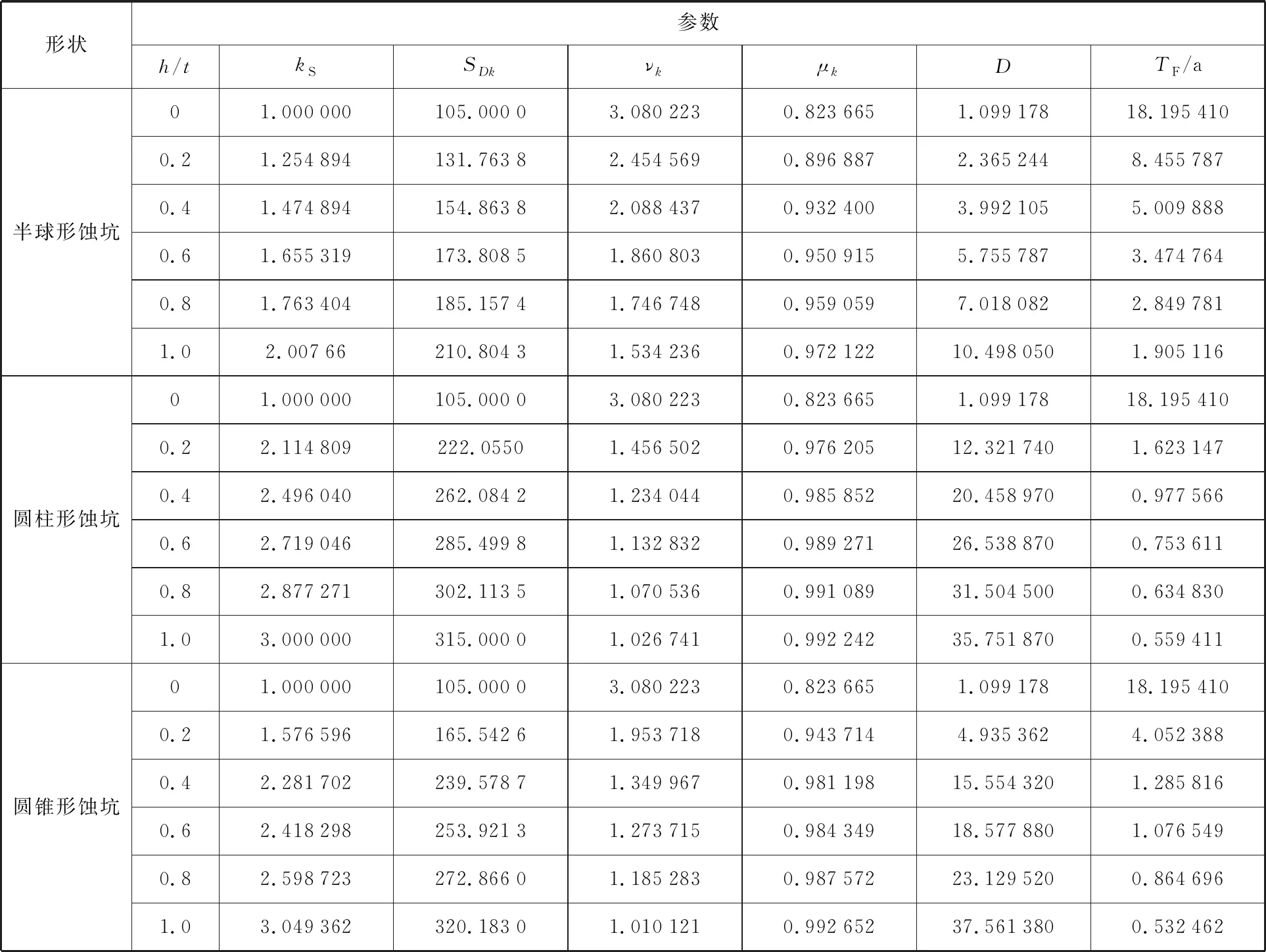
表2 3種蝕坑疲勞壽命隨蝕坑深度的變化

注：h/t為蝕坑深度/板厚；kS為應力集中系數；SDk為設計應力范圍；νk為系數，由式(6)給出；μk為系數，由式(5)給出；D為結構節點的總累積損傷度；TF為結構的疲勞壽命。

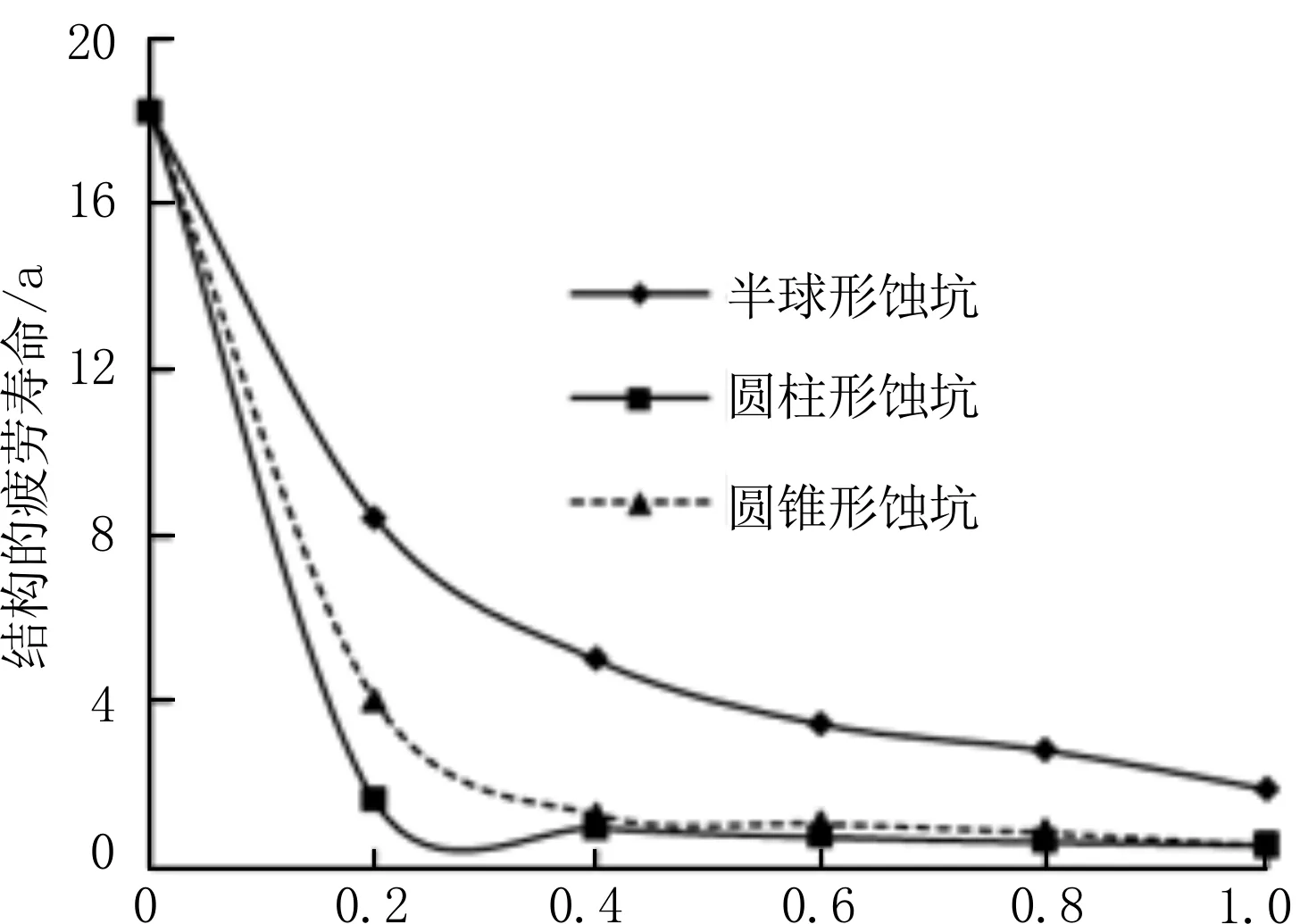
圖7 3種蝕坑疲勞壽命隨蝕坑深度的變化

由表 2和圖 7可知，當蝕坑深度為0，即無點腐蝕時，累積損傷度約為1，結構的疲勞壽命約等于設計壽命，這與客觀事實是相符的，驗證了基于應力集中系數計算結構疲勞壽命的合理性。由表 2可知，當蝕坑深度僅為0.2倍板厚時，含3種蝕坑的板單元疲勞壽命迅速由18.2 a減小到8.5、1.6、4.1 a，說明結構的疲勞壽命對點腐蝕極為敏感。對于3種蝕坑，其敏感順序為：圓柱形蝕坑>圓錐形蝕坑>半球形蝕坑。圖7更加直觀地展示出結構的疲勞壽命隨蝕坑深度的增大急劇減小，當蝕坑深度達到板厚時，板單元被蝕穿，此時結構幾近失效。

4 結論

本文基于點腐蝕蝕坑處的應力集中系數計算了含點腐蝕板單元的疲勞壽命，根據本文的計算可得到如下結論或發現：

(1)對于半球形蝕坑，蝕坑處應力集中系數隨蝕坑深度的增加而增大，兩者基本上呈線性關系。

(2)當蝕坑深度為0，即無點腐蝕時，累積損傷度約為1，結構的疲勞壽命約等于設計壽命。這與客觀事實是相符的，驗證了基于應力集中系數計算結構疲勞壽命的合理性。

(3)當蝕坑深度僅為0.2倍板厚時，含3種蝕坑的板單元疲勞壽命迅速由18.2 a減小到8.5、1.6、4.1 a，說明結構疲勞壽命對點腐蝕極為敏感。

(4)結構的疲勞壽命隨蝕坑深度的增大急劇減小；當蝕坑深度達到板厚時，板單元被蝕穿。

(5)如果產生點腐蝕，則會產生很多點腐蝕坑。本文只是考慮一個點腐蝕，多個點腐蝕共同作用是下一步研究方向。