基于空間插值的室內濕度場模擬方法比較分析

鄭世健，付 聰,2，萬博雨，劉知貴

(1.西南科技大學信息工程學院，四川 綿陽 621000；2.中國工程物理研究院電子工程研究所，四川 綿陽 621000)

在室內環境中，空氣速度、溫濕度等參數的優化對室內事物或人具有重要意義[1]。例如：在圖書館[2]，良好的室內環境可以保證讀者的健康和舒適性；在溫室[3]，良好的室內環境可以促進作物的生長和成活率。為了評估這些參數的詳細分布，一般采用兩種主要方法：計算流體力學(CFD)數值模擬和現場測量。CFD模擬方法的精確度極大的依賴于建模的精細程度和迭代計算模型的準確程度，與現實的環境存在明顯差異。雖然現場測量耗時和耗財，但數據更可靠。此外，即使在數值模擬中，也常需要一定數量的實驗數據來驗證計算結果，因此，現場測量是一種最好的方式。

目前，室內空氣參數分布的現場測量方式主要有利用光學和點式測量。光學測量方法采用粒子條紋測速、粒子跟蹤測速等光學測速技術，以獲取和處理被測粒子的反射信號來測量空氣分布，該方法可以確定局部場中的空氣速度分布。然而受環境空間中物體的影響較大。采用點式傳感器測量空氣參數，如熱電偶、風速計和氣體采樣器等。與光學方法相比，由于傳感器可以靈活的部署在測量的空間中，點式測量方法更適用于復雜的空間。這種測量方式只能測量單點的空氣參數，而空間中空氣參數是一個變化的域場，僅僅使用一個單點數據來反映整體情況，容易造成區域災難。為了描述整體空間變化情況，學者使用空間插值的方法進行模擬，以獲取整個區域內環境因子的總體分布情況。空間插值方法[4]主要包括地理統計方法和確定性方法。不同的研究尺度、環境要素和目的決定了使用不同的插值方法會產生不同的效果。董志南等人[5]在風場的插值研究中針對反距離權重插值、全局多項式插值、局域多項式插值、最近鄰域法插值、徑向基函數插值、普通克里金插值6 種空間插值方法進行比較，表明反距離權重插值在風場研究重要優于其他幾種方法；丁卉等人[6]基于環境監測站的空氣污染物濃度數據，采用反距離加權、規則樣條函數和克里金插值函數分別分析了不同空氣污染物、不同季節的空間插值效果，表明克里金法能夠得到最優的插值精度，但空間分布上過渡平滑性欠佳；楊順華等人[7]利用地理加權回歸克里金和回歸克里金對土壤有機質進行對比分析，得出地理加權回歸克里金方法對于土壤有機質的局部模擬效果優于回歸克里金的方法。

以上研究針對不同環境要素、不同研究尺度等情況，適宜的插值方法也不盡相同。調研發現：空間插值方法在降雨量時空分布、土壤和地區氣候時空變化方面應用較為廣泛，在室內有限空間區域濕度場研究較少，且大部分都是選中特定某種插值方法進行應用，而系統的比較不同插值方法效果的研究較少。本文以英特爾伯克利實驗區域為例，對室內濕度監測數據進行研究分析，觀測數據分布特征；利用6種空間插值方法對其進行空間插值估算；且使用交叉驗證法和其他一些參數對插值結果分析。

1 濕度場模擬研究區域概況與數據源

英特爾伯克利實驗室整體面積約為1 260 m2，具體的空間布局和傳感器分布圖如圖1所示。使用的環境傳感器為帶有防風雨板的Miaca2Dot傳感器(溫度、濕度、光照、電壓)，通過在TinyOS平臺構建的TinyDB網絡處理系統進行收集和處理。最終得到室內54個環境傳感器的濕度數據進行研究。

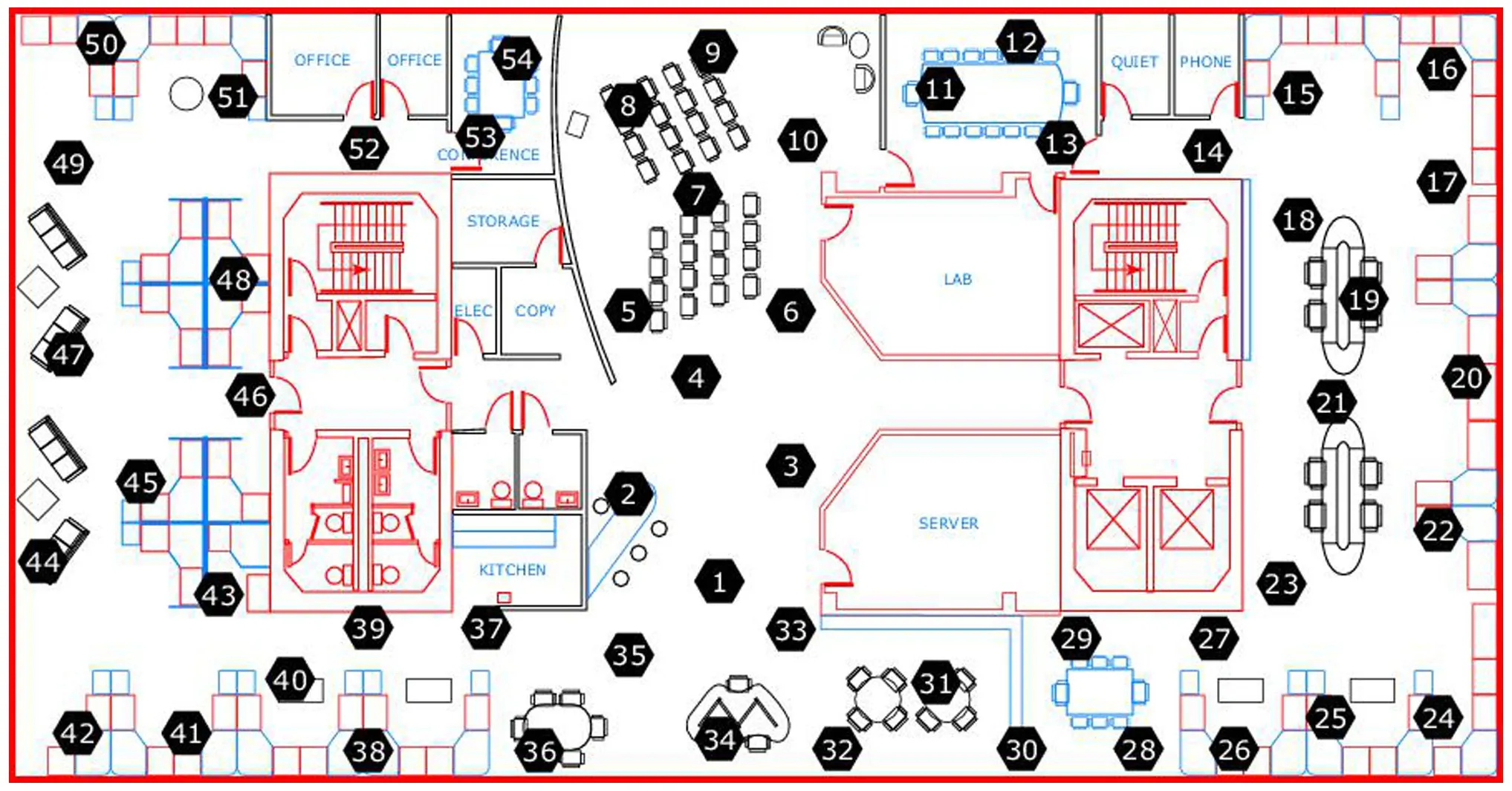
圖1 實驗室傳感器分布圖Fig.1 Laboratory sensor distribution map

試驗基礎數據來源于英特爾伯克利研究實驗室2004年2月28日至4月5日部署的54個傳感器采集的公共數據集。本文提取2004年3月份的檢測數據作為試驗基礎數據，所獲取的數據信息主要包括54個傳感器的地理位置信息及空氣溫濕度數據。地理位置信息主要是以實驗室右上角為原點建立的直角坐標系來描述的。

2 研究與評價方法

2.1 空間插值方法

(1)反距離權重插值。反距離權重插值法[8](Inverse Distance Weighting，IDW)是通過計算未測量點附近點測量值的加權平均來進行插值。其中權重的大小是根據空間自相關原理來確定的，插值誤差對空間位置有著較強的依賴關系。一般表達式為：

(1)

式中：Z(S0)為S0處的預測值；N為預測點使用的樣點的數量；λi為計算時用的權重；Z(Si)是在Si處獲得的真實值；P為指數值；di0是插值點S0與周圍已知點Si之間的距離。

(2)徑向基函數插值。徑向基函數插值法[9](Radial Basis Function，RBF)要求插值表面必須經過每個已知樣點。徑向基函數包括5種基本函數：線性函數、薄板樣條曲面函數、多項式函數、高斯曲面函數和立方體曲面函數。本文選取薄板樣條曲面函數模型進行試驗。

(3)普通克里金插值。普通克里金插值法[10, 11](Ordinary Kriging，OK)是建立在變異函數理論及結構分析基礎上的，在有限區域內對區域變量的取值進行無偏最優估計的一種方法。使用該方法需要先計算樣本變異函數；再根據變異函數選取變異理論模型，變異函數理論模型有球狀、指數、高斯、冪函數和空洞效應5種模型，具體選擇何種模型是由樣本變異函數決定；最后對未知點進行估計[12]。一般表達式為：

(2)

式中:Z(S0)為S0處的預測值；Z(Si)是在Si處獲得的真實值；λi為計算時用的權重，該系數是通過對樣本變異函數計算得到的。

(4)協同克里金插值。協同克里金法[13](Coordinative Ordinary Kriging，COK)是一種多變量估值方法，在普通克里金方法上，考慮不同變量之間的相關性，來提高估值的精度。該方法的關鍵是計算變量之間的協變異函數，一般表達式為：

γ12(h)=E{[v1(x+h)-v1(x)] [v2(x+h)-v2(x)]}

(3)

(4)

式中：vi(x)表示vi在x處的值；γ12(h)表示變異函數值；V(x0)為xi處的插值預測值；V(x1i)為各個點空氣濕度；V(x2i)在為各處的空氣溫度；λi為計算時用的權重，該系數是由協變異函數[式(3)]計算得到的。

(5)時空克里金插值。時空克里金法[14](Spatio-temporal Ordinary Kriging，STOK)是對普通空間克里金插值的時間維度擴展，為了處理時空數據，普通克里金法使用的固定模型不通用，需修改空間模型。本文采用的空間模型為時空分離模型，具體形式如下：

γ(hS,hT)=γS(hS)+γT(hT)+γST(hST)

(5)

式中：γS(hS)、γT(hT)和γST(hST)分別為空間、時間和時空變異函數；hS、hT和hST分別為空間、時間和時空的距離。

其中，時空距離考慮了時空幾何異向比率φ，故：

(6)

(6)時空-協克里金插值。時空-協克里金法(Spatio-temporal and Coordinative Ordinary Kriging，ST-COK)是以協同區域化變量理論為基礎，將其擴展到時間領域，探究同一時空域的多元時空結構現象的方法。其插值公式可以表示為：

(7)

式中：Z1(s,t)0為時空點(s,t)0處的空氣濕度；Z1(s,t)1i和Z2(s,t)2j為各個點的空氣濕度和溫度值；λ1i和λ2j為各個主輔變量的權重系數。

時空協變異函數是該方法的關鍵，它描述各個變量之間交叉的時空連續性。由于實際計算中，一般的計算方法較為復雜，因此使用一種新的變量方法來簡化上述計算過程[15]。新的表達式為：

(8)

新變量是將統一時空位置上的兩個變量的屬性值之和作為該位置的屬性值，從而簡化計算復雜度。然后，通過新變量變異系數與原始數據變異系數和協變異函數之間關系得出時空協變異函數，具體關系如下：

(9)

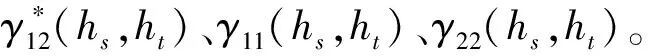
2.2 評價方法

為驗證不同插值方法在研究區域的預測精度，本文采用交叉驗證法來檢驗插值結果。在所研究區域樣本中，假設某一樣本點值未知，通過剩余樣本點值對其進行插值預測，利用預測的估計值與實測值的誤差來評價。本文主要采用平均絕對誤差(MAE)、平均相對誤差(MRE)和均方根誤差(RMSE)[16]。其中，平均絕對誤差反應模擬值的誤差范圍，平均相對誤差則反應模擬值對于觀測值的準確度，均方根誤差反應模擬值的靈敏度和極值情況。MAE、MRE和RMSE是插值精度的度量，其越小則說明插值方法越精確。此外，本文還針對每種插值方法計算其觀測值和模擬值的平均值、標準差及相關系數，以便于更全面的描述其插值結果的誤差情況。

(10)

(11)

(12)

3 實驗結果與分析

3.1 插值結果分析

為了直觀分析不同方法插值結果，本文以英特爾伯克利實驗室數據集中2月28日至3月28日的一個月濕度數據為例，根據不同方法插值得到濕度的空間分布圖如圖2所示，對比6種方法空間分布圖的直觀效果。

從圖2可知，每種方法都能從整體上反映出室內濕度的大致變化情況：總體呈現由左至右濕度逐漸增加，梯度變化較為明顯，不同插值方法所得結果在曲線平滑程度以及局部地區的空間分布存在一定差異：IDW法和RBF法的插值結果出現了明顯的“牛眼”，且圖像平滑性差；COK法、STOK法和OK法得到圖像較為平滑，其中COK法與STOK法更能體現具體的細節。所以采用COK和STOK法對室內濕度插值，能夠更加有效地避免出現誤差，結果也比IDW、RBF和OK法更精確。本文基于協同克里金和時空克里金插值法的基礎上，將兩者優勢進行結合形成ST-COK法，在上圖中顯示該方法也能夠得到平滑圖像和真實反應濕度的局部變化。

3.2 交叉驗證結果誤差分析

本文利用IDW、RBF、OK、STOK、 COK 和ST-COK插值方法，依次進行插值。其中，克里金使用了3種不同半變異模型(球形、指數和三次多項式)進行試驗，協同克里金采用高斯模型，IDW采用三次指數模型，RBF法使用薄板樣條模型。形成的濕度場誤差分析結果如表1所示。

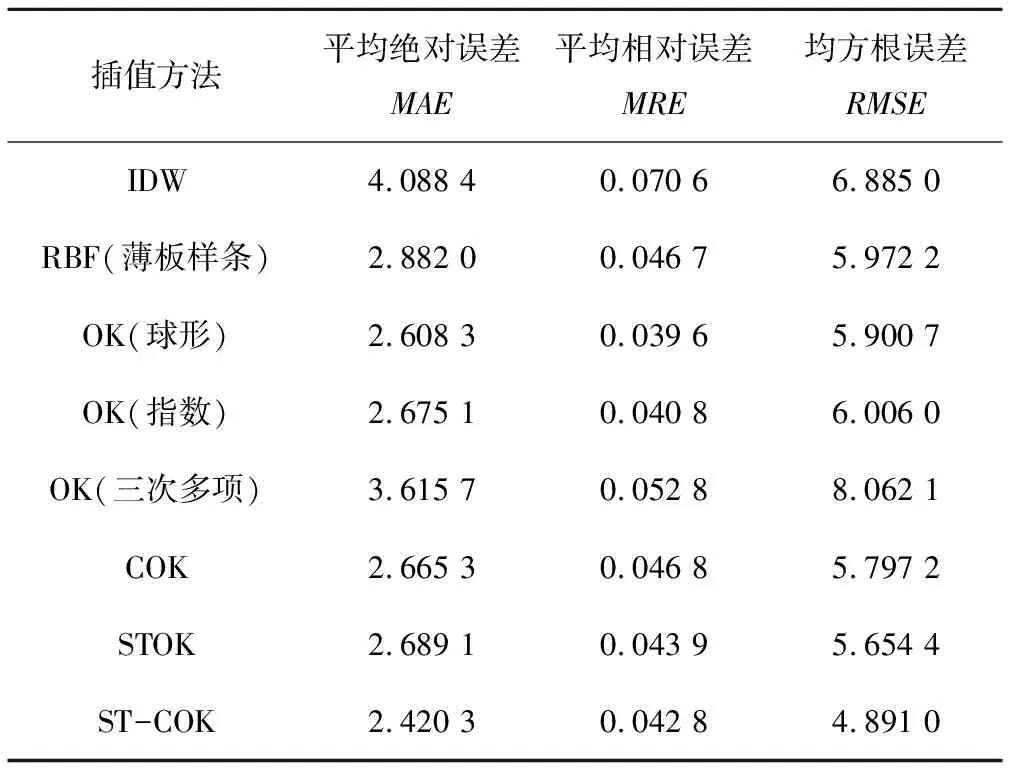
表1 6種插值方法的誤差指標Tab.1 Error indicators for 6 interpolation methods

由表1可知，不同插值法的交叉驗證結果表明：實測結果與預測結果均有顯著相關。就平均絕對誤差而言，ST-COK的預測誤差范圍最小，使用三次多項式的OK法的預測誤差最大，其余幾種方法基本接近，介于兩者之間；從平均相對誤差方面來看，整體波動很小，表明各種方法插值得到的數據可信度較高；從均方根誤差的數值分布來看，ST-COK的方法要優于其他幾種方法，表明該方法更接近觀測值數據。整體來看，ST-COK方法無論是在反應預測靈敏度與反應接近觀測值情況都要優于其他幾種方法，主要是由于其充分考慮了數據間的時空相關與屬性相關的特點。

圖2 基于不同方法的室內濕度場空間插值結果Fig.2 Spatial interpolation results of indoor humidity field based on different methods

3.3 其他參數的誤差分析

為了更加詳細的描述各種插值方法的預測結果的真實情況，本文還選取了觀測值與模擬值的極值、平均值、標準差以及相關系數等幾種參數作為進一步誤差分析的數據。

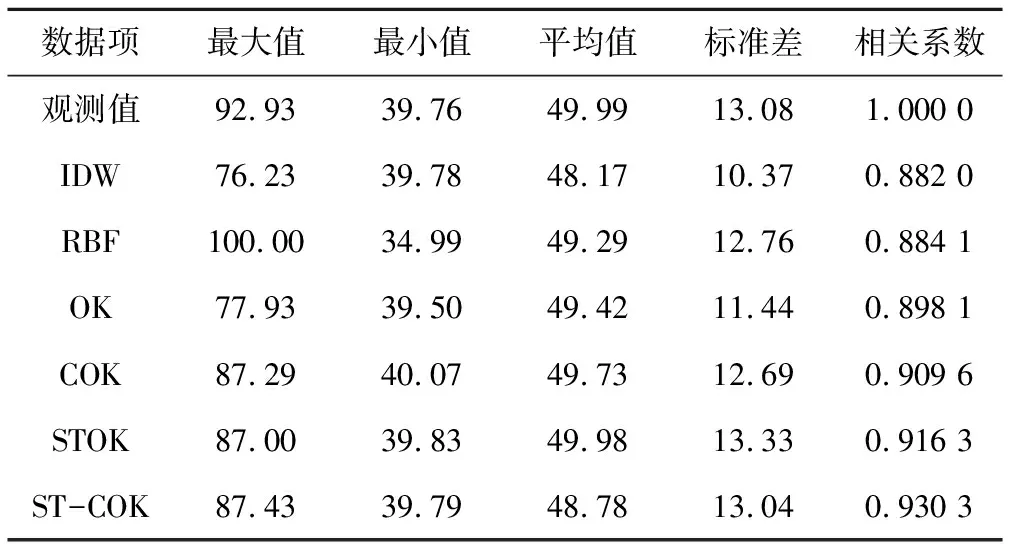
表2 6種插值法的預測值與觀測值比較 Tab.2 Comparison of observations and predicted values of 6 interpolation methods

由表2知，在極值方面，幾種改進的克里金方法預測出的極值與觀測值較為接近，在反應極值方面具有較大的優勢；在平均值方面，每種算法預測的結果與觀測值很接近，其中STOK的方法最優；在標準差方面，ST-COK方法最為接近觀測值；在相關系數方面，每種算法預測值與觀測值的相關系數都在0.8以上，表明模擬出的濕度場與真實情況較為接近，其中ST-COK方法的相關程度最高。故從整體方面來考慮，ST-COK方法在刻畫真實空間濕度場方面具有較好的能力。

4 結 語

本文使用物聯網與空間插值結合的室內濕度場模擬方法，避免了基于流體力學的建模精細程度高的問題。可以通過利用大量實時采集數據來插值得到整個室內的濕度場分布情況，為相關部門的研究提供參考數據與決策支持。

(1)從不同插值法空間分布圖來看，IDW方法與RBF方法能夠突出濕度場的局部變化，但是圖像不平滑，特別是在濕度變化的邊界會出現明顯的線條。OK、COK、STOK和ST-COK得到的圖像較為平滑，其中ST-COK方法可以更突出濕度場的局部變化，也相對的比較平滑。

(2)根據交叉驗證結果的分析，基于球形模型的OK方法與ST-COK方法模擬出的值誤差范圍最小；幾種方法模擬出的值準確度相差不大，其中IDW方法模擬值的準確度最低；ST-COK方法的靈敏度在幾種方法中是最優的。

(3)根據觀測值與模擬值的相關系數、均值和標準差等幾個參數分析。COK、STOK與ST-COK在反映極值方面和平滑作用具有顯著優勢，而IDW與RBF在這兩方面略顯不足；ST-COK方法模擬值與觀測值相關性最好，表明模擬結果的變化與觀測的變化具有一定的密切程度。

綜上所述，對于室內小尺度的濕度場模擬來說，ST-COK方法整體上要優于其余幾種方法。這是由于該方法充分考慮了數據間的相關聯度，從多個方面來約束預測數據的范圍。盡管這種方法能夠得到較好的模擬值，但需要的計算較為復雜，耗費大量的運算時間。此外，影響插值結果的準確性與傳感器位置和數量具有較大的聯系，這些問題有待進一步研究。