發動機氣門彈簧工藝參數調整

黃偉松，陳 浩，蔡麗紅，楊書偉，王以鵬

（上海工程技術大學 汽車工程學院，上海 201620）

氣門彈簧是內燃機配氣機構中氣門組件的重要組成部分，通過彈簧自身張力克服氣門關閉過程中氣門及傳動件因慣性力而產生的間隙，保證氣門及時落座并緊密貼合，同時也可防止氣門在發動機振動時因跳動而破壞密封[1]。而在實際氣門彈簧的生產過程中，無法對廢品彈簧進行及時有效的在線判斷，造成生產過程中的廢品率過高。因此，對于如何在線判斷廢品、判斷廢品的依據以及調整工藝參數的依據顯得尤為重要。而氣門彈簧的節距，是彈簧力學性能的重要參數[2]。同時，也是實際生產過程中需要控制的生產參數。它影響氣門彈簧的自由長度，從而直接影響彈簧的力學性能。但是，由于生產工藝的影響，實際生產過程中，彈簧節距值與理論設計值總存在一定的偏差。當超差量在一定范圍內時，不會影響到彈簧的合格率，同時能減少生產成本。本文著重分析節距偏差對彈簧總長的影響，建立不同偏差值的彈簧模型，對其進行仿真分析，以獲得能保證其使用性能的最大偏差量。

1 氣門彈簧的性能要求

氣門彈簧的基本參數是彈簧預緊力和彈簧剛度。氣門彈簧在疲勞壽命的使用范圍內，必須保證彈簧具有規定要求的彈性剛度，提供足夠的反力來平衡系統中氣門及其相關附件產生的各種力和慣性力，保證氣門閉合的力度和避免氣門飛脫[3]。同時，必須保證氣門彈簧的工作頻率和它的固有振動頻率不成整數倍關系，防止發生共振，使彈簧發生斷裂[4][8]。

氣門彈簧的使用過程中，由于受到壓縮載荷的作用，會產生并圈現象，這種自接觸行為會導致彈簧剛度呈非線性變化。在壓應力作用下，氣門彈簧會受到沿著45°方向的剪應力作用，最終導致疲勞斷裂[5]。因此，設計過程中，必須保證氣門彈簧的最大剪應力、米塞斯應力小于許用應力，其1階模態遠遠小于工作頻率。如下圖1所示。

圖1 氣門彈簧疲勞破壞圖

2 彈簧節距與自由長度的數模

在氣門彈簧的實際生產過程中，由于伴隨著節距誤差，彈簧的節距會逐漸增加。因此，彈簧的自由長度也會增加而偏離理論值。為了建立合適的節距——自由長度數學模型，測量了大量的彈簧實際節距，得到以下彈簧自由長度計算公式

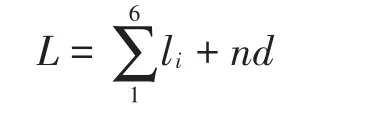
li是氣門彈簧在180度位置的實際測量高度，n和d分別表示氣門彈簧的圈數和氣門彈簧的鋼絲直徑。測量時，分別測量彈簧上下端面到中面的距離來減少測量誤差，然后對這些節距進行數據處理發現：

（1）規定氣門彈簧上、下偏差后，每個彈簧的節距值的變化趨勢一致。

（2）對于同一個彈簧，相鄰的三圈彈簧之間，測量出兩個不同的節距值。

3 氣門彈簧分析理論及CAD模型

3.1 分析理論

3.1.1 靜力學分析理論

氣門彈簧的靜力分析過程中，忽略了慣性力，及平衡方程中并沒有考慮了加速度的影響，因而整個系統控制方程為

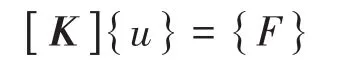
因此，結構靜力學問題，即歸結為求解靜力方程[6]。

3.1.2 模態分析理論

模態分析是分析結構自然頻率和模態形狀的方法，其在分析中會假設：

（1）結構剛度矩陣和質量矩陣不發生改變；

（2）除非指定使用阻尼特征求解方法，否則不考慮阻尼效應；

（3）結構中沒有隨時間變化的載荷。

在無阻尼系統中，結構振動方程如下所示

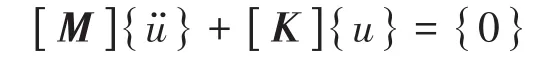
式中：[M]為質量矩陣；[K]為剛度矩陣；{}為節點加速度向量；{u}為節點位移向量。其中剛度矩陣可以包括預應力效應帶來的附加剛度[7]。

3.2 氣門彈簧CAD模型

實際生產過程中，彈簧的節距與理想的設計尺寸存在一定的誤差，因此，理想的彈簧設計模型與實際制造的彈簧模型存在一定的差別。其中，自由長度以及節距的差異性造成了實際生產的氣門彈簧與理論設計的彈簧的力學性能的差異。通過建立數學模型，可以發現實際生產過程中，氣門彈簧的自由長度超差量分別為正向超差、負向超差。某企業氣門彈簧生產過程中，允許的正負值超差量極值均為2 mm。實際生產中彈簧自由長度超差量越大，生產中的廢品率越高。為了找到正、負偏差量的極限值，同時驗證2 mm的超差量時，生產出的彈簧是否符合要求，分別在兩個極限范圍內設置不同超差量，實際自由長度超差量數值如表1所示：

根據實際彈簧的節距變化數據找到的數學模型，計算出每一圈彈簧節距相對于標準件彈簧的變化值，建立不同自由長度超差量氣門彈簧的CAD模型。氣門彈簧標準模型如下圖2所示。

圖2 標準氣門彈簧CAD模型

表1 彈簧模型超差量/mm

4 結果及分析

4.1 標準氣門彈簧性能

彈簧實際生產過程中，實際節距與理論值總存在一定的偏差，因此，彈簧的剛度和質量也會隨之變化，進而影響彈簧的振動特性。共振將導致配氣機構不能正常工作，氣門將發生沖擊和反跳，共振嚴重時甚至會導致彈簧斷裂。為了保證發動機運轉的平穩性和安全性，很有必要對氣門彈簧振動特性進行研究，避免發生共振[8]。彈簧自由長度越接近理論設計值時，彈簧力學性能越能滿足其工作需要。為了滿足彈簧性能要求，必須盡量減小超差值。然而，超差值越小，生產越困難，廢品率越高，生產成本越高，必須設置合理的超差值。因此，進行有限元仿真分析，比較超差模型和標準模型的剪應力、米塞斯應力以及彈簧1階模態的變化趨勢。

氣門彈簧在實際工況中會受到預緊力的作用，因此，本文在用ABAQUS軟件對氣門彈簧進行模態分析時采用預應力模態分析。提取最大剪應力、米塞斯應力以及預應力彈簧1階模態云圖。仿真結果表明最大剪應力和米塞斯應力位置在彈簧中圈內表面上，如圖3和圖4所示，彈簧1階模態如圖5所示。

圖3 標準彈簧最大Tresca應力

圖4 標準彈簧的米塞斯應力

圖5 標準彈簧1階模態

由仿真結果的中的最大Tresca應力可求出最大剪應力

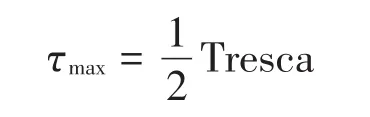
基于對有限元軟件求解結果的分析，得出標準氣門彈簧完全滿足力學性能要求。完全符合實際的工作狀況。

4.2 正偏差氣門彈簧性能

對于正向偏差量的彈簧，通過設置自由長度不同超差量，進行有限元分析，求解出每個模型的最大剪應力、最大米塞斯應力以及1階模態。并與標準件的最大剪應力、米塞斯應力以及1階模態比較，觀察自由長度的變化與各項性能的相對變化趨勢。如下圖6－圖8所示。

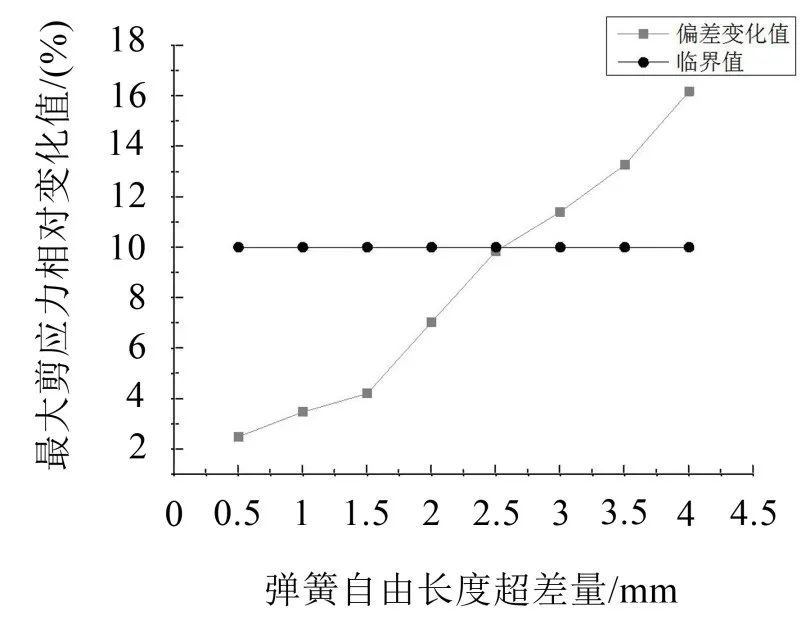
圖6 彈簧最大剪應力相對變化趨勢

通過Oringin Pro繪制彈簧最大米塞斯應力、剪應力以及1階模態相對標準件彈簧變化趨勢圖，可以更加直觀地分析彈簧的最大米塞斯應力、剪應力以及1階模態相對于標準彈簧的變化量。

（1）從上圖中我們可以看到，氣門彈簧偏差值2 mm在許用偏差范圍內，氣門彈簧的生產過程滿足彈簧性能要求。

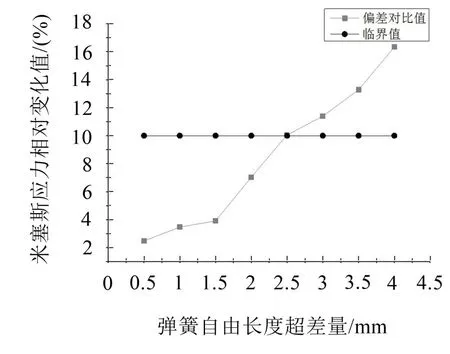
圖7 彈簧最大米塞斯應力變化趨勢

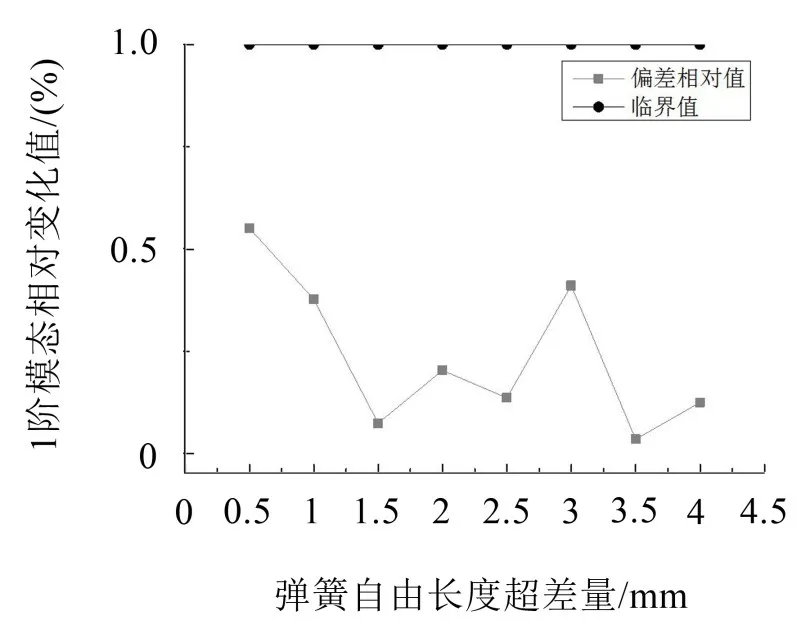
圖8 彈簧1階模態變化趨勢

（2）當彈簧自由長度正向逐漸增大時，彈簧的最大米塞斯應力、剪應力相對標準件彈簧應力值逐漸增大，盡管增大的過程中，有一些小的波動，但主體增長趨勢不變。

（3）可以觀察到彈簧自由長度變化量達到2.5 mm時，米塞斯應力的變化幅值超過了10%。因此，2.5 mm是偏差臨界值。

（4）當彈簧自由長度正向逐漸增大時，彈簧的1階模態與標準模型1階模態相比基本不變，超差量對其1階模態影響不大。

4.3 負偏差氣門彈簧性能

對于負值偏差量的彈簧，通過設置不同超差量，進行有限元分析，求解出每個模型的最大剪應力、最大米塞斯應力以及1階模態。并與標準件的最大剪應力、米塞斯應力以及1階模態比較，觀察自由長度的變化與各項性能的相對變化趨勢。如下圖9－圖11：

同理，通過Oringin Pro繪制彈簧最大米塞斯應力、剪應力以及1階模態相對標準件彈簧變化趨勢圖，可以更加直觀地分析彈簧的最大米塞斯應力、剪應力以及1階模態相對于標準彈簧的變化量。

（1）與正偏差結果相似，整體偏差值增大，自由長度也增加，彈簧的最大米塞斯應力、剪應力相對標準件彈簧應力值逐漸增大。

（2）當彈簧的自由長度變化，剪應力相對變化值和米塞斯應力的變化幅值并未超過臨界值10%，這表明預設的整體偏差值比較合理。

（3）當彈簧自由長度正向逐漸增大時，彈簧的1階模態與標準模型1階模態相比基本不變，超差量對其1階模態影響不大。

圖9 彈簧最大剪應力相對變化趨勢

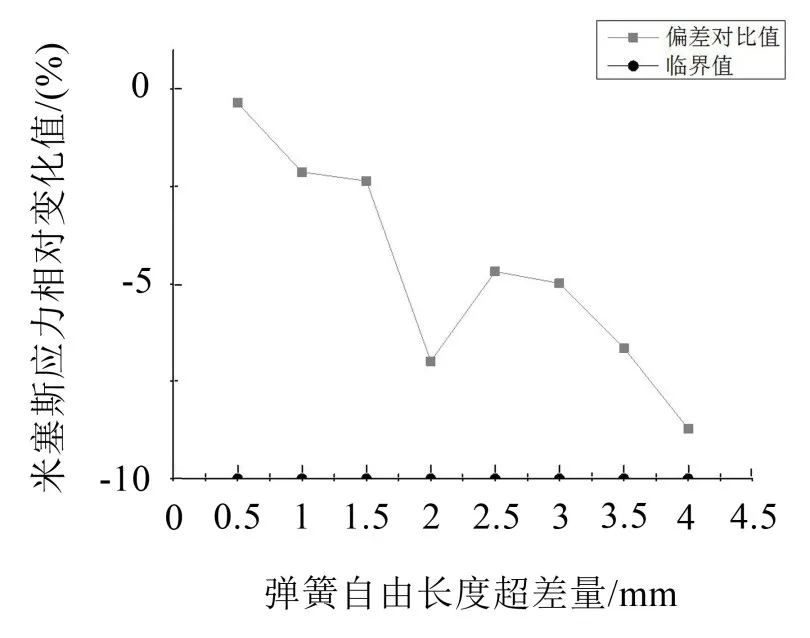
圖10 彈簧米塞斯應力相對變化趨勢

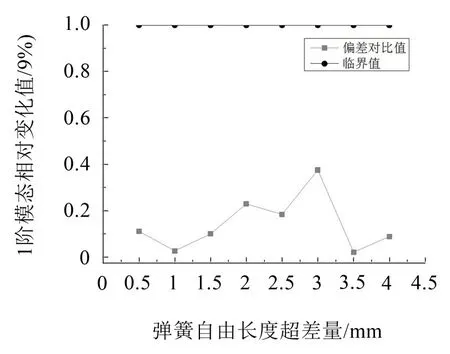
圖11 彈簧1階模態變化趨勢

5 結語

基于實驗和仿真研究，本文提出了調整氣門彈簧節距的方法，找到合適的偏差值以提高生產質量。其中，有限單元分析法用來確定彈簧整體的偏差預設值。正、負偏差條件下分別計算節距和彈簧整體自由長度的關系。在預設整體偏差條件下，這些規則可以運用于每個節距的調整，從而提高生產質量。建立標準CAE模型和正、負偏差的范圍。結果表明：

（1）最大米塞斯應力和剪應力隨著自由長度偏差量的增大而增大，氣門彈簧1階模態相對于標準模型的1階模態變化可以忽略。

（2）與標準彈簧模型相比，彈簧整體長度正偏差量不能超過2.5 mm，設置的所有負偏差量都滿足要求。因此，在彈簧制造生產過程中預設2.0 mm的偏差量是符合質量要求的。以后可以進一步實驗，對不同規格的彈簧進行研究，得到彈簧自由長度和許用超差量的關系，可以更快捷地得到不同彈簧在制造過程中可控制的超差量，以達到提高生產質量的目的。