改進傅里葉方法在梁結構振動特性分析中的應用

肖 偉，霍瑞東，李海超，高晟耀，龐福振

（1.中國艦船研究設計中心，武漢 430064；2.哈爾濱工程大學 船舶工程學院，哈爾濱 150001； 3.中國人民解放軍92578部隊，北京 100161）

梁結構在工程領域中應用廣泛，開展典型梁結構振動特性研究具有重要的價值。在此方面，Rao[1]得出了一般約束下Euler-Bernoulli梁的振動頻率和振型。ABBAS[2]使用有限元法求解得到了Timoshenko梁的自由振動方程。Grief[3]提出使用拉格朗日方程的基于傅里葉級數的振動模態方法。在此基礎上Chung[4]綜合利用傅里葉級數和拉格朗日乘子，提出了一種在經典邊界條件下梁的固有頻率和模態計算方法。W.L.LI[5]提出了一種改進傅里葉級數的方法，該方法在傳統傅里葉級數方法的基礎上增加了一項輔助多項式函數，成功解決了梁在邊界上存在的不連續性問題。張大克等[6]針對梁的振動方程采用了廣義差分法進行求解。許士菊等[7]采用有限差分法求解到了精度較高的振動模態數值解。曾文平等[8]則運用多辛算法推導求解了等截面梁的自由振動特性。

通過對國內外研究現狀的分析可知，現有的梁結構振動特性分析方法大多局限于經典邊界條件或某些特定的彈性條件，對一般邊界條件下的振動問題研究較少。為此，本文基于改進傅里葉級數法，建立了彈性邊界條件下梁結構振動分析模型，并基于彈簧參數法模擬一般邊界條件，在保證良好收斂性的前提下具有較高的求解精度，可為一般邊界條件下梁結構振動特性分析提供參考依據。

1 梁結構模型的建立與求解

在研究梁結構的彎曲振動問題時常用的物理模型主要有Euler-Bernoulli梁、剪切梁、Rayleigh梁和Timoshenko梁。其中，Euler-Bernoulli梁忽略了旋轉和剪切變形因素，剪切梁模型在其基礎上考慮了剪切效應，Rayleigh梁模型在其基礎上考慮了截面旋轉效應，而Timoshenko梁模型則同時考慮了旋轉和剪切這兩種效應，從而可得到最為理想的效果。

1.1 Euler-Bernoulli梁自由振動微分方程

本文取在一般邊界條件下的Euler-Bernoulli梁為研究對象，其物理模型如下圖所示

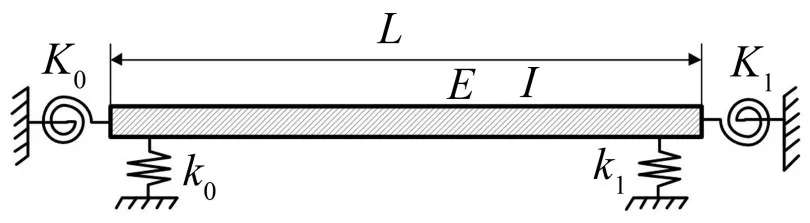
圖1 一般邊界條件下的梁結構示意圖

其中：K0、K1表示旋轉方向約束彈簧的剛度，k0、k1表示橫向約束彈簧的剛度。

根據彈性力學相關知識，梁的動力平衡方程可表示為

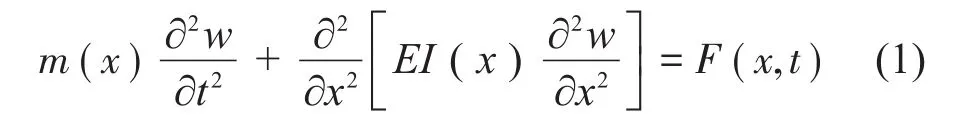
將梁視為均質等截面梁，在研究其自由振動時其外界激勵載荷F(x,t)=0，則上式可改寫為

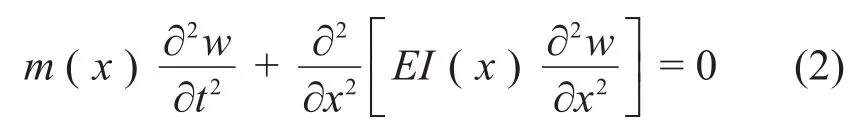
其中：I和E分別為梁的慣性矩和楊氏模量，w為梁的橫向位移函數。

梁結構的邊界條件可以表示為

其中：K和k分別代表旋轉約束和橫向位移約束彈簧剛度，通過改變彈簧剛度值可模擬不同邊界條件下梁結構的振動情形，具體彈簧剛度取何值能有效模擬各種邊界條件的討論將在后文進行。

1.2 基于改進傅里葉級數的梁結構振型函數

根據改進傅里葉級數的方法，Euler-Bernoulli梁的振型函數可表示為

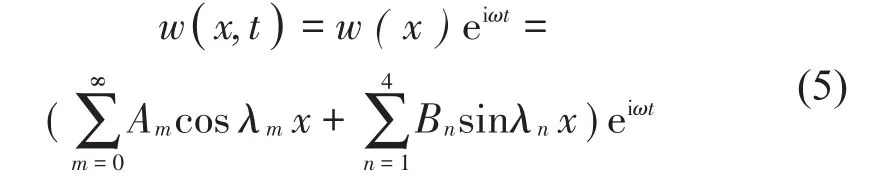
式中：Am和Bn是位移容許函數中未知的Fourier系數，λm=mπ/L，λn=nπ/L。引入簡諧時間因子eiωt用于表述梁在不同時刻的位移函數。顯然位移容許函數的選取將會直接影響到求解的結果，在求解過程中需將式（5）代入平衡方程式（1），但傳統傅里葉級數的導數在端點處會產生不連續現象，如圖2所示。

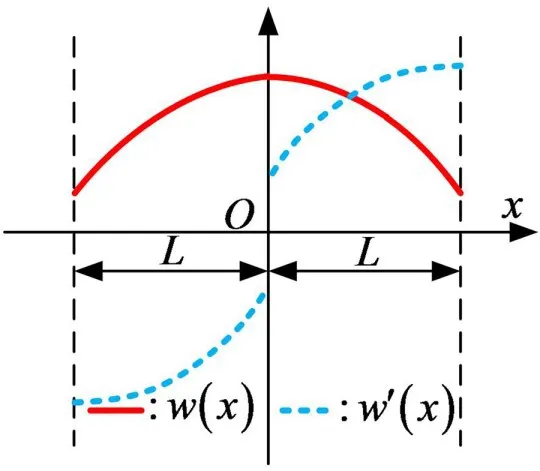
圖2 傳統傅里葉級數在端點處不連續問題示意圖

通過將位移容許函數表征為式（5）的形式，即除了單傅里葉余弦級數以外，還包含一項單傅里葉正弦級數，該正弦項輔助函數的引入使位移容許函數滿足求解域內2階導連續且3階導存在，從而有效地克服邊界上可能存在的不連續性問題，如圖3所示。

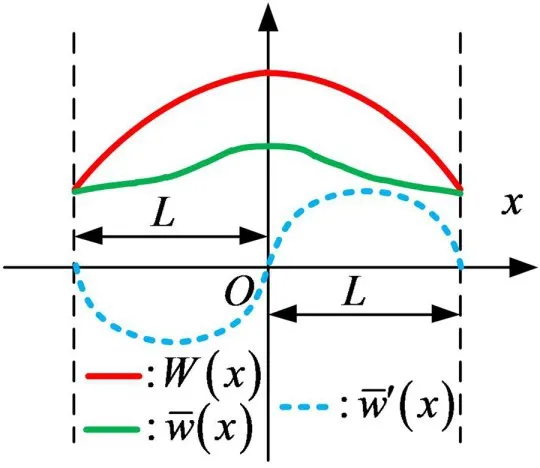
圖3 改進傅里葉級數解決端點處不連續問題示意圖

通過對位移函數逐次求導就可以得到速度、加速度等參數。因此整個求解過程的主要任務變為求解未知的傅里葉展開系數。

1.3 基于Hamilton原理的模型求解

首先對系統進行能量描述，分別求出該系統下的總勢能V、總動能T以及外部載荷做功We，然后基于Hamilton原理求解得到梁振動的特征值方程。由于Euler-Bernoulli梁是最簡單的梁結構模型，它忽略了旋轉和剪切效應，因而其彎曲產生的應變能可表示為

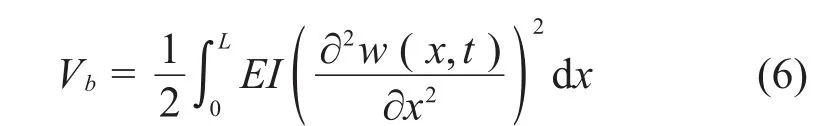
相應地，系統的動能Tb以及彈簧的勢能Vs可分別表示為

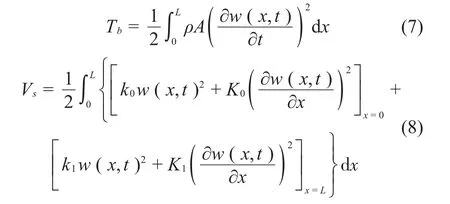
外部載荷所做的功可以表示為

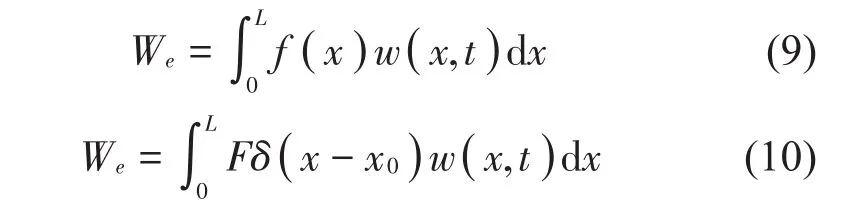
其中：外載荷為均布載荷時用式(9)表示，外載荷為集中載荷時由式(10)表示。δ為單位脈沖函數，F為外載荷的幅值，x0表示作用點的位置。

因此，總勢能可以表示為

于是，梁結構的拉格朗日函數可以表示為

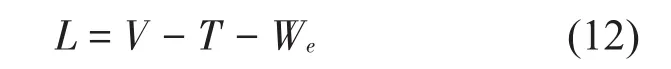
將式(6)－式(10)代入式(12)，并對未知的傅里葉系數求極值

聯立上述兩式，可得梁結構振動的標準特征式方程

式中：K和M分別為系統的剛度矩陣和質量矩陣，其取值只與系統的結構特征和邊界條件有關，當外載荷F=0時即可由求得梁結構自由振動下的振動特性。

任意激勵下梁結構的傅里葉系數向量可表示為

將上式求解結果代入式(3)，即可求得梁結構的受迫振動特性。

2 方法有效性驗證

為驗證本方法的收斂性和計算結果的準確性，本文從彈簧剛度值、傅里葉展開階數多個角度，定量分析影響本方法計算結果收斂性的因素。同時將本方法在幾種典型邊界條件下的計算結果與有限元計算結果及相關文獻進行比對。

本文所研究梁結構模型的幾何及材料屬性參數如下：長L=1 m，截面寬b=0.06 m，高h=0.01 m，楊氏模量E=2×1011Pa，密度ρ=7 800 kg/m3，無量綱頻率取Ω=L/π(ωρA/D)12。

2.1 彈簧剛度值對收斂性的影響

為了探討彈簧剛度k、K如何合理取值以模擬各種邊界條件，同時驗證彈簧剛度對計算收斂性的影響，圖4以C-C典型邊界條件為例，顯示了無量綱頻率參數Ω與彈簧剛度值的變化關系。其中假設K0=K1=k0=k1。

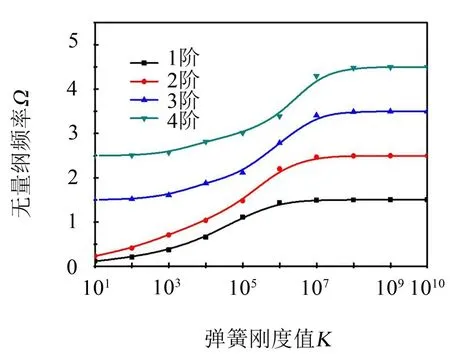
圖4 C-C邊界條件下Ω隨彈簧剛度值變化關系

從圖4可以看出，在C-C邊界條件下，無量綱頻率參數Ω在彈簧剛度取到1×108之后趨于收斂，此時即可模擬剛固的邊界條件，彈簧剛度在1×104～1×106區間內與頻率值大致呈線性關系，結合結構固有頻率應與材料彈性模量呈線性相關這一普遍規律，可將其視為彈性邊界條件。此外從上圖可以看出該范圍兩端的線性規律不如中間段明顯，因此彈簧剛度值取中間部分來模擬彈性邊界較為合理。如不做特殊說明，本文均取剛度值為1×1010來等效剛固條件，取1×105來等效彈性條件。在此基礎上，圖5討論了C-S邊界條件下，無量綱頻率參數Ω關于橫向彈簧剛度k1的收斂性。其中剛固端取K0=k0=1×1010，簡支端旋轉方向無約束，取K1=0。

從圖5可以看出，在C-S邊界條件下也有類似的規律，無量綱頻率參數Ω在彈簧剛度取到1×108之后基本趨于收斂，因此用旋轉方向彈簧剛度K=0、橫向彈簧剛度k=1×1010來模擬簡支條件是合理的。

為了探討上述用于模擬各種邊界條件所取彈簧剛度范圍和梁結構剛度之間的關系，本文以C-S邊界條件為例，給出了不同楊氏模量下1階固有頻率隨橫向彈簧剛度值k1變化的規律(見圖6)，其中剛固端取K0=k0=1×1010，簡支端取K1=0。

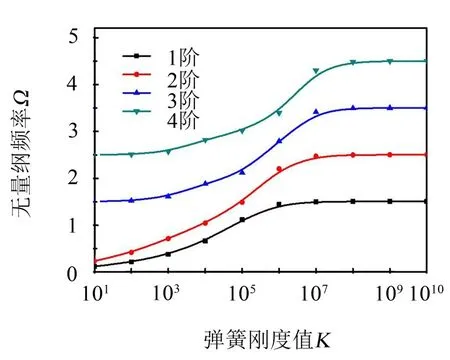
圖5 C-S邊界條件下Ω隨橫向彈簧剛度值k1變化關系

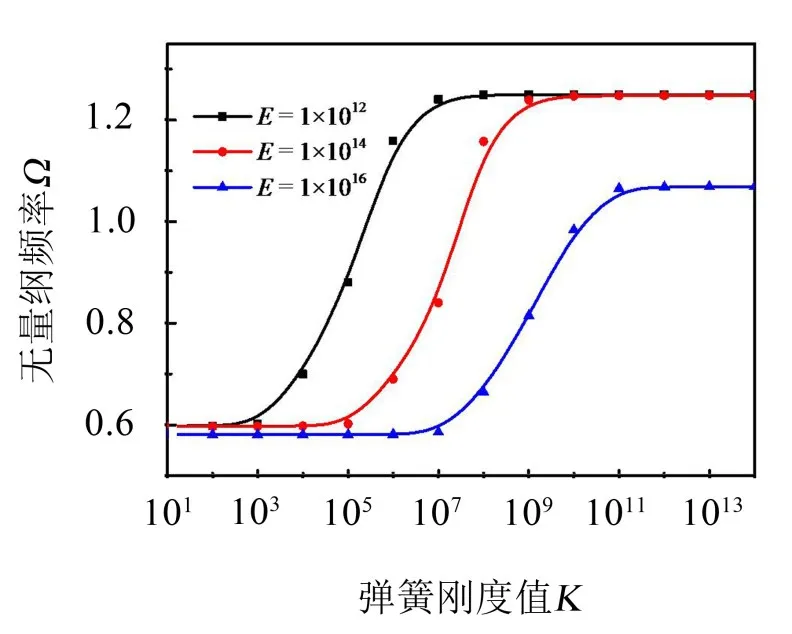
圖6 不同剛度下Ω隨橫向彈簧剛度值k1變化關系

從圖6可以看出，模擬不同邊界條件的彈簧剛度取值范圍與梁的剛度有明顯關系，梁的剛度越大，相應的線性范圍越靠右，即對于較大剛度的彈性梁應取較大的彈簧剛度值來模擬彈性邊界條件。具體范圍應通過試算來選取。

根據上述討論，本文給出了剛度取E=2×1011Pa時，幾種經典邊界條件下彈簧剛度的合理取值，如表1所示。

表1 彈簧剛度取值

2.2 傅里葉展開階數對收斂性的影響

傅里葉級數展開后所截取的階數對計算結果的精確度有直接影響，展開階數越多越接近準確值，但會影響求解效率。一般來說所取階數達到一定值后計算結果即可趨于穩定，本文以C-C邊界條件為例，探討了本方法計算結果收斂性隨展開階數M變化的影響。

從表2可以看出，隨著展開階數的不斷增加，梁結構無量綱頻率參數逐漸趨于收斂，當M=10之后無量綱頻率參數已具有較高的精度。因此本方法所求解的頻率值關于展開階數M收斂性良好，如不作特殊說明，本文展開階數均取M=10。

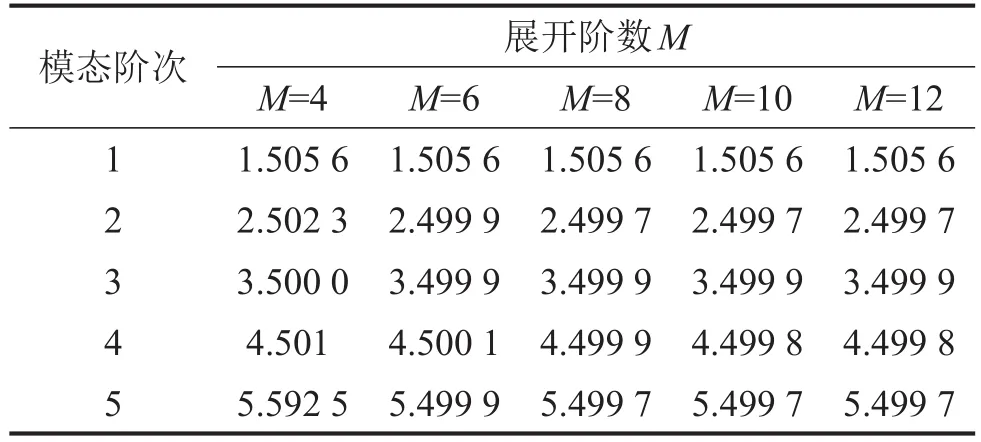
表2 C-C邊界條件下Ω與展開階數關系

2.3 有效性驗證

為了驗證本方法計算結果的有效性，本文給出了幾種典型工況下無量綱頻率的計算值，并與有限元仿真結果及現有文獻進行比對，有限元（ANSYS）分析模型參數與1.1節相同，單元類型為shell63，網格數量為47 926，對比結果如表3所示。

由表3可知，本文方法計算結果與有限元仿真結果具有較好的一致性，最大相對誤差不超過0.11%，由此可證得本方法的有效性；從計算效率上來看，本方法只需修改對應彈簧剛度值即可模擬各種邊界條件，在更換模型時只需修改對應尺寸參數與材料屬性值，可見本方法相較于傳統有限元法體現出了巨大的優勢。本方法所求得C-C邊界條件下梁結構自由振動振型圖與有限元仿真對比如圖7所示。

3 簡諧載荷作用下的受迫振動響應

在對梁結構進行一般邊界條件下自由振動模態分析的基礎上，討論了一定激勵下結構的受迫振動響應特性。

其中梁的具體參數保持不變，激勵載荷幅值取F＝1 000 N，掃頻范圍取f＝1 Hz～1 000 Hz。圖8和圖9分別給出了梁在剛固和彈性邊界下梁中點位置處速度與加速度級的響應曲線，其中模擬彈性邊界條件下的彈簧剛度值取：K0＝K1＝1×105N·m/rad，k0＝k1＝1×104N/m。

由圖6可知，彈性邊界條件下梁結構的波動程度比剛固邊界條件大，尤其是在低頻激勵下這種情況更為明顯，但相應的激勵響應幅值卻要小很多，此規律可為工程中的減振方案提供借鑒與參考。

為探討彈性邊界條件下旋轉方向約束彈簧與橫向約束彈簧剛度變化對梁振動特性的影響程度的區別，本文給出了一些對比性的數值結果。表4為對梁一端剛固，另一端分別改變旋轉方向和橫向彈簧剛度后梁的1階無量綱頻率值。

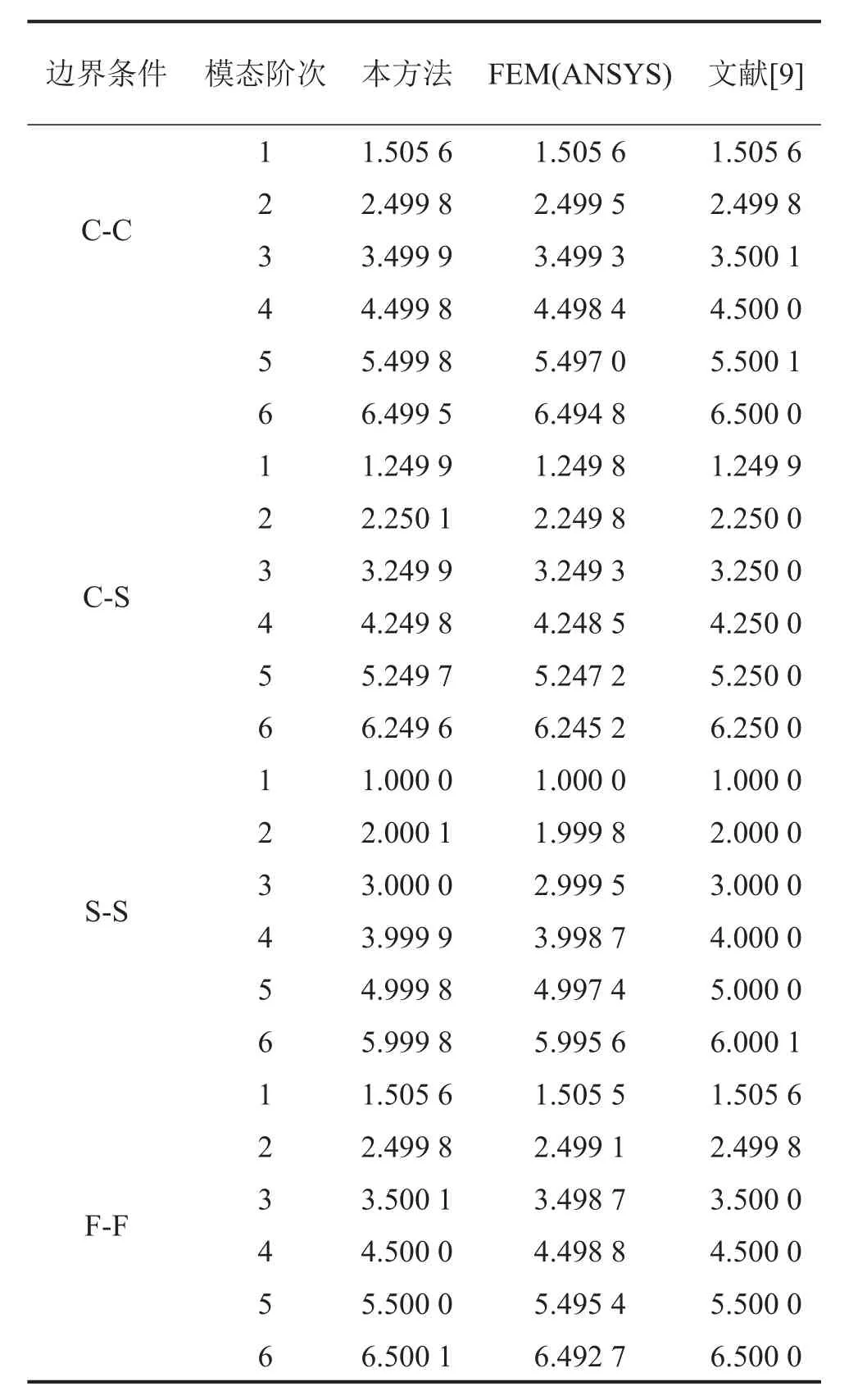
表3 經典邊界下梁結構的無量綱頻率參數

將表4的數值結果用三維圖表示如圖10所示。

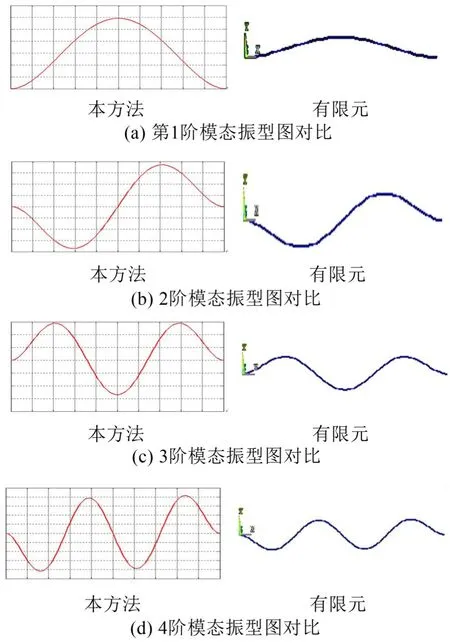
圖7 C-C邊界條件下本方法與有限元結果振型圖對比

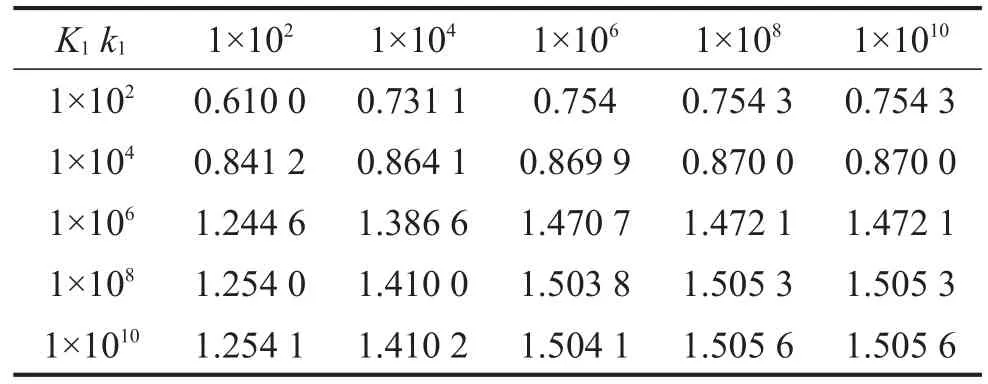
表4 旋轉方向和橫向彈簧剛度變化對固有頻率的影響

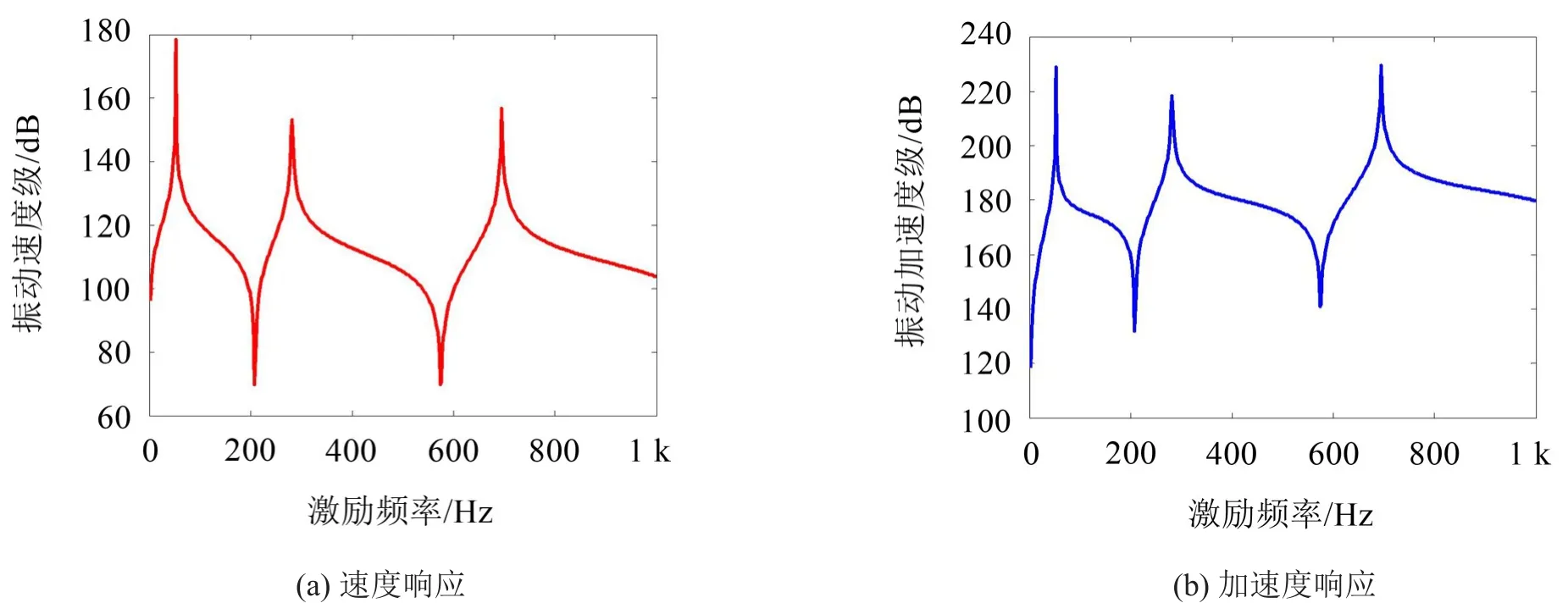
圖8 剛固邊界條件下梁中點位置處激勵響應圖

從圖10中可以很直觀地看出兩者對梁振動特性影響程度的不同。當橫向彈簧剛度k保持不變時，1階無量綱頻率隨旋轉方向彈簧剛度K的增大變化不很明顯，而當旋轉方向彈簧剛度K保持不變時，1階無量綱頻率隨橫向彈簧剛度k的增大變化很大，由此可知橫向約束對梁結構振動特性的影響起主要作用。

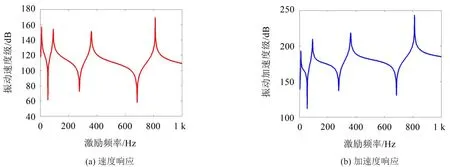
圖9 彈性邊界條件下梁中點位置處激勵響應圖表1經典邊界下的彈

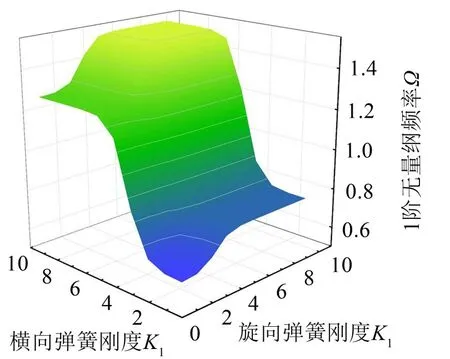
圖10 旋轉方向與橫向彈簧剛度對固有頻率值的影響

5 結語

本文基于改進傅里葉級數法對一般邊界條件下梁結構的振動特性進行了研究，通過本文研究，可得如下主要結論：

(1)通過計算分析并與有限元結果對比驗證了改進傅里葉級數法的準確性與良好的收斂性。

(2)通過改變結構兩端的彈簧剛度值可有效模擬一般邊界條件，并給出了典型邊界條件下彈簧剛度的合理取值。

(3)模擬不同邊界條件彈簧剛度值的選取取決于梁的剛度值大小。

(4)針對梁的低頻受迫振動，對梁進行彈性約束可更有效降低結構的振動響應。

(5)在彈性邊界條件下，梁端橫向約束對結構振動特性的影響比旋轉方向約束大。