白砂糖電導灰分測定結果的不確定度評定

平秋婷，王桂華，張志強，余構彬，高裕峰

（1廣東省生物工程研究所（廣州甘蔗糖業研究所） 廣東省甘蔗改良與生物煉制重點實驗室，廣東廣州510316；2國家糖業質量監督檢驗中心，廣東廣州510316）

0 引言

制糖生產過程中，從原料到成品糖除含有蔗糖、還原糖外，還含有非糖物，非糖物中的無機成分對制糖過程及產品影響極大。因此，測定原料和成品糖中的灰分，掌握其變化規律，用以評價工藝條件的控制，改進生產管理，提高產品質量都具有重要意義[1]。電導灰分作為白砂糖分級評定的一項重要指標，其測量的準確性顯得尤為重要[2]。本文依據新實施的國家標準GB/T 35887-2018《白砂糖試驗方法》[3]，采用電導率儀法測定白砂糖的電導灰分，找出影響測定結果的不確定度的因素，通過建立數學模型對各個不確定度分量進行評估和合成，最終合成了相對標準不確定度和擴展不確定度。

1 材料與方法

1.1 實驗儀器與設備

電子天平（精確至0.01 g），梅特勒-托利多（儀器）上海有限公司；DDSJ-308F電導率儀，上海儀電科學儀器股份有限公司；100 mL容量瓶（A級）。

1.2 實驗試劑

去離子水，0.0025 mol/L氯化鉀標準電導率溶液。

1.3 實驗方法

稱取白砂糖31.3 g±0.1 g于潔凈燒杯中，加入去離子水溶解并移入100 mL容量瓶中，用去離子水多次沖洗燒杯及玻璃棒，洗水一并移入容量瓶中，加入去離子水至標線，搖勻。先用0.0025 mol/L氯化鉀溶液校正電導率儀，用樣液沖洗測定電導率用的電導電極及小燒杯2～3次，然后倒入樣液，用電導率儀測定樣液電導率，記錄讀數時的樣液溫度，計算結果。

2 數學模型的建立

式中：X─電導灰分（g/kg）；Ci─313 g/L 糖液在20℃時經水溶液和溫度校正后的電導率（μs/cm）；n─重復實驗次數。

3 不確定度來源分析

測量不確定度是表征合理地賦予測量之值的分散性，與測量結果相聯系的參數[4]。測量不確定度一般由若干分量組成，該分散性主要涉及A類不確定度、B類不確定度和合成標準不確定度：①A類不確定度：用對觀測列進行統計分析的方法，用標準偏差表征，來評定標準不確定度；②B類不確定：用不同于對觀測列進行統計分析的方法，也用標準偏差表征，來評定標準不確定度；③合成標準不確定度：當測量結果是由若干個其他量的值求得時，按其他各量的方差和協方差算得的標準不確定度[5]。

根據數學模型和測量過程，白砂糖電導灰分的不確定度來源包括（如圖 1所示）：①樣品質量引起的相對標準不確定度 urel（m），主要來源于電子天平的精度；②樣品定容引入的相對標準不確定度urel（V），主要來源于容量瓶精度和環境溫度；③重復測量引入的相對標準不確定度 urel（ci），主要由操作人員的操作水平高低決定；④電導率儀精度的相對標準不確定度urel（P），主要來源于電導率儀的精度。

4 不確定度分量評定

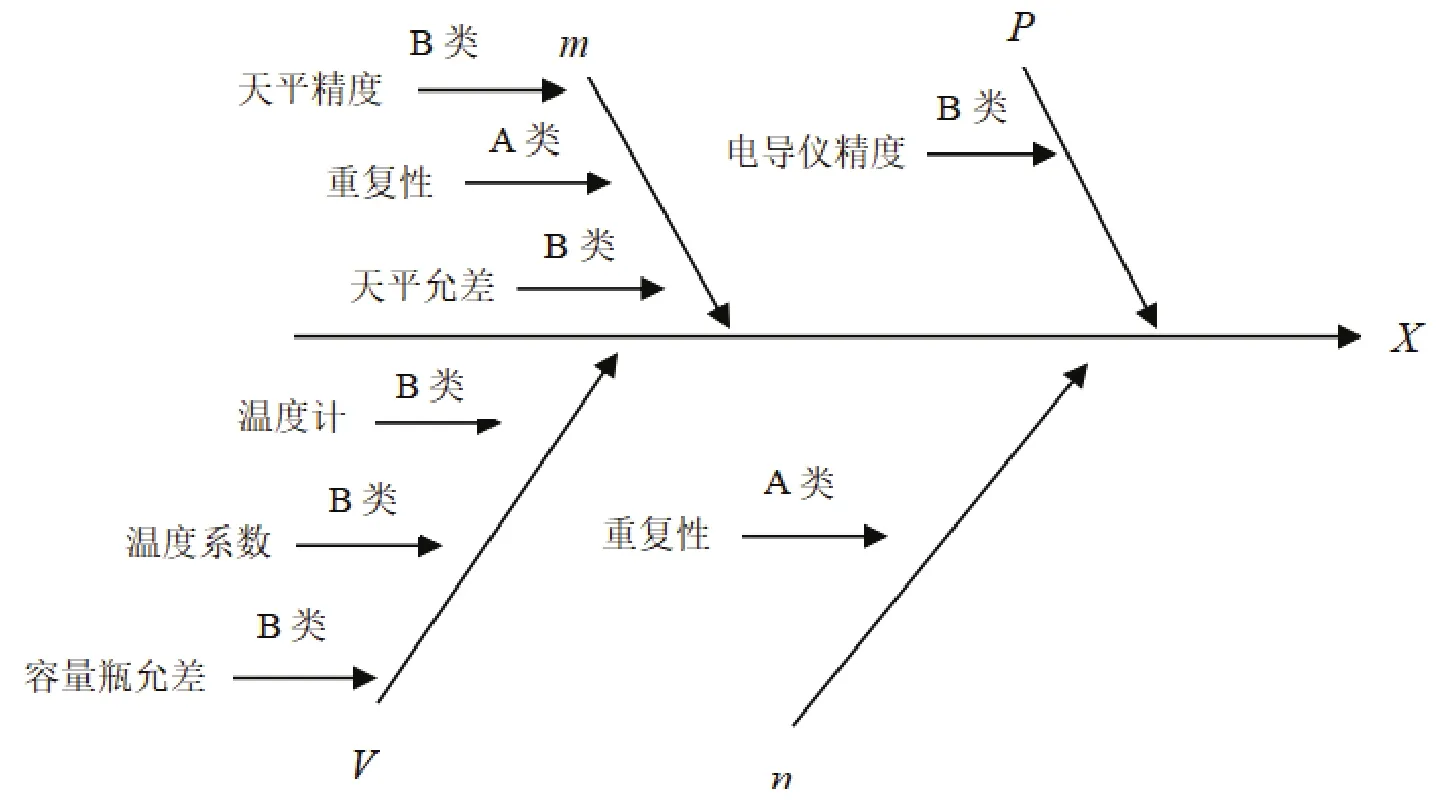
圖1 白砂糖電導灰分的不確定度來源

4.1 樣品質量引起的相對標準不確定度urel（m）

質量m不確定度來自3個方面：第一，稱量的重復性，可以通過10次重復測量，采用 A類評定方法求出；第二，由天平稱量不準引入的不確定度，按B類方法評定；第三，天平標度的可讀性（數字分辨力），按B類方法評定。

4.1.1 重復性引入的標準不確定度分量uA（m）

對質量m進行重復10次的測量，測量結果見表1。采用貝塞爾公式計算標準不確定度uA（m）為：

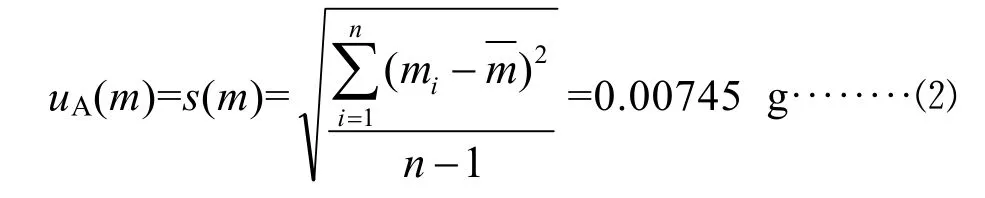
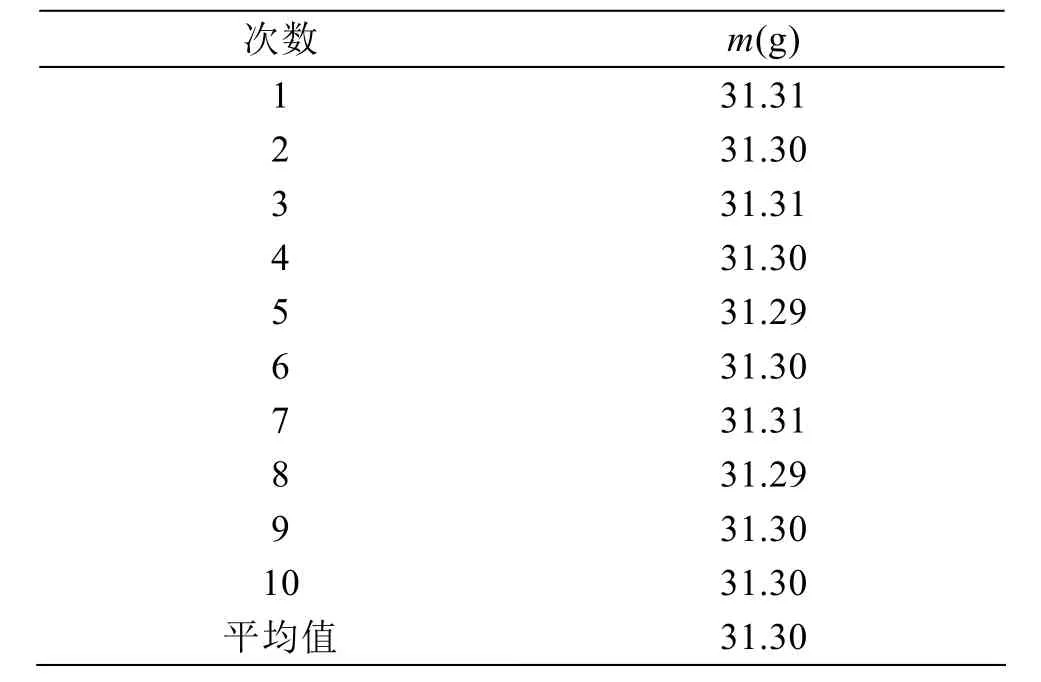
表1 樣品質量10次重復測量結果

4.1.2 天平允差引入的標準不確定度分量uB1（m）

電子天平的最大允差為±0.1 g，則區間半寬度a1（m）=0.1 g，假設m測量值落在該區間的概率分布為均勻分布，包含因子k1（m）=3，因此標準不確定度為：

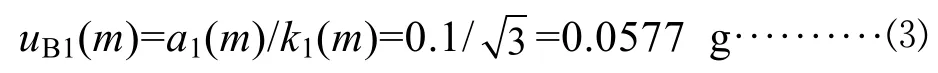
4.1.3 天平分辨力引入的標準不確定度分量uB2（m）

數字式測量儀器對示值量化（分辨力）導致的不確定度服從均勻分布。天平分辨力為 0.01 g，區間半寬度 a2（m）=0.01 g，包含因子 k2（m）=因此標準不確定度為：

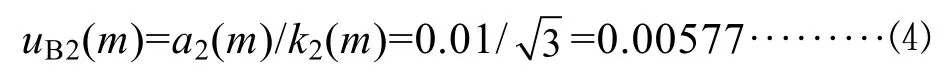
4.1.4 質量m的合成標準不確定度uc（m）和相對標準確定度 urel（m）

上述3個分量相互獨立，互不相關。因此合成標準不確定度為：

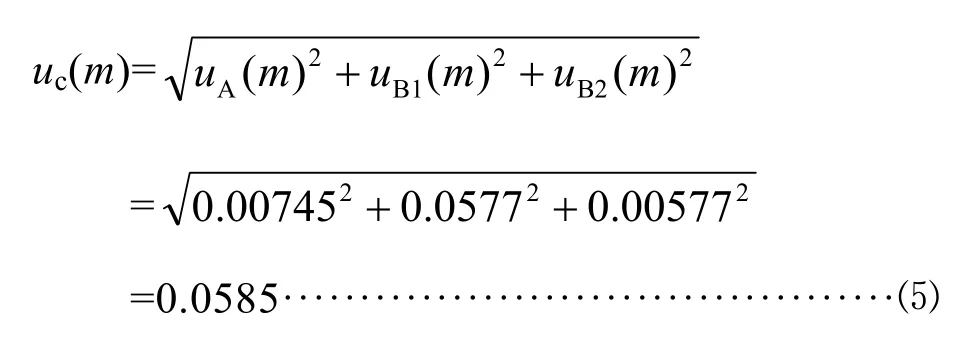
其相對標準不確定度為：

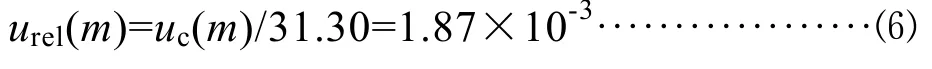
4.2 樣品定容引入的相對標準不確定度urel（V）

樣品定容引入的不確定主要來源于2個方面：最大允差和溫度影響，兩者均按B類方法進行評定。

4.2.1 容量瓶允差引入的標準不確定度分量uB1（V）

A級100 mL容量瓶的允差為±0.1 mL[6]，則區間半寬度 a1（V）=0.1 mL。在沒有給出置信水平或分布的情況下，假設其服從三角分布，則包含因子

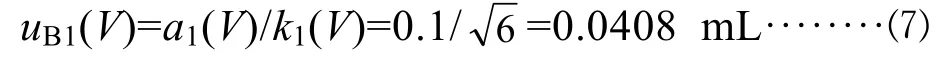
4.2.2 溫度系數引入的標準不確定度分量uB2（V）

容量瓶的檢定或校準一般是在室溫20.0℃環境條件下進行的[3]，本研究在 25.0℃條件下進行。水的體積膨脹系數為2.1×10-4/℃，產生的體積變化為±（100×5×2.1×10-4）=±0.105 mL，將其設為均勻分布，其標準不確定度為：

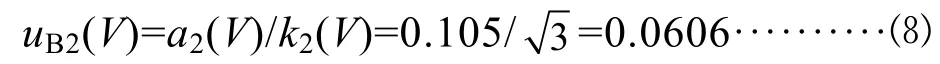
4.2.3 玻璃溫度計校準引入的標準不確定度分量uB（t）

根據玻璃溫度計校準證書上顯示的溫度最大允差為±0.20℃，則區間半寬度 a（t）=0.20℃，在 95%的置信區間中，假設其服從均勻分布，則包含因子因此其標準不確定度為：

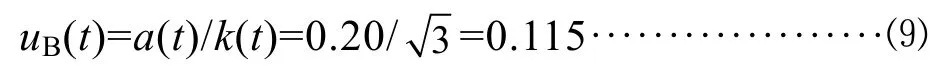
4.2.4 樣品定容引入的合成標準不確定度 uc（V）和相對標準不確定 urel（V）因此其標準不確定度為：

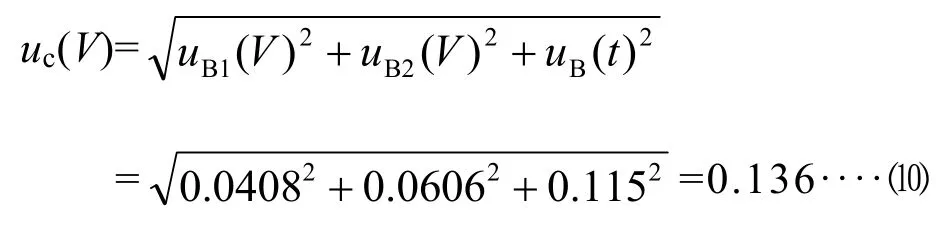
其相對標準不確定為：

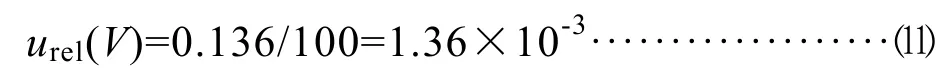
4.3 重復測量引入的相對標準不確定度urel（ci）

對同一白砂糖樣品重復測定10次，結果見表2。

采用貝塞爾公式計算，求得單次測量標準差s（ci）為：

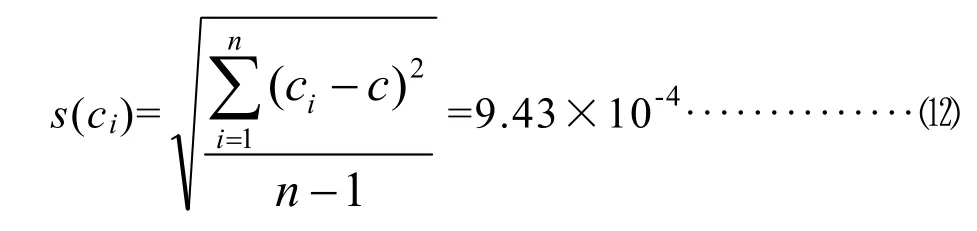
由測量重復性導致的標準不確定度u（c）為：

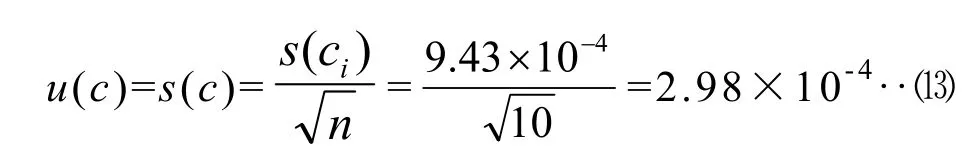
因此，重復測定的相對標準不確定度為：

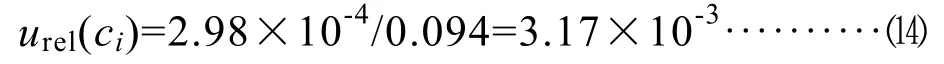
4.4 電導率儀精度的相對標準不確定度urel（P）

儀器檢定證書給出儀器的總體擴展不確定度U（P）=0.3%，則區間半寬度為 a（P）=U（P）=0.3%；樣品的電導灰分在20℃測量平均讀數為16.00 μs/cm，服從正態分布，在置信區間 95%，則包含因子k（P）=2，其相對標準不確定為：

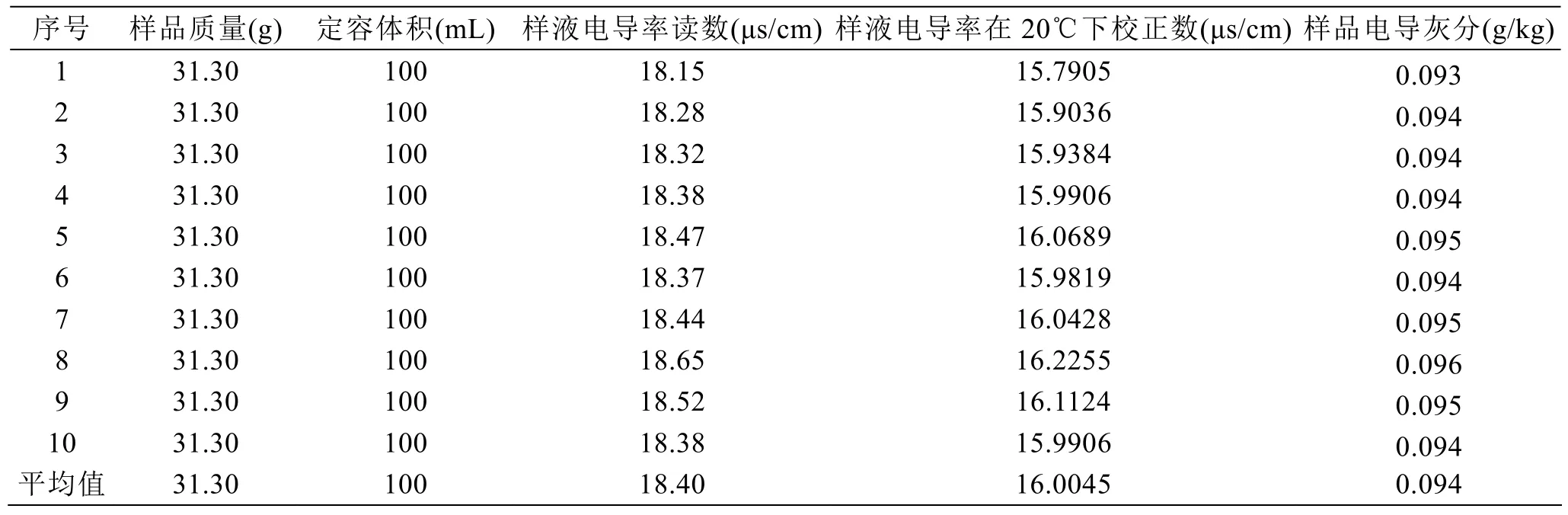
表2 白砂糖樣品電導灰分測定結果

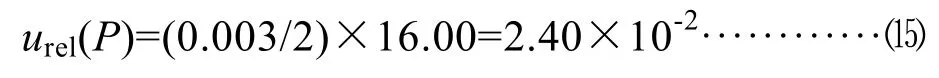
4.5 計算合成相對標準不確定urel

各個不確定度分量計算值如表3所示。

合成相對標準不確定為：

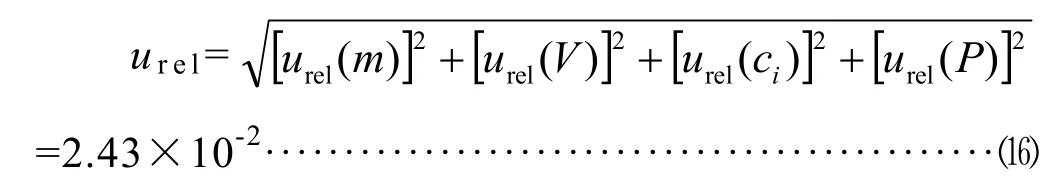
4.6 擴展不確定U

表3 白砂糖電導灰分測定相對不確定分量評定結果

由表1可知，白砂糖樣品的電導灰分平均值為0.094 g/kg，其合成標準不確定度為 u=2.43×10-2×0.094×100%=0.23%，在95%置信水平下，包含因子取k=2，擴展不確定為：U=ku=0.46%，實際白砂糖樣品的電導灰分測定結果可表示為：0.094±0.0046 g/kg。

5 結論

采用電導率儀法測定白砂糖電導灰分的過程中，影響測定的不確定度主要來源于樣品質量、樣品定容體積、重復測量和電導率儀精度4個方面引入的不確定度分量。在現有實驗條件下，測定結果的標準不確定度為 0.23%，在 95%置信水平下，擴展不確定為：U=0.46%，實際白砂糖樣品的電導灰分測定結果可表示為：0.094±0.0046 g/kg，滿足白砂糖電導灰分檢測的標準要求。