基于稀疏解組合優化的廣義重心坐標

彭豐富，方 明

?

基于稀疏解組合優化的廣義重心坐標

彭豐富，方 明

(桂林電子科技大學數學與計算科學學院，廣西 桂林 541004)

根據廣義重心坐標線性運算的性質與特點，運用廣義重心坐標的稀疏解權函數的調和平均組合方法，對空間凸多面體頂點設計了一種求解廣義重心坐標的算法，且權函數是帶有保形參數的一元函數，因而具有保形優化的特點。構造了2種不同類型的帶形參權函數，運用不同權函數及其參數的廣義重心坐標將平面圖形映射到空間曲面的實例進行了分析，并應用重心坐標常用的等值線工具對保形性進行了比較。

廣義重心坐標；稀疏解；組合優化；權函數

M?BIUS[1]于1827年首先提出了位于三角形內任一點的重心坐標的概念，即該點表示為相應3個頂點的加權系數為該點的重心坐標。通過對頂點加權方法可以推廣到任意多邊形，稱之為廣義重心坐標(generalized barycentric coordinate，GBC)。GBC在有限元計算、網格編輯、計算機圖形學等有著廣泛的應用，由于GBC的不唯一性，從而不同的方法所計算的重心坐標有差異。目前，主要有多種基于平面多邊形提出的方法，并一直在發展、應用這些理論，同時也有一些新的方法在不斷提出。

1976年WACHSPRESS[2]首次提出了第一種建立在任意凸多邊形的GBC：Wachspress coordinates (W坐標)，其計算量較小，得到了如仿射不變形、光滑性等較好的性質，其不足是不能處理非凸多邊形。1995年ECK等[3]基于能量最小原理提出了離散調和(discrete harmonic)的GBC，其與W坐標有許多相似性質，但不要求坐標的非負性。2003年FLOATER[4]提出了均值廣義重心坐標，其可以對任意多邊形計算重心坐標，可以為非凸的，且不要求坐標非負。2004年馮結青和趙豫紅[5]分析和比較了各種重心坐標的定義方法，提出一種魯棒的均值重心坐標計算方法，并從理論和實驗兩方面證明了均值重心坐標在多邊形邊界上的拉格朗日性質和線性性質。2005年谷留新和劉克軒[6]將改進的均值坐標應用于平面多邊形的變形，提出一種基于多邊形星形分解的同構三角網格剖分算法，選用較少的額外點降低了算法復雜度。2015年DENG等[7]對于Floater提出的四邊形的廣義重心坐標族的極限給出了證明。2016年CHEN和GOTSMAN[8]提出由于調和坐標一般沒有封閉的形式，因此必須通過求解一個關于域的離散化的大型線性方程進行數值逼近。2016年FLOATER[9]又研究了凸多邊形中常見的幾種廣義重心坐標的單調性，并發現這些GBC有共同的簡單的單調性：與一個頂點相關的坐標函數沿著多邊形邊界到此頂點的任意直線遞增。áKOS[10]對W坐標、調和坐標及均值坐標3種GBC方法做了詳細地闡述，并運用等值線作為工具進行了比較。

上述GBC方法的提出主要針對平面多邊形，并且都是基于點線面之間的距離、面積、角度等尺度關系來構造權系數，優點是其幾何意義明顯，缺點是難以做到保形及形狀調配和優化。近二十年，該方法又被推廣到空間多面體領域。2007年JU等[11]對Mean value坐標進行了拓展，推廣應用于3D四面體及高維單形多面體的研究。2011年WACHSPRESS[12]對運用W坐標構造有理基函數應用于多邊形和四面體做了相應的研究和總結。2013年GUESSAB[13]對任意凸多面體應用重心坐標得到的一元凸函數進行了逼近分析。本文基于四面體的仿射變換應用重心坐標對曲線曲面的構造也得到了一些結論[14-16]。

本文基于GBC本身的代數性質來構造其計算方法，使得重心坐標的計算回到其向量運算的本源，并對該方法進行算法優化，同時考慮基于保形的坐標優化。

1 稀疏解組合廣義重心坐標

1.1 單形的稀疏解

其中，≥0，由于重心坐標的規范性，其可以等價于[n]=(0,1,···,–1,+1,···,)T。因而式(1)等價于

1.2 單形的選取準則

在R3中設計了如下的最簡單形取法和求解稀疏解：

輸入：空間數據點{}，；

輸出：最簡單形{}，稀疏解。

步驟1.=0={}(=1,2,···,)；

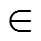
步驟2.3. 若步驟2.2中的假設不成立，擴充到0中尋找，找到可能重復的2，3，同樣得到非零數為4的稀疏解；

步驟2.4. 否則為邊界面上的內點，由={,1,2,3}確定非零數不超過3的稀疏解；

步驟3.={}，重復步驟2。

圖1 R3中最簡單形選取方法

2 稀疏解的組合

對于GBC的連續性有如下定理。

權函數u()的選取目標是使得GBC變換對曲線具有保形性，譬如將一條平面線段通過GBC描述到一個曲面上，理想的保形是確保映射到曲面的是一條測地線，由于其優化計算過于復雜，一般也可以通過能量最小的方法進行優化處理。對單形()的u()計算時，選取()的幾何重心與的距離d(V())作為參數來進行優化，直觀地理解是u()應該隨d的增大而減少，也就是單形的重心與越近，該單形占有權重越大。其函數關系如一些文獻選取概率密度函數或其他的遞減函數。可從計算的角度及重心坐標的性質出發，構造二者的2個實驗函數

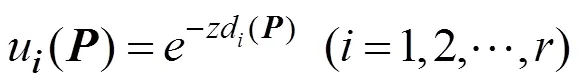
3 實例分析

從圖中可以看出，前者參數具有較好的保形性和等值曲線的光順性，而后者保形性和光順性都比較差，其原因是權重函數的遞減速度太快，導致圖形某些方向的收縮過大，從而導致等值曲線的曲率急速增大。

圖2 式(4)參數(x,y)=(2,0)將平面圖形映射到曲面

圖3 式(4)參數(x,y)=(1,2)把平面圖形映射到曲面

圖4 式(5)中z=1的平面圖形映射及等值線

圖5描述的是不同權函數關于d的變化情況。

圖5 不同權函數ui (P)關于di的變化情況

4 結束語

為了求解空間廣義重心坐標，根據廣義重心坐標本源的線性運算性質，運用稀疏解權函數組合的方法，對空間凸多面體頂點構造了一種求解重心坐標的方法，且能選擇參數對保形效果進行優化調配。在實例中的等值線均為離散的點，所以未考慮先插值再計算曲率進行對比，從實例的計算結果也驗證了方法的可行性。對非凸情形本文未考慮，若是取消重心坐標的非負性，方法應該可以推廣。

未來工作的展望主要包括：①對GBC變換的保形性可以用直線映射到測地線為目標的優化方法來研究，但是計算量可能會相當大；②對光滑曲面的映射保形可以選用連續的帶參數的概率密度函數作保形優化處理，已有文獻對連續閉合曲線的情形給予了討論，但是對空間閉合曲面還有一定的挑戰；③設計自適應的方法來保形優化，而不是對全局進行參數優化，雖然會增加計算量，但是在細節上可以得到更好的效果。

[1] M?BIUS A F. Derbarycentrischecalcul [D]. Leipzig: Nabu Press, 2010.

[2] WACHSPRESS E L. A rational finite element basis [J]. Journal of Tribology, 1976, 98(4): 635.

[3] ECK M, DEROSC T, DUCHAMP, et al. Multiresolution analysis of arbitrary meshes [C]//In SIGGRAPH ’95: Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM Press, 1995: 173-182.

[4] FLOATER M S. Mean value coordinates [J]. Computer Aided Geometric Design, 2003, 20(1): 19-27.

[5] 馮結青, 趙豫紅. 均值重心坐標的魯棒算法及其幾何性質[J].計算機輔助設計與圖形學學報, 2004, 16(6): 772-776.

[6] 谷留新, 劉克軒. 改進的基于Mean value重心坐標的多邊形變形[J]. 計算機工程與應用, 2005, 41(29): 74-76.

[7] DENG C Y, SHI F F, LIU J Z. The limit of barycentric coordinates for quadrilaterals [J]. Computer Aided Geometric Design, 2015, 38(C): 38-39.

[8] CHEN R J, GOTSMAN C. On pseudo-harmonic barycentric coordinates [J]. Computer Aided Geometric Design, 2016, 44(15): 15-35.

[9] FLOATER M S. On the monotonicity of generalized barycentric coordinates on convex polygons [J]. Computer Aided Geometric Design, 2016, 42: 34-39.

[10] áKOS T. Comparison and affine combination of generalized barycentric coordinates for convex polygons [J]. Annales Mathematicaeet Informaticae, 2017, 47: 185-200.

[11] JU T, LIEPO P, WARREN J. A general geometric construction of coordinates in a convex simplicial polytope [J]. Computer Aided Geometric Design, 2007, 24(3): 161-178.

[12] WACHSPRESS E L. Barycentric coordinates for polytopes [J]. Computers and Mathematics with Applications, 2011, 61(11): 3319-3321.

[13] GUESSAB A. Generalized barycentric coordinates and approximations of convex functions on arbitrary convex polytopes [J]. Computers and Mathematics with Applications, 2013, 66(6): 1120-1136.

[14] CHEN J J, PENG F F. Approximate spline of G2-continuity on a generalized hyperbolic paraboloid [J]. Journal of Computational and Applied Mathematics, 2013, 248(2): 99-117.

[15] PENG F F, HAN X L. Parametric splines on a hyperbolic paraboloid [J]. Journal of Computational and Applied Mathematics, 2009, 229(1): 183-191.

[16] PENG F F, CHEN J J. Spline on a generalized hyperbolic paraboloid [J]. Journal of Computational and Applied Mathematics, 2011, 235(8): 2451-2458.

Generalized Barycentric Coordinates Based on Combinatorial Optimization of Sparse Solutions

PENG Feng-fu, FANG Ming

(School of Mathematics and Computing Science, Guilin University of Electronic Technology, Guilin Guangxi 541004, China)

According to the nature and characteristic of the linear operation of generalized barycentric coordinates, by means of a combination of weighted harmonic mean funcitons, an algorithm for solving generalized barycentric coordinates is designed to meet the demands of the vertexes of spatial convex polyhedron, in which the weighted function is a unary function with conformal parameters, thus it is characterized with conformal optimization. Two different types of weighted functions are constructed in this paper, and they are both used to calculate the generalized barycentric coordinates. An example of a plane figure is mapped into a space surface by the means, which is to be described and analyzed with different weighted functions and parameters. By means of their contours, the generalized barycentric coordinates for the example are analyzed and compared.

generalized barycentric coordinates; sparse solution; combinatorial optimization; weighted functions

TP 391

10.11996/JG.j.2095-302X.2019010054

A

2095-302X(2019)01-0054-05

2018-06-18；

2018-06-28

國家自然科學基金項目(1170119)；廣西高校數據分析與計算重點實驗室項目

彭豐富(1972-)，男，湖南婁底人，博士，副教授。主要研究方向為計算機輔助幾何設計。E-mail：pengfengfu@aliyun.com