長距離跨海地鐵隧道定向誤差分析及應用

胡玉祥，陳鵬，尹相寶，張洪德，孟慶年

(1.青島市勘察測繪研究院，山東 青島 266032； 2.青島市西海岸基礎地理信息中心有限公司，山東 青島 266000)

1 引 言

隨著社會經濟的發展，各城市紛紛掀起了建設地鐵的熱潮，而地鐵施工通常由若干車站相連接，車站間距離通常較短，而對于較長的區間，通常在車站間建立風井將區間進行聯測，以此提高導線精度。青島地鐵1號線全長 59.9 km，橫穿膠州灣海底，跨海長度 3.5 km，需要建設海底隧道，依次連接黃島區和青島市區，而按照傳統方法無法通過中間建立風井的方式聯測，因而如何將高精度的地面值引入地下，對于地鐵1號線海底隧道的順利貫通具有重要意義。本文采用雙導線的形式通過斜井將地面觀測值引入地下，分析了影響測量精度的主要誤差源，最后給出了具體的應用建議。

2 誤差理論分析及應用

青島地鐵1號線跨海段由膠州灣兩端斜井相向開挖，黃島段薛家島設兩座施工斜井，市區段團島設一座施工斜井，高程可采用高精度電子水準儀通過斜井導入，因而如何導入高精度的平面坐標和方位是關鍵。黃島段開挖進度較快，在入海口處建立一座風井，將斜井與風井進行聯測，以便建立高精度的入海起始坐標和方位，入海隧道建立雙導線網，增加檢核條件，提高精度。故涉及的主要誤差源有：兩井定向誤差(入海口起始方位角和坐標誤差)、地下導線測量誤差。

2.1 兩井定向測量

兩井定向測量和一井定向一樣，由投點、井上連接和井下連接3個部分組成[1]。井下連接導線某一邊方位角總誤差為：

(1)

式中θ為投向誤差[1]。但由于兩井定向垂球線間距離很大，投向誤差對定向精度的影響已經很小了，暫不考慮。

(1)井上連接誤差

兩井定向時，井下連接導線某一邊的方位角按下式計算：

(2)

式中：αAB——兩垂球線的連線在地面坐標系統中的方位角；

式(2)中僅方位角αAB與地面連接有關，故地面連接誤差m上=mαAB。

圖1 兩個近井點的兩井定向地面連接

如圖1所示，假定AB邊所在直線為y軸，垂直于AB的方向為x軸。則方位角αAB的誤差為[2，3]：

當近井點S和T位于AB線的同側時，有：

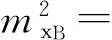
+b2(R(T-B)x+R(S-A)x)2

當近井點S和T位于AB線的異側時，有：

(3)

式中mxα01、mxα2——近井點S和T處的起始方位角中誤差引起的A、B垂球線在x軸上的誤差；

mxS、mxT——近井點S和T的x坐標誤差。

(2)井下連接誤差

圖2 兩井定向的井下連接導線

如圖2所示為井下連接導線圖，共測了n-1個角和n個邊。井下連接誤差是由井下導線的測角誤差mβ和量邊誤差ml所引起的。即：

(4)

根據相關微分、積分公式[3]可推得地下導線第i條邊的方位角誤差和邊長誤差為：

(5)

(3)應用建議

兩井定向誤差中的井上連接誤差由式(3)知，其主要受近井點起始方位和坐標精度的影響，對于地鐵施工認為近井點精度較高，故而其影響較小。而井下連接誤差由測角誤差和量邊誤差組成，量邊誤差主要與井下導線的長度有關，由于邊長測量較易控制，所以重點研究測角誤差。依據(5)式可知，測角誤差與導線邊數、導線形狀等有關，對于等邊直伸形導線，測角誤差可簡化為：

(6)

假設現有n=7個邊的井下直伸形連接導線，測角中誤差為1″，依據式(15)可得到每條邊的方位角誤差，如表1所示。

方位角誤差關系表 表1

從表1和以上公式可知，用近似直伸導線做井下連接時，各邊的連接誤差以起始邊和最終邊為最大，由兩端向中間，各邊方位角誤差成對稱分布并以此減小，中間邊為最小。所以在有條件的情況下，入洞導線起始邊最好布設成兩井定向的中間邊。

2.2 地下導線測量

(1)導線誤差分析

地下工程地下平面控制測量通常采用支導線形式。通過對測角和測距誤差分析[3]可以看出，由于測角量邊誤差的積累，必然使導線點位位置產生偏差，從而產生貫通誤差。如圖3所示，1、2、3、…導線點的點位沒有誤差，1′、2′、3′、…導線點是在測角量邊誤差影響下各相應導線點的位置。

圖3 井下支導線誤差

設β1、β2、…、βn為所測導線的左角；l1、l2、…、ln為導線的邊長；α1、α2、…、αn為導線邊的坐標方位角；mβ1、mβ2、…、mβn為導線角度的誤差；ml1、ml2、…、mln為導線邊長的誤差。

支導線終點K的坐標可按下式確定：

(7)

而導線邊的坐標方位角是所測角的函數，即：

(8)

由此可見，導線終點的坐標是整個導線所測角度和邊長的函數，因而導線終點坐標的誤差公式為：

(9)

上式等號右邊第一項為測角誤差對終點坐標的誤差影響，第二項為量邊誤差的影響。

(10)

圖4 Ri及其在坐標軸上的投影

設Ri為導線終點與某一導線點連線長度，Ryi為Ri在y軸上的投影(如圖4所示)，則：

(11)

將以上各式帶入式(8)可得：

(12)

式中：Rxi—導線終點與各導線點的連線長度在x軸上的投影。

將以上各式帶入式(8)可得：

(13)

當等精度測角時可得：

(14)

(2)精度指標確定

依據式(14)可知，邊長測量誤差主要與導線的形狀、終點距起始點距離有關，而角度測量誤差源較復雜，對地下導線測量的影響較大，當地下導線敷設為近似等邊直伸形支導線時，式(14)可簡化為

(15)

假設地下導線的長度為2 km、地下導線測量中誤差 ≤±30 mm，依據式(14)可得到導線邊長、測站數以及測角中誤差之間的關系，如表2所示。

導線邊長、測站數和測角中誤差的關系 表2

從表2可以看出當導線邊長不超過 150 m、測站數超過14時，測角中誤差應≤1.36″，依據規范[6]，測角宜采用0.5″級全站儀按4個測回進行施測、測距宜采用I級(1 mm±1 ppm×D，D為邊長，以km為單位)以上測距精度按2個測回進行施測。

3 工程實例分析

青島地鐵1號線過海段是連接黃島和城區的關鍵環節，過海段在黃島側設立兩座施工斜井，在市區段設立一座施工斜井，由兩側對向開挖，目前由黃島側已開挖 3 425 m，距離貫通面還有 78 m。在黃島入海處設立了一座施工風井，由2#斜井和風井進行了兩井定向，入海起始邊盡量布設在兩井定向地下導線的中間位置，確定入海起始方位和坐標，然后采用雙導線形式進行地下控制點聯測。為滿足要求，采用徠卡TS50測量機器人(標稱精度：±0.5″、0.6+1×D，D為邊長，以km為單位)測量角度、距離，角度測4個測回、距離對向觀測2個測回，對地下導線進行了相關測量工作。

本文首先進行兩井定向并分析誤差確定起始方位和起始坐標，然后采用雙導線進行聯測，進行整體平差，在此基礎上對雙導線進行了精度分析并給出具體的使用建議，如圖5所示。

圖5過海段長距離定向測量示意圖

(1)斜井導線測量與兩井定向測量對比分析

首先通過斜井采用雙導線的形式測得地下起始方位邊WGDXY01-WGDXY02-1(方案一)，然后采用斜井和風井的兩井定向形式測至地下起始方位邊WGDXY01-WGDXY02-1(方案二)，分別經過平差計算，同時采用陀螺儀加測起始方位邊(方案三)，得到三者的對比如表3所示。

地下起始方位角對比 表3

通過對比可知，方案二與方案三起始邊方位角相差較小，而單純采用雙導線推求的地下起始方位角(方案一)與其余兩種方式相差較大；而對于邊長測量，方案一與方案二幾乎無差別。

(2)起算點對斜井導線測量的影響分析

在青島城市坐標系下，y坐標分量是橫向誤差的直接體現，對于相同的外業觀測數據，起算數據不同，對比最弱點的y坐標分量。

起算方位變化影響 表4

如表4所示，起算方位變化對地下起始方位邊的影響近似常數，對最弱點的影響呈一定的倍數關系。

(3)雙導線和支導線對比分析

通過對比分析，雙導線方向觀測值和邊長觀測值明顯增多，提高了布網的網形強度，有利于增加檢核條件，在一定程度上提高導線測量的精度，如表5所示。

不同導線布設形式對比 表5

4 結 論

作為國內第一條跨海地鐵線路，如何保證青島地鐵1號線長距離跨海段的順利貫通意義重大，本文通過具體數據分析驗證了雙導線應用于長距離跨海隧道定向測量中的優勢，通過分析長距離隧道定向測量的誤差源，從理論上解釋了影響長距離隧道定向的主要因素，對于長距離跨海隧道定向測量具有一定的參考價值。

本文主要形成以下幾個使用意見：

(1)對于長距離隧道，若條件允許，可以通過增加豎井的形式進行聯測，提高導線測量的精度；有條件的地方最好將入洞起始邊布設為兩井定向的中間邊。

(2)通過布設交叉導線(雙導線)形式，雖然外業觀測量增大，但增加了多余觀測，利于發現錯誤，增加檢核條件，一定程度上提高導線測量的精度。

(3)雙導線從本質上講仍舊是支導線，隨著距離的增加，測角和測邊對導線測量的影響變大；同時與導線的形狀有一定關系，直伸導線影響大，曲折形導線影響小。

(4)對于長距離隧道定向測量，起算點的影響對導線各點的影響為常數，不隨導線的增長而增大。

(5)對于地下導線測量，可以通過加測陀螺邊提高定向測量的精度。