基于結構相似性的非參數貝葉斯字典學習算法

董道廣，芮國勝，田文飚，康健，劉歌

（海軍航空大學信號與信息處理山東省重點實驗室，山東 煙臺 264001）

1 引言

字典學習是圖像和通信信號處理方面的重要內容，是進行信號和圖像數據分類[1]、壓縮[2-6]、去噪[7-11]、修復[7,9-10,12-13]乃至超分辨[14]的有力工具，隨著我國太空戰略的深入推進，字典學習在海洋信息感知領域，尤其在衛星圖像遙感、衛星氣象遙感、衛星軍事偵察等方面的應用價值愈發凸顯。近年來，非參數貝葉斯方法在字典學習中的應用引起人們的關注，相對于以最優方向法（MOD, method of optimal directions）和K奇異值分解算法（K-SVD，K-singular value decomposition）為代表的傳統綜合字典學習算法體現出了顯著的優越性。該優越性體現在三方面：1）學習過程中能夠自動推斷出字典原子數目、信號稀疏度和正則化參數值，從而無需對這些參數的取值進行預設，避免了因預設不當而造成的人為影響；2）有嚴格的理論證明其算法的收斂性和解的最優性，而K-SVD和MOD尚缺乏理論證明的支撐；3）其自身基于概率圖模型進行建模，結構清晰且具有開放性，適于引入各種正則化概率先驗約束。

Zhou等[11]將非參數貝葉斯用于圖像去噪和壓縮重構，提出了 beta過程因子分析（BPFA, beta process factor analysis）算法，是貝葉斯因子分析方法在字典學習領域的一次成功嘗試，取得了較好的應用效果，但該算法沒有考慮到圖像的全局結構相似性和變異性，在字典結構特性方面仍有較大提升空間。后期圍繞提升非參數貝葉斯字典學習的結構特性，又陸續出現了狄氏過程-beta過程因子分析（DP-BPFA，Dirichlet process-beta process factor analysis）[7]和相依分層 beta過程（dHBP，dependent hierarchical beta process）[9-10]等算法，這些算法將空間相關性引入了非參數貝葉斯建模，使圖像在字典學習下的稀疏表示能夠體現出一定的鄰近空間相似性，顯著提升了字典在去噪、修復、壓縮感知等方面的應用性能，但復雜度頗高，運行時間較長。Sunil[15-16]及 Li[17-18]等認識到結構相似性和變異性對信號/圖像稀疏表示的重要影響，基于狄氏過程的聚類特性，提出了適于多來源數據條件下的多字典學習算法，較好地解決了圖像稀疏表示對結構相似性的利用問題。但數據聚類的先驗建模用到了stick-breaking模型，因其非共軛的數學形式，造成了后驗推斷上的非解析性。其次，多字典學習適于數據來源非單一的情形，對于單一來源數據內部結構的聚類效應，其適用性仍值得進一步研究。在傳統的結構字典下，圖像的稀疏表示具有塊結構性，這利于提高字典對信號結構特征的表達能力，且相似圖像塊稀疏表示的支撐集通常也相似，利于進行多觀測向量模型下的聯合稀疏重構，進而利于降低觀測數目并提高重構性能。這為非參數貝葉斯字典學習提供了重要的啟發，即將字典學習建立在圖像塊相似性聚類的基礎上，并進一步將塊結構特性引入稀疏表示作為字典學習的正則化約束條件。而非參數貝葉斯字典學習則因其對圖像本身結構的自適應性，繼續保持其相對于傳統結構字典的優勢。

本文在上述問題和解決思路的啟發下，提出了一種基于結構相似性的非參數貝葉斯圖像字典學習算法，其主要創新有三方面：1）以圖像塊的相似性為測度，通過K-均值分類算法對圖像塊進行聚類處理，將前述各非參數貝葉斯字典學習算法的空域結構特征從局部擴展到全局，使所有具備相似結構的圖像塊共同參與本聚類圖像塊的稀疏表示；2） 鑒于傳統結構字典下多個相似信號聯合稀疏重構時一般假設支撐集相同的局限性，為使相似圖像塊的稀疏表示適應支撐集平滑變化的實際情況，令同一聚類內部的各圖像塊對字典原子的使用僅服從概率意義上的相同，使得學習所獲得的字典利于進行多信號的聯合稀疏重構；3）將傳統結構字典下信號稀疏表示普遍存在的塊結構效應作為正則化約束條件引入非參數貝葉斯字典學習框架，以提升字典對圖像結構的表達能力。

2 貝葉斯建模

2.1 基于全局結構相似性的圖像預處理

圖像內部存在大量的相似冗余成分，其在傳統結構字典下的稀疏表示也具有相似性，突出體現為支撐集的相似性。將全局相似性測度引入字典學習框架有利于提升字典對圖像結構特征的表達能力。本文采取K-均值聚類方法進行圖像塊聚類。K-均值聚類是一種簡單而又行之有效的無監督聚類方法，在數據未分類亦無標簽的條件下，依預設的聚類數目隨機選擇相應的聚類中心，通過計算各圖像塊到各聚類中心的相似性測度，決定圖像塊的聚類歸屬，隨后將各聚類內部全部圖像塊的均值作為新的聚類中心，再次計算各圖像塊到各聚類中心的相似性測度，進行新一輪的聚類。迭代執行上述過程，直至各聚類中心相對前次迭代的聚類中心無明顯偏移或達到預定迭代數目上限時，方結束迭代并輸出最終聚類結果。其中最為關鍵的2個問題分別是聚類數目的確定和相似度測度的選擇。聚類數目過多會造成聚類頑健性下降，出現聚類碎片效應，對字典學習造成不利的人為影響；但也不宜過少，因為過少會無法準確體現自然圖像中豐富的結構信息。本文以圖像塊灰度值的歐式范數作為相似性測度，并根據聚類分割中常用的貝葉斯信息準則（BIC，Bayesian information criterion）確定聚類數目。

2.2 非參數貝葉斯字典學習建模

設從圖像中采集了N個P×P灰度塊，對其分別做列向量堆棧處理，記作其中M=P×P，i= 1,2,… ,N。此時經過前述聚類操作，此時的數據集是帶有聚類標簽的，這將為后續的字典學習提供重要的結構參考。待學習的字典記作，由K個與xi同維數的原子構成。雖然不需要預置字典原子規模是非參數貝葉斯的一大優勢，但這與K值的選擇并不矛盾，因為非參數貝葉斯字典學習的核心思想是貝葉斯稀疏因子分析，稀疏先驗可以確保信號表示的稀疏性，在K值足夠大的條件下，仍會存在相當數量的原子不參與對信號的表示，很容易確定實際的原子規模。本文算法的核心即基于聚類處理后的數據集和下述非參數貝葉斯模型估計獲得字典D。數據觀測模型為

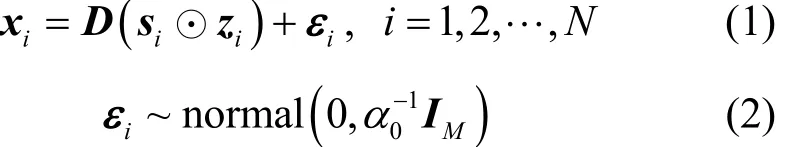
其中，i表示當前圖像塊在采集到的全部圖像塊中的位序；是稀疏表示的權重分量，反映各原子參與表示信號的程度；是稀疏表示的模式分量，反映各原子有無參與對信號的表示；符號⊙是Hadamard乘積，即逐元素對應乘積而不改變向量維數；iε是均值為0的高斯白噪聲，其中0α是觀測噪聲精度，服從Gamma超先驗分布，如式（3）所示。

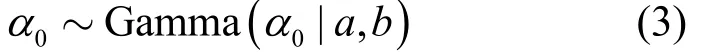
該分布與高斯分布共軛，a和b分別表示形狀參數和尺度參數，為保證噪聲幅值的稀疏性，一般取

式（1）中，當zi的某個元素zik= 0時，sik便不再起作用，因為原子dk并不參與對xi的表示。權重向量si服從如式（4）所示的多元高斯先驗分布。

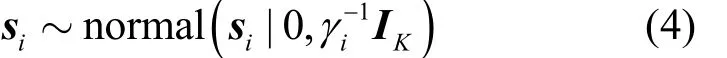
其中

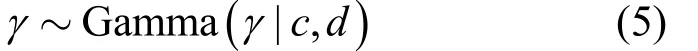
出于防止過擬合的考慮，令權重向量的全部元素使用相同的逆方差γ。類似地，Gamma分布的參數一般取

與基于BPFA的算法相比，本文所提算法將前述聚類過程獲得的全局相似性結構特征引入到稀疏模式向量zi的先驗分布中，如式（6）和式（7）所示。

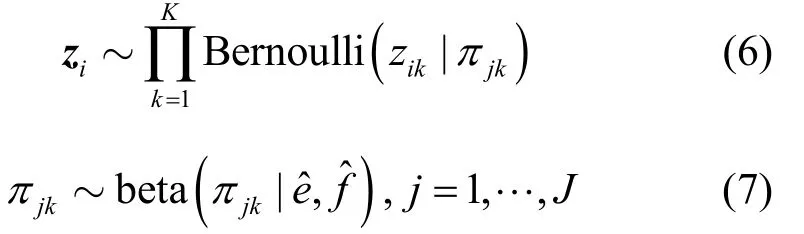
其中，πjk是聚類j中原子dk參與表示數據的概率，J是聚類數目。

假設同一聚類內部的數據對字典原子的使用概率是相同的，允許這些數據不必共用同一支撐集，而是僅在概率意義上具備支撐集的同一性，從而適應了自然信號在空域和時域上普遍存在的支撐集緩變特性。需要指出的是，假設當前數據所屬聚類標簽為j，該聚類內全部數據索引的集合記作則超參數

e?和的取值決定于該聚類中全部數據稀疏模式向量相應元素的毗鄰元素取值。引入符號該符號代表花括號內集合的元素總數；代表集合的元素總數，并分別定義變量1Δ、2Δ和3Δ，如式（8）～式（9）所示和的取值規則如式（11）所示。

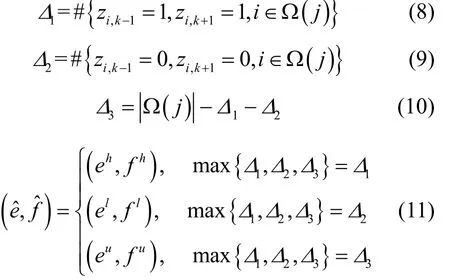
式（8）～式（11）的核心即將馬爾可夫隨機場的思想引入字典學習框架中。當鄰域稀疏模式均為1時，取值為1的概率更大，令有利于生成數值較大的πjk，從而傾向于使zik以較大概率取值為1；當鄰域稀疏模式均為0時，zik取值為0的概率更大，令有利于生成數值較小的πjk，從而傾向于使zik以較大概率取值為0；當鄰域稀疏模式為1和0共存時，zik具備取值的不確定性，此時令可以保證z取值概率的均衡性。

ik

然而，有別于各數據向量具有不同原子使用概率的情形，也有別于所有數據向量共用同一原子使用概率的情形，全局結構相似性聚類后的數據在同一聚類內共用相同的原子使用概率，這是對zik取值的折中處理，也是結構聚類思想的本質要求，為此，需統計聚類內部各數據向量的鄰域稀疏模式，以數量最多的鄰域稀疏模式決定的取值，如式（11）所示。字典原子服從如式（12）所示的高斯先驗分布。

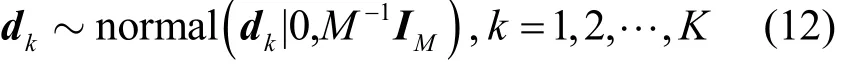
基于上述理論，建立貝葉斯建模的概率圖模型，如圖1所示。

圖1 貝葉斯建模的圖模型

3 貝葉斯推斷

3.1 原子dk的Gibbs采樣

結合式（1）觀測數據模型和式（12）原子先驗分布，可得的dk滿條件分布，如式（13）所示。

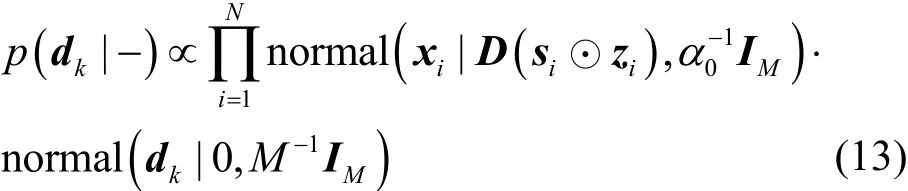
其中

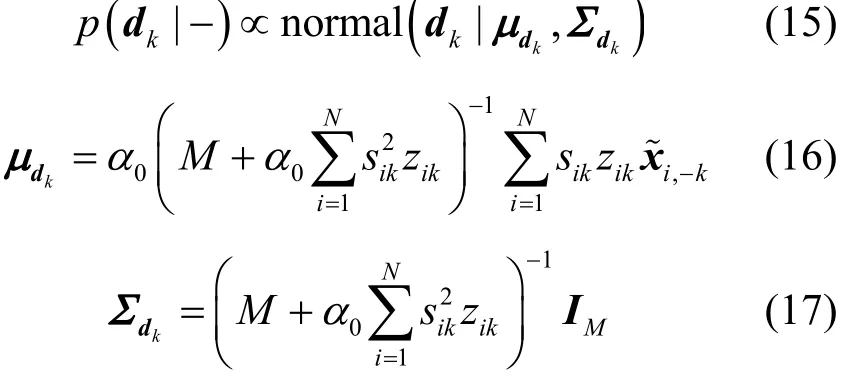
3.2 權重si的Gibbs采樣

結合式（1）觀測數據模型和式（4）權重先驗分布，可得的sik的滿條件分布，如式（18）所示。

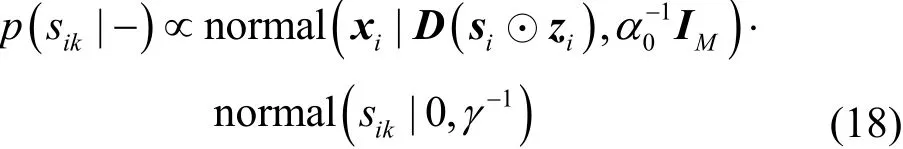
整理可得

3.3 稀疏模式zi的Gibbs采樣

結合式（1）觀測數據模型與式（6）稀疏模式先驗分布，可得zik的滿條件后驗分布，如式（22）所示。

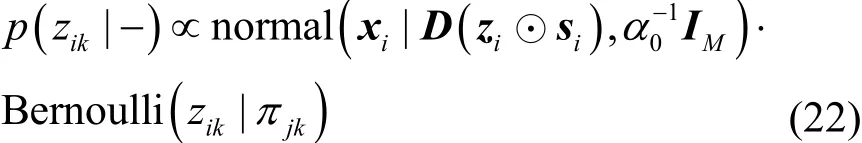
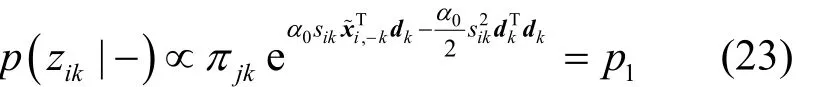
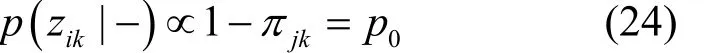
整理可得zik的滿條件分布為Bernoulli分布，即

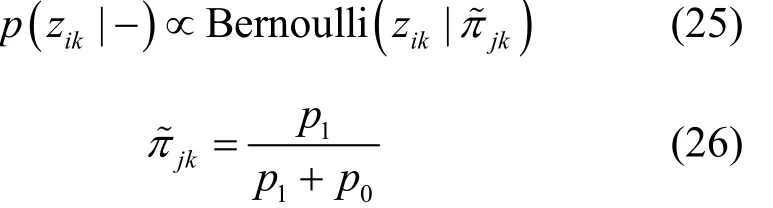
3.4 原子使用概率π的Gibbs采樣

結合式（6）和式（7），可得πjk的滿條件分布，如式（27）所示。

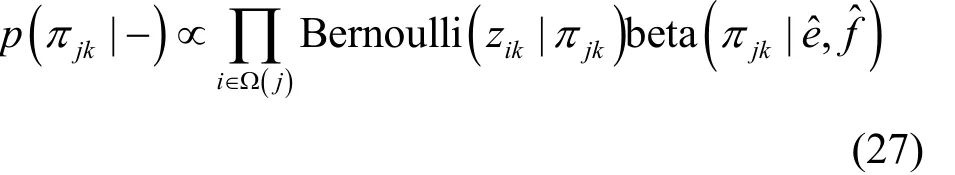
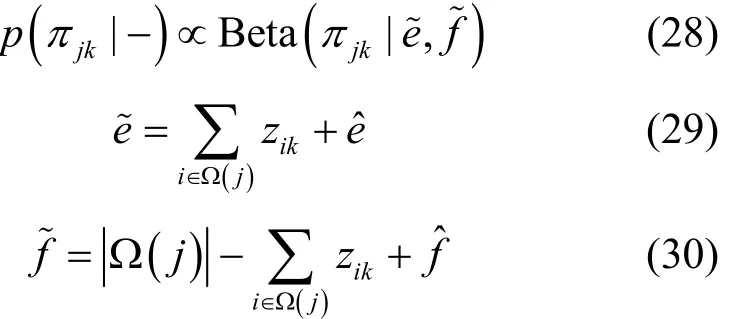
3.5 超參數0α和γ的Gibbs采樣

結合式（1）和式（3），可得超參數0α的滿條件分布，如式（31）所示。

整理可得

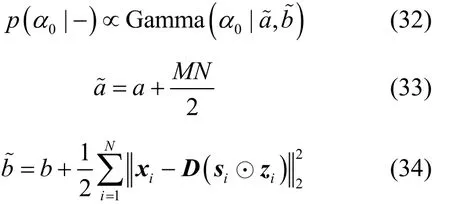
結合式（4）和式（5），可得超參數γ的滿條件分布，如式（35）所示。

整理可得

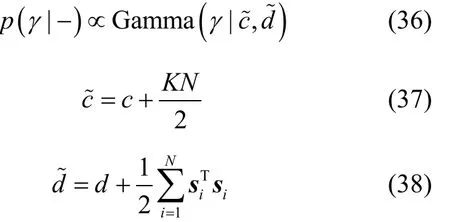
根據式（32）～式（34）可對超參數0α進行Gibbs采樣，根據式（36）～式（38）即可實現對超參數γ的 Gibbs采樣。

迭代執行本節的Gibbs采樣流程，直至達到預定數目的迭代上限，即結束迭代并輸出各隱變量和模型參數的當前采樣值作為推斷結果，完成字典學習，本文與傳統BPFA保持一致，將迭代次數上限設置為 150，為免混淆，本文算法稱為結構相似性beta過程因子分析（SSIM-BPFA，structure similarity-beta process factor analysis）算法，具體流程見算法1。

算法1SSIM-BPFA字典學習算法

輸入圖像塊數據集

初始化超參數當圖像大小超過300×300時令字典原子規模K=512，否則令K=256。

步驟1利用K-均值算法結合傳統的BIC準則對進行聚類預處理，確定聚類數目J，并獲得每個數據點的聚類標簽j，j=1,…,J。

步驟2根據式（1）～式（12）進行貝葉斯概率建模，建立隱變量和模型參數集

步驟3設置迭代總數為150，為當前迭代索引賦值t=1。

步驟4按照式（15）～式（17）對字典原子進行Gibbs采樣。

步驟5按照式（19）～式（21）對權重進行Gibbs采樣。

步驟6按照式（23）～式（26）對稀疏模式進行Gibbs采樣。

步驟7按照式（28）～式（30），并參考式（8）～式（11）對原子使用概率進行Gibbs采樣。

步驟8 分別按照式（32）～式（34）和式（36）～式（38）對超參數0α和γ進行后驗Gibbs采樣。

步驟9 若t=150，則將Θ內各元素的當前采樣值作為估計值；若t≠150，則令t=t+1，并返回步驟4執行迭代。

輸出當前估計的字典，權重和稀疏模式

4 算法分析與數值實驗

本文圍繞圖像去噪和壓縮感知這 2個方面的性能對所提的 SSIM-BPFA算法的有效性展開評估，以圖像處理領域中的Barbara、Lena、Boath、House和Peppers圖像的灰度值作為實驗對象，使用Matlab編程進行數值實驗。

4.1 去噪實驗及性能評估

以分辨率512像素×512像素的圖像Barbara為例，采用滑窗分塊方式將其分割為255 025個具有重疊的8像素×8像素分辨率的圖像塊，并對全部圖像塊的灰度值進行列堆棧處理，構成算法執行所使用的數據集。按照SSIM-BPFA算法的流程進行字典學習，并將初始字典原子數目設置為512 個，訓練所得字典如圖2所示。

圖2 SSIM-BPFA算法訓練所得圖像字典

設噪聲標準差σ=25，采用SSIM-BPFA算法對Barbara進行去噪處理，結果如圖3所示。可見相比于圖 3（b）所示的含噪圖像，圖 3（c）所示的去噪圖像的峰值信噪比（SNR，signal noise ratio）顯著提高，圖像視覺效果也得到了明顯的改善，而且運行時間較BPFA算法并未有明顯的增加。

圖3 SSIM-BPFA算法去噪實驗結果

為進一步驗證 SSIM-BPFA算法的性能，除Barbara外又增加了Lena、Boat、House、Peppers等作為實驗圖像，并引入MOD、K-SVD、傳統的離散余弦傅里葉變換（DCT，discrete cosine transformation）等傳統的字典學習算法與本文的SSIM-BPFA算法進行比較。實驗過程中，分別采用噪聲的標準差為5、10、15和25這4種參數進行實驗。實驗結果顯示，噪聲標準差等于5、10、15時7種算法的去噪結果與表1相似，只是在噪聲標準差較大時對比更為顯著。因此，本文以為例，對比了SSIM-BPFA和其他6種算法對實驗圖像去噪處理后的峰值信噪比結果，如表1所示，表中的實驗結果是進行50次實驗后，實驗結果的平均值。

由表1可知，SSIM-BPFA的去噪峰值信噪比明顯高于其他 6種算法，其中 BPFA、DP-BPFA和dHBP這3種算法的去噪性能相近，這與Zhou的研究結論是一致的[7]。

4.2 壓縮感知實驗及性能評估

利用前述去噪過程中7種不同算法分別學習獲得的字典，結合相應的壓縮感知算法，對經觀測矩陣降維投影后的圖像數據進行重構。Zhou[7]的研究已經證實了BPFA算法相對其他字典學習算法在壓縮感知應用中的優勢，所以限于篇幅，本節實驗著重對SSIM-BPFA算法所得字典與BPFA、DP-BPFA和dHBP這3種算法所得字典進行壓縮感知性能對比。為便于比較分析，仍以Barbara作為實驗對象，出于克服塊結構效應的重構需求，實驗數據的生成方式仍采用4.1節的滑窗法。由于前述字典學習過程中，圖像塊在字典表示下的稀疏度普遍不超過4，故出于提高重構成功概率的目的，本節實驗選擇的投影觀測矩陣行數以8為下限，設置了行數分別為8、10、12、14、16、18等共6種觀測數目作為實驗條件，所用投影觀測矩陣的元素獨立同分布地采樣自標準正態分布。

表1 不同字典學習算法的圖像去噪峰值信噪比

圖4所示即觀測數目為8時，壓縮感知經典的正交匹配追蹤（OMP，orthogonal matching pursuit）算法分別在 SSIM-BPFA算法、BPFA算法、DP-BPFA算法和dHBP算法所得字典下對Barbara的重構結果及相應的峰值信噪比。由圖可見，圖4（d）在視覺效果和峰值信噪比方面均顯著優于圖 4（a）～圖4（c）。在Lena等其他4幅實驗圖像的壓縮感知實驗中，SSIM-BPFA算法所得字典也體現出了同樣的優越性。

圖4 Barbara重構結果及峰值信噪比

為了進一步驗證不同投影觀測數目條件下SSIM-BPFA所得字典的壓縮感知性能，圖5給出了觀測數目分別為8、10、12、14、16、18等共6種條件下，在SSIM-BPFA算法、dHBP算法、DP-BPFA算法、BPFA算法和OMP算法所得字典表示下分別通過OMP算法對Barbara的重構相對誤差，數據為50次實驗結果的平均值。

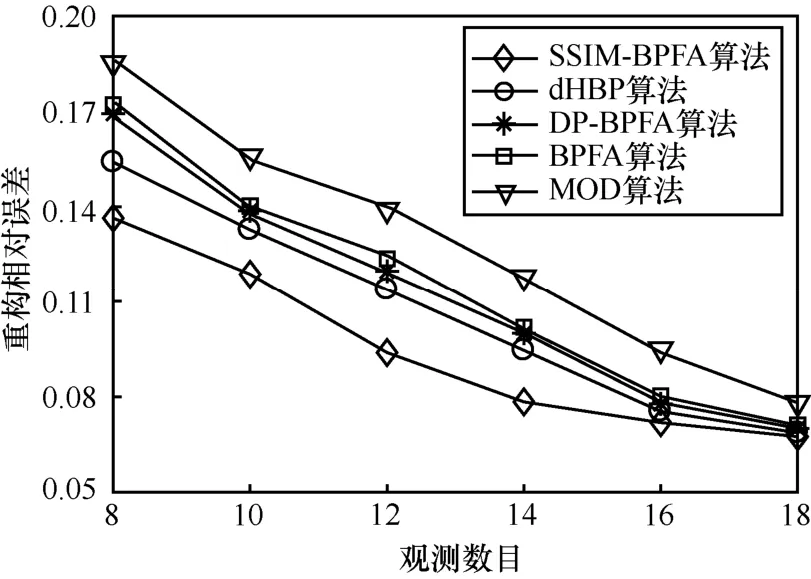
從圖5可以看出，隨著觀測數目的增加，不同算法字典下的重構相對誤差均呈下降趨勢，但總體重構相對誤差由低到高分別是 SSIM-BPFA算法、dHBP算法、DP-BPFA算法、BPFA算法和MOD算法所得字典，其中，前四種算法重構相對誤差均顯著低于 MOD算法字典的重構相對誤差，且SSIM-BPFA字典的重構相對誤差顯著低于其他字典的重構相對誤差，這從另一個側面表明SSIM-BPFA算法學習所得字典在壓縮感知中的應用性能優于其他幾種算法所得字典。其原因在于SSIM-BPFA算法基于全局結構相似性對圖像進行了聚類處理，并引入了稀疏表示的塊結構特性，使得字典對圖像結構特征的表示性能得以改善，圖像表示的稀疏度更小，從而提高了低觀測數目條件下的重構成功率。盡管Gibbs采樣推斷方法的理論收斂性不易證明，但關于該推斷方法收斂效果的可靠性和有效性均已在前人研究成果[9-12]中得到了實驗驗證。

5 結束語

本文提出一種基于結構相似性的非參數貝葉斯字典學習算法，將馬爾可夫隨機場思想引入到圖像稀疏表示的塊結構建模中，使字典具備了傳統結構字典稀疏表示的塊結構特性。實驗表明，該算法所得字典的去噪性能和壓縮感知性能優于BPFA算法、DP-BPFA算法和dHBP算法這3種非參數貝葉斯算法字典。本文以后將在兩方面進行下一步研究：1）Gibbs采樣推斷計算量相對較大，這是BPFA算法同樣面臨的問題，且采樣推斷收斂性能的可靠性和有效性不易于理論證明，后續將研究效率更高的推斷算法，并著重加強理論證明；2）圖像結構相似性聚類過程采用K-means算法執行，雖簡單易行復雜度低，但需要進行聚類數目的驗證性優化，限制了算法的自適應性和頑健性，后續應著重提升無監督聚類的自適應性，以期在可觀的復雜度之外，進一步改善字典的應用性能。