廣義變分不等式的一種新解法

張冬楊, 葛鑫磊

(渤海大學 數理學院, 遼寧 錦州 121000)

變分不等式理論是當今非線性分析的重要組成部分.它在力學、微分方程等方面有著非常廣泛的應用.

自20世紀60年代以來,Lious、Brower等人提出和創立變分不等式的基本理論以來,經過許多數學工作者的努力,變分不等式的研究已經取得了重要的進展,并且日臻完善.到目前為止,變分不等式的理論,已成為一門內容十分豐富的邊緣學科并有著廣泛的應用前景.

Hilbert和Banach空間中的距離投影算子在眾多數學領域中都有比較廣泛的應用,例如泛函分析、數值分析、優化和逼近論、最優控制、非線性隨機規劃等.

雖然Hilbert空間中的距離投影算子和Banach空間中的距離投影算子定義相似,但是仍然存在著本質上的區別,在Hilbert空間中的距離投影算子是單調的,非擴張.而Banach空間中的投影算子卻沒有這樣的性質.為了克服這樣的限制,1996年Alber[1]在一致凸且一致光滑的Banach空間中引入了廣義投影算子φK:B*→K和φK:B→K,它們是從Hilbert空間到一致凸且一致光滑的Banach空間.這種算子繼承了Hilbert空間距離投影算子的很多性質,在2001年,Alber在Banach空間中借用廣義投影算子來計算變分不等式的近似解.

隨著距離投影算子研究的不斷深入,應用距離投影算子求解廣義變分不等式取得了較多的研究成果.

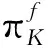
在提出求解變分不等式的新方法之前,我們需要一些預備知識.

1 預備知識

令X是Banach空間,X*為X的對偶空間,K為X的非空閉凸子集,f:K?X→R∪{+∞}是真凸下半連續函數.

Banach空間X上的對偶映射J:X→X*可以定義為

對偶映射J具有下述性質[1]:

(1)X是自反的當且僅當J是滿射;

(2)X是嚴格凸的當且僅當J是單射;

(3)X是光滑的當且僅當J是單值映射;

(4) 如果X是光滑的Banach空間,那么J:X→X*是弱*連續的;

(5) 如果X是自反嚴格凸且光滑的Banach空間,那么J*:X*→X是X*中的對偶映射且J-1=J*,J*J=I.

令X是一致凸且光滑的Banach空間,V2:X×X→R可以定義為V2(x,y)=V(Jx,y),其中任意的x,y∈K.

對任意給定的ρ>0,令G:X*×K→R∪{+∞},定義

G(φ,x)=‖φ‖2-2〈φ,x〉+‖x‖2+ρf(x)

G函數的性質[2]如下:

(1) (‖φ‖-‖x‖)2+ρf(x)≤G(φ,x)≤(‖φ‖+‖x‖)2+ρf(x);

(2) 對φ而言,如果x是固定的,那么G(φ,x)是凸的,連續的;

(3) 對x而言,如果φ是固定的,那么G(φ,x)是凸的,下半連續的.

在已有G函數的基礎上,Wu和Huang[2]在一致凸且一致光滑的Banach空間中定義了廣義f-投影算子,即:

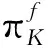
〈u,y-x〉+ρf(y)-ρf(x)≥0,?y∈K.

(1)

其中,T:K→X*是集值變換.

在文章中,還需要如下引理:

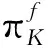
引理2[5]如果對任意x∈K,ρ>0都有f(x)>0,那么

引理3[5]如果是任意給定的實數r>0,那么X是一致凸的Banach空間當且僅當存在嚴格遞增的凸函數g:R+→R+,且g(0)=0,使得

其中?x,y∈Br,λ∈[0,1].

引理4[6]令X是一致凸且光滑的Banach空間且{yn}、{zn}是X中的兩個序列,如果V2(zn-yn)→0,且{yn}或{zn}是有界的,那么zn→yn→0.

2 主要結果

定理令X是一致凸且光滑的Banach空間且其對偶空間為X*,K是X的非空閉凸子集且0∈K,令f:K→R是真凸下半連續的,T:K→X*是上半連續且閉的.假設存在β>0使得任意x∈K,u∈Tx都有

且J-βT:K→X*是緊的.令Ω是變分不等式GVI(K,T,f)的解集.假設

(2)

令x0∈X,且{xn}是由下列迭代結構產生的:

其中{αn}滿足下列條件:

(1) 0≤αn≤1;

那么,廣義變分不等式GVI(K,T,f)存在近似解x*∈K,且存在{xni}?{xn},使得當i→∞時,xni→x*.

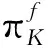
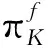
由引理3和式(2)可以得到

另一方面,由G函數的定義及引理2可得

因為X是一致凸的,那么‖·‖是嚴格凸的,也就是說

結合式(4)和式(5),有‖xn+1‖≤‖xn‖.

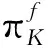
由引理3可知,存在連續且嚴格遞增的凸函數g:R+→R+且g(0)=0,那么

由式(2)可知

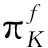
由g函數的非負性,可得

G(Jxn+1,x*)≤G(Jxn,x*),

即{G(Jxn,x*)}是遞減的,也就是{V2(xn,x*)}也是遞減的.由于xni→x*和J的弱*連續性,可得

即V2(xni,x*)→0(i→∞),xni→x*.