矮塔斜拉橋斜拉索無索區(qū)長度研究

吳清偉

(浙江省建設(shè)工程質(zhì)量檢驗(yàn)站有限公司,浙江 杭州 310012)

1 概 述

矮塔斜拉橋[1]的上部結(jié)構(gòu)是由主梁、主塔和斜拉索有機(jī)組合在一起的共同受力體系,斜拉索是柔性線材,它依附錨固在主梁和主塔上,布置在主梁與主塔之間,與主梁、主塔共同發(fā)揮作用一起承擔(dān)結(jié)構(gòu)自重和外荷載；斜拉索[2-3]是矮塔斜拉橋的主要承重構(gòu)件之一,分擔(dān)著結(jié)構(gòu)承受的外荷載,斜拉索的布置合理與否對矮塔斜拉橋的結(jié)構(gòu)性能有著很大的影響。因此，很有必要對矮塔斜拉橋的斜拉索布置進(jìn)行研究。斜拉索的布置包括無索區(qū)長度的設(shè)計(jì)和斜拉索間距設(shè)計(jì),前者主要包括塔根無索區(qū)長度、跨中無索區(qū)長度和邊跨無索區(qū)長度,后者則包含主梁上的斜拉索間距和主塔上的斜拉索間距。本文主要結(jié)合矮塔斜拉橋的工程實(shí)例對無索區(qū)長度參數(shù)進(jìn)行了對比分析,探討矮塔斜拉橋的斜拉索布置規(guī)律,以便對依托工程的結(jié)構(gòu)設(shè)計(jì)有所指導(dǎo)。

斜拉索的布置主要涉及到斜拉索的布設(shè)位置和布置方式,其布設(shè)位置主要包括主梁上的布置和主塔上的布置,主梁上的布索區(qū)位置主要由無索區(qū)長度來控制。在布索區(qū)位置確定以后,根據(jù)不同的布索方式,斜拉索的布置又可以分為扇形、豎琴形、輻射形。在這方面,本文主要探討主梁上的無索區(qū)長度對矮塔斜拉橋結(jié)構(gòu)性能的影響。

2 依托工程及計(jì)算模型

2.1 依托工程

本文以一座矮塔斜拉橋?yàn)楣こ瘫尘癧4],該橋平面位于平曲線上,平曲線半徑R=850 m,跨徑布置為：75 m+125 m+75 m；該橋是一座雙塔單索面預(yù)應(yīng)力混凝土矮塔斜拉橋,采用塔梁固結(jié)、塔墩分離、梁底設(shè)支座的結(jié)構(gòu)體系,見圖1。

主梁采用單箱三室大懸臂變截面PC連續(xù)箱梁,支點(diǎn)梁高4.2 m,跨中梁高2.3 m,箱梁頂寬28 m,懸臂板長5 m。邊箱凈寬6.776 m,中室凈寬2.6 m,斜拉索錨固點(diǎn)布置在箱梁中室內(nèi)橫隔板處,間距4 m。見圖2。

圖1 橋型布置示意圖(一半上部結(jié)構(gòu))

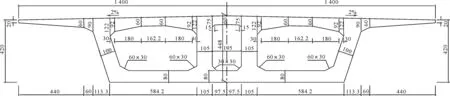
圖2 箱梁支座處結(jié)構(gòu)尺寸圖(單位：cm)

主塔采用鋼筋混凝土獨(dú)柱實(shí)心矩形截面,塔高24.5 m,順橋向長3 m,橫橋向?qū)? m,布置在中央分隔帶上,并與主梁固結(jié)。塔身上部設(shè)鞍座,以便斜拉索通過。鞍座采用分絲管結(jié)構(gòu)形式,分絲管預(yù)埋于主塔中,在施工中,斜拉索穿過對應(yīng)的每一個(gè)分絲管。

斜拉索為單索面,雙排布置在中央分隔帶上,每個(gè)塔上設(shè)9對18根斜拉索,全橋共36根,采用環(huán)氧鋼絞線；斜拉索分3種,從塔根往兩側(cè),每3根一組,分別為小索(31Φ15.24)、中索(34Φ15.24)、大索(37Φ15.24)。

2.2 計(jì)算模型

采用橋梁結(jié)構(gòu)分析軟件Midas Civil對該矮塔斜拉橋進(jìn)行有限元仿真分析,結(jié)構(gòu)計(jì)算采用空間梁單元模型,以主梁軸線為基準(zhǔn)劃分結(jié)構(gòu)離散圖,主塔和主梁為空間梁單元,斜拉橋索為平面桁架單元；主梁懸臂澆注區(qū)段按每個(gè)施工節(jié)段并兼顧主梁斜拉索錨固位置劃分單元,全橋模型共有335個(gè)節(jié)點(diǎn),劃分334個(gè)單元,其中主梁劃分為274個(gè)單元,主塔劃分為24個(gè)單元,斜拉索劃分為36個(gè)單元。有限元分析模型見圖3。

計(jì)算荷載如下：

①恒載：分為一期恒載和二期恒載。一期恒載包括主要構(gòu)件材料重量。混凝土容重取26 kN/ m3,主要構(gòu)件按實(shí)際截面計(jì)取重量,主梁橫隔板以集中力計(jì)入。二期恒載為橋面防撞護(hù)欄、分隔帶護(hù)欄、泄水管及橋面鋪裝,二期恒載取112.6 kN/m。

②活載：采用公路-Ⅰ級荷載,主梁為四車道加載,橫向折減系數(shù)為0.67,汽車荷載偏載增大系數(shù)取1.15。

③荷載組合：根據(jù)《公路鋼筋混凝土及預(yù)應(yīng)力混凝土橋涵設(shè)計(jì)規(guī)范(JTG D62—2004)》荷載組合分為標(biāo)準(zhǔn)組合,短期效應(yīng)組合,長期效應(yīng)組合和基本組合,各組合荷載值及系數(shù)采用規(guī)范規(guī)定。本文計(jì)算的荷載組合選取在各種組合下最不利內(nèi)力包絡(luò)。

圖3 計(jì)算模型圖

3 無索區(qū)長度的影響分析

本文矮塔斜拉橋是相對于橋梁中點(diǎn)對稱布置的,且斜拉索的布置是每個(gè)主塔對稱,那么邊跨無索區(qū)長度與塔根無索區(qū)長度和跨中無索區(qū)長度之間就存在一定的換算關(guān)系,因此分析時(shí)不使用邊跨無索區(qū)長度這個(gè)參數(shù),只考慮塔根無索區(qū)長度和跨中無索區(qū)長度這兩個(gè)獨(dú)立變量的變化對矮塔斜拉橋受力和變形的影響。在分析塔根和跨中無索區(qū)長度變化對矮塔斜拉橋的影響時(shí),保持布索區(qū)域長度不變,只變化塔根無索區(qū)長度和跨中無索區(qū)長度,也可以用塔根與跨中的無索區(qū)長度比值(LT/LZ)這個(gè)參數(shù)為變量,進(jìn)行有限元模擬對比計(jì)算,來分析塔根與跨中的無索區(qū)長度變化對矮塔斜拉橋的影響。

根據(jù)該橋的原有設(shè)計(jì)方案,保持布索區(qū)域長度LC=32 m不變,對塔根與跨中的無索區(qū)長度進(jìn)行變化,分別建立有限元模型進(jìn)行對比計(jì)算分析,具體選取以下五種計(jì)算模式：

模式一：塔根無索區(qū)長度LT=15.5 m,跨中無索區(qū)長度LZ=30 m,結(jié)構(gòu)形式及其余結(jié)構(gòu)參數(shù)不變；

模式二：塔根無索區(qū)長度LT=18.5 m,跨中無索區(qū)長度LZ=24 m,結(jié)構(gòu)形式及其余結(jié)構(gòu)參數(shù)不變；

模式三：塔根無索區(qū)長度LT=21.5 m,跨中無索區(qū)長度LZ=18 m,結(jié)構(gòu)形式及其余結(jié)構(gòu)參數(shù)不變；

模式四：塔根無索區(qū)長度LT=24.5 m,跨中無索區(qū)長度LZ=12 m,結(jié)構(gòu)形式及其余結(jié)構(gòu)參數(shù)不變；

模式五：塔根無索區(qū)長度LT=27.5 m,跨中無索區(qū)長度LZ=6 m,結(jié)構(gòu)形式及其余結(jié)構(gòu)參數(shù)不變。

3.1 塔根與跨中的無索區(qū)長度比值對主梁的影響

通過對這五種計(jì)算模式進(jìn)行有限元模擬計(jì)算分析,可得到塔根與跨中的無索區(qū)長度比值變化對主梁的受力和變形的影響數(shù)據(jù),見表1、表2。

由有限元模型的對比計(jì)算分析數(shù)據(jù)可知,當(dāng)布索區(qū)域長度不變時(shí),可以得到塔根與跨中的無索區(qū)長度比值變化對曲線主梁的影響有以下幾點(diǎn)規(guī)律：

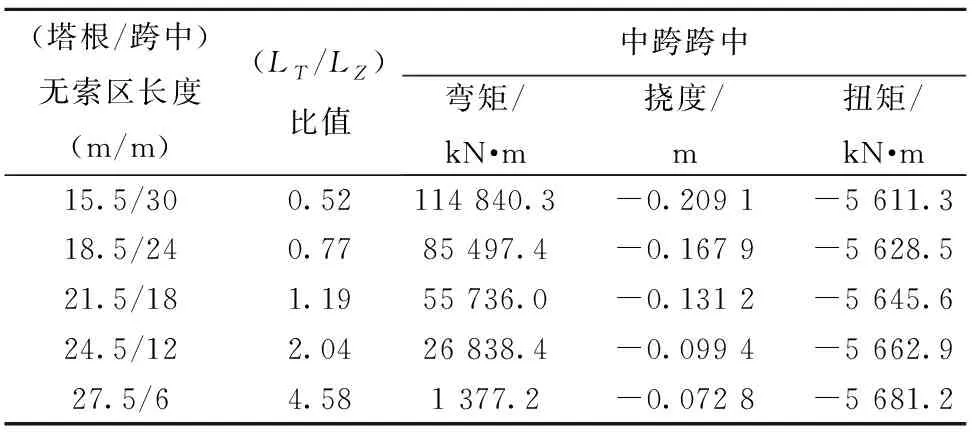
表1 塔根與跨中的無索區(qū)長度比值對中跨跨中的影響數(shù)據(jù)

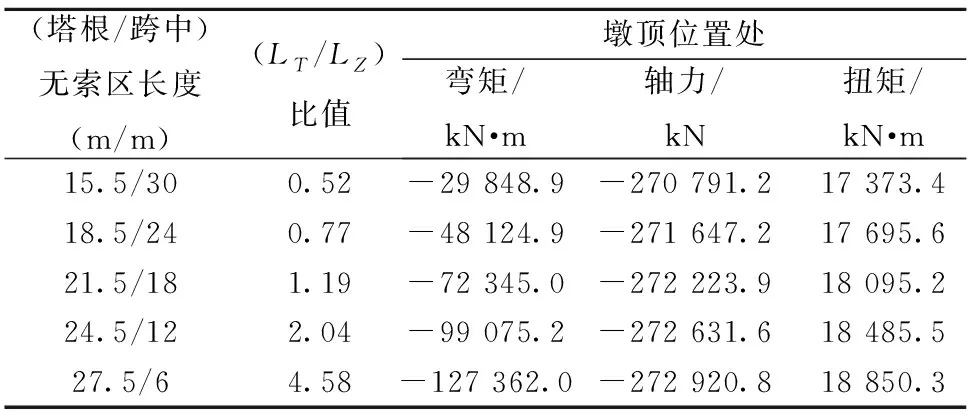
表2 塔根與跨中的無索區(qū)長度比值對墩頂處影響數(shù)據(jù)

1)隨著塔根與跨中的無索區(qū)長度比值不斷增加,中跨跨中彎矩逐漸減小,呈線性變化趨勢；塔根無索區(qū)長度每增加3 m(跨中無索區(qū)長度對應(yīng)減少6 m)時(shí),跨中彎矩減少約30 000 kN·m。

2)隨著塔根與跨中的無索區(qū)長度比值不斷增加,中跨跨中撓度逐漸減小,減幅速率稍有減緩；塔根無索區(qū)長度每增加3 m(跨中無索區(qū)長度對應(yīng)減少6 m)時(shí),跨中撓度減少20%左右。

3)隨著塔根與跨中的無索區(qū)長度比值不斷增加,中跨的跨中扭矩逐漸增大,呈線性變化趨勢；塔根無索區(qū)長度每增加3 m(跨中無索區(qū)長度對應(yīng)減少6 m)時(shí),跨中扭矩增大約3‰,受塔根與跨中的無索區(qū)長度比值變化的影響不大。

4)隨著塔根與跨中的無索區(qū)長度比值不斷增加,墩頂處主梁彎矩逐漸增大,增幅速率也逐漸加大；塔根無索區(qū)長度每增加3 m(跨中無索區(qū)長度對應(yīng)減少6 m)時(shí),主梁彎矩增大18 000～28 000 kN·m,增加量逐漸加大。

5)隨著塔根與跨中的無索區(qū)長度比值不斷增加,墩頂處的主梁軸力逐漸增大,增幅速率逐漸放緩；塔根無索區(qū)長度每增加3 m(跨中無索區(qū)長度對應(yīng)減少6 m)時(shí),主梁軸力增加1‰～3‰,增加量逐漸減小,受塔根與跨中的無索區(qū)長度比值變化的影響不大。

6)隨著塔根與跨中的無索區(qū)長度比值不斷增加,墩頂處主梁扭矩逐漸增大,基本呈線性變化趨勢；塔根無索區(qū)長度每增加3 m(跨中無索區(qū)長度對應(yīng)減少6 m)時(shí),主梁扭矩增大2%左右。

3.2 塔根與跨中的無索區(qū)長度比值對主塔和斜拉索的影響

通過對這五種計(jì)算模式進(jìn)行有限元模擬計(jì)算分析,可得到塔根與跨中的無索區(qū)長度比值變化對主塔和斜拉索的影響數(shù)據(jù),見表3、表4；主塔的分析目標(biāo)包括塔根彎矩和塔頂位移,并考慮了曲線橋的順橋向與橫橋向的對比,斜拉索的分析目標(biāo)選為索力和拉索應(yīng)力,可以反映索力和拉索應(yīng)力的總體變化趨勢,同時(shí)也可以獲得索力和拉索應(yīng)力的最大值與最小值之間的變化趨勢規(guī)律。

表3 塔根與跨中的無索區(qū)長度比值對主塔的影響數(shù)據(jù)

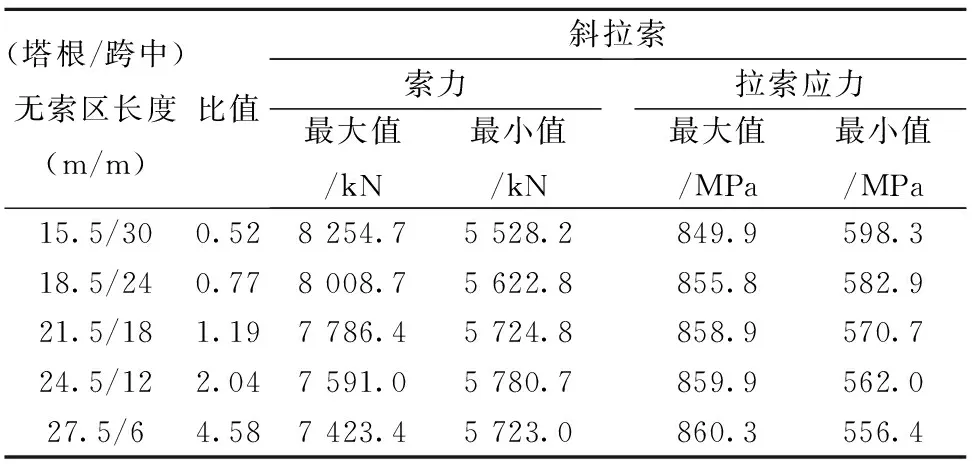
表4 塔根與跨中的無索區(qū)長度比值對斜拉索的影響數(shù)據(jù)

根據(jù)有限元模型的對比計(jì)算分析數(shù)據(jù)得知,當(dāng)布索區(qū)域長度不變時(shí),可以得到塔根與跨中的無索區(qū)長度比值變化對矮塔斜拉橋主塔和斜拉索的影響有以下幾點(diǎn)規(guī)律：

1)隨著塔根與跨中的無索區(qū)長度比值不斷增加,塔根順橋向彎矩和塔根橫橋向彎矩變化趨勢不同,塔根橫橋向彎矩隨比值的增加而逐漸增大,塔根順橋向彎矩隨比值增加的變化則不是很規(guī)律；塔根無索區(qū)長度每增加3 m(跨中無索區(qū)長度對應(yīng)減少6 m)時(shí),塔根橫橋向彎矩增大8%左右,而塔根順橋向彎矩則隨比值的增加先增大,然后最大彎矩方向發(fā)生變化,之后逐漸減小,出現(xiàn)一個(gè)極大值拐點(diǎn)；塔根橫橋向彎矩是塔根順橋向彎矩的4～5倍。

2)隨著塔根與跨中的無索區(qū)長度比值不斷增加,塔頂X軸方向位移和塔頂Y軸方向位移都基本呈線性變化趨勢,但是趨勢方向不同,一個(gè)逐漸減小,一個(gè)逐漸增大；塔根無索區(qū)長度每增加3 m(跨中無索區(qū)長度對應(yīng)減少6 m)時(shí),塔頂X軸方向位移減小20%左右,而塔頂Y軸方向位移則增加8%左右,兩者之間的差值越來越大。

3)隨著塔根與跨中的無索區(qū)長度比值不斷增加,最大索力逐漸減小,呈線性變化趨勢；塔根無索區(qū)長度每增加3 m(跨中無索區(qū)長度對應(yīng)減少6 m)時(shí),最大索力減小3%左右,而最小索力受塔根與跨中的無索區(qū)長度比值變化的影響較小,最小索力隨比值增加的變化趨勢是先增大后減小,出現(xiàn)一個(gè)極大值拐點(diǎn)；最大索力是最小索力的1.3～1.5倍。

4)隨著塔根與跨中的無索區(qū)長度比值不斷增加,最大拉索應(yīng)力和最小拉索應(yīng)力變化趨勢不同,最大拉索應(yīng)力逐漸增大,最小拉索應(yīng)力逐漸減小；塔根無索區(qū)長度每增加3 m(跨中無索區(qū)長度對應(yīng)減少6 m)時(shí),最大拉索應(yīng)力增加不足1%,最小拉索應(yīng)力減小2%左右,最大和最小拉索應(yīng)力受塔根與跨中的無索區(qū)長度比值變化的影響較小；最大拉索應(yīng)力是最小拉索應(yīng)力的1.4～1.6倍。

4 結(jié) 語

塔根與跨中的無索區(qū)長度比值對結(jié)構(gòu)性能的影響規(guī)律：塔根與跨中的無索區(qū)長度比值變化對矮塔斜拉橋主梁的影響趨勢比較明顯,隨著塔根與跨中的無索區(qū)長度比值不斷增加,中跨的跨中彎矩和跨中撓度逐漸減小,中跨跨中扭矩逐漸增大,墩頂處的主梁彎矩、主梁軸力和主梁扭矩逐漸增大；塔根橫橋向彎矩隨無索區(qū)長度比值的增加逐漸增大,塔根順橋向彎矩先增大后減小；塔頂位移受塔根與跨中的無索區(qū)長度比值的影響很大,塔頂順橋向位移逐漸減小,塔頂橫橋向位移逐漸增大；索力和拉索應(yīng)力的變化范圍受塔根與跨中的無索區(qū)長度比值的影響很小。