基于編碼一解碼對稱神經網絡的高分辨率圖像重構機理研究

熊銳 張雷洪 蔣周杰 王建強 覃榜道 賴純莉

摘要：針對目前許多圖像重構算法存在重構出來的圖像不清晰、分辨率低等問題，提出了一種基于編碼一解碼對稱神經網絡的高分辨率圖像重構算法。首先將圖像進行壓縮獲取低分辨率圖像，然后將低分辨率圖像作為輸入圖像經過編碼一解碼對稱神經網絡，并利用其中的卷積神經網絡進行編碼得到特征圖像，最后再利用反卷積神經網絡進行解碼實現圖像的細節恢復。實驗結果表明，經過基于編碼一解碼對稱神經網絡重構出來的圖像比之前的低分辨率圖像更加清晰，圖像的分辨率得到了提高。

關鍵詞：卷積神經;反卷積神經;編碼;解碼;重構

中圖分類號：TP311.1 文獻標志碼：A

引言

隨著越來越多的智能服務出現，人類將進入一個新的智能時代，而深度學習無疑是這股智能浪潮的前沿科技。深度學習是通過提取和組合低層特征形成高層特征來表示其屬性類別，便于數據的表示。目前常用的深度學習有三種，分別是卷積神經網絡、受限制波茲曼機以及自編碼神經網絡。1986年，Rumelhart等提出的反向傳播算法解決了多層神經網絡的訓練問題。1990年，Cun等首次提出了卷積神經網絡（convolut-ional neural network，CNN），其特點在于卷積層采用局部連接和權值共享的方式進行連接，從而大大降低了需要訓練的參數數量，通過降采樣層來降低維度，使網絡具有更高的魯棒性，同時能夠有效地防止擬合。卷積神經網絡作為深度學習的網絡模型之一，是專門做圖像信息處理的深度神經網，應用于大多數的計算機視覺領域，目前正處于陜速發展階段。因此，本文將卷積神經網絡與反卷積神經網絡相結合，提出了一種基于編碼一解碼對稱神經網絡的高分辨率圖像重構算法。此算法的特點在于：先將壓縮圖像作為輸入圖像，經過編碼階段，利用卷積神經網絡來獲得特征圖像;然后再經過解碼階段，利用反卷積神經網絡來實現圖像細節的恢復，以期取得更好的圖像重構效果。

1圖像處理的神經網絡

1.1卷積神經網絡

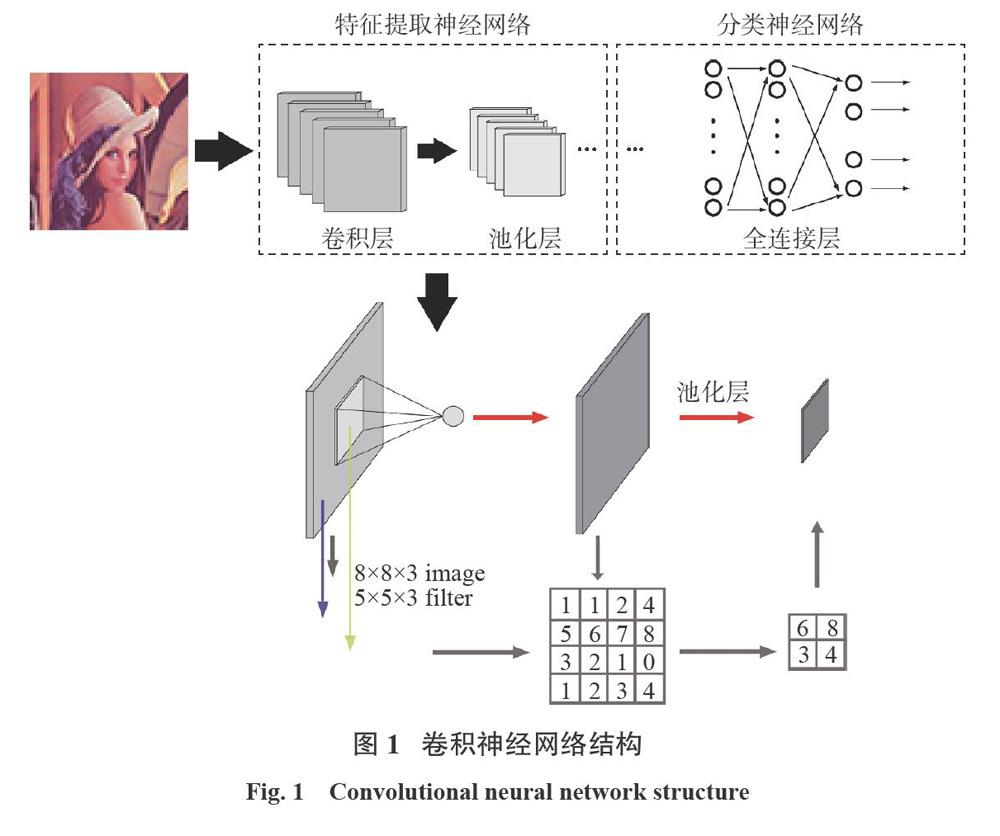
圖1為卷積神經網絡結構，該結構是由多個卷積層與池化層相互交替組合而成。卷積神經網絡與其他神經網絡的不同之處在于采用了轉換圖像的過濾器，稱之為“卷積過濾器”。使用卷積過濾器可使經卷積層后生成的特征圖像突出了原始圖像的獨特特征。在卷積層中，每層設置了多少個卷積過濾器，相應地將會產生多少個特征映射，最后這些特征映射經過激活函數就可以得到特征圖像。

由于神經網絡輸出端輸出的實際值與理論值會存在一定的誤差，所以需要通過一個算法來降低輸出誤差，以此達到優化整個神經網絡的目的。因此利用反向傳播算法對神經網絡結構中的各個權重以及參數進行優化。

1.2反卷積神經網絡

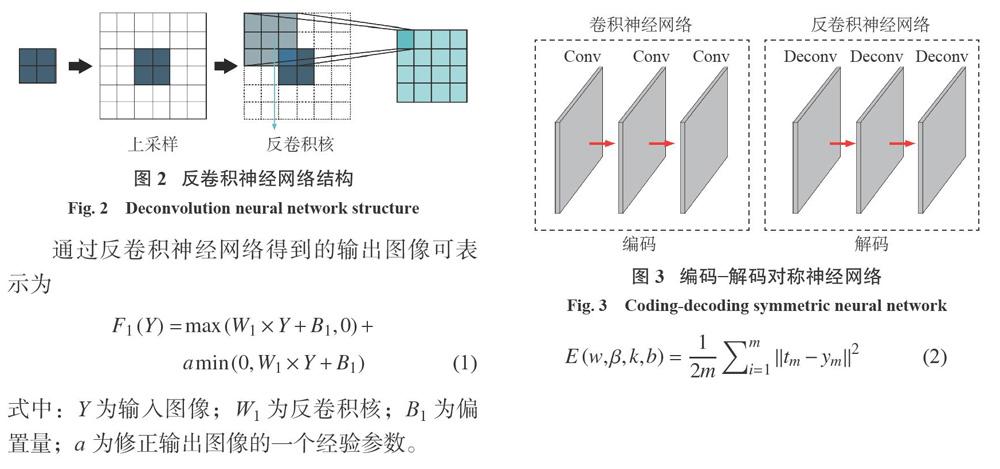
反卷積神經網絡是在卷積神經網絡的基礎上對其進行改進得到的。圖2為反卷積神經網絡結構，其結構與卷積神經網絡不同之處在于去掉了卷積神經網絡中最后的全連接層，在網絡中加入反卷積層。為了得到比輸入圖像尺寸更大的輸出圖像，對輸入圖像進行上采樣操作來擴大圖片尺寸，同時通過使用反卷積過濾器對圖像進行卷積以此來填充圖像的內容，使得圖像內容變得豐富。這樣一個由反卷積層、上采樣層組成的層次化的反卷積神經網絡結構有助于提取圖像的細節特征。

為了得到更高的神經網絡重構圖像分辨率，本文將卷積神經網絡與反卷積神經網絡相結合，采用一種基于編碼一解碼對稱神經網絡的圖像高分辨率重構方法。

2基于編碼一解碼對稱神經網絡的圖像重構

在典型的卷積神經網絡中，網絡初始端通常是多個卷積層和池化層的交替組合，在靠近輸出層的最后幾層網絡是全連接網絡。但是在卷積層提取圖像特征時，會丟失一些細節信息，如邊緣、紋理等，隨著網絡層數的加深，細節信息的丟失會逐漸增加，這不利于圖像超分辨率重構及恢復。因此，為了避免過多的細節丟失，本文刪除了池化層，并在卷積神經網絡后增加了一個反卷積神經網絡，卷積神經網絡充當編碼器用以得到特征圖像，反卷積神經網絡充當解碼器用以恢復原始圖像。

圖3為編碼一解碼對稱神經網絡結構示意圖，主要有兩部分構成。第一部分（編碼）為基于卷積神經網絡的特征提取，給定原始圖像和隨機初始化卷積過濾器矩陣，利用卷積神經網絡直接對原始圖像進行操作生成特征映射，卷積過濾器矩陣的值是在訓練過程中經不斷優化確定的。第二部分（解碼）為基于反卷積神經網絡的圖像細節的恢復，將經卷積神經網絡得到的特征圖像作為反卷積神經網絡的輸入，反卷積核是經卷積過濾器矩陣變換得到，在一定程度上可以理解為，卷積神經網絡中的卷積核與反卷積神經網絡中的反卷積核是共享的。

為了衡量基于編碼一解碼對稱神經網絡對圖像壓縮重構的效果，引入損失函數并采用均方誤差表示損失函數，其表達式為式中：w為全連接層的網絡權重;β為池化層的網絡權重;K為卷積核參數;b為各層的偏置參數;m為訓練樣本的個數;tm為第m個樣本預測出來的真值;ym為第m個樣本在原來樣本中的值，也就是標準答案。由于本文網絡結構中并沒有涉及全連接層以及池化層，所以參數w和β忽略不計。

損失函數可以用來衡量網絡結構的好壞，損失函數越小說明網絡結構和參數越符合訓練樣本。因此訓練的過程就是不斷地改變參數，從而得到更小的損失函數的過程。在理想情況下，當我們取到損失函數的最小值時，就得到了最優的參數，記為

minE（θ）（3）

式中θ為所有參數的總稱。

3實驗分析

3.1實驗效果

基于編碼一解碼對稱神經網絡的圖像壓縮重構機理仿真采用MATLAB實驗平臺。在實驗中，所用到的訓練數據是MNIST數據庫，它包含70 000張手寫圖像數字的圖像，通常用60 000張圖像做訓練，再用剩下的10 000張做驗證，每一張都是28x28像素數的黑白圖像。考慮到訓練時間，本文只采用10 000張圖像，其中用于訓練的圖像為8 000張。如圖4所示，本文選用圖像數據庫中的數字“2”、數字“7”和數字“1”作為仿真對象，這些數字均為28像素×28像素的二值圖像。

本文所采用的壓縮方式為：首先確定圖像在尺寸上進行壓縮的倍數，本文進行兩倍的壓縮;其次調整圖像的尺寸，使調整后的尺寸能夠壓縮為原先的兩倍;再次以補零的方式進行填充，使圖像恢復為原先的尺寸，如圖5所示;最后將恢復后的低分辨率圖像作為編碼一解碼對稱網絡的輸入圖像來進行接下來的操作。

將編碼一解碼對稱神經網絡結構中的每個隱藏層中的節點個數設置為20個，那么會生成20個卷積濾波器以及20個特征圖像。以數字“2”為例，如圖6所示，圖中（a）為生成的卷積濾波器，（b）為卷積之后的圖像，（c）為卷積之后經過激活函數之后的特征圖像。圖7為經反卷積操作之后數字“2”、數字“7”和數字“1”的重構圖像。

3.2可行性分析

為了客觀精確地衡量基于編碼一解碼對稱神經網絡的圖像重構質量，這里引入了均方差（mean square error，MSE）和峰值性噪比（peaksignal-to-noise ratio，PSNR），可分別表示為：式中：MSE為原圖像與重構圖像之間的均方誤差;M、N分別為圖像的寬度和高度;R（i，j）為原始圖像對應像素點的值;F（i，j）為恢復圖像對應像素點的值;amax為圖像中最大像素點的值。PSNR值越大，說明兩幅圖越相似，即恢復的圖像質量越高。

表1分別列出了壓縮之后的低分辨率圖像和基于編碼一解碼對稱神經網絡的圖像高分辨率算法重構出來的圖像。經計算可以得到，低分辨率圖像的PSNR值比本文方法重構出來的PSNR值要低，說明低分辨率圖像經基于編碼一解碼對稱網絡的圖像高分辨率算法之后分辨率、清晰度都得到了提高，說明本文所提出的方法可行。

3.3效果對比

本文將基于編碼一解碼對稱神經網絡的圖像高分辨率重構算法與基于深層前饋卷積神經網絡的圖像重構算法進行比較。其中基于深層前饋卷積神經網絡的圖像重構算法主要用于消除圖像中的噪聲，同時其本身的體系結構也可以通過被訓練來重構壓縮圖像以及提高圖像分辨率。為了客觀地對這兩種算法進行評價，本文采用了相似度參數s，對于大小為MxN的圖像，s的數學表達式如下：

式中：x為原始圖像;x'為裁切過的重構圖像。

圖8比較了用不同重構算法得到的圖像，其中：（a）為原始圖像;（b）為基于編碼一解碼對稱神經網絡的圖像高分辨率重構算法重構出來的圖像（本文算法）;（c）為基于深層前饋卷積神經網絡的圖像重構算法重構出來的圖像。由此得出：（1）基于編碼一解碼對稱網絡的圖像高分辨率算法重構出來的圖像效果在圖像清晰程度、細節紋理方面要優于基于深層前饋卷積神經網絡的圖像重構算法重構出來的圖像;（2）經相似度公式計算得到基于編碼一解碼對稱網絡的圖像高分辨率算法重構出來的圖像相似度值為0.996 5，而基于深層前饋卷積神經網絡的圖像重構算法重構出來的圖像的相似度值為0.866 4。由此可見，基于編碼一解碼對稱網絡的圖像高分辨率算法重構出來的效果更佳。

4結論

本文提出了一種基于編碼一解碼對稱神經網絡的圖像高分辨率重構方案。首先將圖像在尺寸上進行兩倍的壓縮以獲取低分辨率的壓縮圖像，然后將此壓縮圖像作為輸入圖像，再經過編碼一解碼的對稱神經網絡的圖像重構算法重構圖像。本文采用MATLAB軟件進行仿真實驗，并進行了可行性分析和效果對比分析。實驗結果表明，基于編碼一解碼對稱神經網絡的圖像高分辨率算法能重構出清晰度更高，質量更好的圖像。