開溝深度定壓電液仿形控制系統設計與試驗

梁 方，雷淇奧，鄭思遠，王 鵬，郭 洲，劉 偉

（1. 華中農業大學工學院，武漢 430070；2. 農業農村部長江中下游農業裝備重點實驗室，武漢430070）

0 引 言

播深一致性是衡量播種機性能的重要指標之一，播深過淺或者過深不僅會影響種子的發芽率，還會造成株高不一致，進而影響后續植保、收獲等機械化作業質量[1-4]。播種深度主要由開溝器決定，播深一致性取決于開溝器仿形系統是否能夠實現開溝深度不隨地表起伏而變化[5-6]。

目前主要的仿形機構有機械仿形與電液（氣動）仿形。機械仿形通常利用彈簧形變，采用單點單桿鉸鏈式仿形機構、平行四桿仿形機構、多桿雙自由度仿形機構實現仿形功能，其中平行四桿仿形機構能夠保證仿形過程中開溝器始終垂直于地表，應用最廣[7-8]。但基于彈簧形變的平行四桿仿形機構并不能保證開溝深度完全一致，這是因為，理想土壤條件下（土壤物理參數一致），一定開溝深度對應的開溝豎直壓力是恒定的，而仿形過程中，隨著地表的起伏，彈簧會產生壓縮與伸長，彈簧對開溝器的豎直壓力亦會改變，導致開溝深度變化[9]。

為解決上述問題，出現了基于機-電-液一體化技術的電液仿形系統。國外學者從20 世紀70 年代開始電液主動式仿形技術研究[10]。Jensen 等[11]發明了一種采用壓力傳感器，通過單片機控制開溝器入土壓力，實現開溝器入土壓力恒定的播種機；Weatherly 等[12-13]研究了一種基于土壤含水量的種溝深度控制模型和系統；Pasi 等[14]基于ISO 11783 通訊協議，采用角度傳感器和遠程超聲測距傳感器檢測地表高度，控制電液比例減壓閥，輸出相應的壓力，從而控制開溝深度恒定，其播深控制精度在±10 mm，與傳統仿形相比，同一點的播深平均誤差降低1.7 mm； Kiani 等[15]開發了一種非接觸式播深控制裝置，利用超聲波傳感器測量出開溝深度，將深度信號傳遞給控制器后，調節液壓缸位移，實現播種深度一致。Burk等[16]設計了一種基于電機調整深度的播種機，用電機帶動絲杠實現播種深度和鎮壓壓力的調節。Nielsen 等[17-19]開發了一種犁刀開溝器深度控制系統，控制系統播深穩定性顯著高于傳統播種機，播深變異范圍降低了2 mm。在21 世紀初期，國內研究人員逐漸加強對主動式仿形開溝器的研究。李洪文等[20-22]發明免播機開溝深度調節裝置與自動控制系統，當開溝深度相對期望開溝深度過深或過淺（溝深低于 50 mm）時，其穩態響應時 間分別為0.48 與0.6 s，播深誤差均小于10 mm；Wen等[23]研發了一種基于PLC 的開溝仿形裝置，通過超聲波測距傳感器，將測得的距離信號與設定值進行比較，并通過控制比例閥來控制活塞的伸縮，從而調節開溝深度，響應時間在0.48～0.6 s，穩定誤差在1 mm 左右；趙金輝等[24]利用位移傳感器檢測開溝器位置信號，控制液壓缸伸縮，實現開溝深度控制，系統的響應時間為0.12 s，開溝深度穩定性系數在90%以上；黃東巖等[25]設計了一種利用壓電薄膜傳感器的開溝深度控制系統，能夠根據胎面的面積變化，計算作用在開溝器上的開溝反力，并以此控制空氣彈簧產生的壓力，使其輸出恒定的開溝壓力，保證播深一致；韓豹等[26]設計了一種基于超聲波測距的入土深度控制方法，調節液壓控制系統，實現鋤草裝置入土深度恒定控制，穩態響應時間為0.48 s，仿形精度±8 mm；賈洪雷等[27]設計了一種基于彎曲強度傳感的開溝深度控制系統，能夠通過傳感器采集數據并通過無線通訊手段將數據收集起來，對開溝器壓力進行調整，達到播深一致的效果，響應時間約為0.43 s，播深合格率在90%以上；付衛強等[28]利用安裝在開溝器上的銷軸傳感器檢測開溝壓力，并通過控制比例閥油壓來控制開溝器位置，播深合格率提高25%；劉平義等[29]設計了一種借助傾角傳感器實時測量車身傾斜角度并進行精確調整，實現底盤動態調平，為實現深度穩定性控制提供了借鑒。

綜上所述，電液主動仿形方法在保證播深一致性方面顯著優于機械被動仿形，多基于壓力、傾角、深度、位移、聲波、視覺等傳感器檢測信號，采用單片機、PLC等控制元件，控制液壓（氣動）缸、電機等執行元件，調節開溝器位移、壓力，實現開溝深度恒定控制。傳感器、控制元件、執行元件、控制對象不同，系統響應時間與誤差亦不相同。本文旨在設計一種開溝深度定壓電液仿形控制系統，采用PLC 控制液壓系統壓力輸出，實現開溝器入土壓力恒定控制，保證開溝深度一致，減少和降低基于壓力傳感器的電液仿形控制系統響應時間與穩態誤差，為電液仿形控制系統機械結構設計、液壓回路與液壓元件設計選型和控制系統建模仿真與調試提供理論支撐。

1 系統組成與工作原理及液壓元件選型

1.1 系統組成與工作原理

開溝深度定壓仿形系組成與原理圖如圖1 所示，主要包括機械系統、液壓系統、控制系統。機械系統由開溝器、平行四桿機構組成，液壓系統由液壓缸、電磁換向閥、電液比例減壓閥、節流閥、變量泵、溢流閥、液壓油箱等組成，控制系統由西門子S7-200 主機（包括CPU224XP、數字量/模擬量輸入輸出模塊EM235 等）、壓力傳感器、變送器、電流放大器、DC24V 電源組成。

系統開始工作前，根據農藝要求與土壤特性，確定一定開溝深度所需的壓力值，并將該理論值輸入PLC中。按下啟動鍵SB1，接通電源，電機啟動，帶動液壓馬達，系統開始工作。開溝過程中，位于雙圓盤開溝器上的壓力傳感器實時檢測開溝壓力，并通過變送器轉換為電流信號存儲到PLC 中，控制元件將該信號與理論壓力值進行比較并作差，利用差值信號控制輸出電流大小，經過電流放大后，驅動電液比例減壓閥YV3，實現閥口出口壓力與電流信號比例控制，保證開溝器入土壓力恒定。當地表平整、開溝壓力恒定，電磁閥YV1、YV2、YV3 失電，3 個閥的左位接入回路，油路不通，變量泵泵出的油液經溢流閥流回油箱；當地表凸起、開溝壓力增大，電磁閥YV1、YV2 、YV3 得電，右位接入回路，油路接通，由于液壓缸中的壓力值大于電液比例減壓閥的壓力設定值，先導閥打開，在保證減壓閥出口壓力恒定的同時，減壓閥出口處的油液通過先導閥流回油箱，液壓缸收縮，開溝器抬起，開溝壓力降低，直至恢復到設定值，系統恢復到穩定狀態。反之，當地表凹陷、開溝壓力降低，電磁閥YV1、YV2、YV3 得電，右位接入回路，油路接通，由于液壓缸中的壓力值小于電液比例減壓閥的壓力設定值，油液進入液壓缸，液壓缸伸長，開溝器下降，入土壓力增加，直至恢復到設定值，系統恢復到穩定狀態。按下SB2 后變量泵停止工作，按下SB3、SB4，電磁換向閥YV1、YV2 右位接通，手動抬起開溝器，避免設備放置時開溝器觸地受壓，對機械與液壓系統進行保護，完成后再切斷電源，系統恢復到初始狀態。

圖1 系統組成 Fig.1 Components of system

1.2 系統液壓元件選型

對于播種機械，開溝深度一般在10～80 mm ，取最大開溝深度80 mm，開溝仿形量定為±50 mm[30]，為便于實現伸縮仿形，地表平整時，液壓缸處于中間行程（最大位移一半）位置，則液壓缸的行程應大于130 mm，MOB40×200LB 雙作用活塞桿行程為200 mm，滿足要求。單個開溝器入土壓力一般在20～200 N，本文取最大值F=200 N[30-31]，根據液壓缸受力平衡有：

式中P1為電液比例減壓閥出口壓力，MPa；P2為油缸出油口背壓，取0.5 MPa；D 為活塞直徑，40 mm；d 為活塞桿直徑，20 mm。計算可得P1為0.534 MPa，在0～2 MPa范圍，處于電液比例減壓閥壓力輸出范圍內。節流閥起節流調速作用，降低液壓缸運動速度，減少震動，并限制電液比例減壓閥入口壓力，可通過調節手柄，調節節流閥的過流面積，出口壓力設定為2～2.4 MPa，使得電液比例減壓閥入口壓力既不超過入口最大壓力2.4 MPa，又保證輸出壓力達到0～2 MPa 最大范圍。溢流閥起保壓限壓作用，保證進入節流閥的壓力小于額定壓力，并保證系統安全，為保證節流閥有較好的剛度，進出口壓差一般設定在0.15～0.4 MPa，而節流閥出口壓力設定在2～2.4 MPa，則節流閥進口壓力等于出口壓力與壓差之和，為2.15～2.8 MPa，即為溢流閥溢流壓力設定值。液壓泵的額定壓力應大于2.8 MPa，VP-12-FA3 變量泵的額定工作壓力在4～7 MPa，滿足輸出壓力要求。液壓元件參數如表1 所示。

表1 液壓元件參數表 Table 1 Parameters of hydraulic elements

實際工作中應選用具有連續液壓輸出的拖拉機作為動力源，且液壓接頭輸出額定流量與壓力均需大于泵的流量5.3～12 L/min 與壓力4～7 MPa。以John Deere 1024拖拉機為例，其液壓輸出系統額定流量為24.4 L/min，額定工作壓力為19 MPa，滿足液壓系統動力源要求。

2 系統穩定性判別與單位響應分析

2.1 系統傳遞函數

2.1.1 液壓缸流量連續性方程與受力平衡方程

假定液壓管路中壓力損失和管道動態可以忽略不計，同時液壓缸內部處處壓力處相等，油液的溫度和彈性模量是常量。基于以上假設，閥控液壓缸的流量連續性方程為[32]

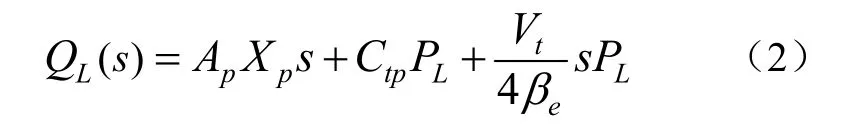
式中Ap為活塞的有效面積，m2；Xp為活塞的位移，m； Ctp為總泄漏系數，%；QL為負載流量，m3/s；PL為負載壓力，Pa；Vt為總壓縮體積，m3；βe為有效體積彈性模量，Pa；s 為復變數。

液壓動力元件會受到負載（慣性力，黏性阻尼力，彈性力和外負載力）的影響，根據活塞受力平衡有：

式中mt為活塞及負載折算到活塞上的總質量，kg； Bp為活塞及負載的黏性阻尼系數，Ns/m；K 為負載彈簧剛度，N/m；FL為作用在活塞上的負載，N。

2.1.2 電液比例減壓閥的流量連續方程與壓力輸出方程

電液比例減壓閥流量方程為

電磁比例減壓閥的傳遞函數比較復雜，應用過程中可將電磁比例減壓閥的傳遞函數簡化為一個二階環節，其傳遞函數為[23]

式（4）～（5）中，P(s)為輸出壓力，Pa；I(s)為輸入電流，A；Ki為電液比例減壓閥增益，Pa/A；ωn為固有頻率，rad/s；εn為阻尼系數；ωv為轉折頻率，rad/s； K0為剛度系數，Nm/s；Qv為流量，m3/s。

2.1.3 平行四桿仿形機構傳遞函數

設沿著活塞桿方向的力為FL，開溝器自身重力G，土壤對開溝器的豎直反力為FN，由于平行四桿較長，上下仿形量相對稈長較小，液壓缸與地表間的安裝傾角變化不大，因此可以近似認為液壓缸活塞桿與水平面的傾角α 不變，以液壓缸回轉中心為原點建立力矩平衡方程：

式（6）～（7）中，L1為豎直反力力臂，mm；L2為活塞桿推力力臂，mm；α 為液壓缸與水平方向夾角，（°）；KSG為四桿機構的增益。

此外，系統中還有壓力傳感器、壓力變送器、放大電路等環節，由于這些環節的響應速度都高于液壓缸的響應速度，因此均可視為比例環節，設Ks為壓力傳感器增益，Kai為放大電路增益。

2.1.4 系統傳遞函數

傳感器輸出的電流信號，控制電液比例減壓閥的輸出壓力，根據電液比例減壓閥輸出流量與壓力同液壓缸輸入相等，建立經電液比例減壓閥后液壓缸輸出壓力與出入電流關系如圖2 所示。

圖2 液壓缸輸出壓力與輸入電流關系方框圖 Fig.2 Block diagram of the relationship between the output pressure of the Hydraulic cylinder and the input current

根據圖2，聯立方程（1）～（4），求出液壓缸輸出壓力與輸入電流的關系函數。

將平行四桿、壓力傳感器，壓力變送器，電子放大電路等環節代入（8），得到系統輸出壓力與輸入電流關系如圖3 所示。

根據圖4，解得系統的傳遞函數為

根據選定的液壓元件型號參數、機械結構參數[33]，系統傳遞函數參數值如表2。

圖3 控制系統輸出壓力與輸入電流關系方框圖 Fig. 3 Block diagram of the relationship between the output pressure of the control system and the input current

表2 系統傳遞函數參數值 Table 2 Parameters of system transfer function

2.2 系統穩定性判別

利用特征根的位置來判斷系統的穩定性。根據式（14），求得系統閉環傳遞函數3 個極點S1、S2、S3分別為：S1=-80.6+209.98i，S2=-80.6-209.98i，S3=-0.28，i 為虛數，i2=-1。均在復平面左側，因此可以判斷系統穩定。

2.3 系統單位階躍響應分析

工作中，所需的開溝力值是直接寫入到PLC 存儲單元 中，是不隨時間變化的輸入量，因此采用單位階躍信號分析系統的響應特性。根據系統閉環傳遞函數，按照系統穩定性的要求，加入PID 控制環節，采用試湊法確定PID 的3 個調節常數，當比例、積分、微分比例增益系數分別設定為5、200 和0.2 時，系統達到穩態，響應快，在MATLAB中建立Simulink 模型，其單位階躍響應曲線如圖4 所示。

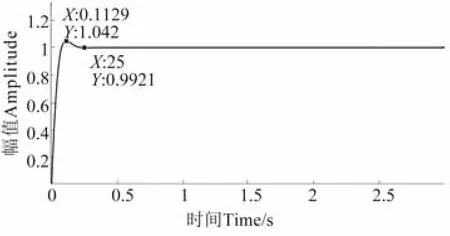
圖4 單位階躍響應曲線 Fig.4 Response curve of unit step

由圖4 可見，系統單位階躍響應峰值時間為0.113 s，最大值幅值為1.042，穩態值為0.9921，超調量為5.02%，穩態響應時間為 0.25 s，穩態誤差為0.79%。仿真結果表明，控制系統能夠快速穩定的實現恒定壓力輸出，系統設計方案可行。

3 系統調試與試驗

3.1 試驗原理與裝置

試驗原理與裝置如圖5 所示。壓力傳感器安裝在左側仿形缸與右側模擬缸之間，用于檢測開溝壓力。仿形所需的壓力由PLC 中的存儲值設定。地表起伏模擬系統由變量泵、溢流閥（作定壓閥）、節流閥、三位四通電磁換向閥與模擬液壓缸組成，節流閥與溢流閥組成進口節流調速回路控制液壓缸輸出壓力，模擬一定開溝深度下所需的開溝壓力。調節三位四通電磁換向閥，控制液壓缸的伸縮量，模擬地表起伏狀況。當YV4 通電，三位四通電磁換向閥左位接通，液壓缸伸長，模擬地表凸起；當YV5 通電，三位四通電磁換向閥右位接通，液壓缸收縮，模擬地表凹陷。

圖5 試驗原理與裝置 Fig.5 Principle and device of experiment

3.2 壓力傳感器標定

將不同質量的砝碼（理論值）加載到壓力傳感器上，讀取PLC 中存儲的數字量，轉化為對應的力值，將該值作為測量值，得到測量值與理論值關系如圖6 所示。擬合直線的擬合度為0.9958，傳感器精度可靠。

圖6 壓力傳感器標定結果 Fig.6 Calibration results of pressure sensor

3.3 電液比例減壓閥輸入輸出關系

電液比例減壓閥根據輸入電流信號按一定關系輸出油液壓力，電流信號由PLC 內部經過D/A 轉換輸出，再通過電流放大器，驅動電液比例減壓閥工作。因此，數字量與電液比例減壓閥輸出壓力關系是控制輸出壓力大小的依據。PLC 模擬量輸出模塊EM235 的數字量范圍為0～32 000，對應輸出電流為0～20 mA，程序中，數字量存儲在AQW0 單元中，改變 AQW0 中的數值，建立數字量與電液比例減壓閥輸出壓力的關系，結果如圖7 所示。

由圖7 可見，電液比例減壓閥的輸出壓力值在模擬量輸入值小于6 400 時為0，也就是說0～6400 為死區，而在模擬量大于22400 時，電液比例減壓閥的輸出壓力達到最大值2 MPa。在模擬量為9 600～22 400 區間內，該電液比例減壓閥的輸出壓力與模擬量輸入值成線性關系，MATALAB 擬合得到y=134.8x-1 058，R2為0.978 2，表明用PLC 控制電液比例減壓閥控制液壓回路中的壓力可行，根據電液比例減壓閥輸入電流數字量與輸出壓力關系，將模擬量輸入的上下限分別設定為6 400與22 400，以避免出現死區電流以及飽和電流的情況。

圖7 電液比例減壓閥輸入電流數字量與輸出壓力關系圖 Fig.7 Relationship between digital input current and output pressure of electro-hydraulic proportional pressure reducing valve

3.4 試驗過程與結果分析

通過編寫程序，設定液壓缸的仿形輸出壓力值，根據調定范圍在20～200 N，分別選取20，80，140，200 N的開溝壓力，根據10～80 mm 播深，選取10、20、30、40、50、60、70 和80 mm 仿形深度分別進行試驗。啟動仿形系統，此時仿形缸處于最長伸長狀態，模擬缸處于最短收縮狀態；啟動地表起伏模擬系統，緩慢增大溢流閥壓力設定值，直至達到2 MPa；調節節流閥，逐漸增大節流閥閥口開度，讓模擬缸伸長50 cm 以上（便于后期模擬凹陷）；系統穩定后，控制電磁換向閥通斷電，首先使模擬缸伸長到50 mm 處；當模擬地表凸起，接通YV4，控制液壓缸伸長到指定仿形深度處（如60 mm），再接通YV5，讓模擬缸收縮，回到50 mm 狀態，為下一組試驗做準備，依此完成所有播種深度的試驗；在仿形缸從非穩態過渡到穩態過程中，通過PLC 內部計時器記錄系統誤差從不為零（地表起伏變化引起開溝壓力變化）到變為零（穩定狀態）的時間間隔，即為系統的響應時間；讀取壓力傳感器的數值并與設定值作差，即為穩態誤差。最終得到仿形系統穩態誤差與響應時間如表3 所示。

由表3 可見，在20～200 N 的開溝力值10～80 mm 的開溝深度范圍時，平均響應時間為0.27～0.36 s，最大響應時間為0.4 s，平均穩態誤差為1.4～1.8 N，最大穩態誤差為2.7 N，標準偏差為0.78%～ 6.94%，能夠實現恒壓力輸出。仿形量越大響應時間越長，開溝壓力越大，響應時間越短。仿形量與開溝壓力對穩態誤差幾乎無影響，但平均標準偏差隨著開溝壓力的增大而減小，說明系統在較大開溝壓力下工作，響應精度更高。與仿真結果相比，試驗的平均響應時間高出4%～44%（試驗結果為0.27～0.36 s，仿真結果為0.25 s），最小標準偏差與穩態誤差相差0.01%（試驗結果為0.78%，仿真結果為0.79%），在誤差可接受范圍內，驗證了系統模型的可靠性與準確性。

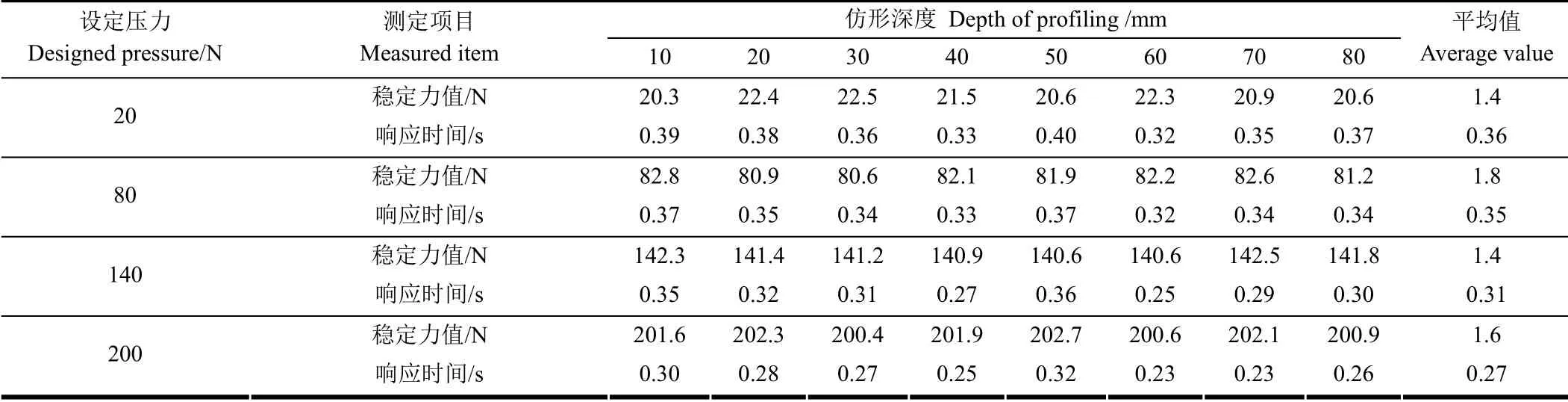
表3 系統穩態誤差與響應時間 Table 3 Steady-state error and response time of system

4 結 論

1）本文設計了開溝深度定壓電液仿形控制系統，確定了液壓系統回路、液壓元件型號與參數以及控制元件類型與參數、硬件連接和相應的軟件程序，實現了播種開溝恒定壓力輸出；

2）分別建立系統液壓缸、電液比例減壓閥、平行四桿機構及壓力傳感器、壓力變送器、信號放大器等系統組成環節的傳遞函數，得到系統閉環傳遞函數，利用MATLAB 求解傳遞函數的特征根，求得系統極點都在復平面的左側，系統穩定，對系統在單位階躍響信號下的響應行進分析，當PID 控制的比例、積分、微分增益系數分別設定為5、200 和0.2 時，系統的超調量為5.02%，響應時間為0.25 s，穩態誤差為0.79%，表明控制系統能夠快速穩定的實現恒定壓力輸出，系統設計方案可行；

3）在20～200 N 的開溝力值、10～80 mm 的開溝深度下，試驗結果表明，系統平均響應時間在0.27～0.36 s，最大響應時間為0.4 s，系統平均穩態誤差在1.4～1.8 N，最大穩態誤差在2.7 N，標準偏差在0.78%～ 6.94%，與仿真結果相比，試驗的平均響應時間高出4%～44%，最小標準偏差與穩態誤差相差0.01%，在誤差可接受范圍內，驗證了系統模型的可靠性與準確性。