基于信息融合的概率矩陣分解鏈路預測方法

王智強 梁吉業, 李 茹,

1(山西大學計算機與信息技術學院 太原 030006)2 (計算智能與中文信息處理教育部重點實驗室(山西大學) 太原 030006)

社交信息(social-information)網絡[1](如微博，Twitter等)，不僅包含用戶間的網絡結構，同時存在大量用戶所分享的文本信息，具有規模大、動態變化、信息混雜等大數據通常所具有的特點，屬于典型的網絡大數據[2].圖1為一個帶有文本信息的Twitter數據集可視化示例，圖1(a)中的網絡代表用戶間關注被關注(follwingfollowed)的有向網絡，圖1(b)分別對應網絡中每個用戶所分享的Tweet文本信息.

Fig. 1 A Twitter example of social-information network with text information圖1 帶有文本信息的社交信息網絡Twitter示例

鏈路預測作為網絡數據挖掘中一項基本挖掘任務[3]，它在許多研究及應用領域發揮著重要作用.例如對于網絡演化[4-5]、網絡數據補齊[6-7]等問題的研究具有重要意義，同時在推薦[8-9]、生物信息[10]等領域發揮著重要應用價值.鏈路預測的研究目標[11-13]是預測當前網絡中節點之間是否存在缺失的連邊或是未來網絡中是否會產生新的連邊.本文將面向社交信息網絡，針對其信息混雜特點，從信息融合角度研究社交信息網絡中的鏈路預測問題.

目前針對鏈路預測的研究已有來自計算機、物理、生物等許多不同領域的研究者，針對不同的網絡提出針對性的鏈路預測方法.現有鏈路預測方法通常從網絡的拓撲結構出發，通過定義網絡中節點間的拓撲度量或通過建立網絡的統計學習模型來獲得網絡中節點間鏈路的可能性.已有基于度量的方法中，如基于鄰居信息[14-16]、路徑信息[17-18]、隨機游走[19-20]等度量方法考慮了網絡中節點間的拓撲相似度距離.基于學習的方法如層次網絡模型[6]、隨機塊模型[21-22]、潛在特征模型[23-25]及矩陣分解模型[26-27]等從網絡結構全局出發來學習節點間的鏈路可能性，相比基于度量的方法具有更好的適用范圍.

盡管當前針對不同網絡的鏈路預測方法研究已經取得了許多進展，但面向信息混雜的社交信息網絡的鏈路預測研究仍然有待深入.用戶所分享的文本信息作為眾多形式信息中廣泛存在的數據載體，如何充分利用用戶所分享的文本信息來提高面向社交信網絡的鏈路預測是一個挑戰.社交信息網絡中，信息的傳播依賴于網絡中節點間的關注被關注關系，1條Tweet會從其發布者傳遞到其跟隨者(關注者)，同時在Tweet的傳播過程中也會影響到網絡中鏈路關系的形成.如當用戶對某條Tweet十分感興趣時，該用戶將有一定可能性成為此信息發布者的關注者.當然除此之外，社交信息網絡中鏈路的變化與信息傳播間相互影響的情況還有許多.從建模角度來講，如何將拓撲的網絡結構與非拓撲的文本信息進行融合建模是面向社交信息網絡鏈路預測的關鍵.

本文試圖從信息融合的角度，在抽取用戶主題信息的基礎上，構建用戶間的主題相似網絡，并提出融合用戶間關注被關注網絡與主題相似網絡的概率矩陣分解模型；進一步基于模型學習到的用戶潛在特征表示與用戶間的鏈路參數計算用戶間的鏈路可能性，實現面向社交信息網絡的鏈路預測.

1 相關研究

目前針對網絡中鏈路預測問題所提出的方法主要包括：基于度量的方法、基于分類的方法、基于概率圖的方法及基于矩陣分解方法等.

1.1 基于度量的方法

通過定義網絡節點間拓撲或非拓撲上的度量來對網絡節點間的連邊可能性進行打分是鏈路預測中最為常見的方法.拓撲度量是利用網絡中節點對間的各種拓撲信息來定義，如基于鄰居信息的度量有公共鄰居(common neighbors， CN)[15]、Jaccard[28]、大度節點有利(hub promoted， HP)[29]、大度節點不利(hub depressed， HD)[13]、鄰居貢獻(adamic-adar， AA)[14]、偏好性(preferential attachment， PA)[16]以及資源分配(resource allocation， RA)[7]等.Katz[17]，Local Path[18]，FriendLink[30]等方法利用了網絡中節點間路徑信息；平均通勤時間(average commute time， ACT)[13]、余弦相似度時間(cosine similarity time， CST)[19]、重啟隨機游走(random walk with restart， RWR)[31]、SimRank[20]、局部隨機游走(local random walk， LRW)[32]等則是基于網絡隨機游走過程來定義.社交網絡中常見的非拓撲信息包括用戶的簡介、標簽、文本信息、關鍵詞等[25,33-35].Matthew等人[33]基于用戶標簽進行用戶相似度度量.Prantik等人[35]基于關鍵詞分析社交網絡用戶的相似度.已有基于拓撲或非拓撲信息度量的鏈路方法通常與具體網絡的性質、領域等密切相關，單一度量方法往往容易領域受限.

1.2 基于分類的方法

基于分類的方法是將鏈路預測看作二分類問題，其中將網絡中存在連邊的節點對看作正例，沒有連邊的節點對看作負例.在建立分類模型時，許多分類器如支撐向量機(support vector machine， SVM)、邏輯斯蒂回歸(logistic regression， LR)、k近鄰(k-nearest neighbor，kNN)、樸素貝葉斯(Naive Bayesian， NB)等被用在鏈路預測問題中，而影響預測結果的關鍵因素之一是特征選擇問題.Sa等人[36]利用節點對間的公共鄰居、Jaccard、鄰居貢獻、偏好性及局部路徑等來作為分類的特征；Lichtenwalter等人[37]提出了一種基于節點搭配的局部拓撲特征；Leskovec等人[38]利用節點的度和三元組特征來實現鏈路預測；Chiang等人[39]擴展了Leskovec等人[38]的工作，提出從更長的網絡環路中來抽取拓撲特征.同1.1節中的度量方法類似，分類模型的特征選擇同樣容易受網絡性質、領域等影響，且類的非平衡性問題也是制約基于分類模型進行鏈路預測的一個瓶頸.

1.3 基于概率圖模型的方法

概率圖模型是對網絡數據進行建模的一類重要方法，它能夠從網絡全局出發揭示深層次的網絡結構與性質.Clauset等人[6]提出一種層次網絡模型，將網絡建模為一種層次結構，其中葉子節點對應網絡節點，中心節點對應不同葉子節點間的鏈路概率.隨機塊模型[21-22]假設網絡節點可以被劃分為不同的組，節點間的鏈路可能性由節點所在的組決定.潛在特征模型[23-24]是一種產生式模型，它假設網絡中的節點可以用潛在特征向量來表示，網絡中連邊的產生式基于節點的潛在特征表示和連邊產生的分布假設.已有網絡概率圖模型通常能夠獲得較好的鏈路預測效果，然而此類模型具有較高的計算復雜度，難以適用于較大規模的網絡，且難以擴展到具有混雜信息的網絡中.

1.4 基于矩陣分解的方法

矩陣分解方法是通過對網絡的鄰接矩陣進行低秩近似來解決鏈路預測問題.目前，矩陣分解方法如奇異值分解(singular value decomposition, SVD)[40]、非負矩陣分解(non-negative matrix factorization, NNMF)[41]及概率矩陣分解(probabilistic matrix factorization, PMF)[42]等已被廣泛用于推薦系統.相比基于推薦方法，基于矩陣分解的網絡鏈路預測方法研究仍有待深入.Menon等人[26]通過在矩陣分解時加入排序損失來克服鏈路預測中的非平衡問題，在鏈路預測準確率與效率2方面都獲得了較好的結果.Zhai等人[27]提出一種結合矩陣分解和自編碼的鏈路預測方法，獲得了較好的鏈路預測效果.矩陣分解方法通常可以采用隨機梯度下降等快速算法來實現，容易適用于大規模的網絡數據[26].總體來講，矩陣分解方法在解決網絡鏈路預測問題時通常具有時間與效果兩方面的綜合優勢，但目前仍缺乏面向帶有混雜信息網絡的矩陣分解鏈路預測方法.

本文試圖從矩陣分解方法入手，通過結合社交信息網絡中用戶的文本內容信息，建立一種能夠融合用戶網絡結構和文本信息的矩陣分解方法，在此基礎上實現面向社交信息網絡的鏈路預測.

2 融合的概率矩陣分解模型

社交信息網絡既包含用戶間的網絡拓撲結構信息，同時還包括豐富的用戶文本信息.本文基于概率矩陣分解模型來建模的目標是為了將2種信息融合在統一的概率分解框架下，以獲得新空間下融合2種信息的用戶表示，將此模型稱為：融合概率矩陣分解模型(fusion probability matrix factorization, FPMF).以下分3小節來介紹FPMF模型.為便于理解，在此將文中涉及的主要符號匯總為表1：

Table 1 The List of the Main Notations表1 主要符號列表

2.1 用戶主題相似網絡構建

同質性[43-44]是社交網絡中普遍存在的一種特性，它指社交網絡中具有相似性的人之間容易產生鏈接，而存在鏈接的人之間也會因為相互影響而具有一定相似性.同質性說明社交網絡中鏈路的產生與用戶相似性之間具有一定相關性.本節試圖從用戶的主題相似度出發，利用社交信息網絡中用戶分享的文本信息抽取用戶主題表示，并定義用戶間的主題相似度，進一步基于主題相似度構建一種用戶間的主題相似網絡.

為獲取用戶主題信息，我們將每個用戶歷史所分享的所有微博信息看作一個文檔，n個用戶組成包含n個文檔的文檔集合D.基于潛在狄利克雷(latent Dirichlet allocation, LDA)主題模型[45]，抽取每個用戶的主題分布表示(見4.1節關于數據預處理的內容).

由于LDA模型所抽取的用戶主題向量是一種多項分布表示，而KL(Kullback-Leibler)[46]散度適合于度量分布之間的距離，因此首先采用了KL散度來度量用戶間的主題分布距離；然后基于指數函數exp(-x)將此距離映射到(0,1)之間作為相似度度量.考慮到KL度量是一種非對稱的距離度量，對其進行了對稱化處理.具體地，用戶主題相似度定義如下：

(1)

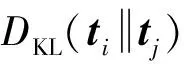
基于主題相似度(式(1))，定義用戶之間的主題相似網絡如下：

定義2. 用戶主題相似網絡.用四元組NS=(V,E,S,Sthr)表示用戶主題相似度網絡.V表示此網絡的節點集合；E表示網絡中邊的集合；S表示該網絡的鄰接矩陣，其中矩陣S中每個元素的取值Si j代表用戶i與用戶j之間的主題相似度；Sthr表示構建主題相似網絡的稀疏化參數，即當用戶間的主題相似度值大于Sthr時，為其建立一條無向的邊，反之不建立邊，因此，Sthr的取值直接影響主題相似網絡的稀疏性，Sthr越大網絡越稀疏.

如圖2所示，一個包含282個用戶的Twitter數據集的主題相似網絡構建過程.圖2中從左至右分別表示用戶的Tweets信息、主題向量以及用戶間的主題相似網絡，其中網絡稀疏化參數Sthr=0.7.需要提及的是，對用戶主題相似網絡進行稀疏化，主要基于2方面考慮：一方面在利用用戶大量的文本信息來計算用戶間主題相似度時不可避免會有噪聲，稀疏化設置使后續建模中只關注相似性較大的連邊，緩解噪聲影響；另一方面，網絡稀疏化能夠減小模型的計算復雜度.稀疏化參數Sthr的具體選取將在實驗部分(4.4.3節)進行詳細實驗分析與討論.

Fig. 2 The construction process of the users’ topic similarity-based network圖2 用戶主題相似網絡構建

2.2 FPMF模型

從概率產生式角度，網絡NA和NS的產生式過程可以用3個步驟來描述：

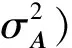
其對應的概率圖如圖3所示.

Fig. 3 The probabilistic graph model of FPMF圖3 FPMF模型概率圖表示

在網絡產生式過程的第1步，網絡中每個節點i的潛在向量Ui∈1×L從高斯先驗分布N(0,中產生，網絡中所有節點的潛在特征矩陣U的先驗分布滿足

(2)

(3)

在生成網絡節點的潛在特征表示矩陣U和網絡NA的鏈路關系矩陣參數W的基礎上，進一步產生網絡NA和NS中的連邊與非連邊.見網絡產生式過程的第3步：網絡NA中任意節點對i,j間的連邊Ai j=1或非連邊Ai j=0是基于高斯分布N(gA(Ui,Uj),產生的，即

(4)

其中，gA(Ui,Uj)是為了度量網絡NA中任意節點對i,j間鏈路關系而定義的關系函數：

(5)

基于網絡NA中每對節點連邊與非連邊的產生過程，其概率分布可以記為

在此統一的概率產生式框架下，主題相似網絡NS中任意節點對i,j連邊與不連邊同樣基于一個高斯分布N(gS(Ui,Uj),而產生，即

(7)

其中，gS(Ui,Uj)是度量主題相似網絡NS中任意節點對i,j之間的鏈路關系度量函數，定義如下：

(8)

依據第3步中主題相似網絡NS的產生過程，其概率分布表示為

基于網絡NA和網絡NS的整個產生過程，融合概率矩陣分解的目標就是通過極大化網絡中節點的潛在特征表示U和鏈路參數矩陣W的后驗分布，來估計極大后驗下的U和W，即

(10)

由于網絡NA和NS是已知可觀察的，式(10)中的后驗分布正比于如下聯合概率分布：

(11)

因此，式(10)等價于

(13)

將式(2)(3)(6)(9)帶入式(13)，并取對數形式，可以推導出式(13)的優化目標等價于最小化如下目標函數：

,

(14)

.

(15)

目標函數的局部最小值可以采用梯度下降方法進行求解[47]，參數U和W的梯度下降公式為

(16)

(17)

以包含有282個用戶的社交信息網絡Twitter為例(如圖4)，圖4(a)為用戶之間的關注被關注網絡NA，圖4(b)為構建的用戶主題相似網絡NS.模型的意義在于：通過共享同一個網絡節點的潛在特征表示U，將網絡NA鄰接矩陣A的近似A≈UWUT和網絡NS鄰接矩陣S的近似S≈UUT融合在一個矩陣分解模型中.

Fig. 4 Sketch of the FPMF model圖4 FPMF模型示意圖

2.3 模型復雜度分析

由于矩陣A與矩陣S的稀疏性，A與U乘積的計算復雜度為O(ηAL)，其中ηA為稀疏網絡A中非0項個數；類似地，SU的乘積復雜度為O(ηSL)，ηS為矩陣S中的非零項個數；剩余部分乘積的計算復雜度為O(nL2).因此，模型求解時每次迭代的總時間復雜度為O(ηAL+ηSL+nL2).由于網絡的稀疏性，網絡中邊的個數幾乎是網絡節點數的倍數，則有ηA=O(n)與ηS=O(n)，因此模型每次迭代的復雜度理論上與網絡節點個數成近似的線性關系.

3 基于FPMF的鏈路預測

基于FPMF模型，能夠學習到網絡NA和網絡NS中節點共同的潛在特征表示U以及網絡NA中的鏈路參數矩陣W.依據模型中所描述的網絡NA的產生式過程，對于任意節點對i,j間產生連邊的概率可以計算如下：

P(i,j=1)=P(Ai j=1|Ui,Uj,W,
.

(18)

算法1. 基于FPMF模型的鏈路預測.

輸入：關注網絡鄰接矩陣A、主題相似網絡鄰接矩陣S；

輸出：鏈路預測的AUC(area under the receiver operating characteristic)值和Accuracy值.

① 初始化：網絡節點的潛在特征矩陣UN×L，網絡A的鏈路參數矩陣UL×L，L=integer?n；

② REPEAT

UnewUold-γ，見式(16)；

WnewWold-γ，見式(17)；

③ UNTIL CONVERGENCE

END FOR

⑤ 基于P值對所有未知節點對進行排序；

⑥ 基于排序計算鏈路預測結果的AUC值和Accuracy值，見式(19)(20)；

⑦ RETRUN:AUC和Accuracy.

4 實驗及結果分析

4.1 實驗數據

驗證本文方法所需的數據集需同時包含用戶間的網絡結構和用戶的文本信息，本文采用了兩種社交信息網絡數據集，Weibo和Twitter，均來源于唐杰團隊在文獻[48]中所共享的數據.由于原始數據集中有許多用戶沒有發表過或者很少發表微博Tweets，難以滿足用戶主題抽取需求，因此實驗中僅抽取了網絡中發表或轉發微博Tweets數量超過100條的用戶.最終在2個原始的數據集中分別抽取了4組子數據集：Weibo 1，Weibo 2，Twitter 1，Twitter 2，如表2所示：

Table 2 Datasets表2 數據集

針對中文數據集Weibo 1和Weibo 2的微博文本預處理主要包括：首先去除掉其中的非文本字符，如數字、表情符號等；然后進行分詞和停用詞去除處理，并對用戶發表或轉發微博時經常會出現的“分享”、“轉發”、“微博”等頻繁詞也進行去除處理.針對Twitter數據集，由于文獻[48]中的原始數據集已對Tweets進行了預處理，本實驗中不作進一步處理.

在數據集預處理基礎上，為獲得用戶主題表示，我們將網絡中每個用戶所有發表或轉發微博Tweets看作一個文檔，然后采用Scikit-learn[49]工具包所提供的LDA主題抽取工具對網絡用戶的主題進行抽取，獲得用戶的分布式主題向量表示.

4.2 實驗設置與評價指標

依據鏈路預測相關文獻通常采用的實驗設置[6,13,27]，實驗中將數據集中的網絡劃分為訓練集和測試集.具體地，本實驗將網絡劃分為90%∶10%，其中90%的部分作為訓練集，10%作為測試集，且劃分時分別執行獨立隨機劃分5次，每次隨機劃分保證訓練集網絡的連通性.

結果評價時，采用了2種評價指標：一是鏈路預測中最為常用的AUC評價指標[13]；另一種是鏈路預測結果的準確率指標Accuracy.

1)AUC指標

AUC是指ROC曲線(receiver operating char-acteristic curve)下方的面積.實際計算時可以采用抽樣的方法來計算AUC值[13,50]，即在測試集中隨機選擇一條邊的分值比在不存在的邊集合中隨機選擇一條邊的分值高的概率.具體計算公式為

(19)

其中，n′表示隨機從測試集與不存在邊的集合中抽取n次出現n′次抽取的測試集邊的分值大于沒有邊的分值，而n″是分值相等的次數.

2)Accuracy指標

Accuracy是指預測的準確率，其計算公式為：

(20)

其中，L表示測試集中共有L條邊，k表示在排序前L個節點對中正確的個數.

4.3 比較方法

為驗證本文方法在社交信息網絡中鏈路預測的有效性，設置了2部分比較實驗：一是本文方法與2種基線(baseline)方法作比較；二是本文與已有相關文獻中常見的鏈路預測方法進行比較.

4.3.1 基線方法

基線方法的設定是為了驗證本文融合模型將2種信息(網絡和主題)在融合后相比融合前的優勢.具體設定了2種基線方法：

1) 基本概率矩陣分解的方法

基本概率矩陣分解的方法是只針對網絡結構進行概率矩陣分解，即只針對網絡A進行概率矩陣分解，其形式化表示為：

(21)

2) 基于主題相似度量的方法

基于主題相似度量的方法是利用用戶的主題信息，通過度量用戶間主題相似度的大小進行鏈路預測.用戶間主題相似度的計算見式(1)，此方法記為TS(topic similarity).

4.3.2 已有的鏈路預測方法

1) Katz

Katz是在已有文獻[13]中被驗證表現最好的方法之一.對于給定網絡中的節點對i,j，Katz方法定義如下：

(22)

2) 公共鄰居(CN)[13]

CN指標是鏈路預測中非常廣泛使用的指標，它在許多網絡也被驗證通常具有良好的表現[13].由于社交信息網絡中用戶之間是關注與被關注的關系，用戶之間具有不同類型的鄰居，即關注者或被關注者.因此，在定義用戶間CN指標時利用了不同類型的鄰居，最終采用4種CN指標：CN1，CN2，CN3，CN4，如表3所示：

Table 3 CN Indexes表3 CN指標

表3中Γ+(i)表示社交信息網絡中關注用戶i的用戶集合，Γ-(i)表示被用戶i關注的用戶集合，|Γ+(i)|和|Γ-(i)|分別代表集合Γ+(i)與Γ-(i)的用戶數量.

3) 偏好性(PA)

偏好性指標PA也是在社交網絡中常用的鏈路預測方法[13].給定網絡中用戶i與用戶j的鄰居數量，PA指標等于2個用戶鄰居數據的乘積.同CN類似，依據社交信息網絡中不同類型的鄰居，采用了4組不同的PA指標：PA1，PA2，PA3，PA4，如表4所示：

Table 4 PA Indexes表4 PA指標

4) 低秩近似(low-rank approximation, LAR)

低秩近似方法的目的是尋找一個低秩矩陣用來近似原始的矩陣.在鏈路預測中，低秩近似方法通過計算得到一個秩為k的最優低秩矩陣Ak用來近似原始的網絡鄰接矩陣A.進行鏈路預測時，將矩陣Ak中的第i行和第j列對應位置取值作為節點對i,j間鏈路的打分.文獻[12]采用了奇異值分解SVD方法對原始網絡矩陣進行低秩近似表示.本文實驗中不僅采用了SVD方法，同時也采用了非負矩陣分解方法NNMF，將2種基于低秩近似表示的鏈路預測方法分別記為：LAR-SVD和LAR-NNMF.

4.4 實驗結果及分析

實驗中經過反復測試發現，參數分別進行設置時結果最優：

Twitter 1中，L=80，Sthr=0.9，λS=0.8,

Twitter 2中，L=40，Sthr=0.97，λS=0.6,

Weibo 1中，L=80，Sthr=0.9，λS=1.6,

Weibo 2中，L=60，Sthr=0.9，λS=0.6.

除上述參數外，模型中的正則化參數設置為λU=λW=0.05.以下實驗中若非特別說明，上述參數均為最優結果時的參數.

4.4.1 基線方法比較

表5為本文方法FPMF與基線方法BPMF和TS在4組數據集中的比較結果.

Table 5 Comparison of Baseline Methods表5 基線方法比較(AUC±std)

從表5中可以看出FPMF方法在4組數據集中比2個基線方法獲得了更好的AUC結果.2種基線方法BPMF和TS分別是基于用戶網絡結構和主題相似信息進行鏈路預測，而FPMF是將2種信息融合在統一的概率產生式框架下進行鏈路預測.實驗中融合后的方法能夠優于融合前的2種方法，驗證了本文融合概率矩陣分解的有效性.

4.4.2 與已有方法比較

圖5與圖6分別顯示了本文方法與已有4類共11種常見鏈路預測方法比較的AUC和Accuracy結果.從圖5,6中可看到，FPMF方法在4組數據集中大多數情況下獲得了最好的Accuracy和AUC，并在不同的數據集中FPMF方法能夠獲得較為穩定的結果.比較方法中，基于公共鄰居的4種方法(CN1，CN2，CN3，CN4)在2組Weibo數據集上的表現都要差于2組Twitter數據集，說明其預測能力的不穩定.在基于偏好指標的方法(PA1，PA2，PA3，PA4)中，PA1與PA2表現較好，且能夠獲得相比公共鄰居更好的AUC結果，同時在2類數據集中保持了較好的穩定性，但就Accuracy結果而言明顯低于本文FPMF方法.同偏好指標類似，基于Katz的方法能夠獲得相對不錯的AUC結果，但Accuracy結果也明顯低于本文方法.這說明在鏈路預測排序精度方面，本文FPMF方法能夠獲得更好的鏈路排序結果.

Fig. 5 Accuracy results of comparison methods圖5 比較方法的Accuracy結果

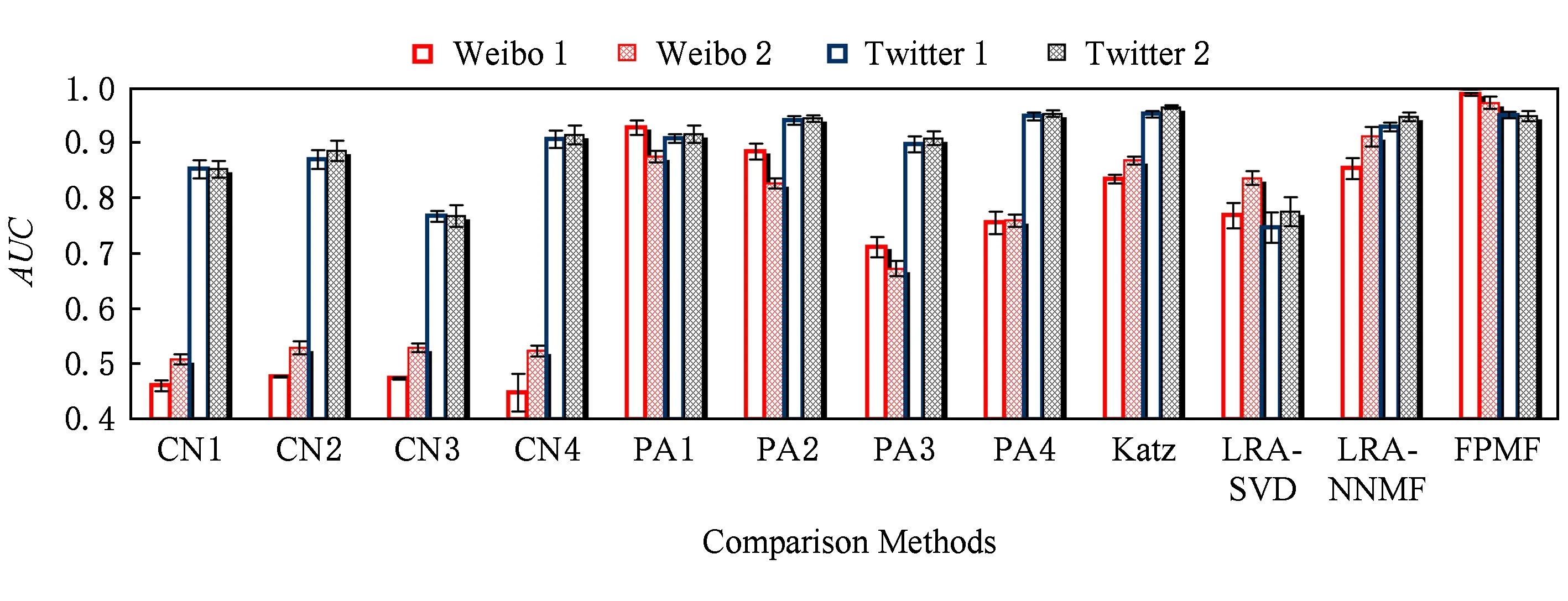
Fig. 6 AUC results of comparison methods圖6 比較方法的AUC結果

相比基于公共鄰居、偏好性和Katz方法，基于低秩近似的方法(LAR-SVD，LAR-NNMF)在不同數據集中獲得了更穩定的AUC和Accuracy結果，但這2種方法仍然低于本文FPMF方法.總的來說，本文方法既繼承了低秩近似方法的穩定性，同時由于融合了社交信息網絡中拓撲和非拓撲2方面信息，使得該方法與已有鏈路預測方法相比有明顯提升.

4.4.3 稀疏參數Sthr分析

本文FPMF方法中，參數Sthr用來控制用戶主題相似網絡S的稀疏化程度，Sthr取值越大主題相似網絡越稀疏.圖7顯示了稀疏化參數Sthr的不同取值在4組數據集中對鏈路預測結果和算法性能的影響.每個圖中橫軸代表稀疏化參數Sthr的取值(從0.1～0.99)，2個縱軸分別代表模型算法迭代1 000次所花費的時間和鏈路預測的AUC結果.從圖7(a)～(d)中時間曲線可以看出，隨著稀疏化參數Sthr取值變大，模型算法迭代所花費的時間會明顯減小.這說明用戶主題相似網絡越稀疏，算法運行所需時間越少.觀察圖7(a)～(d)中的AUC曲線，可以發現隨著稀疏化參數Sthr取值增大，鏈路預測AUC的結果也在提高，而當稀疏化參數Sthr達到一定閾值時預測結果將會停止提高甚至減小.以上現象說明用戶主題相似網絡的稀疏化程度在一定程度影響最終鏈路預測的結果與性能，合理選擇Sthr取值能夠有效提升鏈路預測結果.分析其原因，我們認為當Sthr取值很大時，用戶主題相似網絡會十分稀疏，FPMF模型中只能考慮少量的用戶對之間具有很高主題相似度的信息，而當Sthr取值很小時，模型中將會考慮大量用戶對之間的主題相似度信息，從而增加噪聲，一定程度影響鏈路預測結果.

Fig. 7 Analysis of the sparse parameters圖7 稀疏化參數分析

4.4.4 參數λS分析

λS參數是平衡FPMF模型中用戶關注被關注網絡和主題相似網絡2種信息的.如果模型中λS=0，等同于只考慮用戶間關注網絡的信息(如基線中的BPMF方法)；如果λS取無窮大，模型只考慮用戶間主題相似網絡的信息.

圖8(a)～(d)顯示了該模型在4組數據集中隨著λS參數取值變化時AUC結果的變化.可以看到隨著λS參數取值增大，AUC結果開始提升;當λS參數增加到一定閾值時，AUC結果會停止提升甚至開始下降.這說明在模型中應選擇適中的λS參數來平衡用戶關注被關注網絡和用戶主題相似網絡2種信息.

Fig. 8 Analysis of the weight parameters圖8 權重參數分析

5 結論與展望