支持訪問更新的可驗證外包屬性加密方案1

林素青

（天津財經大學理工學院，天津 300222）

1 引言

隨著云計算的發展，越來越多的用戶將自己的數據存儲至云端，便于隨時隨地下載和共享。為確保公共云存儲數據的私密性，用戶需要事先把數據加密成密文狀態再上傳至云端，而為實現一對多的密態數據共享模式，可借助屬性加密(ABE)[1]的方法對數據進行加密。屬性加密根據訪問策略和屬性集合是否匹配確定解密訪問的權限，若訪問策略與密鑰相關聯，則稱為基于密鑰策略的屬性加密(KP-ABE)[2-3]；若訪問策略與密文相關聯，則稱為基于密文策略的屬性加密(CP-ABE)[4]。傳統的屬性加密方案的解密計算量往往會隨著訪問結構的復雜程度而呈線性增長的趨勢，終端解密的計算負荷較重，為減輕終端用戶的計算負擔，可構造具有外包解密功能的屬性加密方案(OABE)[5]，將絕大部分解密計算量外包給第三服務器執行，在不改變密文訪問權限的前提下簡化密文形式，使終端用戶只需利用極少的計算量即可完成解密過程，從而滿足計算能力有限的弱終端用戶的訪問需求。若第三方服務提供商是不可信任的，即可能存在惡意行為，或服務器因故不能誠實可靠地執行外包解密算法，而向用戶反饋錯誤的計算結果，則需要通過算法設計實現對外包計算的正確性檢驗，構造具有外包解密可驗證功能的屬性加密方案(VO-ABE)[6-9]。若密文的訪問權限需要變更以使某些特定的原未授權用戶及時獲取數據，則可由已授權用戶借助外包服務器更新與密文相關聯的訪問策略或屬性集合，重新定義授權訪問用戶群體，構造支持訪問更新的外包屬性加密方案(AU-OABE)。

目前，關于支持訪問更新的外包屬性加密方案(AU-OABE)的同類研究工作很多，但方案所具有的功能、安全性和實現效率等方面均有待提高。2009年，Liang等[10]考慮用代理重加密方法實現密文訪問權限的更新，首次提出密文策略的屬性基代理重加密方案，但該方案不支持線性秘密共享方案(LSSS)表達的訪問結構，推廣應用有一定的局限性。Luo等[11]提出具有重加密可控制性質的CP-AB-PRE方案，但解密過程仍然包含雙線性對運算，很難滿足弱終端用戶的訪問需求。2014年，Liang等[12]構造了支持 LSSS訪問結構的屬性基代理重加密方案。隨后，又提出兼顧密文搜索、密態數據共享，以及用戶搜索和訪問權限更新的屬性加密方法，但方案的設計非常復雜，實用性不強。2015年，Shao等[13]提出在線-離線的CP-AB-PRE方案，支持LSSS訪問結構，實現密文訪問策略的代理更新，并證明方案具有選擇IND-CPA安全性，但該方案建立在代理服務器是半可信任的前提假設下，且未考慮密鑰的安全性。

本文提出支持訪問更新的可驗證外包屬性加密方案(AU-VOABE)，以基于密鑰策略的屬性加密方案[3]為基礎，借助不可信任的第三方服務器，實現密文訪問權限的更新和外包解密等計算，并通過算法設計，實現對外包計算結果的正確性檢驗，確保第三方服務器能誠實可靠地執行算法過程，構造支持 LSSS訪問結構的AU-VOABE方案，全面考慮方案的明文數據和解密密鑰可能遭遇的威脅和攻擊，構建關于原始密文和更新密文的安全模型、關于用戶解密密鑰的安全模型，以及外包計算的驗證可靠性模型，在標準模型下證明方案具有選擇IND-CPA安全性、私鑰安全性和驗證可靠性。與文獻同類方案相比，本文方案能兼顧功能的增加、安全性的保持和實現效率的優化。

2 預備知識

2.1 符號說明

記N為自然數集，R為實數集。1λ(λ∈N)表示λ個1形成的字符串，λ為安全參數。b∈RS表示從屬性集合S中均勻隨機選取元素b。1G表示群G的單位元。p(p∈Θ (2λ))記為素數，Zp由模p剩余類全體{0,1,…,p-1}構成，表示Zp{0}。

2.2 雙線性映射與困難問題假設

定義1（雙線性映射） 設和分別表示素數p階乘法循環群，稱為雙線性映射，如果其滿足如下條件。

2) 非退化性：若g為群G的生成元，則e(g,g) ≠1GT。

稱G為素數p階雙線性群，若存在群GT和雙線性映射e，使上述性質成立。

下面描述判定q-BDHE假設和計算q-BDHE假設。

定義2（判定q-BDHE假設） 設分別表示素數p階乘法群，g為群的生成元，表示雙線性映射。對于任意概率多項式時間 (PPT) 算法A，存在可忽略函數negl滿足

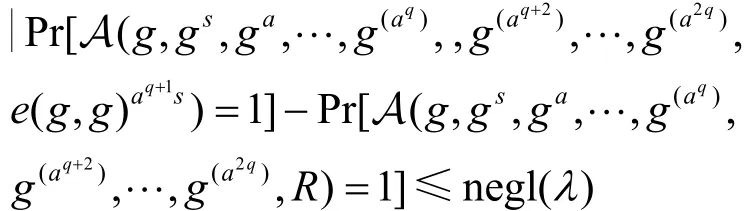
定義3(計算q-BDHE假設) 對于任意概率多項式時間 (PPT) 算法A，存在可忽略函數negl滿足

2.3 系統模型

為滿足弱終端用戶訪問權限可更新的應用需求，本文借助外包服務器實現屬性基密態數據的訪問權限更新和高效安全的終端解密訪問。此處假設外包服務器是不可信任的，即它有偷窺私密信息的好奇心且可能不會誠實地執行外包計算過程并返回錯誤的計算結果。為確保外包服務器能誠實可靠地執行相關操作，本文將對訪問權限更新和外包解密過程同時進行計算的正確性檢驗。系統模型如圖1所示。

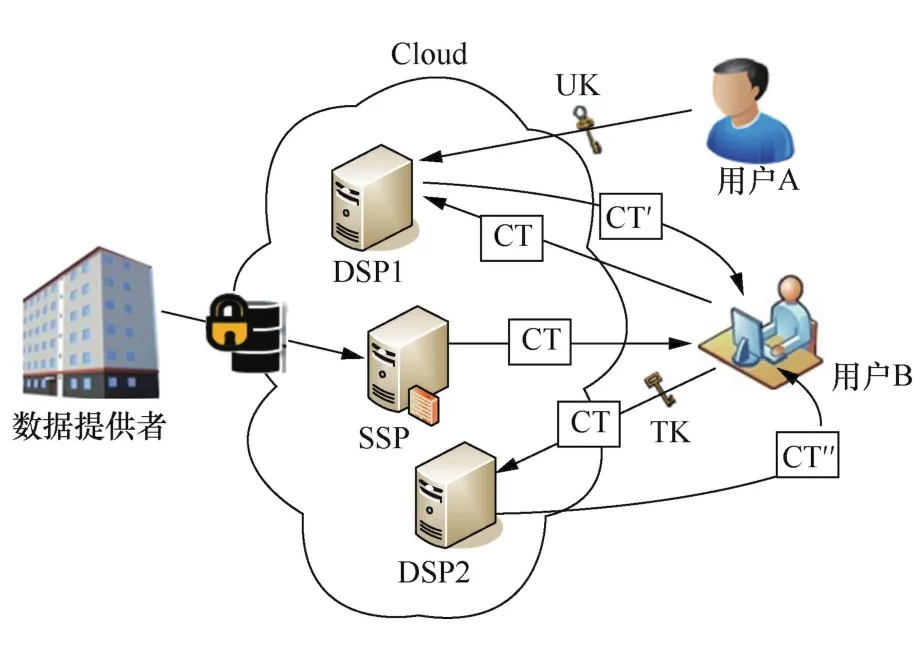
圖1 系統模型

系統模型中有3個服務器SSP、DSP1、DSP2。服務器SSP存儲所有屬性基密態數據，DSP1和DSP2為外包服務器，分別用于更新密態數據的訪問權限和執行外包解密算法。

如圖 1所示，數據提供者將共享數據通過基于屬性的加密方法加密得到密態數據，并上傳至存儲服務器SSP。假設用戶A對于存儲在SSP中的密態數據具有解密訪問的權限，而用戶B可下載密文卻不具有解密訪問的權限。考慮緊急需求時已授權用戶均不在場的情形，需通過變更訪問權限，使在場的未授權用戶及時獲取解密訪問權限。借助外包服務器，已授權用戶A可根據用戶B的屬性特征更新密態數據相關聯的屬性集合，使用戶B獲得解密訪問的權限。具體過程描述如下。

服務器DSP1收到用戶A提供的更新密鑰和用戶B提供的密文，執行特定的算法更新密文相關聯的屬性集合并將所得新密文返回給用戶B。若用戶B希望將解密的部分計算外包給服務器執行，可生成外包解密密鑰，并將其和密文一起發送給服務器DSP2，DSP2執行外包解密算法將密文轉化為簡化形式并發給用戶B。最終用戶B只需很少的計算量并可恢復出原始明文消息，同時用戶B可通過算法驗證服務器DSP1和DSP2執行外包計算的真實可靠性。

2.4 AU-VOABE的算法描述

設A和S分別表示訪問結構和屬性集合，本文構造AU-VOABE方案，算法描述如下。

1)Setup(1λ,U)：系統建立算法。輸入安全參數λ和屬性空間U，輸出公共參數PP和主私鑰MSK。

3)Enc(PP,M,S)：加密算法。輸入公共參數PP、消息M，以及屬性集合S，輸出密文CTS。

4)De c(SKA,CTS)：解密算法。輸入訪問結構A對應的密鑰SKA，屬性集合S對應的密文若S滿足輸出明文M；否則，輸出錯誤標識符⊥。

5)UP.KGen(PP,SKA,S′)：更新密鑰生成算法。輸入公共參數PP、訪問結構A對應的密鑰SKA、屬性集合S′，輸出更新密鑰UKA→S′。

7)OT.KGen(PP,SKA′)：外包解密密鑰生成算法。輸入公共參數PP、訪問結構 A′對應的密鑰SKA′，輸出外包解密密鑰TKA′和相應的數據恢復密鑰RKA′。

正確性：AU-VOABE方案是正確的，當且僅當對于任意正確產生的公共參數PP和主私鑰MSK，任意的屬性集合S、訪問結構A，以及消息M，若S滿足A，則有以下等式成立。

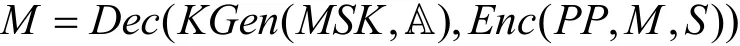
并且，對于任意正確生成的密鑰SKA、SKA′、更新密鑰UKA→S′、外包解密密鑰TKA′和數據恢復密鑰RKA′，若S滿足A且S′滿足 A′，則有以下等式成立。

2.5 AU-VOABE的模型

假設存儲服務器SSP是半可信任的，即SSP誠實地執行協議算法，但同時也會盡可能多地偷窺私密信息，SSP中存儲的密文供全體用戶下載。假設DSP1和DSP2均為不可信任的外包服務器，可能不會誠實地執行算法，并輸出錯誤的計算結果。本文考慮5種類型的敵手。

第1類敵手：被敵手拉攏的部分用戶與DSP1服務器提供商合謀，從服務器DSP1中獲取更新密鑰，用他們擁有的解密密鑰，試圖從密文中獲取其他用戶的私密信息。

第2類敵手：被敵手拉攏的部分用戶與DSP1服務器提供商合謀，用他們擁有的解密密鑰，試圖從更新密文中獲取其他用戶的私密信息。

第3類敵手：被敵手拉攏的部分用戶與DSP2服務器提供商合謀，從服務器DSP2中獲取外包解密密鑰，并用他們擁有的解密密鑰，試圖從密文中獲取其他用戶的私密信息。

第4類敵手：被敵手拉攏的部分用戶與DSP1服務器提供商合謀，從服務器DSP1中獲取更新密鑰，并用他們擁有的解密密鑰，試圖獲取其他用戶的解密密鑰。

第5類敵手：DSP1和DSP2服務器提供商，與部分用戶合謀，分別獲取更新密鑰和外包密鑰，以及部分解密密鑰，試圖通過外包計算的可靠性驗證。

第1、2、3類敵手攻擊方案的數據安全性，第4類敵手攻擊方案的密鑰安全性，第5類敵手攻擊方案外包計算的驗證可靠性。下面針對5種類型的敵手，分別定義 AU-VOABE方案關于密文和更新密文的IND-CPA安全性，以及私鑰安全性和外包計算的驗證可靠性。為刻畫方案針對5類敵手的安全性，本文分別描述任意PPT敵手A與挑戰者之間的游戲如下。

針對第1類敵手的數據安全性

1)Init：初始化階段。敵手A輸出挑戰的屬性集合S?。

2)Setup：系統建立階段。挑戰者調用算法Setup(1λ,U)得到公共參數PP和主私鑰MSK，并將公共參數PP發送給敵手A。

3)Phase1：第1次詢問階段。挑戰者初始化一個空表格T和空集合D。敵手A提交下列詢問。

① 解密密鑰詢問：給定與屬性集合S?不匹配的訪問結構A，挑戰者調用算法KGen(MSK,A)輸出SKA，并令

②更新密鑰詢問：給定與S?不匹配的訪問結構和屬性集合S′，若已經存在表格T中，則挑戰者輸出UKA→S′；否則，挑戰者調用算法KGen(MSK,A )→SKA和UP.KGen(PP,SKA,S′) →UKA→S′，并將(A,S′,SKA,UKA→S′)存入表格T中，輸出UKA→S′。

4)Challenge：敵手A提交兩個等長的消息M0,M1，挑戰者均勻隨機選取b∈{0,1}，調用加密算法Enc(PP,Mb,S*)，得到挑戰密文CT*。

5)Phase2：第2次詢問階段。敵手A繼續提交解密密鑰和更新密鑰的詢問，要求密鑰對應的訪問結構A與給定的屬性集合S?不匹配，挑戰者給出相應的回復。

6)Guess：猜測階段。敵手A輸出對b的猜測b′∈ {0,1}。若b′=b，敵手贏得游戲。

針對第2類敵手的數據安全性

除了挑戰階段，與第1類敵手的數據安全性描述基本相同，描述如下。

1)Challenge：敵手A提交兩個等長的消息M0,M1，挑戰者選取訪問結構A和與之匹配的屬性集合S，調用算法和得到更新密鑰隨后，均勻隨機選取b∈{0,1}，調用算法得到挑戰密文

針對第3類敵手的數據安全性

除了第1次詢問與第1類敵手的數據安全性描述基本相同，描述如下。

Phase1：第1次詢問階段。挑戰者初始化一個空表格T和空集合D。敵手A提交下列詢問。

① 解密密鑰詢問：給定與屬性集合S?不匹配的訪問結構A，挑戰者調用算法KGen(MSK,A)輸出SKA，并令

定義3AU-VOABE方案關于第i(i∈ {1 ,2,3})類敵手具有選擇 IND-CPA安全性，如果任意的PPT敵手A在上述游戲中的優勢是可忽略的，即

為避免平凡攻擊，本文引入關于兩個訪問結構的緊性定義。

定義4設A和 A′是兩個由正屬性構成的單調訪問結構，將A表示為析取范式A1∨…∨Ak。如果存在 Ai(i∈[k])，滿足：對于任意集合S，若S滿足Ai，則必有S滿足 A′，就稱 A′次緊于A。

針對第4類敵手的密鑰安全性

1)Init：初始化階段。敵手A輸出挑戰的訪問結構 A?。

2)Setup：系統建立階段。挑戰者調用算法Setup(1λ,U)得到公共參數PP和主私鑰MSK，并將公共參數PP發送給敵手A。

3)Phase1：第1次詢問階段。挑戰者初始化一個空表格T和空集合D。敵手A提交下列詢問。

① 解密密鑰詢問：給定訪問結構A（A次緊于 A?不成立），挑戰者調用算法KGen(MSK,A)輸出SKA，并令D：=D∪{A}。

② 更新密鑰詢問：給定訪問結構A和屬性集合S′，若(A,S′,SKA,UKA→S′)已經存在表格T中，則挑戰者輸出更新密鑰UKA→S′；否則，挑戰者調用算法KGen(MSK,A )→SKA和UP.KGen(PP,SKA,S′) →UKA→S′，并將(A,S′,SKA,UKA→S′)存入表格T中，輸出UKA→S′。

4)Output：敵手A輸出訪問結構 A?相關聯的解密密鑰SK?。對于任意一個與 A?匹配的屬性集合S，調用算法Enc(PP,M,S) →CTS，若總有Dec(SK?,CTS)→M成立，則稱敵手贏得游戲。

定義5AU-VOABE方案關于第4類敵手具有選擇弱主私鑰安全性，如果任意的PPT敵手A贏得上述游戲的優勢是可忽略的，即Pr[Awins] ≤ negl(λ)。

針對第5類敵手的驗證可靠性

1)Setup：系統建立階段。挑戰者調用算法Setup(1λ,U)得到公共參數PP和主私鑰MSK，并將公共參數PP發送給敵手A。

2)Phase1：第1次詢問階段。挑戰者初始化空表格T1、T2和空集合D。敵手A提交下列詢問。

① 解密密鑰詢問：給定訪問結構A，挑戰者調用算法KGen(MSK,A)輸出SKA，并令

② 更新密鑰詢問：給定訪問結構A和屬性集合S′，若(A,S′,SKA,UKA→S′)已經存在表格T1中，則挑戰者輸出更新密鑰UKA→S′；否則，挑戰者調用算法KGen(MSK,A )→SKA和UP.KGen(PP,SKA,S′) →UKA→S′，并將(A,S′,SKA,UKA→S′)存入表格T1中，輸出UKA→S′。

③ 外包密鑰詢問：給定訪問結構A，若(A,SKA,TKA,RKA)已經存在表格T2中，則挑戰者輸出外包密鑰TKA；否則，挑戰者調用算法KGen(MSK,A )→SKA和OT.KGen(PP,SKA)→(TKA,RKA)，并將(A,SKA,TKA,RKA)存入表格T2中，輸出TKA。

④ 驗證解密詢問：給定訪問結構 A′、原始密文CTS、更新密文UTS′和外包解密密文CIS′，若(A ′ ,SKA′,TKA′,RKA′)已經存在表格T2中，挑戰者調用算法VF.Dec(PP,RKA′,CTS,UTS′, C IS′)，并輸出結果；否則，輸出錯誤標識符⊥。

3)Challenge：敵手A提交消息M?和屬性集合S。挑戰者調用Enc(PP,M*,S)生成密文CTS并將其返回給敵手A。

4)Phase2：第2次詢問階段。敵手A繼續提交解密密鑰、更新密鑰、外包密鑰和驗證解密等詢問。

5)Output：敵手A輸出以及與相匹配的訪問結構A?。若則稱敵手A贏得游戲。不妨假設已經存在表格T2中。

定義6AU-VOABE方案關于第5類敵手具有驗證可靠性，如果任意的PPT敵手A贏得上述游戲的優勢是可忽略的，即Pr[Awins] ≤ negl(λ)。

3 AU-VOABE方案

結合密鑰盲化方法[5]和可驗證外包解密技術[7]，本文構造支持可驗證訪問更新的外包屬性加密方案(AU-VOABE)，具體算法描述如下。

3.1 方案的構造

通過改進文獻[3]的 KP-ABE方案，得到AB-KEM基礎方案，是AU-VOABE方案的基本組塊。方案算法描述如下。

1)KM.Setup(1λ,U)：選取一個素數p(p∈階雙線性群系統表示從群至群的雙線性映射。設g為群的一個生成元。隨機選取定義算法輸出公共參數PK=和主私鑰

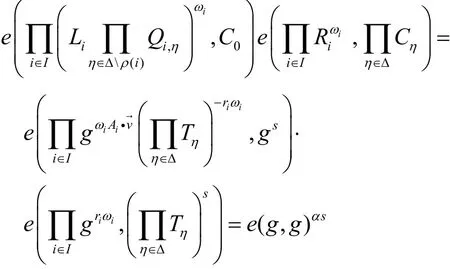
若判定|U|-BDHE假設[3]成立，類似于文獻[3]定理1的證明方法，易證上述AB-KEM方案具有選擇IND-CPA安全性。以上述方案為基礎，引入Pedersen承諾方案，構造訪問更新可驗證的外包屬性加密(AU-VOABE)。算法描述如下。

1)Setup(1λ,U)：設U= {1,2,… ,n}為屬性空間。選取一個素數p階雙線性群系統(G,GT,e)，表示從群至群的雙線性映射。設g為群G的一個生成元，表示抗碰撞Hash函數，F：GT→{0,1}?表示輸出長度足夠長的偽隨機數生成器。隨機選取x,α,算法輸出公共參數PP=(g,h,和主私鑰

3)Enc(PP,S,M)：隨機選取設輸出密文

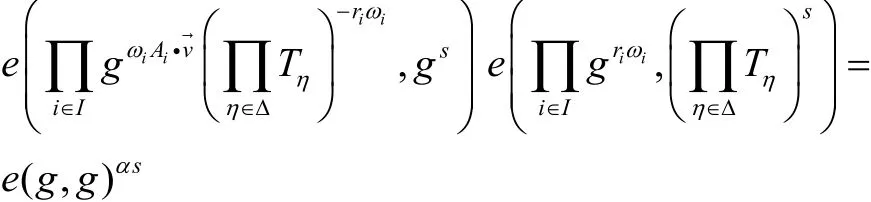
并令F(e(g,g)αs) =DK||d。若計算并輸出M。

5)UP.KGen(PP,SKA,S′)： 設選取更新密鑰因子δ∈ {0,1}?和輔助的密鑰盲化因子并令隨機選取并令計算令輸出更新密鑰

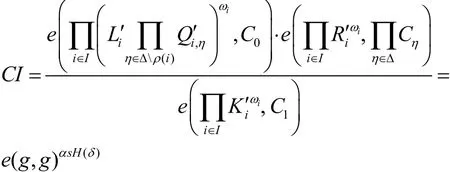
7)OT.KGen(PP,SKA)：設選取外包密鑰盲化因子并設輸出外包解密密鑰和相應的恢復密鑰RKA=ξ。

8)OT.Dec(TKA,CS′)： 設若屬性集合S′滿足訪問結構A，則存在使設計算

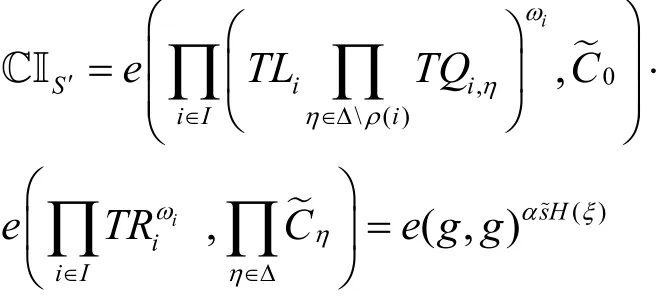
3.2 安全性分析

定理 1 若判定|U|-BDHE假設[3]成立，則AU-VOABE方案關于第i類敵手具有選擇IND-CPA安全性(i= 1,2,3)。

證明 首先證明 AU-VOABE方案對于所有第1類敵手具有選擇IND-CPA安全性。考慮挑戰者與敵手之間的兩類游戲。

Game0：方案對第1類敵手的選擇IND-CPA安全性游戲。挑戰密文其中，通過計算得到。

Game1：F(DK0) =DK||d，DK0是從會話密鑰空間中均勻隨機選取的，其余過程與Game0相同。

Game2：中的DK均勻隨機選取自{0,1}|Mb|，且中的d是一個隨機的字符串，其余過程與Game1相同。

Game3：其余過程與Game2相同。

Game4：其中隨機選取自明文空間，其余過程與Game3相同。

下面分別證明Game0與Game1、Game1與Game2、Game2與Game3、Game3與Game4之間的不可區分性。

假設敵手A1能以不可忽略的優勢區分Game0與Game1，則可構造算法B以不可忽略的優勢攻破基礎方案的選擇IND-CPA安全性。

1)Init：初始化階段。敵手A1發布挑戰的屬性集合S?，B將S?轉給挑戰者。

2)Setup：系統建立階段。挑戰者將公開參數發送給B。B隨機選取u1,u2∈RG，抗碰撞Hash函數和輸出長度足夠長的偽隨機函數F，并將公開參數發送給敵手A1。

3)Phase1：第1個詢問階段。

① 解密密鑰詢問：敵手A1向B提交對應于訪問結構A的解密密鑰詢問，其中屬性集合S?不滿足訪問結構A。B向挑戰者提交同樣的密鑰詢問，并將收到的密鑰SKA轉發給敵手A1。

② 更新密鑰詢問：敵手A1提交對應于訪問結構A和屬性集合S′的更新密鑰詢問。若S?不滿足訪問結構A，則B向挑戰者提交對應于訪問結構的解密密鑰詢問，收到密鑰調用算法得到更新密鑰若S?滿足訪問結構A，則B選取設定并將發送給敵手

4)Challenge：挑戰階段。敵手A1提交兩個等長的明文消息M0,M1給B，B將M0,M1轉交給挑戰者。挑戰者調用基礎方案的加密算法得到然后均勻隨機選取β∈ {0,1}。若β=0，令若β=1，DR0為會話密鑰空間中均勻隨機選取的密鑰。挑戰者將發送給B。B計算隨機選取b∈R{0,1}，設定并將挑戰密文發送給敵手A1。

5)Phase2：第2個詢問階段。與第1個詢問階段Phase1相同，敵手A1提交解密密鑰詢問和更新密鑰詢問，B分別按照Phase1中①和②的步驟，給出相應的回復。

6)Guess：猜測階段。敵手A1輸出b′∈ {0,1}。若b′=b，B輸出β′=0；否則，B輸出β′=1。

易見，若β=0，B恰好模擬了Game0的實驗環境；若β=1，B恰好模擬了Game1的實驗環境。因此，若敵手A1能以不可忽略的優勢區分Game0與Game1，則B能以不可忽略的優勢攻破AB-KEM基礎方案的選擇IND-CPA安全性。

由偽隨機生成器F和抗碰撞 Hash函數H的性質，可得到Game1中的DK,d,H(DK),H(d)均與隨機字符串不可區分。因此，Game1與Game2不可區分。同時，由 Pedersen承諾方案的計算隱藏性和一次一密的安全性分別可得Game2與Game3、Game3與Game4之間的不可區分性。于是，Game0與Game4不可區分，而Game4中的挑戰密文不包含敵手A1提供的M0,M1的任何信息，所以，敵手A1在Game4中的優勢是可忽略的，從而，敵手A1在Game0中的優勢是可忽略的。方案針對第 1類敵手的選擇IND-CPA安全性證明完畢。

針對第 2類敵手A2，挑戰密文CI?=(CI,這里CI=e(g,g)αsH(δ)，其中類似于針對第1類敵手的安全性分析，可證明得到的選擇IND-CPA安全性。于是，與隨機的會話密鑰不可區分。基于一次一密的安全性和Pedersen承諾方案的計算隱藏性，可獲得針對第2類敵手的選擇IND-CPA安全性。

將對第 1類敵手的安全性證明中的更新密鑰詢問改成外包密鑰詢問，并將密鑰盲化因子δ加密得到的密文作為挑戰密文的一部分，可類似實現對第3類敵手的安全性證明。

綜上，完成定理2的證明。

下面討論AU-VOABE方案的密鑰安全性。

定理 3若計算|U|-BDHE假設成立，則AU-VOABE方案具有選擇弱主私鑰安全性。

證明假設存在PPT敵手A能以不可忽略的優勢攻破方案的選擇弱主私鑰安全性，則可以構造算法B，以不可忽略的優勢解決計算|U|-BDHE問題。

1) Init：初始化階段。敵手A發布要挑戰的訪問結構

3) Query Phase：詢問階段。敵手A提交如下詢問

4) Output：輸出階段。敵手A以不可忽略的概率輸出一個合法的解密密鑰。

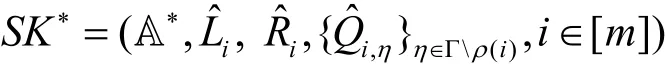
根據方案的定義

于是

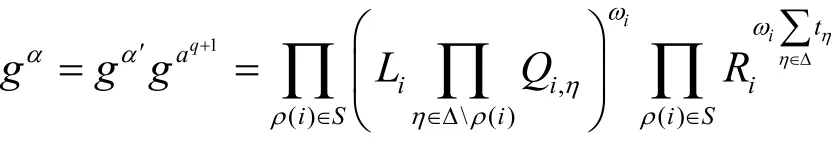
定理4若離散對數假設成立，則AU-VOABE方案具有外包可驗證性。

證明假設第5類敵手A能以不可忽略的優勢攻破方案的可驗證性，則可構造算法B求解離散對數問題。

1)Setup：系統建立階段。B選取一個素數階雙線性群系統表示從群至群的雙線性映射，g為群G的一個生成元，隨機選取x,α,定義并選取抗碰撞Hash函數和輸出長度足夠長的偽隨機函數F，將公共參數H,F)發送給敵手A。

2)Phase1：第 1個詢問階段。敵手A分別提交解密密鑰詢問、更新密鑰詢問、外包密鑰詢問、可驗證解密詢問，B利用主私鑰構造相應密鑰并回復。

3)Challenge：挑戰階段。敵手A提交明文消息M?和屬性集合S。B調用算法Enc(PP,并將密文輸出給敵手A，其中

4)Phase2：第2個詢問階段。與第1個詢問階段Phase1相同，敵手A提交解密密鑰詢問，更新密鑰詢問，外包密鑰詢問，可驗證解密詢問，B按照Phase1的步驟，給出相應的回復。

5)Output：輸出階段。敵手A輸出和S?滿足的訪問結 構 A?，其中

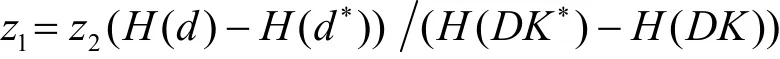
說明B成功解決離散對數問題，與離散對數假設矛盾，所以，AU-VOABE方案具有外包可驗證性。

4 方案的對比分析

本文將構造的 AU-VOABE方案與文獻[5,7,10,12]中同類方案進行比較，分別從效率、安全性和功能等方面進行分析，主要關注終端用戶的解密計算量和數據安全性，以及訪問權限是否可變更，解密計算是否可外包和外包計算是否可驗證等功能。

如表1所示，本文方案相比同類方案，功能更加全面，且為確保訪問權限更新和外包解密算法均能誠實可靠地被執行，本文通過算法設計增加了方案在外包計算上的可驗證功能，包括對訪問權限更新算法的驗證和對外包解密計算結果的正確性檢驗。在功能增加的同時，方案依然保持與同類方案相同的安全性。

如表 2所示，本文通過統計用戶執行加密和更新密鑰生成算法，服務器執行密文更新算法、外包密鑰生成算法和外包解密算法，以及終端用戶執行最后的驗證解密算法等所需的計算量，將本文方案與同類方案的實現效率進行細致的對比。文獻[5,7]方案均不具有訪問權限更新的功能，本文方案的外包密鑰生成和外包解密計算量與文獻[7]相同，加密和解密計算量比文獻[7]方案分別僅增加一次模指數運算。文獻[10, 12]方案均不具有外包解密的功能，本文方案的加密計算量比文獻[12]方案少兩次模指數運算，文獻[12]的解密計算量包含 8次雙線性對運算，且模指數運算次數隨屬性個數的增加而呈線性增長的趨勢，而本文方案的終端解密計算不含雙線性對運算，且僅包含4次模指數運算，計算能力有限的弱終端用戶也可有效訪問。

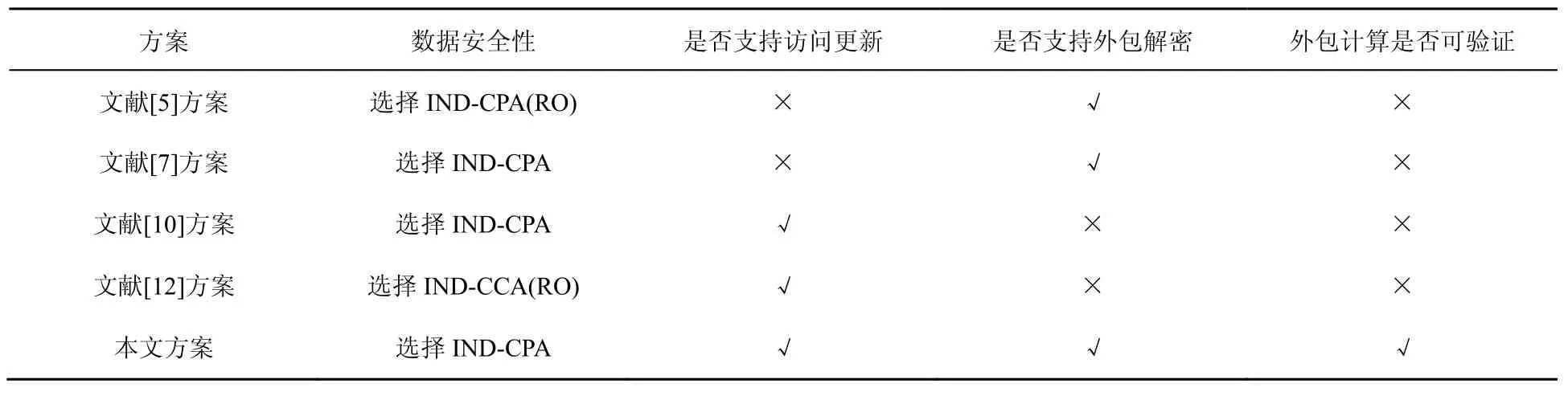
表1 安全性和功能對比

表2 計算量對比

5 結束語

本文全面考慮方案所需實現的功能和可能遇到的數據安全性和密鑰安全性問題，為滿足計算能力有限的弱終端用戶的訪問需求，終端訪問的原密文和更新密文均可進行外包簡化計算。由于

外包服務提供商是完全不可信任的，外包服務提供商可能會存在惡意行為，或外包服務器可能因故不能誠實可靠地執行算法過程，而向用戶反饋錯誤的結果，這將導致終端用戶解密得到錯誤的消息。為避免因外包服務器的錯誤反饋而導致的終端解密結果出錯，本文通過算法設計增加了方案在外包計算上的可驗證功能，包括對訪問權限更新算法的驗證和對外包解密計算結果的正確性檢驗。