舷間液艙模型聲振耦合特性及聲輻射控制
王世彥,俞孟薩
(中國船舶科學(xué)研究中心,江蘇 無錫 214082)
0 引 言
機械噪聲是水下航行體低航速工況的主要噪聲源。隨著機械噪聲控制的要求不斷提高,除了在艇內(nèi)提高浮筏隔振效果外,還試圖在舷間增設(shè)隔聲阻尼層,從多個層面控制機械噪聲。白振國[1]詳細研究了雙層殼體舷間結(jié)構(gòu)的聲振耦合特性及聲學(xué)覆蓋層的降噪效果。但是,我們知道水下航行器航行時,需要調(diào)整其內(nèi)部舷間液艙的艙位以調(diào)節(jié)浮力大小,實現(xiàn)航行器的上浮及下潛等狀態(tài)。舷間液艙是水下航行器結(jié)構(gòu)的重要組成部分,雖然考慮了舷間聲振隔離的降噪途徑,但是沒有充分注意舷間液艙聲振耦合作用,艇內(nèi)設(shè)備產(chǎn)生的振動能量通過舷間液艙側(cè)板和艙內(nèi)水介質(zhì)兩個途徑的耦合和傳遞,在外場產(chǎn)生輻射噪聲,成為機械噪聲控制的一個短板。
水下航行體舷間液艙一般位于耐壓殼和輕外殼之間,單殼體航行體液艙則位于艇內(nèi),內(nèi)部為水介質(zhì)的雙層結(jié)構(gòu)形式。耐壓殼和輕外殼與液艙側(cè)板和水介質(zhì)相互耦合,構(gòu)成結(jié)構(gòu)與內(nèi)外聲介質(zhì)多重耦合及聲輻射的問題。針對雙層結(jié)構(gòu)的聲振耦合問題,London[2]很早就采用無限雙層平板模型用于分析隔聲量,考慮了平板結(jié)構(gòu)間空氣層共振的影響。近些年來,Antonio等[3]研究發(fā)現(xiàn)空氣層的隔聲效果隨頻率而變化,低頻段較厚的空氣層有更好的隔聲效果,而高頻段薄的空氣層則更適用。這些研究都沒有考慮平板之間連接結(jié)構(gòu)的作用,實際上連接結(jié)構(gòu)聲阻抗量級與平板聲阻抗相差不大,兩者的耦合共振對振動傳遞有很大的影響,Mohamed等[4]采用混合建模的處理方法,用有限元方法研究了雙層有限長平板與內(nèi)部聲介質(zhì)之間的聲振耦合特性。Bao和Pan[5]研究認為雙層平板結(jié)構(gòu)的噪聲傳遞控制需要考慮連接結(jié)構(gòu)。針對雙層平板構(gòu)成的矩形聲腔,Cheng等[6]采用模態(tài)法計算了聲介質(zhì)與連接結(jié)構(gòu)兩種途徑對能量傳遞的作用,明確結(jié)構(gòu)連接剛度較小、聲介質(zhì)層較薄時,聲介質(zhì)是主要能量傳遞通道,反之,則結(jié)構(gòu)通道是主要傳遞通道。陳美霞等[7]對有限長加肋和實肋板連接的雙層圓柱殼的聲輻射進行計算,討論了有限長單、雙層殼體聲輻射性能的差異,以及雙殼體間連接形式和實肋板參數(shù)變化對其聲輻射的影響。Hongisto等[8]實驗研究了不同剛度,不同數(shù)量結(jié)構(gòu)連接對有限雙層平板系統(tǒng)聲能傳遞的影響。Davy[9]用四端網(wǎng)絡(luò)法描述平板間機械連接的振動傳遞作用,數(shù)值比較了不同機械連接方式下雙層平板系統(tǒng)的聲傳遞損失。Legault和Atalla等[10-11]建立了一個正交加肋無限雙層平板模型,研究平板尺度及連接結(jié)構(gòu)對聲振傳遞特性的影響。寧少武和史治宇[12-13]考慮聲場邊界對結(jié)構(gòu)聲振耦合的影響,采用了聲波導(dǎo)模態(tài)展開求解中間聲場,結(jié)構(gòu)與聲場為弱耦合,只適用于空氣介質(zhì)的情況。張浩和劉碧龍[14]采用多層介質(zhì)傳遞矩陣模型,研究了有限雙層平板結(jié)構(gòu)敷設(shè)聲學(xué)覆蓋層在低頻段的吸聲性能。Ghosh和Bhattacharya[15]采用半解析半數(shù)值的方法,計算分析了有曲率雙層平板結(jié)構(gòu)的振動傳遞以及聲輻射規(guī)律。文獻[1]雖然考慮了舷間實肋板和水介質(zhì)與內(nèi)外殼的耦合對雙層圓柱殼聲輻射的影響,但實肋板和水介質(zhì)兩種振動傳遞途徑獨立建模,沒有考慮舷間實肋板與水介質(zhì)的相互耦合。
本文針對舷間液艙聲振耦合及聲輻射問題,采用模態(tài)法及格林公式,建立液艙結(jié)構(gòu)振動與內(nèi)外聲場的聲振耦合模型,計算在外力作用下液艙的外場輻射聲功率,數(shù)值分析液艙側(cè)板結(jié)構(gòu)及艙內(nèi)聲介質(zhì)對聲輻射的影響,并在液艙內(nèi)部敷設(shè)聲學(xué)覆蓋層,計算比較不同厚度及不同等效參數(shù)的聲學(xué)覆蓋層降低外場聲輻射的效果。結(jié)果認為液艙側(cè)板改用復(fù)合材料能夠進一步降低外場輻射聲功率。
1 計算模型
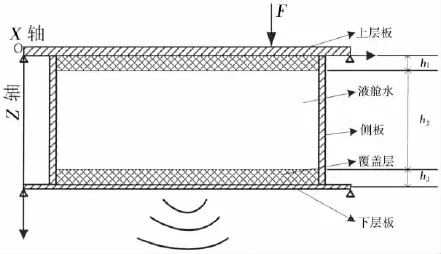
圖1 液艙結(jié)構(gòu)二維解析計算模型Fig.1 2D analytical model of a water cabin
本文針對耐壓殼和輕外殼及側(cè)板構(gòu)成的舷間液艙,考慮側(cè)板傳遞及其與液艙聲場耦合和輕外殼的外場聲輻射,建立一個由上層平板和下層平板及兩側(cè)連接側(cè)板組成的矩形聲腔模型,如圖1所示。機械激勵力沿法線方向作用在上層平板上表面,產(chǎn)生的振動一方面經(jīng)側(cè)板傳遞到下層平板,另一方面產(chǎn)生腔內(nèi)聲場并與下層平板耦合,兩種途徑引起的下層平板振動產(chǎn)生外場輻射噪聲。為了隔離聲腔聲場與平板之間的耦合,在腔內(nèi)上下平板內(nèi)側(cè)敷設(shè)聲學(xué)覆蓋層,中間部分是理想水介質(zhì),外場為半無限的理想水介質(zhì)。為簡單起見,將上下平板和聲腔考慮為二維模型,圖1中h1,h2,h3是液艙由上到下各聲學(xué)層的厚度,液艙的寬度為l0。平板的長度為l,兩側(cè)側(cè)板連接的位置分別是x1、x2。
考慮上下平板與聲腔聲場和側(cè)板面內(nèi)和面外振動的相互作用,平板耦合振動方程為:
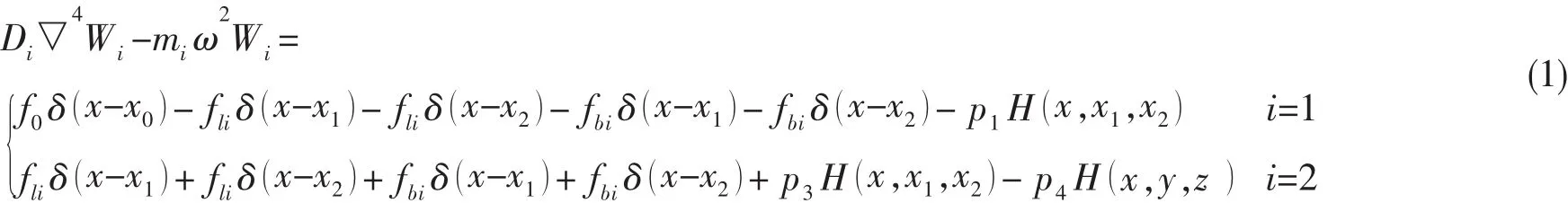
式中:Di,mi(i=1, 2 )分別為上下平板的彎曲剛度和面密度;Wi(i=1,2 )分別是上下平板彎曲振動位移;f0代表機械激勵外力,x0是激勵力作用位置;fli,fbi(i=1,2 )分為側(cè)板面內(nèi)振動和面外振動對上下平板的作用力;p1和p3是液艙聲壓對上下平板的作用,p4為外部輻射聲場對下層平板的作用。δ(x)為Dirac函數(shù),H(x,x1,x2)為矩形函數(shù)。
側(cè)板面內(nèi)和面外的振動方程[16]:

式中:ur和Wr是液艙側(cè)板面內(nèi)縱振動位移和面外彎曲振動位移,Er、Dr、υr、ρr為側(cè)板楊氏模量、彎曲剛度、泊松比和密度。
側(cè)板沿z方向?qū)ι舷缕桨宓淖饔昧梢员硎緸椋?/p>

式中:Sr為側(cè)板截面積,z3=h1+h2+h3為側(cè)板的高度。
側(cè)板與上下平板連接處滿足邊界條件:

考慮聲學(xué)覆蓋層,液艙內(nèi)部由三部分聲學(xué)介質(zhì)層組成,其中的聲場及外場聲場分別滿足波動方程:

式中:ki為波數(shù),,其中c1、c2、c3是液艙內(nèi)部各介質(zhì)層聲速,c4是外場聲介質(zhì)聲速。
液艙內(nèi)部聲場與左右側(cè)板滿足邊界條件:

式中:i=1,2,3 表示從上到下的聲學(xué)介質(zhì)層,j=1,2 表示左右側(cè)板,且z0=0,z1=h1,z2=h1+h2,z3=h1+h2+h3。
上下平板與內(nèi)側(cè)聲學(xué)覆蓋層之間滿足邊界條件:
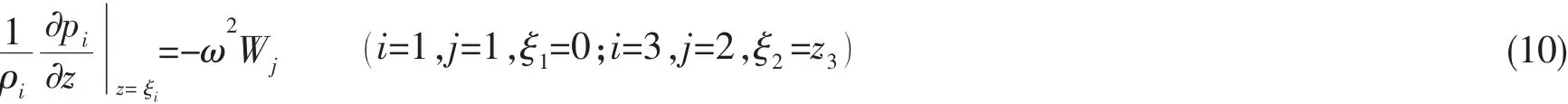
下層平板與外場聲壓滿足邊界條件:

假設(shè)上下平板為簡支邊界條件,采用模態(tài)疊加法求解(1)式,可得上下平板的振動模態(tài)方程:

其中:mim、ωim和 ηis(i=1,2 )分別為上、下平板振動的模態(tài)質(zhì)量、模態(tài)頻率及結(jié)構(gòu)損耗因子;f0m為機械外力f0對應(yīng)的廣義模態(tài)力)分別為側(cè)板面內(nèi)和面外振動對上下平板作用的廣義模態(tài)力;p1m、p3m和p4m分別為聲壓p1、p3和p4對應(yīng)的廣義模態(tài)力;(i=1,2 )為上、下平板的模態(tài)機械阻抗。
假設(shè)側(cè)板與上下平板的相互作用為點力作用,求解(2)式并利用邊界條件(5)式及上下簡支板的模態(tài)解,由(4)式可求得側(cè)板x=xj(j=1,2 )面內(nèi)振動對上、下平板 (i=1,2 )的模態(tài)作用力:
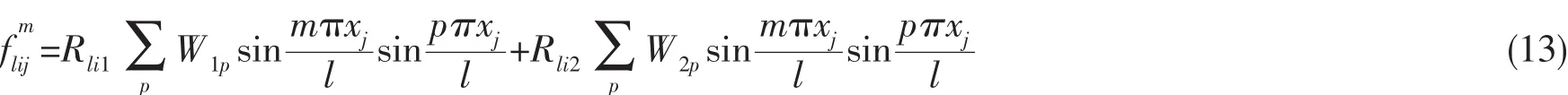
具體推導(dǎo)過程及Rlij表達式見附錄A。
側(cè)板對上下平板的作用力矩可以表示為:

采用模態(tài)法求解側(cè)板面外振動方程(3)式,并利用側(cè)板與上下平板的連接條件(6)、(7)式,得到上下平板振動位移與側(cè)板面外振動位移的關(guān)系,由(14)式可得側(cè)板對上下平板的作用力矩:
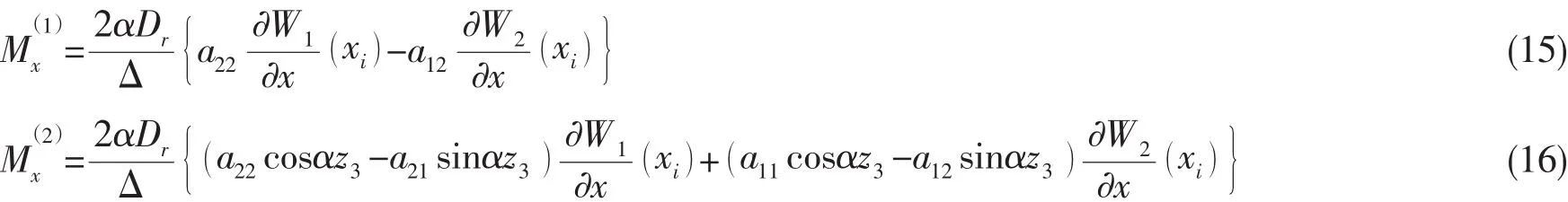
按文獻[1]的處理方法,進一步可求解得到在x=xj(j=1,2 )處側(cè)板面外振動對上下平板(i=1,2 )作用的廣義模態(tài)力:
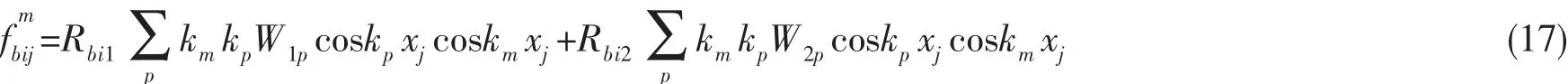
具體推導(dǎo)過程及Rbij表達式見附錄A。
液艙內(nèi)水介質(zhì)及聲學(xué)覆蓋層等三個聲學(xué)層聲壓可表示為:

假設(shè)三個聲學(xué)層之間有一層虛擬膜,其質(zhì)量和剛度為0。針對平板、側(cè)板及虛擬膜圍成的空間,采用Green公式并考慮邊界條件(9)、(10)式,可以得到各區(qū)域聲模態(tài)方程:
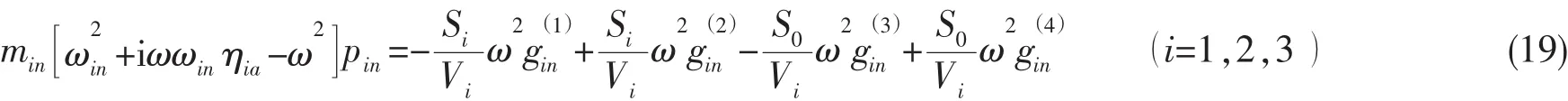
式中:min、ωin和ηia為各個聲學(xué)層的聲模態(tài)質(zhì)量、模態(tài)頻率及聲介質(zhì)損耗因子,S0是各聲學(xué)層之間的接觸面積,Si是各聲學(xué)層與左右側(cè)板的接觸面積。為各聲學(xué)層與四周邊界的模態(tài)耦合函數(shù),表達式為:

式中:φin是各聲學(xué)層在四周剛性邊界下的模態(tài)函數(shù),ψj是各聲學(xué)層四周彈性板的模態(tài)振動位移。將各聲學(xué)層及側(cè)板模態(tài)函數(shù)代入(20)式,可得各聲學(xué)層與左右側(cè)板的模態(tài)耦合函數(shù)為:
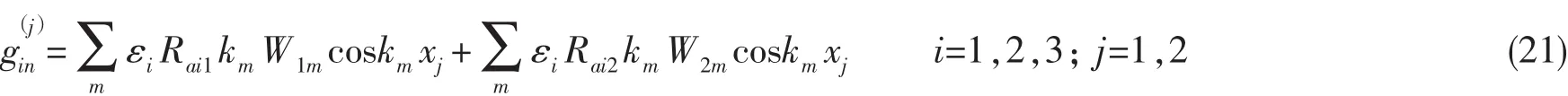
同理,可得上層平板與第一層聲學(xué)層的模態(tài)耦合函數(shù)為:

第一層虛擬膜與第一層聲學(xué)層的模態(tài)耦合函數(shù)為:

兩層虛擬膜與第二層聲學(xué)層的模態(tài)耦合函數(shù)為:

第二層虛擬膜與第三層聲學(xué)層的模態(tài)耦合函數(shù)為:

下層平板與第三層聲學(xué)層的模態(tài)耦合函數(shù)為:

具體推導(dǎo)過程和Rai1、Rai2、Rai3和Rai4(i= 1 ,2,3,4 )的表達式見附錄B。
按文獻[17]的處理方法,可以得到第一層和第三層聲學(xué)層分別作用于上、下層平板的廣義模態(tài)力p1m和p3m:
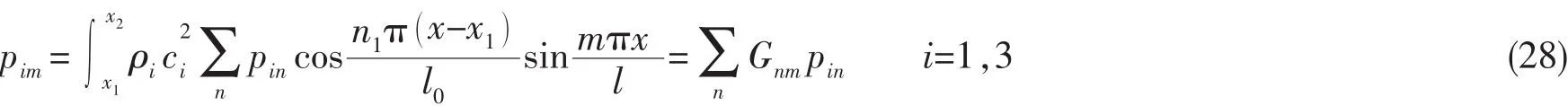
式中:
當i=1時,耦合系數(shù);當i=3時,耦合系數(shù)
求解在內(nèi)部聲壓作用下第一層與第二層、第二層與第三層之間虛擬膜的振動方程,利用虛擬膜剛度和質(zhì)量為0的假設(shè)條件,可得各聲學(xué)層之間的模態(tài)聲壓耦合方程:

直接引用文獻[18]的結(jié)果,忽略外場模態(tài)互輻射阻抗,外場輻射聲壓作用在下層平板上的廣義模態(tài)力可以表示為:

Zmp是下層平板的外場輻射聲阻抗。 將(13)式、(17)式、(28)式和(31)式代入到上、下平板的振動模態(tài)方程(12)式中,得到上、下平板的振動模態(tài)耦合方程:
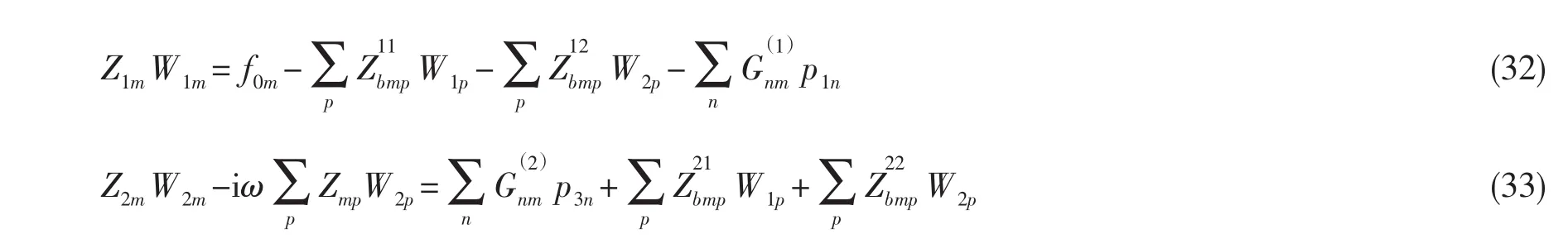
將(21)~(27)式代入(19)式,得到各聲學(xué)層與四周邊界的聲學(xué)模態(tài)耦合方程:
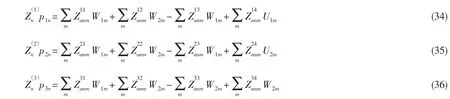
聯(lián)立(32)~(36)式及(29)、(30)式并表示成矩陣的形式,有:

式中:
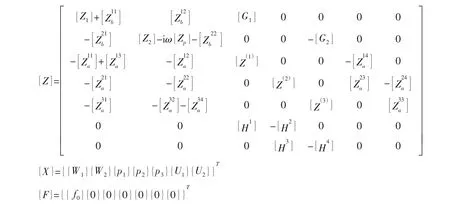
求解方程組(37)可得上下板的振動模態(tài)位移W1m、W2m,進一步可計算外場聲輻射。
2 計算分析
液艙上層平板受集中點力作用,計算液艙上下層平板振動及下層平板輻射向外場的輻射聲功率。計算所取的幾何及材料參數(shù)由表1給出。

表1 液艙模型基本參數(shù)Tab.1 Paremeters of the water tank model
為了校驗計算模型,取液艙內(nèi)介質(zhì)為空氣,側(cè)板材料為鋼,且厚度取薄為1 mm,振速參考級取為1×10-9m/s,計算得到的上下層平板均方振速與它們分別受點力激勵的均方振速比較參見圖2。可見,當液艙上、下層平板之間的聲振耦合較弱時,上一節(jié)所建模型計算結(jié)果與平板振動單獨計算結(jié)果吻合,間接地說明了計算模型及結(jié)果的合理性與正確性。
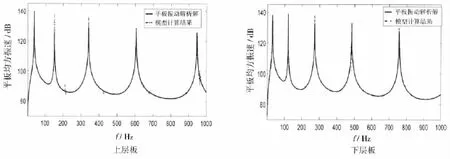
圖2 上、下層平板振動校核結(jié)果Fig.2 Calculation check for the vibraion of upper and lower panel
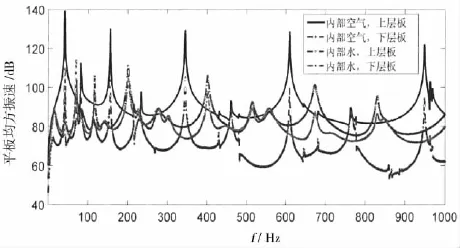
圖3 液艙內(nèi)部為不同聲介質(zhì)時上下層平板的振動比較Fig.3 Comparison of the vibration of upper and lower panel for the different internal medium
(1)液艙內(nèi)部聲場與上下層平板聲振耦合特性
取側(cè)板厚度為10 mm、液艙深為0.8 m,計算液艙內(nèi)部充滿水和充滿空氣兩種情況下,點激勵作用于上層平板時,上下平板的振動以及外場輻射聲功率,結(jié)果分別見圖3和圖4。當液艙內(nèi)部為空氣時,上層板和下層板之間聲場耦合較弱,聲能量的主要傳遞通道為側(cè)板,上下層平板振動量級相差較大。圖3中,由于連接側(cè)板給上層平板提供了額外的剛度導(dǎo)致前5階模態(tài)頻率變高。在外場流體負載的影響下,下層板前四階模態(tài)響應(yīng)頻率向低頻偏移,由于側(cè)板連接剛度的影響大于流體負載的影響,第五階模態(tài)響應(yīng)頻率向高頻偏移。液艙內(nèi)部聲介質(zhì)為水時,內(nèi)部聲場與上下平板振動強耦合,上下層平板振動的量級比較接近。
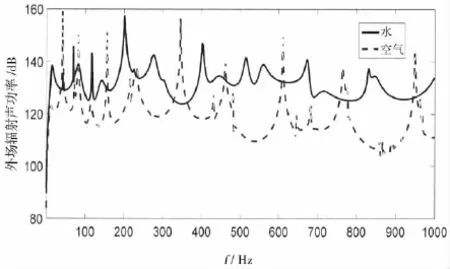
圖4 液艙內(nèi)部為不同聲介質(zhì)時外場輻射聲功率比較Fig.4 Comparion of the external acoustic radiation power for different internal medium
由圖4可見,當液艙內(nèi)部為空氣時,上層平板振動通過側(cè)板傳遞引起的下層板振動,是外場聲輻射產(chǎn)生的主要途徑,相應(yīng)的量級明顯小于液艙內(nèi)充水的情況。液艙充水時,雖然內(nèi)部水介質(zhì)對上下層平板都提供了附加質(zhì)量,但由于艙內(nèi)聲場與上下平板振動的強耦合,加上側(cè)板的振動傳遞作用,下層平板的振動明顯大于艙內(nèi)為空氣介質(zhì)的情況,使得整個頻段上外場輻射聲功率的量級更大。
(2)側(cè)板不同材料參數(shù)及結(jié)構(gòu)參數(shù)對振動傳遞的影響
液艙內(nèi)充滿空氣,側(cè)板厚度為5 mm,材料分別為鋼(E=20.6e10Pa)和玻璃鋼(E=1.576e10Pa),圖5給出了上層板受點激勵時,側(cè)板為鋼和玻璃鋼情況下,下層板的振動比較。由圖5可以看到,在上層板的固有頻率處,下層板的振動明顯增大,說明側(cè)板剛度越大,傳遞的振動能量越大。而在液艙聲場的固有頻率處,下層板的振動響應(yīng)基本沒有變化。
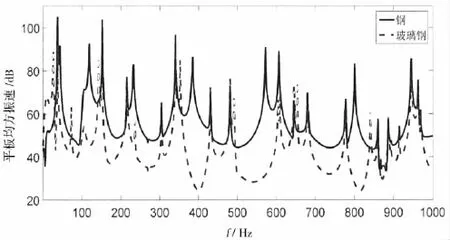
圖5 不同材料側(cè)板時下層板振動比較Fig.5 Comparison of the vibration of lower panel with different material used by side panel
圖6中,鋼側(cè)板厚度由3 mm增加到10 mm,通過側(cè)板傳遞的能量增大,下層板振動的量級也變大。且隨著側(cè)板厚度變大,側(cè)板附加在上層板上的剛度變大,傳遞到下層板上的振動響應(yīng)頻率向高頻偏移,側(cè)板傳遞途徑逐漸占主導(dǎo)作用,液艙內(nèi)部聲場固有頻率處的振動峰值則被慢慢“淹沒”。
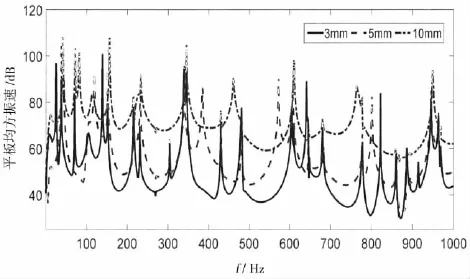
圖6 不同厚度側(cè)板時下層板振動比較Fig.6 Comparison of the vibration of lower panel with different material used by side panel
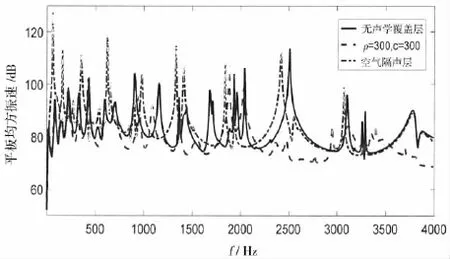
圖7 敷設(shè)不同參數(shù)覆蓋層,上層板振動對比Fig.7 Comparison of the vibration of upper panel lined with acoustic coating of different parameters

圖8 敷設(shè)不同參數(shù)覆蓋層,下層板振動對比Fig.8 Comparison of the vibration of lower panel lined with acoustic coating of different parameters
(3)聲學(xué)覆蓋層降噪效果分析
側(cè)板材料為鋼,厚度為12 mm。覆蓋層厚度3 cm,等效密度為300 kg/m3,等效聲速為300 m/s。圖7、圖8分別給出了敷設(shè)聲學(xué)覆蓋層情況下,上層板和下層板的振動響應(yīng)。空氣隔聲層的質(zhì)量較輕,圖7中可以看到有空氣隔聲層的情況下,由于沒有重流體負載的作用,上層板的振動在低頻處變大。振動量級與上層板自由振動的情況接近。說明隔聲層能夠有效減弱液艙內(nèi)聲場與平板振動的耦合作用。當覆蓋層等效密度變大為300 kg/m3時,低頻段的振動響應(yīng)與沒有敷設(shè)覆蓋層的情況幾乎沒有區(qū)別。在1 000 Hz以上由于聲學(xué)覆蓋層的阻尼效應(yīng),頻段振動響應(yīng)變小。圖8中可以看到,通過敷設(shè)聲學(xué)覆蓋層,下層板的振動在800 Hz以上的頻段有明顯抑制。但由于側(cè)板的振動傳遞作用,敷設(shè)聲學(xué)覆蓋層與空氣隔聲層對下層板振動響應(yīng)的影響沒有顯著差別。不同算例下外場輻射聲功率的對比由圖9給出。外場輻射聲功率在800 Hz以上頻段得到有效抑制,而在800 Hz以下的頻率范圍內(nèi),敷設(shè)聲學(xué)覆蓋層與空氣隔聲層都沒有明顯降噪效果。
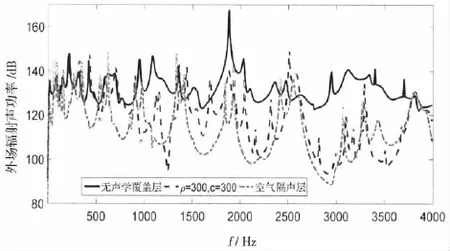
圖9 敷設(shè)不同參數(shù)覆蓋層,外場輻射聲功率對比Fig.9 Comparison of the external acoustic radiation power lined with acoustic coating of different parameters
若將側(cè)板材料換成玻璃鋼,降低側(cè)板的連接剛度。由于玻璃鋼側(cè)板的振動傳遞較弱,艙內(nèi)聲學(xué)覆蓋層尤其是空氣層的聲場隔離作用增強。從圖10中可以看到,用空氣隔聲層隔離液艙內(nèi)聲場的傳遞并用玻璃鋼側(cè)板減小上下平板間的振動傳遞,使得外場輻射聲功率在全頻段上都有明顯的降低。圖11中,聲學(xué)覆蓋層的等效密度參數(shù)遠大于空氣密度,可以看到在500 Hz以上的頻率內(nèi)外場輻射聲功率有明顯的降低,在500 Hz以下的某些頻率也有10 dB左右的降噪效果。
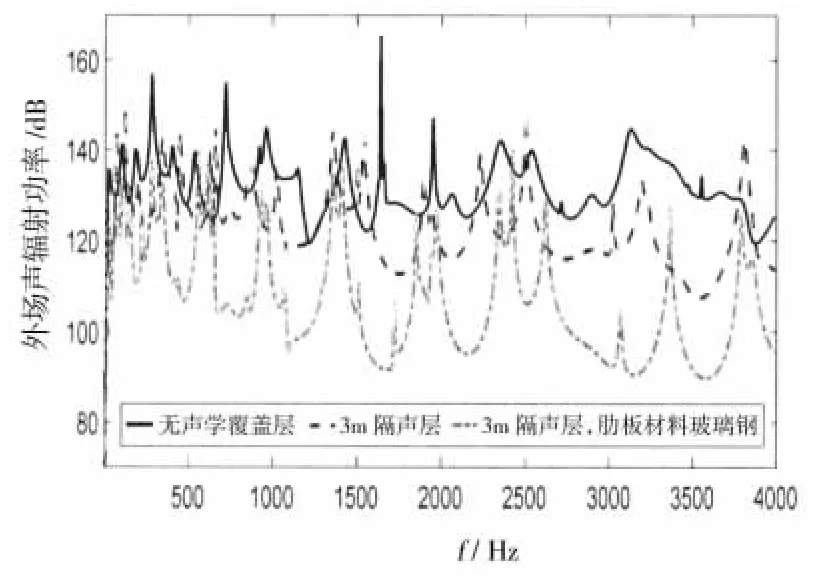
圖10 敷設(shè)3 cm空氣隔聲層,側(cè)板材料換成玻璃鋼Fig.10 External acoustic radiation power with 3 cm air gap and fiberglass side panel
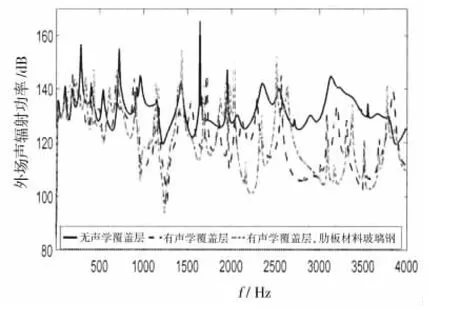
圖11 敷設(shè)3 cm聲學(xué)覆蓋層,側(cè)板材料換成玻璃鋼Fig.11 External acoustic radiation power with 3 cm acoustic coating and fiberglass side panel
圖12中,覆蓋層的厚度從3 cm增大到5 cm,聲波在覆蓋層中的共振頻率發(fā)生變化,使外場聲輻射的峰值發(fā)生頻移。在800 Hz以下,較厚的聲學(xué)覆蓋層對輻射聲功率的控制更有效,而在800 Hz以上,較薄的聲學(xué)覆蓋層對輻射聲功率的控制更有效。這一結(jié)論與Antonio[4]的研究結(jié)果是一致的。
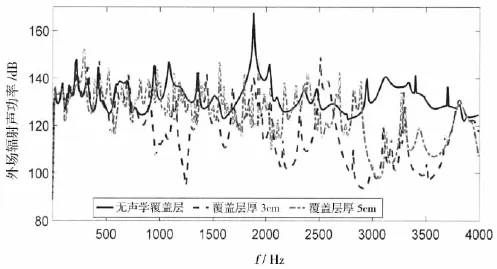
圖12 不同覆蓋層厚度,外場輻射聲功率對比Fig.12 Comparison of external acoustic radiation power with acoustic coating of different thickness
3 結(jié) 論
本文采用解析方法,建立了舷間液艙結(jié)構(gòu)振動與內(nèi)外聲場的聲振耦合模型,計算分析了液艙側(cè)板及內(nèi)部介質(zhì)對振動傳遞和外場聲輻射的影響規(guī)律。基于阻抗失配原理,通過敷設(shè)聲學(xué)覆蓋層對外場聲輻射進行控制,選用復(fù)合材料側(cè)板,能夠進一步降低外場輻射聲功率。經(jīng)過分析計算,得到如下結(jié)論:
(1)液艙內(nèi)部為空氣,平板結(jié)構(gòu)與液艙內(nèi)部聲場耦合較弱的情況下,上下層平板間振動傳遞主要途經(jīng)側(cè)板。振動傳遞隨著側(cè)板剛度的變大而變大。液艙內(nèi)部為水介質(zhì)時,平板結(jié)構(gòu)振動與液艙內(nèi)部聲場耦合變強,內(nèi)部介質(zhì)和側(cè)板與平板間的聲振耦合都是能量傳遞的主要途徑。
(2)液艙內(nèi)部充滿水介質(zhì)時,內(nèi)部聲介質(zhì)增加了上層平板的負載,使得上層平板的振動量級變小。但由于液艙內(nèi)部聲場與平板的耦合增強,還是提高了液艙向外輻射聲能的效率。
(3)敷設(shè)聲學(xué)覆蓋層并改變側(cè)板的材料,能夠有效降低外場輻射聲功率。用聲學(xué)覆蓋層隔離聲場傳遞并改用玻璃鋼作為側(cè)板材料,在500 Hz以上的頻段取得了較明顯的降噪效果。而在更低頻率范圍內(nèi),外場輻射聲功率的控制需要尋求別的控制方法。

將(A.1)式代入(5)式可以求得(A.1)式中的待定系數(shù)為:
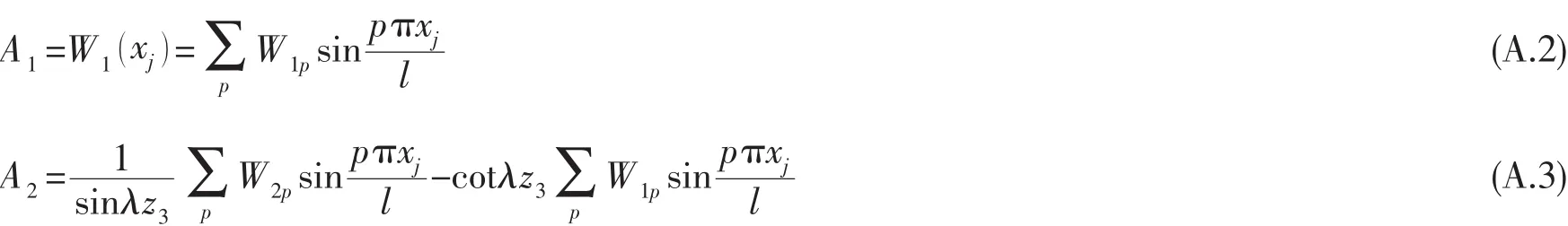
將(A.2)、(A.3)式代入(A.1)式得到側(cè)板面內(nèi)振動表達式,再代入(4)式中,可得x=xj(j=1,2 )處側(cè)板面內(nèi)振動對上下平板的廣義模態(tài)力表示式(13)式。其中

2.側(cè)板面外振動與上下層平板相互作用力
求解(3)式,側(cè)板面外振動位移的表達式為:

式中:
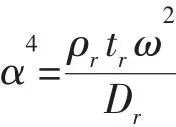
將(A.4)式代入(6)、(7)式可得:
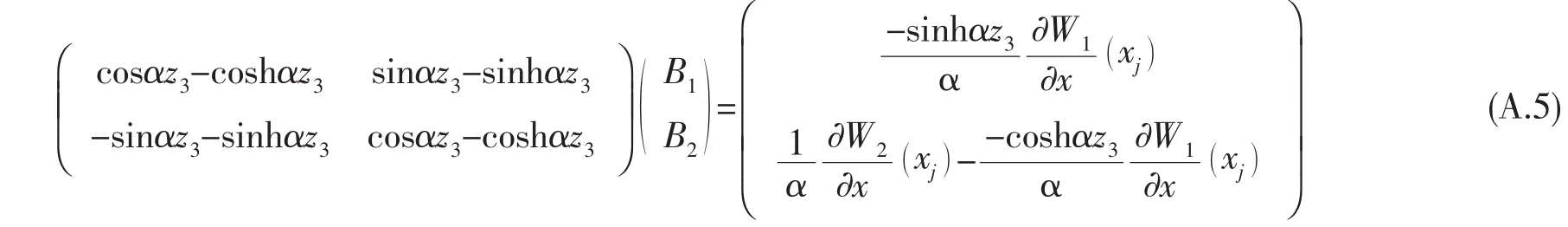
求解(A.5)式可得待定系數(shù)B1和B2為:
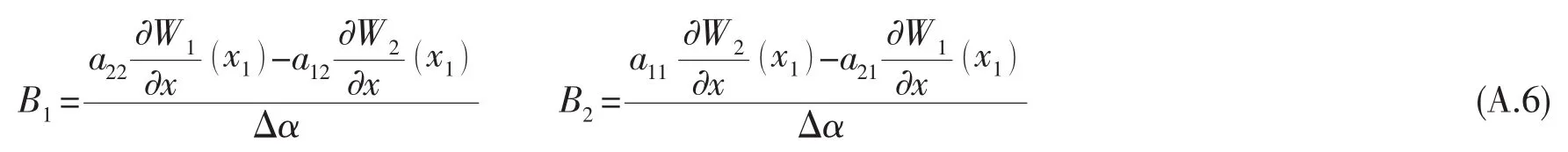
式中:
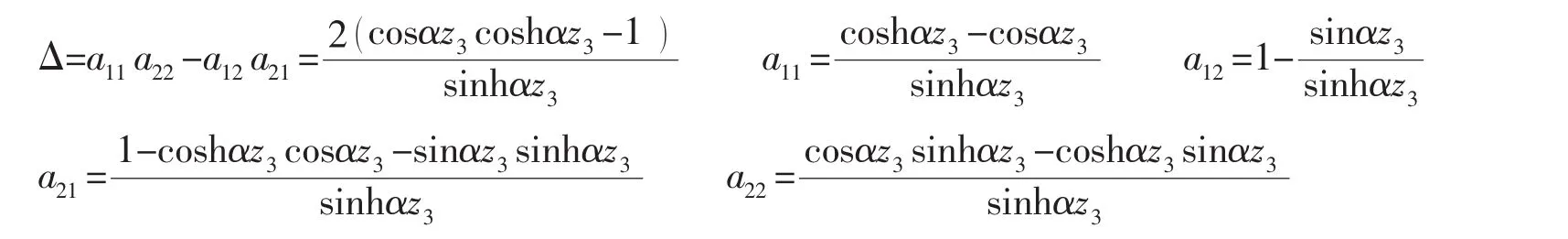
將(A.4)式代入(14)式,可得側(cè)板對上下平板的力矩表達式:
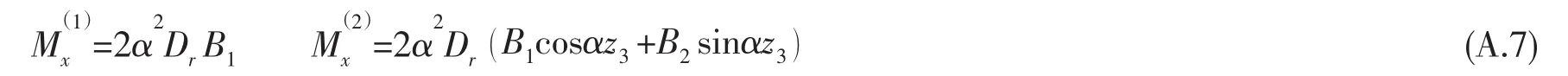
再將(A.6)式代入(A.7)式,得到側(cè)板與上下彈性板的作用力矩表達式(15)、(16)式,按文獻[1]的處理方法可得在x=xj(j=1,2 )處側(cè)板面外振動對上下平板(i=1,2 )作用的廣義模態(tài)力表達式。其中:
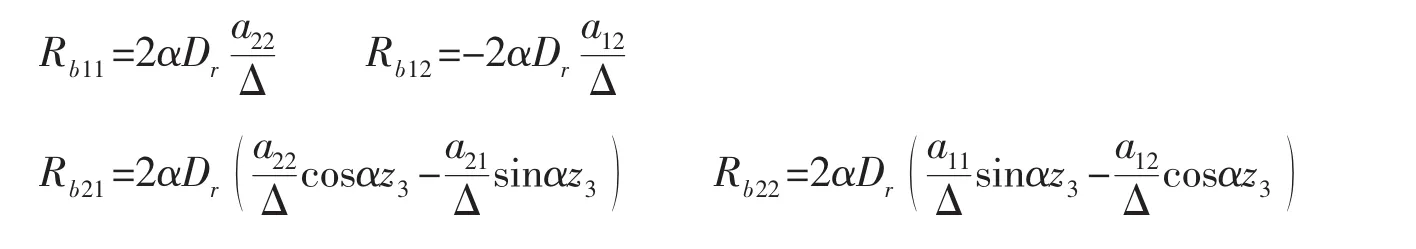
附錄B 各聲學(xué)層與四周邊界的耦合關(guān)系
假設(shè)液艙側(cè)板彎曲振動位移解為:

式中:
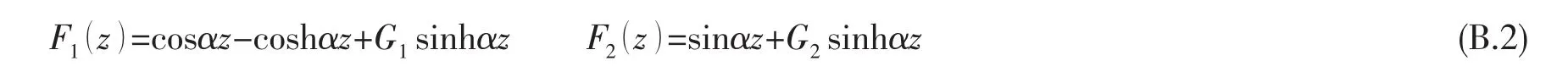
G1、G2的表達式為:

將(B.1)~(B.3)式代入(20)式,可得聲學(xué)層與側(cè)板的模態(tài)耦合函數(shù):
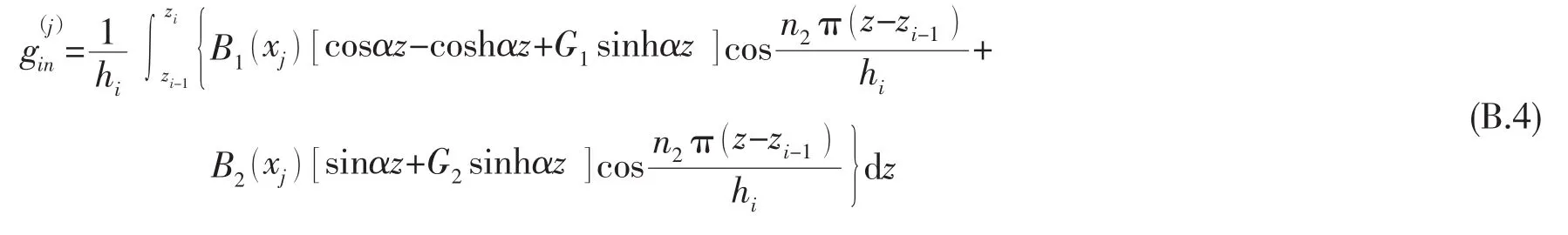
積分可得:
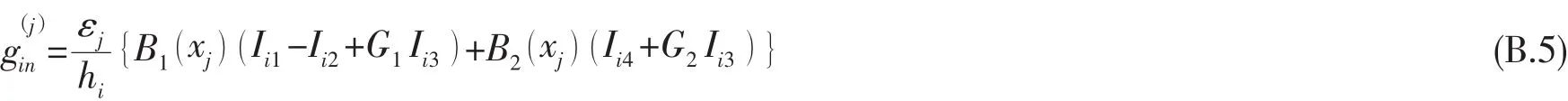
再將(A.6)式代入(B.5)式,則可得(21)式,其中:
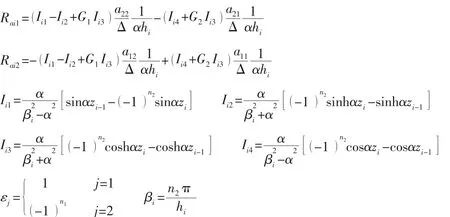
采用類似的推導(dǎo),可得各聲學(xué)層與平板和虛擬膜的模態(tài)耦合系數(shù):


