金屬阻尼器參數與金屬阻尼器減震效果相關性研究

侯逸冰 嚴 焱 張新鈺

(江蘇科技大學，江蘇鎮(zhèn)江 212000)

1 概述

消能減震設計是通過消能裝置耗散或吸收地震能量，把結構物中的某些構件設計成消能構件或在結構物的某些部位裝設阻尼器，立足于“耗能”。當外部遭遇風荷載或小震作用時，消能構件和阻尼器處于彈性狀態(tài)，結構本身具有的抗側移剛度足以滿足正常的使用要求;遭遇強烈地震作用時，消能構件或阻尼器率先進入非彈性狀態(tài)，從而保護主體結構在強震中免遭破壞耗地震能量，從而減小結構在地震中的相對動能或勢能以及結構的變形能。消能減震技術克服了傳統(tǒng)“硬碰硬”式的抗震設計方法，為建筑的抗震設計和抗震加固提供了一條嶄新的途徑，具有安全、適用、經濟、技術合理等優(yōu)越性。金屬在進入塑性狀態(tài)后具有良好的滯回特性，并在彈塑性滯回變形過程中能吸收大量能量，因此被用來制作不同類型的阻尼器。將金屬阻尼器在結構不同的位置設置，將所得結果相互分析比較，從而得到金屬阻尼器在高層鋼框架結構中的最優(yōu)布置位置;以等效線性化理論，能量平衡理論以及倍數法理論的消能減震結構設計方法為基礎，分別計算結構附加阻尼器的阻尼量。研究大多和金屬阻尼器的位置以及數量相關。本文進一步研究金屬阻尼器內部因素:屈服強度、剛度、屈服位移以及三者對附加金屬阻尼器消能減震體系的影響。

2 金屬阻尼器參數與滯回曲線

金屬阻尼器的滯回曲線概括了阻尼器的剛度、強度、屈服位移等力學特性，滯回曲線環(huán)所圍成的面積可衡量阻尼器吸收能量的能力。圖1用雙線型模型來表示金屬阻尼器的恢復力—位移滯回曲線。圖2為滯回曲線骨架模型。

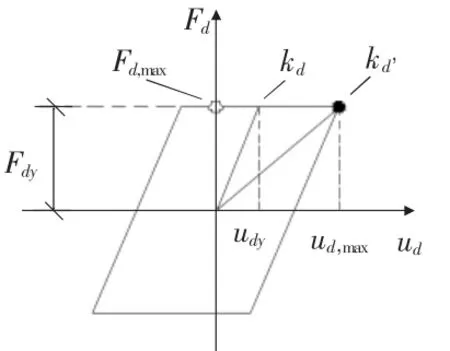
圖1 金屬阻尼器滯回曲線圖

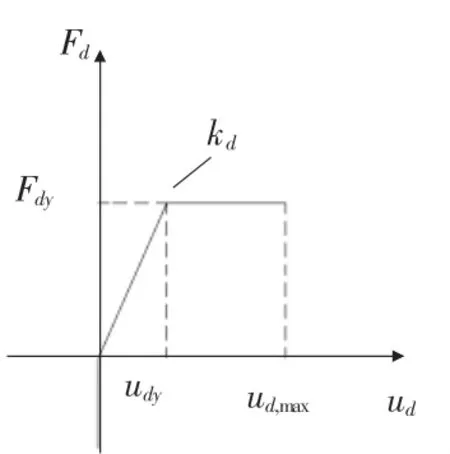
圖2 金屬阻尼器滯回曲線骨架模型

金屬阻尼器的三個主要參數:剛度、屈服位移、屈服強度分別對應滯回曲線骨架模型中的第一剛度kd、第一屈服位移udy、屈服強度Fd。三者之間的關系符合式(1)。

為了研究第一剛度kd、第一屈服位移udy、屈服強度Fd對金屬阻尼器減振效果的影響，將原結構附加的金屬阻尼器，并分下列兩種情況來討論消能減震體系的地震反應:1)保持屈服位移udy不變，改變阻尼器抗側剛度kd和屈服強度Fd;2)保持阻尼器抗側剛度kd不變，改變屈服位移udy和屈服強度Fd。

3 計算模型

原結構采用單質點模型，并附加金屬阻尼器組成消能減震體系，連接形式如圖3所示。原結構抗側剛度kf=1.18×108N/m，質量為:m=1.55×107kg，其自振周期為2.276 s。圖3中kf為原結構抗側剛度，c為原結構內部粘滯阻尼，kd為金屬阻尼器的抗側剛度。

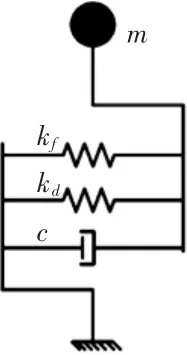
圖3 單質點消能減震體系

4 振動微分方程和地震動

消能減震體系在地震作用下的振動微分方程為:

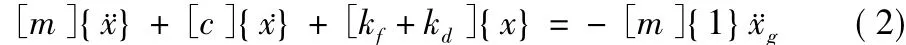
其中，［m］為結構質量;［c］為結構內部粘滯阻尼矩陣;kf為主結構的抗側剛度;kd為附加的金屬阻尼器抗側剛度，在金屬阻尼器屈服前后，kd的值也會發(fā)生著變化。{¨x}，{x}，{x}分別為結構加速度、速度、位移反應量;¨xg為地面地震動加速度。

本文采用兩條地震波對結構進行彈塑性時程分析，使用wilson-θ法進行結構地震響應計算。由于改變阻尼器剛度后，整個結構的周期也會發(fā)生變化，而自然波的頻譜特性對基本周期不同的結構產生的地震作用不同，所以采用人工波進行時程分析，稱為建筑波，作用時間為60 s，時間間隔為0.01 s，其加速度時程曲線如圖4所示。為了得出結構在罕遇地震和多遇地震作用下的情況，設定地震波加速度峰值為5 m/s2和0.7 m/s2。

5 設置金屬阻尼器消能減震分析

5.1 保持屈服位移udy不變，改變阻尼器抗側剛度kd和屈服強度Fd

設定金屬阻尼器的抗側剛度kd分別為原結構抗側剛度的1倍，2倍，3倍，…，20倍，0倍情況即為原結構，金屬阻尼器的屈服位移udy均為0.004 33 m。分別將附加不同金屬阻尼器的結構命名為結構－1，結構－2，…，結構－20，結構－0為原結構。

對附加不同金屬阻尼器的結構進行時程分析，得出結構在地震波的罕遇和多遇地震作用下的地震響應。分析結果如下:

圖5，圖6分別表示附加各個金屬阻尼器的結構在地震作用下的最大位移反應值、最大速度反應值。隨著阻尼器抗側剛度kd和屈服強度Fd的增大，結構的最大位移值、最大速度反應值呈降低趨勢。在罕遇地震作用下，結構的最大位移值、最大速度反應值下降趨勢明顯，而結構在多遇地震作用下，最大位移值、最大速度反應值下降逐漸變緩。

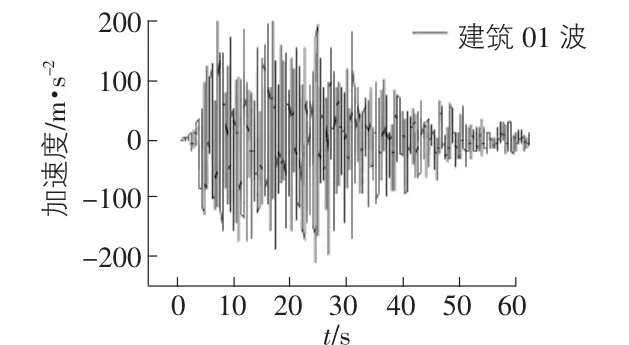
圖4 地震波

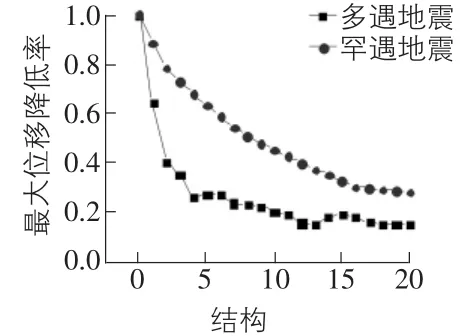
圖5 最大位移反應值降低率

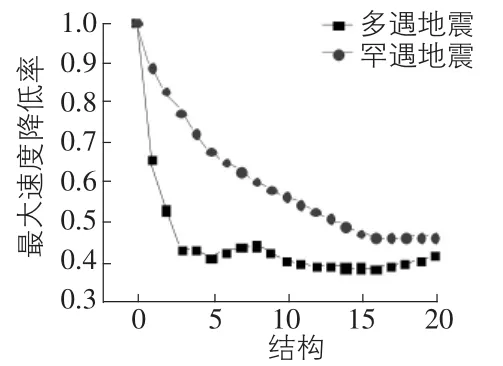
圖6 最大速度反應值降低率

圖7 表示各個結構在罕遇地震和多遇地震作用下的最大加速度反應值。結構在罕遇地震作用下，最大加速度反應值隨著金屬阻尼器抗側剛度的增加有明顯的降低趨勢;而結構在多遇地震的作用下，最大加速度值隨著金屬阻尼器抗側剛度kd和屈服強度Fd的逐漸增大，呈先降低后增大的趨勢。

通過比較推斷，增加金屬阻尼器的抗側剛度kd和屈服強度Fd，在罕遇地震作用下，金屬阻尼器的減震效果逐漸增大;在多遇地震作用下，金屬阻尼器的減震效果先增大，然后逐漸變小。體系經受多遇地震的地震波時，金屬阻尼器抗側剛度為原結構抗側剛度的5倍為最佳效果。因為若繼續(xù)增大倍數，結構地震反應值(位移值、速度值)減小不多，而體系的加速度值增大很多。

5.2 保持阻尼器抗側剛度kd不變，改變屈服位移udy和屈服強度Fd

將原結構附加金屬阻尼器，抗側剛度kd=1.18×108N/m，初始屈服位移udy=0.004 33 mm。保持金屬阻尼器的抗側剛度，改變金屬阻尼器的屈服位移，分別為原位移的1倍，2倍，3倍，…，20倍。分別將附加不同倍數金屬阻尼器的結構命名為結構－1，結構－2，…，結構－20，結構－0為原結構。對附加不同金屬阻尼器的結構進行時程分析，得出結構在地震波的常遇和罕遇地震作用下的地震響應。分析結果如下:圖8～圖10分別表示附加各個金屬阻尼器的結構在地震作用下的最大位移反應值、最大速度反應值、最大加速度反應值。隨著阻尼器屈服位移udy和屈服強度Fd的增大，體系在罕遇地震作用下，體系的最大位移值、最大速度反應值下降趨勢明顯，而后趨于平緩;體系的最大加速度值呈下降趨勢。體系在多遇地震作用下，最大位移值、最大速度反應值、最大加速度反應值先下降，后上升，最后趨于某一定值。

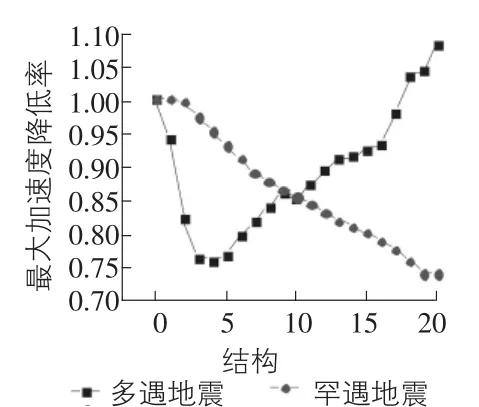
圖7 最大加速度反應值降低率（一）

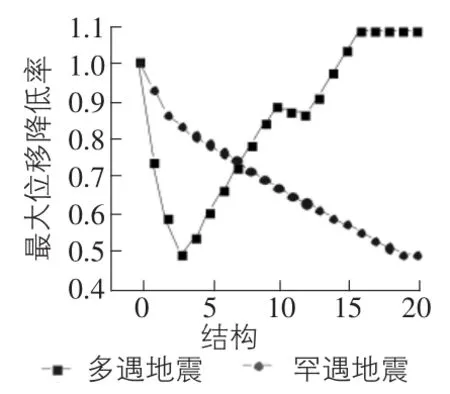
圖8 最大位移反應值降低率

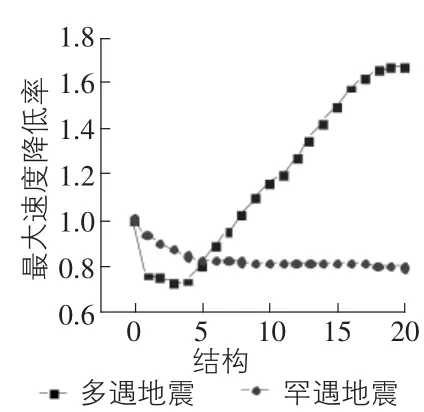
圖9 最大速度反應值降低率

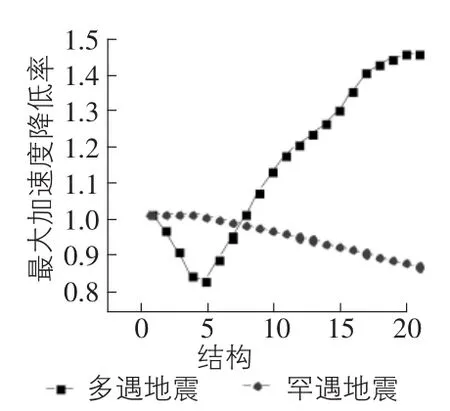
圖10 最大加速度反應值降低率（二）

通過比較推斷，金屬阻尼器增加屈服位移udy和屈服強度Fd，在增幅不大時會使得金屬阻尼器的減震效果變好，隨著倍數的增加，金屬阻尼器的減震效果逐漸變小，罕遇地震作用下的金屬阻尼器減震效果趨于平緩;多遇地震作用下的金屬阻尼器減震的能力逐漸消失。體系經受多遇地震的地震波時，金屬阻尼器屈服位移為初始屈服位移的3倍為最佳效果。繼續(xù)增大倍數，結構地震反應值:位移值、速度值、加速度值會呈增大趨勢。

6 結語

通過對上述算例模型分析，得出如下結論:1)附加金屬阻尼器的消能減震結構，隨著金屬阻尼器的抗側剛度kd和屈服強度Fd的增大，金屬阻尼器的減震效果變好，當結構經受多遇地震時，金屬阻尼器抗側剛度為原結構抗側剛度的5倍為最佳效果。2)金屬阻尼器隨著金屬阻尼器的屈服位移udy和屈服強度Fd的增大，金屬阻尼器的減震效果呈現略微增大后持續(xù)變小的情況。當結構經受多遇地震時，金屬阻尼器屈服位移為金屬阻尼器初始位移的3倍為最佳效果。