金屬橡膠的本構關系研究★

王亞杰 趙亞哥白* 任小龍 黃新宇 王 璇 韓靜怡

(東北林業大學，黑龍江哈爾濱 150040)

過去的許多試驗表明，金屬橡膠材料是一種具有良好的變形自恢復能力的非線性干摩擦阻尼材料。它具有含有良好三次非線性成分［1］的無記憶恢復力，除此還具有優秀的變形自恢復能力即記憶恢復力，金屬橡膠耗能器的恢復能力具有非線性遲滯效應，其阻尼成分既有粘性阻尼又有干摩擦阻尼。國內外現在有宏觀力學模型與微觀力學模型兩種建立金屬橡膠本構關系比較著名的方法，在建立本構關系時需考慮金屬橡膠材料諸多復雜性質。

1 建立宏觀力學模型

通常采用理論法和實驗法［2］兩種方法來建立宏觀數學本構模型，理論法常常被看做“白箱”問題，通過運用現有的定理規律，來推導判斷系統中狀態參數與作用的關系。而實驗法是直接從實驗數據出發，通過歸納總結來建立數學模型，這種情況又被稱為“黑箱”問題。但是在實際中遇到的問題往往是介于兩者之間的問題，必須將定理分析與實驗歸納融合起來來尋找解決方法，遇到這種情況可以根據部分已知特性并通過特殊處理后來推導未知參數從而確定完整的狀態方程，這種問題常常被稱之為“灰箱”問題。目前常采用最小二乘法來確定未知參數，相比于極大似然法，輔助變量法等其他方法，最小二乘法具有概念簡單，使用情況更加廣泛等很多優點，用其求得的估計值具有最優統計特性，可以實現使得實驗數據在平方誤差意義上達到最小誤差的效果。其實現過程為:假定一組變量含有m個元素x=(x1，x2…，xm)與某個變量z成某種確定的線性關系，如下:

方程中:θ=(θ1，θ2，…，θm)為一組參數并且是常數，式中 θi是未知的，該未知參數的取值可以通過在不同時刻觀測變量z和x的關系來估計。假設已經在t1，t2，…，tn時刻對二者作了n次觀測，其觀測數據用 z(i)和 x1(i)，x2(i)，…，xm(i)，(i=1，2，…，n)兩組參數來代表，如此便可以得到以下方程:

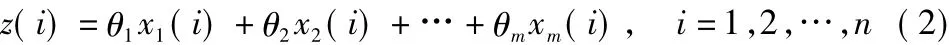
上述方程又可定義為回歸函數，θm則為回歸系數。其又可寫成矩陣形式如下所示:

式中:

為了估計參數θ，前提是m≥n。如果m與n值相等，那么θ值則有唯一解，即是:

再設 J=(Z －Xθ)T(Z － Xθ)=ZTZ － θTXTZ － ZTXθ+θTXTXθ。

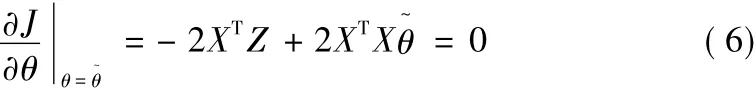
從而解得θ～=(XTX)－1XTZθ即為在最小二乘法基礎上的估計值。

白鴻柏、黃協清［1］通過運用宏觀力學分析方法，并使用最小二乘法對各參數進行識別取值來確定金屬橡膠隔振器中的力—位移之三次非線性遲滯泛函本構關系，又得到三階非線性多項式的彈性力和等效粘性阻尼力疊加組成了金屬橡膠的恢復力的結論。姜洪源［3］曾提出建立金屬橡膠構件的變形模型可以通過實驗的理論方法來實現。

2 細觀力學模型的研究

由于承受徑向和軸向荷載的微螺旋彈簧沖壓使得金屬橡膠材料的細觀結構特征成型，則金屬橡膠的剛度由微螺旋彈簧的剛度決定。在分析中可忽略彈簧絲軸力和剪力的影響，只考慮彎矩影響。陳艷秋曾提出用小曲梁的串并連來描述材料總體剛度，可將雜亂金屬絲看成多層微小彈簧，每一個彈簧都有一定剛度，它們共同組成金屬橡膠總的剛度。彭威，白鴻柏［5］也曾通過引用新的材料參數鋪層比例系數來建立微彈簧組合變形的細觀本構模型。

3 建立硬化折線本構模型

為建立金屬橡膠本構模型，可以運用實驗法，該方法的簡化分析模型不僅便于計算，簡化了MR耗能減振結構的地震反應分析方法，而且能夠表征材料的應變硬化特征，與試驗曲線符合。根據實驗法原理，在室溫下對相對密度為0.27，加載頻率為1 Hz，并處于最大應變幅值為20%的應力—應變曲線部分的金屬橡膠材料進行擬合，其相應的應力應變曲線如圖1所示。

構建模型可以利用MATLAB計算軟件來實現:第一步將MR應力—應變曲線分成兩部分，分別為加載段和卸載段;然后對前者采用局部依次擬合的方法，來得到圖中的OA與AB曲線段，從而得到簡化模型的強化應力、初始彈性模量等重要參數，最后確定BC段和CO段依據原則為能量相等，使簡化模型與實際曲線包圍相等的面積(見圖2)。

圖1 OMR-D“τ — γ”遲滯回線

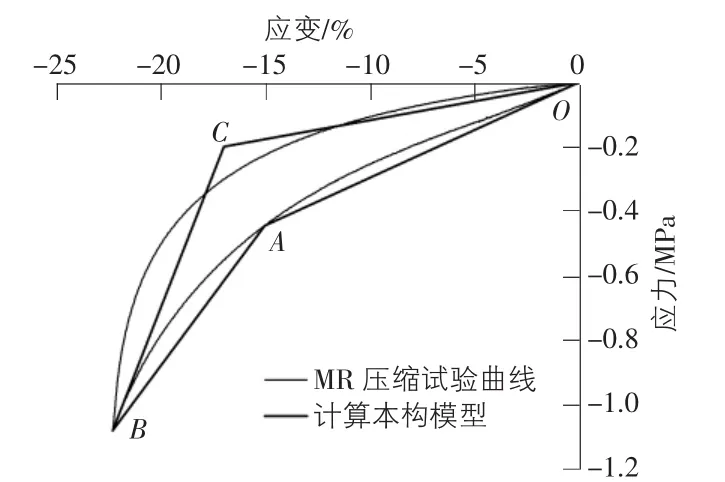
圖2 應變硬化折線本構模型擬合

下面將以此為例來編制計算程序，其詳細步驟如下所述:

1)把名義應力、名義應變根據相應轉換關系轉換為真實應力與應變，將數據拷入txt文件中，以便MATLAB讀取。

2)將原點和應力最大值作為擬合折線的兩個點，近似讀取中間加載點的坐標，寫入系統，bx，by為選定剛度變化拐點坐標，cx，cy為最大橫縱坐標。

3)輸出面積差矩陣。

豎方向223個點表示應變點，i=1∶223，表示曲線最大橫坐標值乘以10，縱坐標j=1∶20，表示有20個點。

4)計算步驟，假設已經確定了(15，04)為加載段拐點的坐標，并確定了(22，3)為曲線最大的點的坐標，這時卸載段的橫坐標應該處于這兩個坐標之間，若此時取x=19為卸載拐點橫坐標，那么190那一行就是在矩陣里面對應的，找到這行最小面積差的那個點0.233 7，j=8，將其代入 for j=1∶20，y=(j/2 －1) × ( －1) ×0.1 進行處理計算，便可以得到y，此時，便確定了卸載點的縱坐標。

注意事項:

1)根據面積最小原理計算，若有兩個符合要求的卸載點，則需選擇橫坐標位置符合真實規律的點。

2)卸載點對應的橫坐標最好取中間的點(見圖3)。

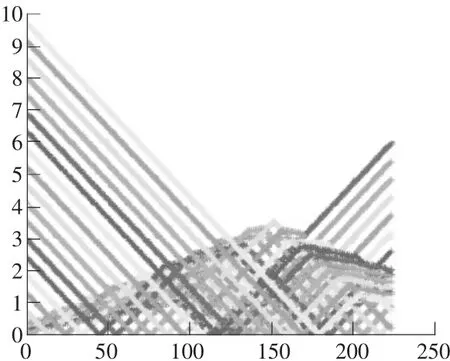
圖3 本構擬合面積相等卸載點

最后根據上述數值可以調整ABAQUS關于金屬橡膠的子程序參數，從而進一步建立本構模型。

4 結語

通過討論細觀力學模型并引入宏觀力學模型，采用最小二乘法為參數估計的方法，研究變量y與若干元素的線性關系得到回歸函數，定義誤差矢量來求得回歸系數的最小二乘的大致值。來建立金屬橡膠構件的變形模型，在室溫下相對密度為0.27，加載頻率為1 Hz，并處于最大應變幅值為20%的應力—應變曲線部分的金屬橡膠材料進行擬合，對實驗結果按照包絡面積相等原則，通過MATLAB計算軟件來處理，從而得到應變硬化折線本構模型。下一步要研究如何建立金屬橡膠阻尼器的剪力墻—連續梁結構分析模型，調整ABAQUS的子程序參數，使金屬橡膠本構模型更加具體化，提高其可靠性。