基于ANSYS對某含有凹坑缺陷發酵罐的靜力分析

時黛 林國慶

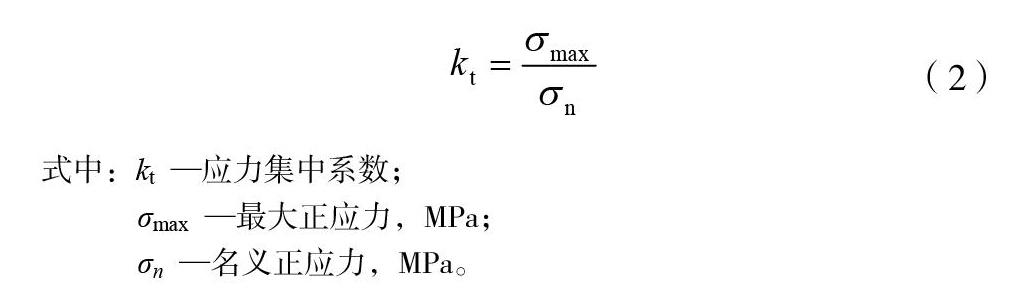
摘 ?????要：對含有凹坑缺陷的發酵罐按照GB/T19624-2004《在用缺陷壓力容器安全評定》進行安全性評定，在此基礎上利用ANSYS對不同間距的軸向排列的多凹坑進行靜力分析，得到軸向排列的多凹坑的最大應力值和應力集中系數與相鄰凹坑間距和數量的關系。經過分析可知，當相鄰凹坑間距增大到L/X≥3.0時，各凹坑之間的應力分布幾乎無影響;應力集中系數隨著兩凹坑中心距的增加而減小，當間距L/X<3時其變化幅度較大，當L/X≥3后趨于恒定;同時最大應力值和應力集中系數與凹坑缺陷數量成正比，而與相鄰的凹坑間距成反比。

關 ?鍵 ?詞：凹坑;安全評定;靜力分析;應力集中系數

中圖分類號：TQ 051.3???????文獻標識碼：?A ??????文章編號： 1671-0460（2019）11-2564-05

Static Analysis of Fermentation Tank With Pit Defect Based on ANSYS

SHI Dai， LIN Guo-qing^*

（College of Mechanical and Electrical Engineering， Jilin Institute of Chemical Technology， Jilin Province Jilin City 132022， China）

Abstract： Safety assessment of fermentation tank with pit defect was carried out in accordance with GB/T19624-2004 "Safety Assessment of Pressure Vessels with Defects in Use". On this basis， the static analysis of multi-pits with different spacing was carried out by ANSYS， and the maximum stress value and stress concentration coefficient of multi-pits with axial arrangement and between adjacent pits were obtained. The relationship between distance and quantity showed that when the distance between adjacent pits increased to?L/X≥3.0 the stress distribution between the pits had little effect. The stress concentration factor decreased with the increase of the distance between the two pits， the variation range was larger when the distance L/X<3 and tended to be constant while the distance?L/X>3. At the same time， the maximum stress value and the concentration factor were proportional to the number of pit defects and inversely proportional to the distance between adjacent pits.

Key words： Pits; Safety assessment; Static analysis; Concentration factor

在腐蝕環境下而形成的腐蝕凹坑是引起金屬材料發生失效的主要形式之一，腐蝕凹坑形成后會導致裂紋的萌生及擴展，最終發生失效而縮短部件的使用壽命，通常雖然腐蝕速率較慢，但一旦腐蝕凹坑形成其點蝕速度卻非常快，嚴重威脅著設備的安全運行。

本文中發酵罐主要應用在沼氣工業中，其發酵物料主要為生活垃圾等帶有腐蝕性的介質，所以隨著發酵罐的運行和服役時間的推移，勢必會在罐體上產生腐蝕等，很容易在罐體的內表面形成大量的腐蝕凹坑。因凹坑缺陷破壞了結構的連續性，會使缺陷部位發生應力集中現象^[1]，同時由于發酵罐在運行時其內部物料的一些物化特性變化而使發酵罐處于復雜的工作環境中，加大了凹坑處產生裂紋及擴展的可能性，使發酵罐的承載能力及安全性受到嚴重挑戰。因此，有必要對含有不同結構尺寸及數量的凹坑進行靜力分析并進行安全評定。

1 ?凹坑尺寸的確定

發酵罐內表面的凹坑多數是因腐蝕而引起的，其表面粗糙不光滑，易引起應力集中，使安全性降低，因此在進行安全評定及應力分析前，首先應把凹坑盡量打磨光滑，使表面無明顯的腐蝕跡象^[2]，同時也要保證腐蝕凹坑從坑底到罐體內表面要過渡平緩，且不可出現急劇變化的截面，凹坑的數量以及相鄰凹坑的間距都影響著發酵罐的使用壽命，對于同一條件下凹坑所引起的應力，其軸向排列的凹坑所產生的應力要明顯高于環向排列的凹坑應力^[3]，故本文主要針對軸向排列的凹坑進行研究。

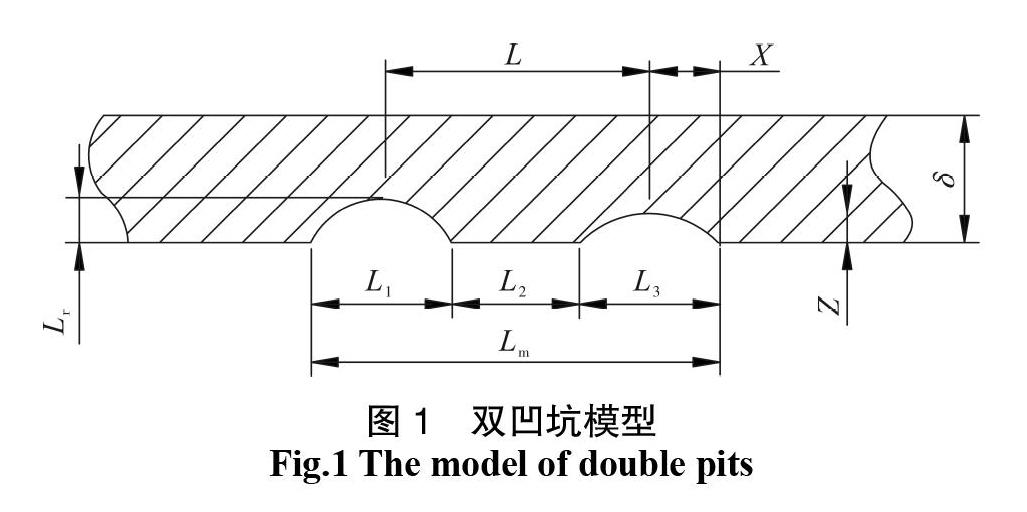
發酵罐選擇含有淺球凹坑的圓柱形殼體為研究對象，其設計壓力為0.3 MPa，設計溫度為100 ℃，盛裝生活垃圾等半固體物料，罐體所用材料為Q345R，筒體內徑為1 000 mm，焊接接頭系數為1，彈性模量209 GPa，泊松比0.28。雙凹坑的尺寸示意圖如圖1所示。

通常，腐蝕凹坑多位于罐體的內表面，凹坑深度<10%?時，其影響可忽略，但當凹坑深度達到（10%～80%）?時，需要對壓力容器重點監測^[4]。假設凹坑的x方向的寬度一致均取2X=50 mm，分析兩凹坑的圓心距與X方向寬度為不同比值時的應力分布情況，即L/X分別取0、1、2、3、4和5。為了使研究具有代表性，選擇凹坑深度為4?mm。

2 ?凹坑缺陷的安全評定

腐蝕缺陷的存在會使發酵罐的強度降低，對發酵罐的安全運行產生隱患。因此，需要對含有凹坑缺陷的發酵罐進行安全評定，以確保其安全性。

對含有凹坑缺陷的發酵罐進行安全評定的步驟為^[5]：

（1）識別缺陷;

（2）確定缺陷部位及尺寸;

（3）確定材料性能數據;

（4）計算無量綱參數G₀及判別免于評定的情況^[6];

（5）確定塑性極限載荷P_L及最高容許工作壓力P_max;

（6）安全性評定。

2.1 ?計算G₀和判別免于評定的情況

罐體表面凹坑缺陷的無量綱參數G₀可按下式計算：

????????????（1）

若G₀≤0.1則認為該凹坑缺陷是安全的或可以接受的，可免于評定;否則應進行評定。

根據公式（1）可以算出所選單凹坑的G₀值，

由上述計算可知所選凹坑G₀>0.1，按照GB/T 19624-2004中的要求須對其進行安全評定。

2.2 ?對G₀>0.1的凹坑進行安全評定

為了研究這些蝕坑對罐體的使用壽命的影響，對于無凹坑缺陷的圓柱形容器殼體的塑性極限載荷 P_L0的計算可按下式進行^[7]：

其中： —材料流動應力，取法如下：

非焊縫區凹坑，;

焊縫區凹坑，。

其中焊接接頭系數f可按實際設計條件選取，也可以根據GB150-2011或者其他標準選取。

對含有凹坑缺陷圓筒形容器的極限載荷P_L可按下式計算得到^[8]：

而最高容許工作壓力P_max的計算為：

由于P<P_max，因此單凹坑時罐體安全。

按照GB/T19624-2004《在用缺陷壓力容器安全評定》在進行評定前需要判別兩個相鄰凹坑之間是否會產生干涉，若各凹坑之間的距離滿足L₂<L_l+L₃則認為兩凹坑軸向發生相互干涉，此時將多凹坑視為同一等效凹坑^[9，10]，等效凹坑的軸向尺寸為L_m=L_l+L₂+L₃，周向尺寸為L_r。因此在多凹坑中，當相鄰兩凹坑間距為L/X≤3時，滿足將多凹坑視為同一凹坑的條件，因此按照上述計算方法同理可求得各間距下的最高容許工作壓力P_max。其他間距的凹坑在進行安全評定時因其可視為單凹坑故計算結果與單凹坑計算結果相同，最終計算結果如表1所示。

從表1中可以看出，雖然存在這些凹坑缺陷，但罐體的設計壓力始終小于最高容許工作壓力，即P<P_max，因此罐體仍處于安全狀態。

3 ?凹坑有限元分析

3.1 ?凹坑有限元計算模型

由于所取殼體與整個殼體相比較小，可以認為在幾何尺寸及載荷上具有對稱性^[11]，在用有限元建模時只需建立殼體的二分之一即可模擬出整個罐體的情況，設置好單元類型及材料屬性后，按照上述凹坑尺寸建立軸向排列的多凹坑有限元模型，劃分單元并在縱向對稱面施加對稱約束^[12]，其有限元模型如圖2所示。

3.2 ?軸向排列雙凹坑有限元結果分析

考慮凹坑在發酵罐中往往并不是單獨存在的，同時凹坑排列也是無章可循的，為了便于分析將凹坑的分布理想化處理，將其分為軸向排列和環向排列，其對發酵罐的使用壽命等由不同的影響。同時，凹坑數量及間距等因素對發酵罐的應力分布影響也不同，軸向排列的凹坑要比環向排列的凹坑危害性要大，因此本文將重點研究發酵罐的軸向排列的凹坑的應力分布情況以及對發酵罐安全性的影響（圖3）。

從圖3中可以看出，當L/X=1即單凹坑時，其最大應力為32.727 5 MPa，所在位置為凹坑的底部，至凹坑邊緣逐漸減少，凹坑周圍除在凹坑的環向方向出現對稱的局部應力減小情況外，其余地方應力幾乎相同，沒有太大的波動。

當L/X=1即兩凹坑相交時，凹坑最大應力為37.278 9 MPa，位于凹坑底部，隨著相鄰凹坑間距的增加，其最大應力呈逐漸減少的趨勢，至L/X=5時，其最大應力值為29.838 6 MPa，隨著蝕坑間距的變化至L/X≥3時，相鄰凹坑間的最大應力將在各自凹坑的底部，且其值與單凹坑的最大應力值相差不大。另外需要注意的是當L/X≤2即相鄰兩凹坑相切及相交時，其在進行應力分析時由于其中心距的原因可將其視為同一凹坑來處理，同時，隨著凹坑間距的增加，凹坑周圍的應力數值及影響區域也逐漸擴大，主要是因為兩凹坑相切及相交時其截面形狀發生突變導致其應力出現較大幅度增加，但隨著凹坑間距的增加，即間距在L/X≥3時，相鄰兩凹坑對應力的影響并不大，基本可以忽略。

3.3 ?軸向排列三凹坑有限元結果分析

從圖4中可以看出，當L/X=0即單凹坑時，最大應力為32.727 5 MPa，其值低于L/X=1、L/X=2時三凹坑的最大應力，說明在恒壓作用下，當多凹坑距離較近時所產生的應力要大于單凹坑的應力，這也意味著多凹坑時要比單凹坑危險。

當L/X≤3時，相鄰凹坑之間會發生干涉^[13]，因此在做研究時應將其視為一個凹坑。當兩凹坑相距較遠（L/X>3）時，凹坑的最大應力值與單個凹坑的最大應力差異較小，這也符合GB/T19624-2004中的規定。

3.4 ?應力集中系數的計算

由于凹坑缺陷的存在，在凹坑處勢必會產生應力集中現象，應力集中系數作為衡量應力集中程度的主要參數，在實際分析研究中具有重要意義^[14]。根據應力集中系數的定義知：

（2）

式中：k_t—應力集中系數;

σ_max?—最大正應力，MPa;

σ_n?—名義正應力，MPa。

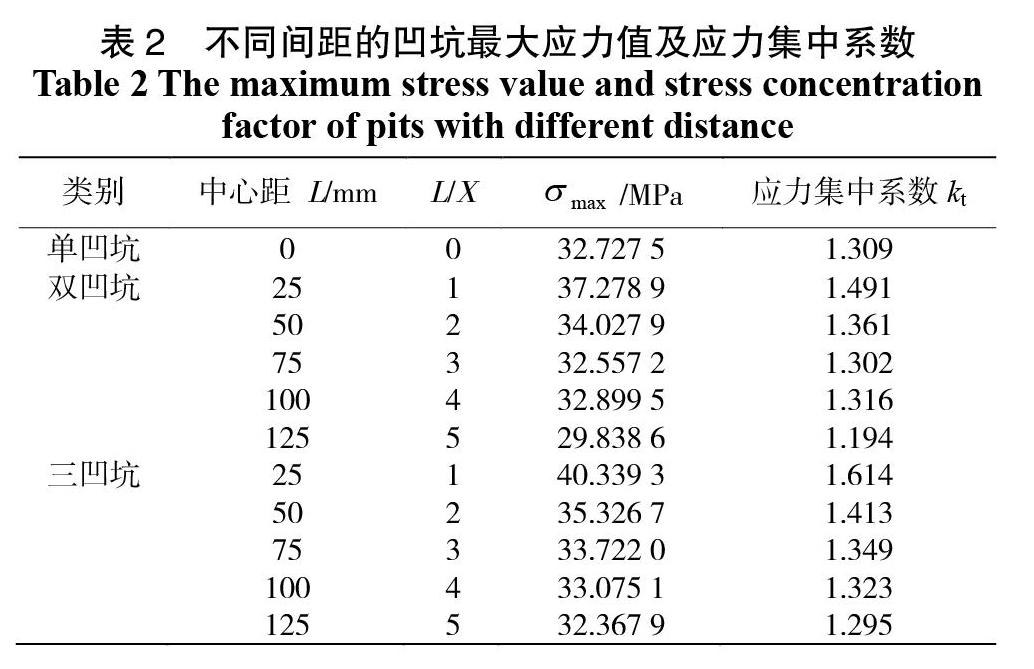
對于受恒壓的發酵罐體而言，其名義正應力為 ，為沒有缺陷時所對應的最大環向應力。從而可計算出應力集中系數，計算結果匯總如表2所示。

從表2可得出，當凹坑之間的中心距在L/X=1時其應力達到最大值，之后隨著相鄰凹坑中心距的增加其應力和應力集中系數也隨之降低，當中心距達到一定程度（L/X≥3.0）時，軸向排列的多凹坑，無論是雙凹坑還是三凹坑，其最大應力和應力集中系數受相鄰兩凹坑之間的距離影響并不明顯。此外，從圖5中可以看出，單凹坑的最大應力值和應力集中系數與雙凹坑和三凹坑相比最小，即最大應力值和應力集中系數與凹坑數量成正比。

無論相鄰凹坑距離多少，三凹坑的應力集中系數始終大于同一距離條件下的應力集中系數^[15]，說明凹坑缺陷的數量對發酵罐的應力分布及壽命有很大影響。

4 ?結 論

（1）凹坑缺陷的存在會導致局部應力集中現象，產生峰值應力，使發酵罐的安全運行受到威脅。通過對含有凹坑缺陷的罐體進行安全性評定可知，雖然罐體存在這些凹坑缺陷，但設計壓力始終小于最高容許壓力，即罐體處于安全狀態;但需注意的是罐體若長期在交變載荷的作用下，容易造成罐體疲勞破壞，應引起足夠重視。

（2）軸向排列的凹坑，如果相鄰凹坑的間距達到某一數值（L/X≥3.0）時，對應力分布的影響并不大;同時，應力集中系數隨著兩凹坑中心距的增加而減小，當間距L/X<3時其變化幅度較大，而L/X≥3后趨于恒定。

（3）最大應力值和應力集中系數與凹坑缺陷的數量成正比，而與相鄰的凹坑間距成反比，即凹坑數量越多其最大應力和應力集中系數越大，而隨著相鄰兩凹坑的間距增加，其最大應力值和應力集中系數降低。

參考文獻：

[1]紀曉懿，金長義.含凹坑缺陷的薄壁圓筒形壓力容器疲勞壽命數值模擬研究[J].化工技術與開發，2008，37（7）：42-45.

[2]張翼.邊緣應力區局部減薄強度特征的研究[D].天津大學，2006.

[3]趙菊.壓力容器蝕坑群干涉效應及安全評價[D].遼寧石油化工大學，2010.

[4]帥健，于桂杰.管道及儲罐強度設計[M].北京：石油工業出版社，2006.

[5]任國棟，周吉軍.在用含凹坑缺陷的壓力容器合于使用評價[J].化學工程與裝備，2016，（7）：148-149.

[6]徐尊平，雷斌隆.含弧坑缺陷壓力鋼管的安全評定[J]電焊機，2006，36（8）：53-54.

[7]紀曉懿.含凹坑缺陷薄壁圓筒形壓力容器的安全評定以及疲勞壽命的數值模擬研究[D].廣西大學，2008.

[8]陳亮.在役加氫反應器微試樣現場取樣可行性研究[D].華東理工大學，2015

[9]吳運祥，朱其康，徐宏.壓力管道表面腐蝕凹坑的安全評定與剩余壽命評估[J].金山油化纖，1998，（1）： 43-47.

[10]ANSI/ASME B31.Manual for Determing the Remaining Strength of Corroded Pipeline[S].1991.

[11]余偉煒，高炳軍.ANSYS在機械與化工裝備中的應用[M]. 北京：中國水利水電出版社，2006.

[12]符方杰，樊建春，張繼信.腐蝕缺陷對高壓管匯剩余強度的影響分析[J].石油機械，2012，40（6）：66-69.

[13]高宇，王茂廷，林國慶.基于ANSYS的壓力容器表面雙凹坑干涉效應分析[J].當代化工，2011，40（9）：975-977.

[14]梁瑞，張新燕，李淑欣，等.?半橢球蝕坑對圓棒應力集中的影響[J].中國腐蝕與防護學報，2013，33（6）：532-536.

[15]趙菊，王茂廷，梁浩騫.壓力容器多凹坑干涉效應分析[J].化工機械，2009，36（6）：579-581.