基于點擴散函數的黏聲介質反演成像

王雪君,任浩然,江金生,李瀚野

(浙江大學地球科學學院,浙江杭州310027)

吸收衰減是地球介質的一種基本屬性。面對復雜山前帶地震成像中小尺度油氣藏、深層油氣藏以及非常規油氣藏勘探,高分辨率地震成像越來越成為業界關注的焦點。對于高分辨率成像,地層的吸收衰減效應是一個重要的影響因素。有效的地震波吸收與衰減補償是地震資料處理工作的一個重要環節。

地層的黏滯性會導致地震波傳播過程中振幅衰減和相位變化,傳統的聲波逆時偏移和最小二乘逆時偏移不能對其進行校正,從而導致地下反射體能量不能得到有效的聚焦和歸位。品質因子Q描述了介質的吸收衰減特性,在地震勘探頻譜范圍內通常使用常Q衰減模型[1],在此模型基礎上發展了很多黏滯聲波方程。在過去的20年中,許多研究使用了頻率域單程波方程來補償上、下行波的衰減和頻散效應[2-7]。這些方法通常將衰減項放在復相速度虛部,以便實現反向補償。與頻率域黏滯聲波方程相比,時間域黏滯聲波方程具有更高的計算效率。ZHU等[8-9]提出了一種吸收衰減介質的時間域黏彈性波動方程,描述了常Q吸收衰減介質中的地震波傳播,且衰減和頻散運算符在這個方程中能夠被分離,從而通過反轉振幅算符符號而頻散算符符號不變來補償振幅衰減和相位頻散[10]。ZHU等[11]提出了基于時間域黏彈性波動方程及其反向傳播(時間反向)建模的黏彈性逆時偏移,在黏彈性波動方程中解耦P波和S波的衰減特性,從而在波場外推期間補償P波和S波的衰減效應,且設計了一種黏彈性逆時傳播方法,通過反轉P波和S波振幅損失算子的符號,來校正P波和S波的衰減效應。基于各向同性黏彈性公式,ZHU[12]將各向同性公式擴展到一般的各向異性黏彈性波動方程來模擬各向異性衰減介質,且推導出了時間域位移-應力公式。

基于牛頓法的全波形反演方法和基于線性化的高斯-牛頓法的最小二乘偏移方法都需要求解Hessian核函數。Hessian核函數在數學上是反問題泛函對模型參數的二階導數。而在物理學上,Hessian核函數疊合了地震波場正傳播和算子反傳播的所有信息[13]。Hessian核函數的敏感性更加能夠體現對地下成像空間每個點的照明響應,研究Hessian核函數對理解地震波場正、反演過程有著重要意義。在地震反演的研究中,Hessian算子有多種稱謂,如SCHUSTER等[14]提出的偏移格林函數、BOSCHI[15]提出的模型分辨率矩陣、FICHTNER等[16]提出的點傳播矩陣、XIE等[17]提出的照明矩陣、YU等[18]提出的去模糊化算子、WANG等[19]提出的偏移反褶積算子。這些概念都是Hessian算子的各種變稱。在局部線性化情況下,Hessian核函數又可以寫為線性的Hessian矩陣,當一個Hessian矩陣作用于最小二乘成像,會使得成像結果模糊,因此常規疊前偏移成像實際上是模糊的、振幅畸變的成像結果。點擴散函數(Point Spreading Function,PSF)是Hessian矩陣的一行,對應于地下一個成像點,反映了觀測系統對該點的照明能力。通常,PSF體現為目標點周圍的一個橢圓。反演理論證明,常規偏移成像結果就是該函數對理論成像結果的“模糊化”[20]。CHEN等[21]利用一個去模糊化算子來實現黏聲介質的最小二乘逆時偏移。研究帶Q因子的Hessian核函數,找出其在不同模型下的特征規律,解決Hessian矩陣的求解與求逆問題,是發展更高精度更高分辨率地震反演成像方法的理論基礎,可以為地球內部結構研究與油氣勘探提供更有利的成像工具。Hessian核函數的求解及求逆策略可以通過Hessian點響應矩陣的求逆來開展。因此,研究PSF,發展帶Q因子的PSF的求逆策略,可以將其逆算子直接作用在成像結果上從而提高成像分辨率。

本文是在ZHU等[8-10]和羅文山等[22]的研究基礎上,利用常Q模型吸收衰減與補償統一表達的一階“速度-壓力”黏聲波方程實現黏聲介質地震波場的格林函數計算,對Hessian矩陣分解與求逆方法進行研究,基于構建去模糊化算子,開展點擴散函數的逆矩陣研究,將逆Hessian點響應作用在成像結果上,從而對原始成像結果有效地去模糊化,提高了成像振幅均衡性和分辨率。最后用模型數據對方法的有效性進行了測試。

1 方法原理

1.1 黏聲介質地震波格林函數

有效的地震波吸收與衰減補償首先要解決的問題是如何有效描述地震波吸收與衰減的過程。地震波場的互易性理論揭示,地震波場傳播的正、反過程可以統一利用格林函數來表達,因此一個合理的、帶吸收衰減效應的格林函數表達式是進行反演理論框架下的地震成像的基礎。

1.1.1 黏聲介質地震波波動方程

吸收衰減介質中的應力-應變關系為:

(1)

式中:σ為應力;ε為應變;p為壓力;ψ1-2γ(t)為弛豫時間函數。且:

(2)

式中:M0和t0分別為弛豫體積模量和弛豫時間常數;Γ是歐拉γ函數;γ與Q有關;ρ,c0,Q分別為密度、參考角頻率ω0對應的速度和地震品質因子。

基于ZHANG等[5]推導的時間域黏聲波動方程,可以寫出吸收衰減介質地震波場衰減與補償的統一公式:

(3)

其中,

當α=1時,公式(3)為衰減公式;α=-1時,公式(3)為補償公式[10]。(3)式的一階速度-壓力形式為:

(4)

其中,u=?p/?t,vx=?p/?x,vz=?p/?z。當Q趨向無窮大時,γ→0,η→-1,τ→0,則(4)式退化為一階速度-壓力形式的純聲波方程。

1.1.2 數值計算方法

采用交錯網格有限差分進行波場模擬,對于(4)式中的高階項采用偽譜法進行計算。其公式為:

(5)

波場傳播到計算區域的邊界,采用最佳匹配層(PML)吸收邊界條件。由于PML是在非吸收衰減方程中得到的邊界條件,本質上也是對波場振幅的衰減。為了避免兩種衰減效應剛性過渡造成的邊界反射,在計算區與PML之間添加一個過渡區,在過渡區中兩種吸收衰減線性過渡。

1.2 Hessian核函數的求解與求逆

1.2.1 點擴散函數與其逆函數的求取

在背景介質中,記炮點位置為xs,檢波點位置為xr,由炮點傳播到散射點的頻率域格林函數定義為:

(6)

式中:σ(x)=1/v(x),為介質點xs上的慢度,v(x)為介質點集合x上的速度。類似的可以定義由檢波點到散射點的格林函數。在Born近似下,觀測系統的地震記錄可以表示為:

(7)

式中:fs(ω)為炮點xs處激發的能量在圓頻率ω上的譜;r是一個與反射系數相關的量。用矩陣-向量記法,(7)式可寫為:

(8)

式中:L表示一個線性模擬算子,與觀測系統、震源子波和地下介質模型參數有關;m0是地下反射率模型。對應正演模擬算子L,可以獲得其伴隨偏移算子LT,則偏移成像結果m可表示為:

(9)

(9)式用格林函數表示為:

(10)

式中:Gt表示G的共軛函數;m(x0)為位于x0處的點散射體;Ha(x,y)為Hessian算子,其表達式為:

(11)

可以看出,Hessian矩陣的元素Ha(x,y)對應兩組成像點,分別為x和y。Hessian矩陣的線性項表達成了格林函數的函數。而線性Hessian矩陣的每一個元素對應地下的兩個成像點,即線性Hessian矩陣的元素個數為成像點個數的平方,這個數量再加上矩陣求逆運算,計算量巨大。Hessian核函數的敏感性能夠更加體現在對地下成像空間每個點的照明。抽取線性Hessian矩陣的一行,即點擴散函數:

(12)

(12)式描述了對應于一個成像點x處的點擴散函數,可以看到單點的PSF彌散到整個成像空間的所有點y,反映了觀測系統對該點的照明能力。正向傳播的兩個格林函數G(xs,x,ω)和G(x,xr,ω)描述了地震波場從震源傳播到點x處經由散射傳播到接收點的過程;而反向傳播(共軛即是反向傳播)的兩個格林函數Gt(xs,y,ω)和Gt(y,xr,ω)描述了地震波場從接收點反傳到y處經由散射反傳到震源點的過程。而整個正傳、反傳的過程恰好反映了地震波在背景介質中傳播對于散射點的聚焦程度。

針對單個散射體來說,其點擴散函數響應即為其偏移成像結果。GUITTON[23]提出了一種局部去模糊濾波器構建方法,直接在空間域執行去模糊偏移成像。給定參考模型m0,觀測數據uobs,可得到常規偏移成像結果m1:

(13)

對該結果進行反偏移,得到新數據:

(14)

對新數據u1再次進行成像,獲得新的偏移結果m2:

(15)

其中,兩次成像結果之間的關系為:

(16)

也就是說,m2是m1經過Hessian算子模糊作用后的成像結果。

假設采用一組非平穩濾波器來解決以下優化問題:

(17)

則B就是(LTL)-1的一個最優化估計。將估計得到的B作用到成像結果m1上,得到去模糊化的成像結果。

1.2.2 解析表達的PSF

聲學格林函數可以表示為如下解析表達式:

(18)

如果為黏性介質,則將完全彈性介質中的實速度v0替換成復速度v(ω):

(19)

從而得到黏聲介質的格林函數:

(20)

其中,ξ={1+(1/πQ)[ln(ω/ω0)]}[1+(1/4Q2)]。因此,可據此給出聲學和黏聲情況下的PSF:

(21)

利用與聲介質情況相同的去模糊濾波器來求取黏聲介質點擴散函數的逆,然后作用于常規偏移成像結果上就能達到去模糊化的效果。

2 模型參數實驗

2.1 黏聲介質復雜模型逆時偏移成像測試

針對簡單模型的逆時偏移我們設計了一個凹陷速度模型,如圖1所示,模型大小為1500m×2000m,水平、垂直網格間距都是5m。速度范圍為3500～5000m/s。

圖1 凹陷速度模型

首先,我們設Q值為常數,分別對該模型整體設置Q=5,10,30,100和無窮大,圖2為不同Q值對應的地震記錄。由圖2可以看出,Q值的變化會造成不同程度的振幅衰減,且Q值越小衰減越嚴重。從圖2還可以看出,由于Q值的影響,地震記錄有向下的時移,這表明Q值對地震波傳播具有相位畸變效應。圖3給出了不同Q值下的同一單道地震記錄。從圖3 可以看出,Q值除了引起振幅的衰減,還使得相位發生了變化:Q越小相位越滯后。

圖2 不同Q值對應的地震記錄

圖3 不同Q值的同一單道地震記錄

考慮地質構造特征,我們重新設置Q值,使得Q值結構與速度模型結構相對應,模型的Q值設置如圖4所示。模擬100炮地震數據,炮點位置從450m開始,炮間距為15m。地表位置布滿接收點,總道數為400道,道間距5m,記錄長度0.88s,時間采樣率1ms。

圖5給出了采用不同數據和成像方法得到的成像結果。

圖4 凹陷Q模型

圖5a為聲介質成像結果;圖5b為正演的衰減數據不加以補償的逆時成像結果;圖5c為正演的衰減數據給予補償的逆時成像結果。由圖5可以看出,與聲介質成像結果相比,偏移時如果不對衰減數據進行Q補償,地震波能量明顯減弱,圖像分辨率變低,衰減層越到下方成像效果越差,圖像層位也不準確,層位略向上移動。當采用本文衰減與補償統一表達的黏聲介質傳播方程對帶吸收衰減數據進行補償成像后,成像結果的振幅得到補償,下方層位被有效地恢復出來,圖像層位也準確。該實驗結果證明了吸收與衰減統一表達的黏聲介質波動方程能夠有效地計算黏聲介質地震波場的格林函數。

2.2 黏聲介質PSF特性分析

圖6為鹽丘速度模型,模型大小為6000m×750m,水平、垂直網格間距都是5m。考慮常規地質構造中,Q值結構與速度模型結構相對應,我們設置模型中的Q值分布如圖7所示。模擬325炮數據,炮間距15m。中間放炮,兩邊接收,每一炮覆蓋總道數為200道,道間距5m,記錄長度2.5s,時間采樣率0.3ms。用數值實驗來觀測線性Hessian矩陣的單點響應。

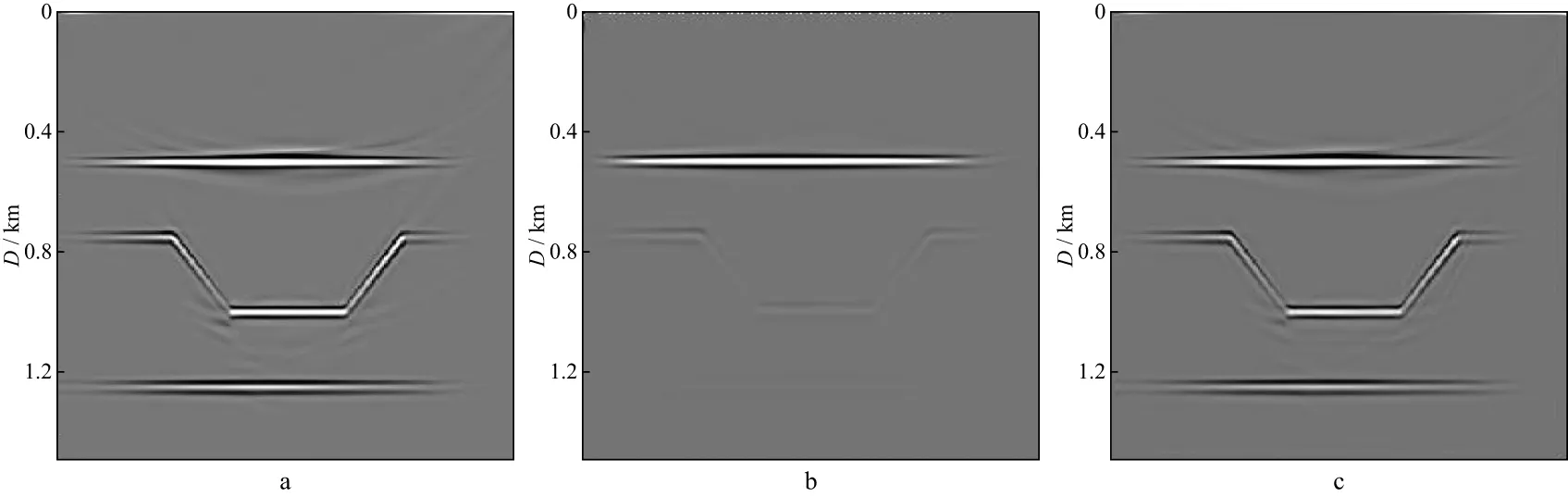
圖5 不同數據和成像方法得到的成像結果a 聲介質成像結果; b 正演的衰減數據不加以補償的逆時成像結果; c 正演的衰減數據給予補償的逆時成像結果

按照模型數據的觀測系統和頻帶分布,我們根據公式(21)計算其點擴散函數。將模型劃分為231個網格大小為21×21的區域,目標點位于網格區域中心。圖8給出了圖6中6個參考點的點擴散函數圖(1～6號參考點的中心坐標分別為:[436,10],[562,31],[751,31],[457,73],[667,73],[688,94])。從圖8中可以看出,點擴散函數集中在中心點周圍區域。在這一區域之外,單點響應相對區域內為極小值。另外,由于淺層速度結構簡單,同時照明也較為均勻,它們的PSF也是簡單的橢圓形。而在速度變化劇烈的區域,PSF卻是畸變的,而且具有一定的方向特性。對比圖8中聲介質單點PSF與黏聲介質PSF可以發現:吸收衰減效應顯著降低了照明振幅強度,帶吸收衰減的PSF明顯比聲介質PSF能量低,在深層這種能量損耗更為強烈;吸收衰減效應改變了觀測系統對地下的照明圖樣,即各點在兩種情況下的分辨率相差較大。

在中心點位置將PSF圖樣按照空間位置進行排列,將全觀測系統的PSF圖樣顯示在圖9(聲介質)和圖10(黏聲介質)中。

圖6 SEG/EAGE鹽丘模型

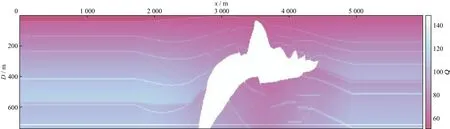
圖7 鹽丘Q模型

從圖9和圖10可以看出,吸收衰減效應的影響體現在全空間中,其顯著降低了鹽丘下方照明振幅。也可以看到,線性Hessian矩陣在不同區域展示的單點響應不同。淺層速度結構簡單,同時照明也較為均勻,它們的PSF是簡單的橢圓形;而在速度變化劇烈的區域PSF發生了畸變,且有一定的方向特性,圖樣更為分散;在鹽丘周圍,吸收衰減效應顯著降低了成像分辨能力。

2.3 基于點擴散函數的反演測試

圖11和圖12分別給出了聲介質和黏聲介質的逆PSF成像結果。圖13給出了常規聲介質偏移成像結果。雖然沒有Q的影響,但在高速體下方,常規偏移成像并不能得到顯著的層位信息。圖14給出了逆PSF作用在常規聲介質偏移成像結果后的成像結果。可以看出,逆PSF作用在常規聲介質偏移成像結果上,能夠達到去模糊的作用,特別是在鹽丘下方,能夠有效恢復層位信息。

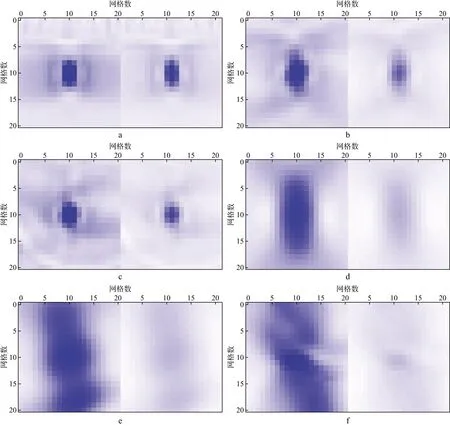
圖8 圖6中6個參考點的PSF分布(左邊為聲介質的PSF分布,右邊為黏聲介質的PSF分布)a 參考點1; b 參考點2; c 參考點3; d 參考點4; e 參考點5; f 參考點6

圖9 全觀測系統點擴散函數分布(聲介質)

圖10 全觀測系統點擴散函數分布(黏聲介質)

圖15給出了采用黏聲數據并加以補償的常規偏移成像結果。由圖15可以看出,衰減層及其下部反射體的成像振幅逐漸減弱,成像分辨率逐漸降低。圖16給出了逆PSF作用在圖15 成像結果后的成像結果。對比圖15和圖16可以看出,逆PSF顯著增強了深層成像的能量,成像剖面振幅更加均衡,吸收衰減效應能夠通過逆PSF進行有效補償。

圖11 聲介質逆PSF成像結果

圖12 黏聲介質逆PSF成像結果

圖13 直接偏移成像結果(聲波數據+聲波成像)

圖14 逆點擴散函數作用后的成像結果(聲波數據+聲波成像+聲波PSF)

圖15 直接偏移成像結果(黏聲數據+黏聲成像)

圖16 逆點擴散函數作用后成像結果(黏聲數據+黏聲成像+黏聲PSF)

3 結論

本文從衰減與補償統一表達的黏聲介質傳播方程出發,利用交錯網格有限差分方法和最佳匹配層吸收邊界條件進行求解,實現了黏聲介質衰減與補償的格林函數計算。基于地震反演成像理論和數值實驗結果,對點擴散函數的敏感性以及Q因子對點擴散函數數學、物理特征的影響進行了分析。結果表明,PSF反映了吸收衰減效應對波場穿透能力和角度照明能力的影響。利用去模糊濾波器對PSF進行求逆,并將逆點擴散函數直接作用在成像結果上,從而對原始成像結果有效地去模糊化,并提高成像振幅的分辨率和均衡性。模型數據實驗結果證明了該方法的有效性,在黏聲介質中的逆時偏移成像可以達到與聲介質成像相當的精度。基于這一系列研究成果,可以進一步開展迭代的最小二乘偏移成像和全波形反演方法研究。

致謝:感謝同濟大學海洋與地球科學學院波現象與反演成像研究組(WPI)對本研究工作的幫助。