基于FPGA的電阻爐模糊控制器設計

文/張佳 代小宇 顧建軍

電阻爐是在我國應用較廣的一種被控對象，其溫度變化非線性，難以精確建模，優化這樣的系統控制性能是大多數工程師所需要解決的問題。傳統PID控制主要適用于線性控制對象，在控制這類對象時可能會出現難以控制的現象。而模糊控制是依據操控人員的經驗，通過查表來得到控制量，更加智能化。本文將以電阻爐溫控系統為引導，主要研究其核心控制器的原理及具體實現。

1 電阻爐的數學模型

電阻爐裝置是一個閉環反饋控制系統，是具有自平衡能力的對象，可用二階慣性和滯后環節來近似描述，而通過參數辨識可以將二階不振蕩系統降為一階模型，則電阻爐溫度控制系統模型的傳遞函數可以表示為：

式中K為放大系數，τ0為純滯后時間，T為時間系數。在現實的控制中，因需要考慮到種種因素，使得上述數學模型與實際非常不符，因此選用PID算法與模糊控制結合的方式對本系統進行設計。

2 電加熱爐的模糊自整定PID算法

模糊自整定PID控制基于PID算法，通過計算當前系統設定值與反饋值之間的誤差e和誤差變化率ec，在控制過程中實時計算e和ec，找出其與Kp，Ki，Kd之間的模糊關系，并查詢模糊規則表實時地輸出對應的控制量。本文用FPGA技術實現設計，需要進行離散化處理，離散的PID表達形式如下：

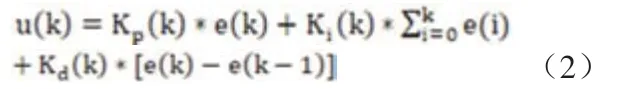
上式的計算可以很方便的利用FPGA中的函數模塊實現，相比于原PID公式大大減輕了計算量，加快了運算速度，提高了系統性能。

3 模糊PID算法的FPGA的實現

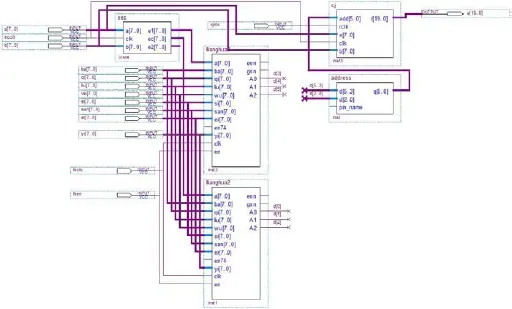
圖1：頂層電路圖

除其靈活性、高集成、低功耗的優點，本文用FPGA來實現核心控制器部分，還避免了不必要的硬件開銷，提高了系統的運行速度和可靠性。設計可分為4個模塊:誤差及誤差變化量產生模塊、模糊量化模塊、查找表模塊以及乘加模塊。

3.1 誤差及誤差變化量模塊的設計

本模塊輸入為設定值與反饋值，輸出為其誤差及誤差變化量。利用QuartusII軟件中自帶的LPM_ ADD_ SUB函數即可實現該模塊。

3.2 量化模塊的設計

量化模塊的基本思路是：首先將基本論域分為若干段，每一段對應于一個語言值，確定輸入的精確值落入哪一段，此段對應的語言值即為此精確量的量化值。利用QuartusII里自帶的LPM_ COMPARE函數模塊以及編碼器完成設計。

3.3 模糊查找表模塊

本文的模糊查找表用MATLAB離線生成，通過自帶的模糊邏輯工具箱，可以自定義設置隸屬度函數、建立模糊規則等來建立并測試模糊邏輯系統，利用仿真功能建立該系統模型，輸入所有e和ec的不同組合到該模型中求出不同情況下PID三個參數的值。

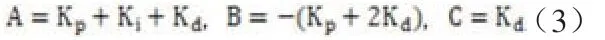
設置三個變量A,B,C如下：將A, B, C與e和ec進行特定的乘加運算，即可等價為式（2），由此將計算更加簡化。在Quartus II里用ROM模塊來存放查找表，e與ec的量化地址作為ROM的輸入。

3.4 乘法模塊和加法模塊

調用QuartusII里自帶的lpm_mult及parallel_ add函數模塊完成下式的運算：

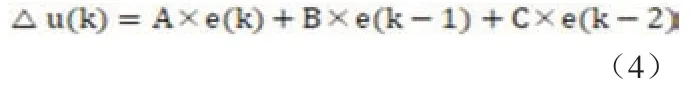
得到最終的控制量△u。

3.5 系統頂層電路原理圖

如圖1所示。

4 結束

本文基于FPGA技術設計了模糊自整定PID控制器實現對電阻爐溫控系統的控制，設計采用線下生成查找表，實時查表計算的模糊自整定PID算法，并在QuartusII軟件上利用原理圖設計方法完成設計并且仿真，據仿真結果顯示，此設計方案可行。