讓人糾結的箱子

劉金龍

塔塔鎮來了一位奇怪的魔法師，他在鎮子東頭的老槐樹下放了兩個箱子，說要和鎮上的居民們玩“選箱子”的游戲。他的舉動引來了鎮上的人圍觀。

魔法師的游戲

魔法師擺放的兩個箱子，其中甲箱子是透明的，里面有一枚黃燦燦的金幣，而乙箱子是不透明的，里面可能什么都沒有，也可能會有一根魔杖。這根魔杖可是很厲害的，可以實現一些愿望，當然了，使用者必須是本著善良的初心。

一切準備妥當，游戲開始了——

參與者有兩種選擇：一種選擇是拿走兩個箱子，但當魔法師預測到你會這樣做時，他會讓乙箱子空著；另一種選擇是只拿走乙箱子，當魔法師預測到你會這樣做時，他會提前將一根魔杖放進乙箱子。注意，選擇的機會只有一次，請慎重考慮。

聽完游戲規則，大家便你一言我一語地商量了起來。

“當然是兩個箱子都拿走了，至少能得到一枚金幣。”

“金幣我可不稀罕，我想要魔杖，我只拿乙箱子。”

“只拿乙箱子，如果魔法師預測錯誤，你將什么都得不到。”

“就是！最好是拿兩個箱子。如果魔法師預測錯誤，我就能得到一枚金幣和一根魔杖。”

“噓！大家別著急，既然是魔法師擺放的箱子，哪會那么容易讓我們都拿走。我從隔壁鎮親戚那里聽到一個關于魔法師的秘密，他有預測未知的魔力，據說準確率高達90%。”

…………

塔塔鎮的居民們在熱烈地討論著，你也別在一旁看熱鬧。如果你也是游戲的參與者，你會做出何種選擇呢？

我也覺得將兩個箱子都拿走是比較明智的選擇，萬一魔法師的預測不準，我還能拿到一枚金幣和一根魔杖。

可魔法師預測的準確率高達90%，這個概率很高啊！不過終究不是100%，還是會出現預測錯誤的可能。

不同選擇，不同說法

一番討論后，很快，塔塔鎮的居民們就分成了兩撥，因為他們考慮這個問題用了不同的思維方式。

“如果魔法師預測拿箱子的人會將兩個箱子都拿走，他就會讓乙箱子空著。這時候，拿箱子的人就應該將兩個箱子都拿走，這樣至少能得到一枚金幣。如果魔法師預測拿箱子的人只拿乙箱子，他就會將一根魔杖放入乙箱子。這時候，拿箱子的人更應該將兩個箱子都拿走，因為甲箱子里可是有一枚金幣呢，它鐵定是存在的，沒理由放著不要啊！”其中一方代表發了言。

“對，沒錯！”其他人紛紛附和道。

“反對！”

“反對！”

“魔法師有預測未知的能力，預測的準確率高達90%，那么只拿乙箱子，會有90%的概率能得到一根魔杖。但是如果將兩個箱子都拿走，就只有10%的概率能得到一根魔杖和一枚金幣。所以，只拿走乙箱子才有最大可能得到一根魔杖。”另一方代表反駁道。

他們的分析都很有道理，到底該拿兩個箱子還是只拿乙箱子呢？

又犯迷糊了吧！這就是魔法師的精妙之處，也是數學的有趣之處，繼續認真往下看吧。

不管怎么選，矛盾總會出現

對于塔塔鎮的居民們來說，無論哪一種選擇，他們都想收益最大化。對于他們的選擇，我們沒辦法評判誰對誰錯。不過，既然知道了魔法師預測的準確率，那么我們不妨試著用概率知識來分析一下。

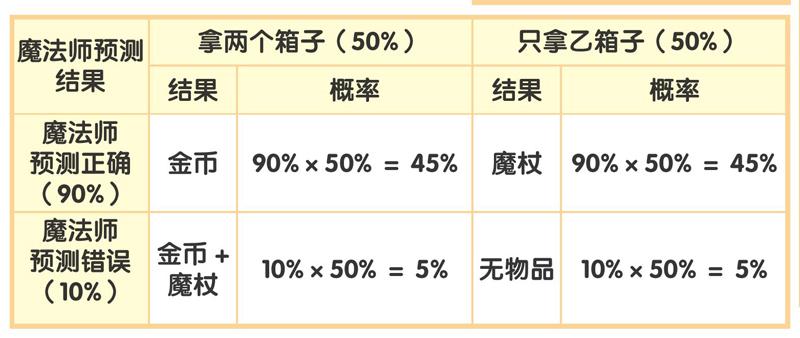
當魔法師預測正確時，最好的結果是拿箱子的人得到一根魔杖。而當魔法師預測錯誤時，最好的結果便是拿箱子的人得到一枚金幣和一根魔杖。

當選擇拿走兩個箱子時，可能會出現兩種結果：得到一枚金幣或者得到一枚金幣和一根魔杖。當選擇只拿走乙箱子時，也可能會出現兩種結果：得到一根魔杖或者什么也沒得到。因為選擇拿走兩個箱子和選擇只拿走乙箱子是兩個相互獨立的事件，所以，這兩種選擇發生的可能性都是50%。

選擇拿走兩個箱子時，能得到一枚金幣的概率是100%，而能得到一根魔杖的概率卻只有10%。從整體分析，選擇拿走兩個箱子的概率是50%，所以，能得到一枚金幣和一根魔杖的概率就是5%，而能得到一枚金幣的概率是45%+5%=50%。

選擇只拿走乙箱子時，能得到一根魔杖的概率是90%，什么都得不到的概率是10%。從整體分析，選擇只拿走乙箱子的概率是50%，所以，能得到一根魔杖的概率是45%，而什么都得不到的概率是5%。

根據上述表格數據，如果想獲得魔杖，那么我們應該選擇只拿走乙箱子，不過放棄了本可以拿到的金幣，這與“收益最大化”矛盾；如果拿走兩個箱子，魔法師高達90%的預測準確率擺在那兒，也與“收益最大化”矛盾。不管怎么選擇，矛盾總會出現，這就是著名的“紐康姆悖論”。

唉，忙活了半天，原來是無解啊！

從分析過程來看，這一切都與魔法師預測的準確率有關。我們不妨試著改變一下這個準確率，看看情況會怎么樣。

改變準確率，情況大不同

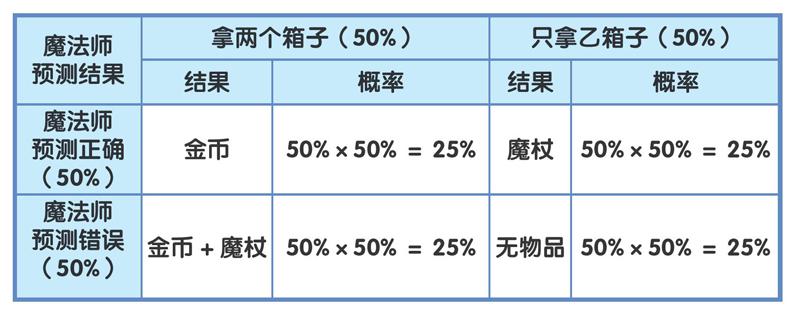
假設將魔法師預測的準確率改為50%，那么選擇拿走兩個箱子時，能得到一枚金幣的概率是100%，而能得到一根魔杖的概率達到了50%。從整體分析，兩個事件發生的概率還是各占50%，所以，能得到一枚金幣和一根魔杖的概率是25%，而能得到一枚金幣的概率還是25%+25%=50%。

而選擇只拿走乙箱子時，能得到一根魔杖的概率降到了50%，什么都得不到的概率則上升到了50%。從整體分析，選擇只拿走乙箱子的概率為50%，從而得出拿到一根魔杖的概率降為25%，而什么都得不到的概率上升到25%。

這樣的話，毫無疑問，當然是將兩個箱子都拿走了，因為無論是否拿甲箱子，能得到一根魔杖的概率都是25%，而將兩個箱子都拿走還能得到一枚金幣。若不拿甲箱子，反而有25%的概率空手而歸。

看來，魔法師預測的準確率才是這個悖論的關鍵所在啊！

之所以為悖論，或許是因為本身給出的一些條件所限制，改變其中的關鍵條件，也許悖論就不存在了。