基于Sym小波與BP神經網絡的裝配柱鋼筋套筒灌漿連接缺陷檢測方法

韓 笑 唐和生 周德源

(同濟大學結構防災減災工程系,上海 200092)

0 引 言

隨著近年來建筑工業化的大力推行,裝配式建筑越來越多地出現在了我們的生活當中。裝配式建筑具有施工速度快、環境污染小、節約人力等優點,具有顯著的發展潛力。裝配式結構與現澆結構的主要區別在于節點的連接性能,若能保證節點良好的連接性能,裝配式結構完全可以代替現澆結構。有研究表明裝配整體式管框架結構的地震損傷程度與普通框架結構相比,并沒有明顯的差別,但裝配整體式框架結構的節點仍是其抗震中的薄弱環節[1]。裝配式框架結構廣泛用于商辦項目,多數的裝配式柱采用灌漿套筒與節點連接,其鋼筋連接性能與結構的承載能力與抗震耗能能力密切相關。故有必要研究一種無損檢測方法,以評估裝配柱鋼筋的連接性能。

結構構件的損傷會引起結構動力響應的變化,近年來,小波分析和BP神經網絡成為了損傷檢測的兩大強有力的工具。小波分析具有低熵性、多分辨率、去相關性、選基靈活性;BP神經網絡具有較強的容錯性、冗余性以及自我更新能力,且理論上可以映射任何非線性關系。本文結合兩種方法,對裝配柱灌漿套筒連接的損傷識別方法進行探究。

1 裝配式柱的數值模擬

1.1 計算模型

本文采用通用有限元軟件ABAQUS建立數值模型,模型的尺寸與構造參考相關規范[2-3]。裝配柱采用400 mm×400 mm矩形截面,柱高3 m,套筒連接長度為220 mm,軸壓比取0.5。混凝土標號為C40,縱筋及箍筋均采用HRB400級鋼筋。在激振方向上采用對稱配筋,兩端各配422,在非受力方向兩側各配腰筋220,箍筋選用8@100。在柱高中點處布置激振點,距柱底1/4高度處布置4個測點。具體尺寸配筋、縱向鋼筋編號以及測點布置位置如圖1所示。

在ABAQUS軟件建模中,裝配柱兩端固接,鋼材的密度取7 800 kg/m3,彈性模量取2.1×1011N/m2,泊松比取0.3;混凝土密度取2 500 kg/m3,彈性模量取3×1010N/m2,泊松比取0.2。混凝土采用三維實體縮減積分單元C3D8R,鋼筋采用二節點直線桁架單元T3D2;剛性加載板與混凝土柱之間采用Tie約束;鋼筋用Embedded方式植入混凝土中;模型采用振型模態法(取前50階模態)計算沖擊響應,采用模態阻尼,根據經驗,前10階模態阻尼取0.04,后40階模態阻尼取0.05。模型的邊界情況及網格劃分如圖2所示。

圖1 裝配柱截面詳圖(單位:mm)Fig.1 Detail of assembly column (Unit:mm)

圖2 裝配柱有限元模型Fig.2 Finite element model of assembly column

1.2 引入損傷

根據已有研究[4]可知,在裝配工程中,套筒灌漿接頭可能因氣泡、堵塞、漏漿等造成各種灌漿缺陷,主要的套筒灌漿缺陷類型如表1所示。

可以看出,表中的缺陷類型對套筒連接性能的影響主要表現為削弱了鋼筋與灌漿料的連接,將這些缺陷視為鋼筋套筒連接段的彈性模量折減(當套筒與鋼筋完全失去連接時,連接段彈性模量折減至0),將各編號鋼筋連接長度范圍內的彈性模量折減(由于套筒連接質量缺陷造成)作為數值模型中的損傷引入,按下式計算:

表1套筒灌漿缺陷類型

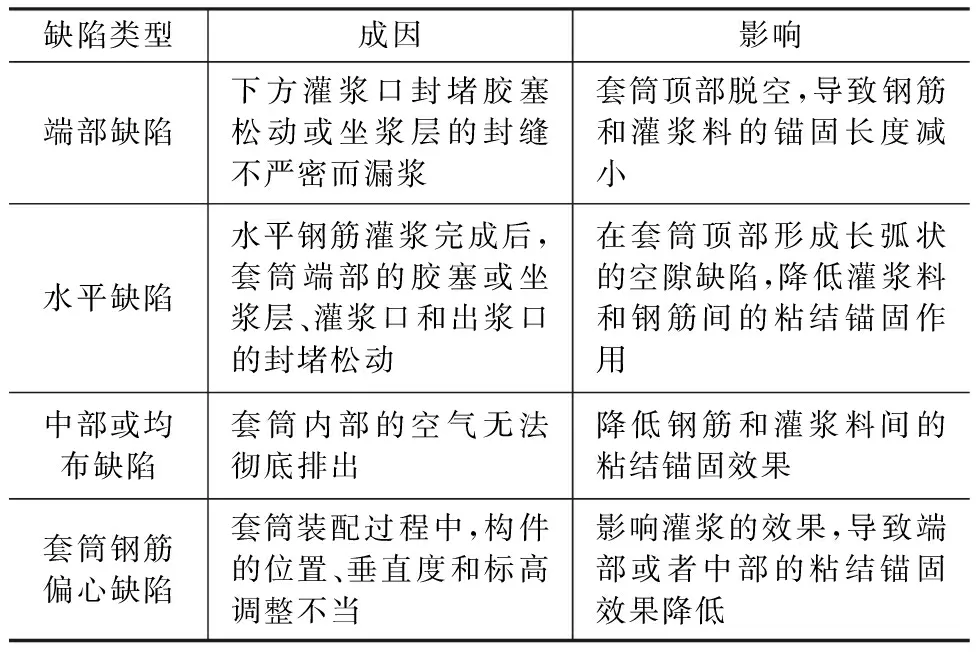
Table 1Type of sleeve grouting defect

(1)

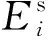
在后文中,以Di-di表示編號為i的鋼筋損傷di,如D1-0.7表示編號為1的鋼筋在連接段內彈性模量折減70%。

1.3 加載與數據采集

模擬檢測時的錘擊[5],在模型激振點處施加一個瞬態半波正弦沖擊力:

(2)

式中:P(t)為作用在激振點的一個瞬態半波正弦沖擊力;P0為沖擊波的幅值,取10 kN;T取為裝配柱的一階自振周期,經有限元軟件計算,約為6.5 ms。

在有限元模型中,每1 ms采集一次數據,總共采集時間為200 ms,以詳細地記錄模型的響應信息。

2 基于小波分解的能量特征值提取

2.1 小波變換

在計算機中,多采用二進制動態采樣網格,每個節點對應的尺度為2i,平移為2ik。根據此得到離散化小波函數[6-7]:

(3)

式中,i,k∈Z,ψi,k(t)稱為二進小波。

本文通過Matlab軟件來實現小波變換。

2.2 Sym8小波基

小波變換的一個關鍵點在于小波基的選取,因Symlets系列小波是有限緊支撐正交小波,其時域和頻域的局部化能力均較強,特別是在數字信號的處理中,可以提供有限長的更實際、更具體的數字濾波器[5],故本文采用Sym8小波作為小波變換的小波基。Sym8小波基的小波函數及尺度函數如圖3所示。

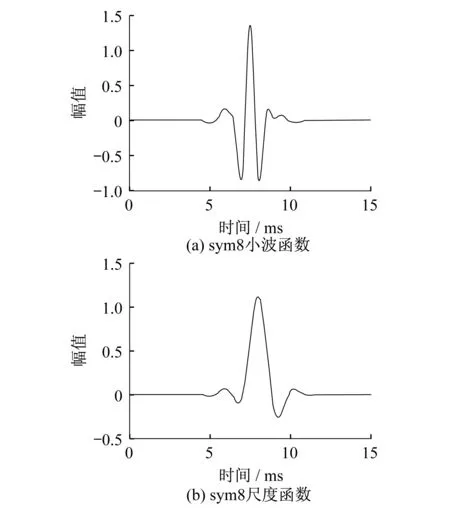
圖3 Sym8小波函數及尺度函數Fig.3 Sym8 wavelet function and scale function

2.3 能量特征值提取

將信號進行小波分解后,可以得到信號中若干頻帶成分的信息,當結構發生損傷時,因損傷對響應信號各頻帶成分的作用不同,可能抑制,也可能增強,從而導致各頻帶成分的相關參數重新分布[8],因此,帶損傷的裝配柱與未帶損傷的裝配柱相比,其響應信號中個頻帶所攜帶的能量占比也會發生改變,故提取能量占比變化顯著的分解層次所對應的能量變化百分比作為結構的特征值。

利用小波分析,將各測點所得到的加速度響應一維原始信號進行分解層次為8層的小波分解,以P1測點為例,未損傷時的各成分如圖4所示。圖中,S表示原始信號,d1到d8分別表示由高到低的第1層到第8層高頻分量,a8表示第8層低頻分量。

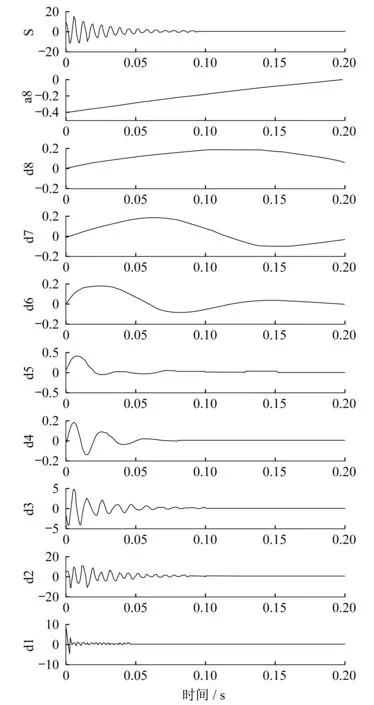
圖4 鋼筋未損傷時的加速度響應小波分析Fig.4 Wavelet analysis of acceleration response with undamaged reinforcements

將8層高頻分量與第8層低頻分量做能量統計。經過j-1層小波分解(含j-1個高頻分量,1個低頻分量),原始信號S(t)可以寫成[9]:

(4)

其中

(5)

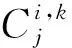
(6)

信號S(t)的總能量為

(7)

由小波基的性質可得

(8)

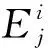
(9)

各頻帶能量占比變化量為

(10)

以P1測點所采集信號的能量占比變化量為例,對比幾種不同編號鋼筋不同損傷程度的工況,以選出對損傷敏感的分解層次。對比情況如圖5所示。

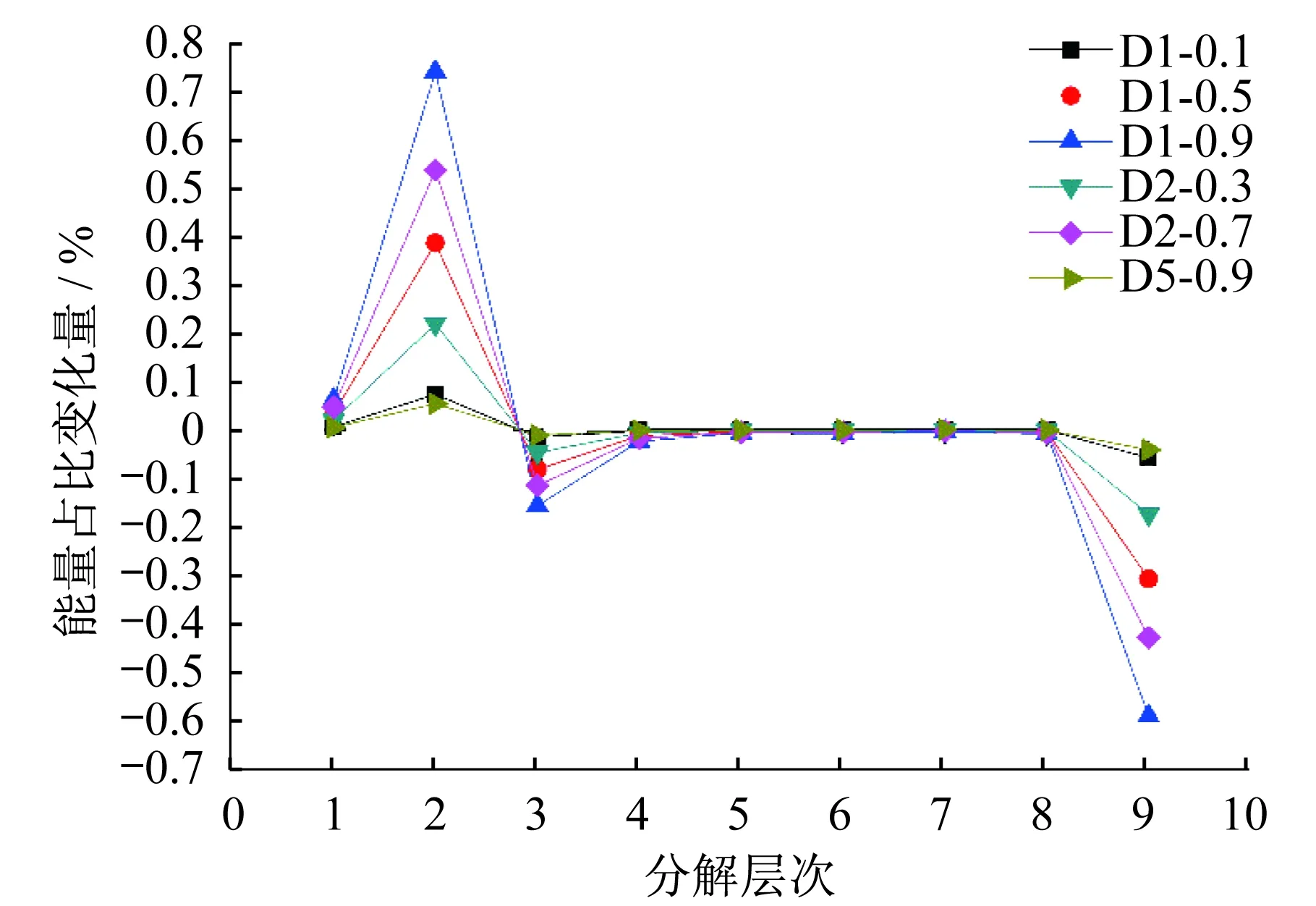
圖5 各分解層次能量占比變化量Fig.5 Change in energy ratio of each decomposition level

可以看出,分解層次為高頻成分d2,d3以及低頻成分a8(在圖5中分別對應1,2,9)的能量占比變化量對損傷最為敏感,對同一編號的鋼筋,損傷程度越大,ΔP2越大,ΔP3,ΔP9越小。故將ΔP2,ΔP3,ΔP9作為能量特征值。

3 基于BP神經網絡的缺陷識別

3.1 BP神經網絡關鍵參數選取

BP神經網絡具有強大的映射能力及自我更新特性[10],其基本原理是將誤差從輸出層向輸入層傳播,并沿途調整各層間的連接權值與閥值,使誤差不斷減小,直至達到合理的精度,以實現訓練網絡的目的。其誤差目標函數為

(11)

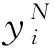
每次訓練所調整的第m-1層到第m層的權值增量Δw由下式計算:

(12)

式中,lr為學習速率,取0.01。

選擇非線性激勵函數tansig作為網絡的激勵函數,其表達式為

(13)

采用Levenberg-Marquardt(L-M)規則訓練網絡,可以很大程度減小網絡訓練時間[11];輸出層以線性函數purelin作為神經元的激勵函數,不僅減少平坦區現象,而且有利于消除非線性函數造成的畸變現象[12]。

神經網絡的訓練樣本與網絡拓撲之間并無確切的數量關系,常根據下式估計各參數值[13]:

(14)

式中:NP為訓練樣本數;h為隱含層節點數,本文采用54個樣本用以訓練網絡,輸入向量維數p為3,輸出向量維數q為1,故取h為12。

3.2 確定輸入與輸出參數

如2.3中所述,選取第2層、3層高階頻帶與第8層低階頻帶的能量占比變化量,在數值模型中,布置了4個測點(P1,P2,P3,P4),每個測點獲得的原始信號均能得到一組變化量,將四個測點的變化量取平均,作為神經網絡的輸入參數組{ΔP2,ΔP3,ΔP9}。

定義神經網絡的輸出參數分別為彈性損傷系數{ED}與塑性損傷系數{PD},兩者對應的神經網絡分別為Enet與Pnet。

當連接段鋼筋受到損傷時,連接段截面的剛度損失δEI為

(15)

則定義彈性損傷系數ED為

(16)

式中:δEi為第i根鋼筋的等效損傷彈性模量折減量;Ai為第i根鋼筋的面積;li為第i根鋼筋到彈性中和軸的距離。

對于塑性損傷系數,其與截面進入完全塑性狀態時中和軸的位置相關,本文中取裝配柱的軸壓比為0.5,其塑性損傷時的中和軸近似認為在截面高度中間(即在完全塑性階段往復荷載作用下,中和軸的位置不變),當連接段鋼筋受到損傷時,截面進入全塑性狀態時,連接段截面的抵抗矩損失δM為

(17)

則定義塑性損傷系數PD為

(18)

式中,ri為第i根鋼筋到塑性中和軸的距離。

3.3 網絡訓練生成

采用數值模擬得到的輸入輸出參數來訓練神經網絡,可以獲得大量的數量樣本,相較于實際模型而言,可以有極大地降低成本,并且可以覆蓋較大范圍的損傷情況與損傷程度[14]。用于訓練網絡的損傷工況如表2所示。

表2訓練樣本損傷引入情況

Table 2Damage introduction of training samples

對于識別彈性損傷的神經網絡Enet,選取隱層層數為1,其余參數如3.1中所述,訓練結果如圖6所示。

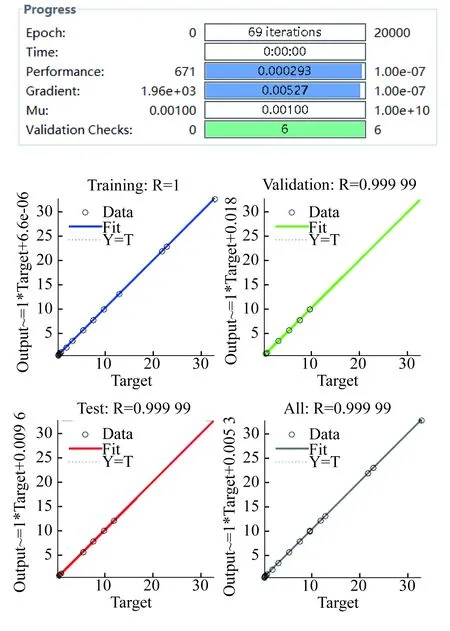
圖6 Enet訓練結果Fig.6 Enet training results

網絡訓練完成后,迭代總次數為69次,最終的均方差為0.000 293,最小梯度為0.005 27。Training (訓練)、Validation (驗證)、Test (測試)、All (總體)的相關系數R均十分接近1,說明訓練得到識別彈性損傷的神經網絡是滿足要求的。

對于識別塑性損傷的神經網絡Pnet,選取隱層層數為3,其余參數如3.1中所述,訓練結果如圖7所示。

網絡訓練完成后,迭代總次數為91次,最終的均方差為7.27×10-5,最小梯度為0.001 63。Training (訓練)、Validation (驗證)、Test (測試)、All (總體)的相關系數R也都十分接近與1,說明訓練得到的識別塑性損傷的神經網絡同樣是滿足要求的。

3.4 網絡識別能力測試

為了檢驗訓練得到的Enet與Pnet對彈性損傷與塑性損傷的識別效果,利用有限元軟件模擬多種損傷工況,用以檢驗網絡。損傷工況及檢驗結果如表3、表4所示。

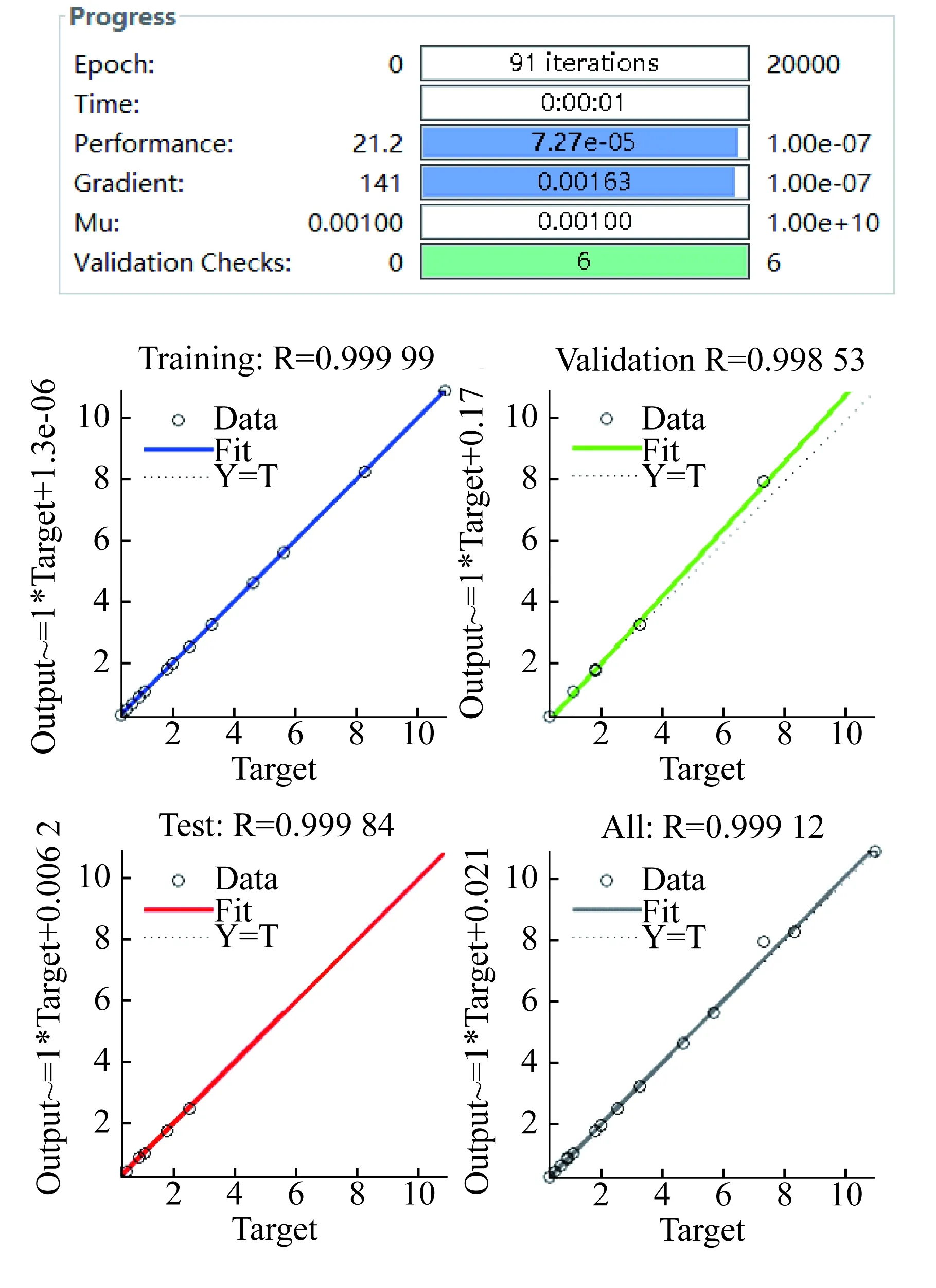
圖7 Pnet訓練結果Fig.7 Pnet training results

表3彈性損傷測試結果

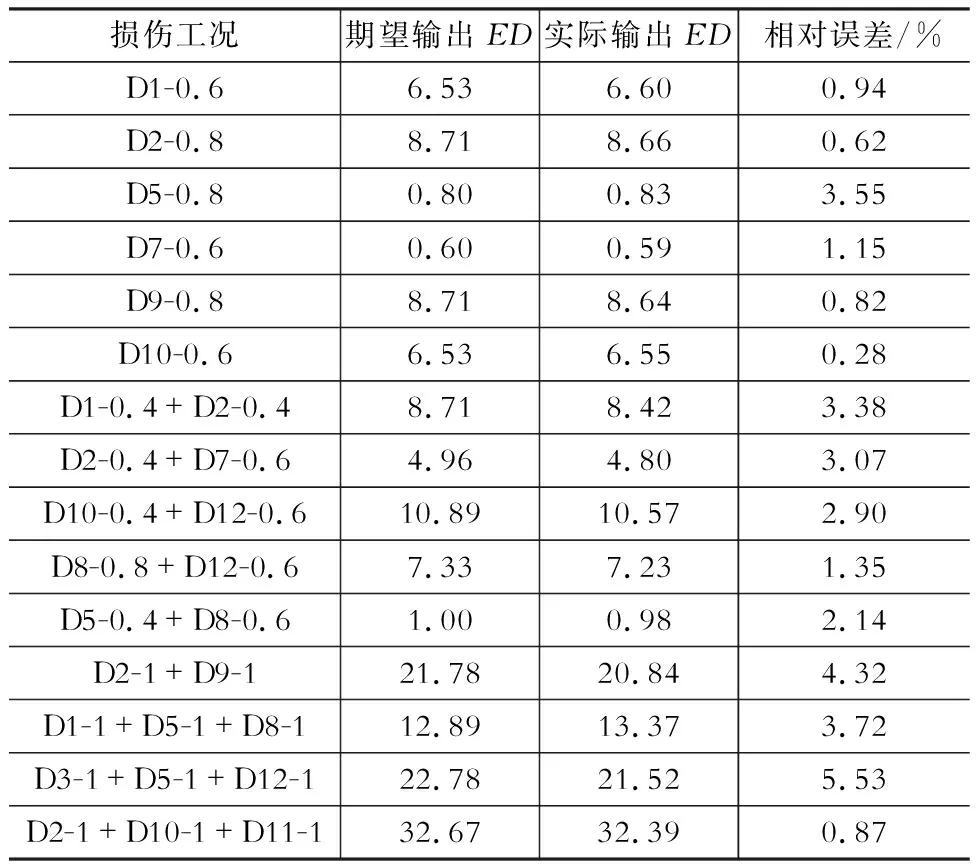
Table 3Results of elastic damage test

由兩表可以看出,對于彈性損傷,Enet的識別準確度較高,除工況D3-1+D5-1+D12-1外,其余工況的識別相對誤差均在5%以下,說明對于套筒連接的等效彈性損傷,BP神經網絡的識別是準確的;對于塑性損傷,Pnet的識別準確度不理想,一個重要的原因是訓練的輸入參數是由彈性響應得來的,彈性損傷系數ED直接和彈性響應相關,而塑性損傷系數PD與彈性響應不直接相關,導致其識別精度不如ED。

表4塑性損傷測試結果

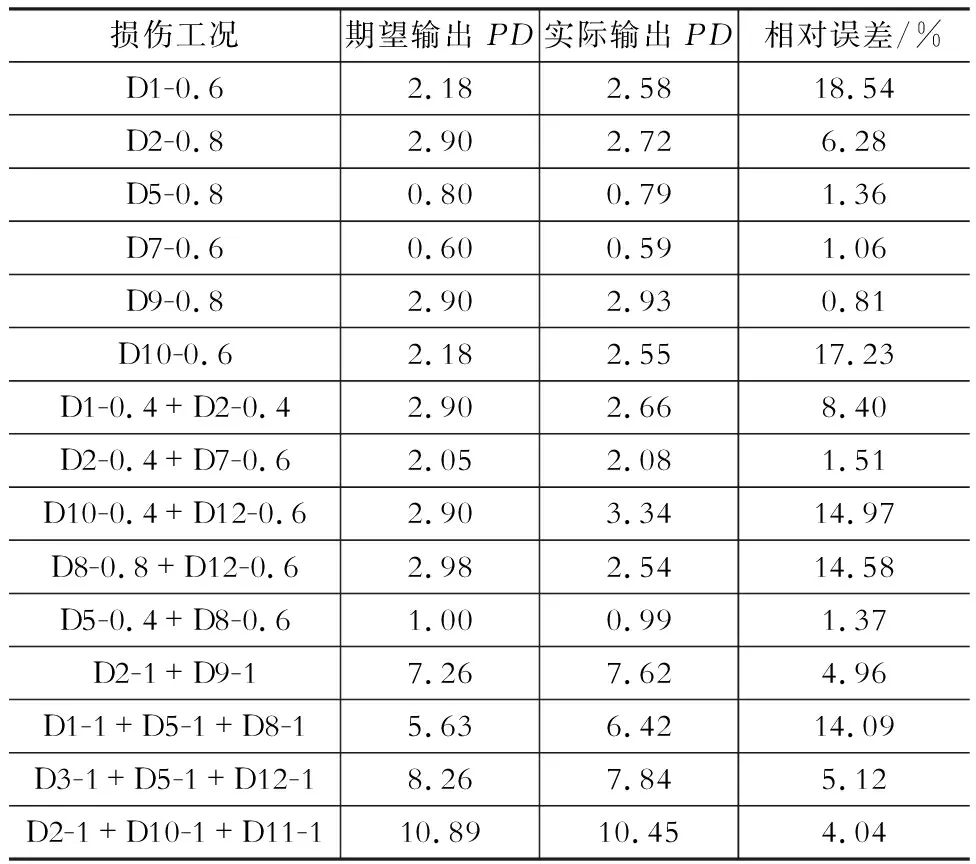
Table 4Results of plastic damage test

大多數情況下,ED值大于PD值,故若ED值小于塑性損傷的最大允許值,那么實際的PD值也是滿足要求的。

4 結 論

本文通過通用有限元軟件ABAQUS建模,模擬實際檢測中的瞬態沖擊,提取結構響應數據,利用Sym8小波分析提取裝配柱的彈性響應曲線的各個頻帶成分的能量占比,并選取能量占比變化量最大的三個頻帶的能量占比變化值構成能量特征值。將四個測點的能量特征值取平均,構造維數為3的特征向量作為BP神經網絡的輸入向量,定義了彈性損傷系數與塑性損傷系數,用以分別作為神經網絡的輸出值。通過數值模擬的方法獲得多種損傷工況下的訓練樣本用以訓練網絡,并獲得一系列測試樣本用以檢測網絡的識別能力。結果表明,訓練得到的神經網絡可以進行裝配柱套筒連接缺陷程度的識別,為實際工程中的檢測給出了參考。