配筋超強韌性混凝土偏心受拉構件力學分析
于明鑫,楊 楠
(沈陽城市建設學院新型建筑材料與結構科研團隊 沈陽市 110167)
工程水泥基復合材料(Engineered Cementitious Composite,簡稱為ECC)是一種具有高韌性的纖維混凝土,研究人員采用聚丙烯纖維(PP),研制出超強韌性混凝土(PP ECC),具有較高的材料抗沖擊能力和韌性[1],在單向受拉作用下應變硬化可以達到幾個百分比[2],韌性要比普通混凝土或一般纖維混凝土要高出很多,同時相比其他工程水泥基復合材料,如PVA ECC成本上又降低了很多[3]。基于以上原因,將超強韌性混凝土運用到承受偏心受拉荷載構件的實際工程中,例如公路、橋梁、機場建設等方面,具有十分優越的前景。
1 配筋超強韌性混凝土偏心受拉構件力學分析的基本假設
1.1 超強韌性混凝土拉伸應力-應變曲線

圖1 超強韌性混凝土抗拉應力-應變曲線

圖2 超強韌性混凝土抗壓應力-應變曲線
對配筋超強韌性混凝土偏心受拉構件進行分析,為方便理論計算,研究將配筋超強韌性混凝土構件中的超強韌性混凝土材料假設成在單軸受拉狀態下,其抗拉壓應力-應變曲線采用單線性模型。圖1、圖2為超強韌性混凝土抗拉應力-應變曲線和抗壓應力-應變曲線,簡化后本構模型如圖3、圖4所示。

圖3 超強韌性混凝土抗拉應力-應變曲線模型
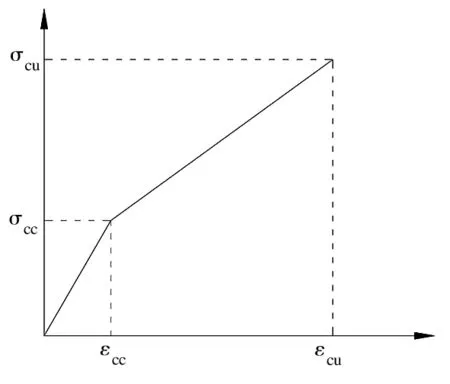
圖4 超強韌性混凝土抗壓應力-應變曲線模型
圖3所示超強韌性混凝土材料抗拉應力-應變[4]關系如下:
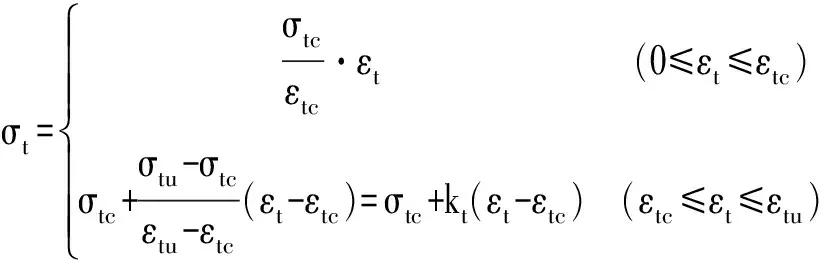
(1)
圖4所示超強韌性混凝土材料抗壓應力-應變[4]關系如下:
(2)
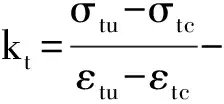
εtc-超強韌性混凝土受拉開裂應變;
σtc-超強韌性混凝土受拉開裂應力;
εtu-超強韌性混凝土受拉極限應變;
σtu-超強韌性混凝土受拉極限應力;
εcc-超強韌性混凝土受壓開裂應變;
σcc-超強韌性混凝土受壓開裂應力;
εcu-超強韌性混凝土受壓極限應變;
σcu-超強韌性混凝土受壓極限應力。
采用的參數,具體如表1[4]所示。

表1 超強韌性混凝土材料試驗性能設計值
1.2 鋼筋應力-應變曲線
分析計算中,鋼筋采用彈性-塑性雙直線模型[5],如圖5所示。

圖5 鋼筋彈性-塑性雙直線模型
該模型的數值方程如下:
(3)
其中,εy-鋼筋的屈服應變;
εu-鋼筋的極限應變,一般取0.01;
fy-鋼筋的屈服強度。
1.3 配筋超強韌性混凝土偏心受拉構件基本方程
超強韌性混凝土偏心受拉構件的受力模型如圖6所示。

圖6 偏心受拉構件基本模型
(1)配筋超強韌性混凝土構件的平衡方程如下[6]:
(4)
(5)
(2)配筋超強韌性混凝土構件變形協調方程如下[6]:
εs=εt=ε (εt≤εtu)
(6)
2 配筋超強韌性混凝土小偏心受拉構件力學分析
當配筋超強韌性混凝土構件小偏心受拉時,隨著偏心距的變化,配筋超強韌性混凝土構件所受軸力N與彎矩M所占的比重也在逐漸變化,構件截面會出現全截面受拉狀態,即εtc≤εb<εu,和部分截面受壓狀態,即0≤εb<εcc,兩種狀態。
2.1 全截面受拉狀態(εtc≤εb<εu)
該階段配筋超強韌性混凝土構件全截面受拉,近拉力側的鋼筋應變達到屈服點,遠拉力側的超強韌性混凝土處于拉伸應變硬化狀態,其應變為εb,如圖7所示。

圖7 配筋超強韌性混凝土構件全截面受拉狀態
圖7中鋼筋和超強韌性混凝土的應變關系,由幾何條件可得:
(7)
(8)
其中,εa-近拉力側超強韌性混凝土的應變;
εb-遠拉力側超強韌性混凝土的應變;
εs2-遠拉力側鋼筋的應變。
將式(7)和式(8)代入式(1)、式(3),將結果代入式(4),則可得:
(9)
σb=σtc+kt(εb-εtc)
(10)
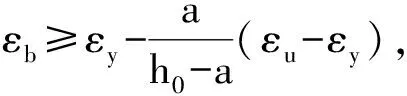
(11)
配筋超強韌性混凝土構件下端邊緣處對應的超強韌性混凝土應變為:
(12)
彎矩由近拉力側超強韌性混凝土和遠拉力側超強韌性混凝土的應力差產生,將鋼筋和超強韌性混凝土的應力代入式(5)中,得到彎矩的表達式:
(13)
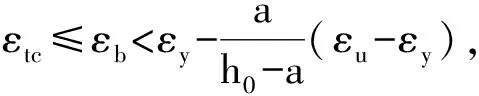
(14)
當N已知時,配筋超強韌性混凝土構件下端邊緣處對應的超強韌性混凝土的應變為:
(15)
將鋼筋和超強韌性混凝土的應力代入式(5)中,得到彎矩M的表達式:
(16)

當εb<εtc時,將其代入式(14)、(16)得:
(17)
(18)
2.2 部分截面受壓狀態(0≤εb<εcc)
該階段受拉區鋼筋應變達到塑性極限,受壓區超強韌性混凝土處于受壓彈性階段,其應變為εb,如圖8所示。

圖8 配筋超強韌性混凝土構件部分截面受壓狀態
圖8中所示鋼筋和超強韌性混凝土的應變關系,由幾何條件可得:
(19)
(20)
(21)
(22)
(23)
將式(21)和式(20)代入式(1)、式(3),即可到超強韌性混凝土的應力和鋼筋的應力,將結果代入式(4),則軸力N為:
(24)
將鋼筋和超強韌性混凝土的應力代入式(5)中,可得到彎矩M的表達式:
(25)
3 配筋超強韌性混凝土大偏心受拉構件力學分析
大偏心受拉構件截面同時存在受拉區和受壓區。由于實際工程中的配筋超強韌性混凝土受拉構件基本都采用對稱配筋,在大偏心拉力作用下,受壓區的超強韌性混凝土還沒有達到極限壓應變,拉區的鋼筋就會屈服以致構件破壞。對其進行力學分析主要分成兩部分狀態,受壓側邊緣超強韌性混凝土的應變為εcc<εb<εcu和受壓側邊緣超強韌性混凝土的應變為εcc≥εb。
3.1 受壓側邊緣超強韌性混凝土的應變為εcc<εb<εcu
當受壓側邊緣超強韌性混凝土應變εcc<εb<εcu,如圖9所示。

圖9 配筋超強韌性混凝土構件受壓區邊緣超強韌性混凝土塑性狀態
構件受壓區應力圖按照雙直線變化,由配筋超強韌性混凝土構件應變圖的幾何關系可得:
(26)
(27)
(28)
(29)
(30)
根據平截面假定可得:
(31)
由式(1)和式(2)可得超強韌性混凝土的應力沿構件截面高分布為:
σ(x)=
(32)
(1)當εs2<εy時,鋼筋應力為:
(33)
由力和力矩的平衡可得軸力Nu和彎矩Mu為:
(34)
(35)
(2)當εs2>εy時,鋼筋的應力為:
σs1=fy
(36)
由力和力矩的平衡可得軸力Nu和彎矩Mu為:
(37)
(38)
3.2 受壓側邊緣超強韌性混凝土的應變為εcc≥εb
當受壓側邊緣超強韌性混凝土應變為εcc≥εb,如圖10所示,配筋超強韌性混凝土構件受壓區應力圖按照單直線變化。
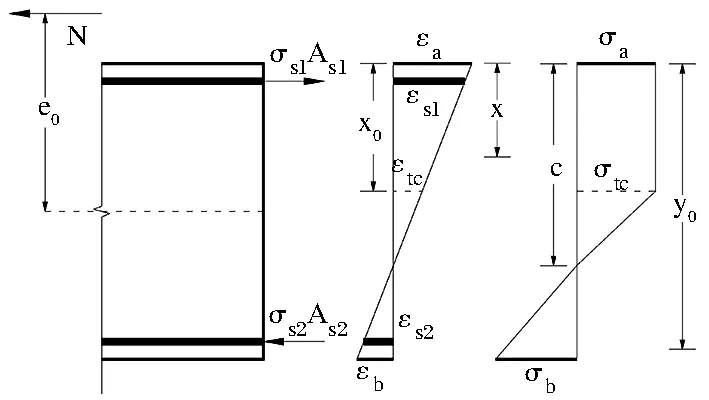
圖10 配筋超強韌性混凝土構件受壓區邊緣超強韌性混凝土彈性狀態
鋼筋的應力為:
(39)
由力和力矩的平衡可得軸力Nu和彎矩Mu為:
(40)
(41)
4 結論
通過對配筋超強韌性混凝土偏心受拉構件進行分析,得出以下結論:
(1)超強韌性混凝土構件在偏心受拉過程中始終承受拉力作用。
(2)小偏心受拉鋼筋超強韌性混凝土構件的力學分析分成三個階段,通過分析得到了各個階段的承載力公式。
(3)大偏心受拉鋼筋超強韌性混凝土構件,對受壓側應變的不同而分為兩個階段,通過分析得到了各個階段的承載力公式。

