基于粒子群算法的極限學習機短期電力負荷預測

（河北工業大學 經濟管理學院，天津 300401）

0 引言

隨著智能電網行業的市場化，短期負荷預測對當前電力行業資源優化和調度分配至關重要。短期負荷預測一般是指預報未來幾天乃至未來一個月的電力負荷預測，它不但為電力系統的經濟和安全運行提供保障，也影響著電力系統的大多數決策制定[1]。近年來，隨著人工智能研究的進展，現代智能算法代替了傳統的預測方法在短期電力負荷預測中得到了廣泛的應用，如神經網絡[2,3]、支持向量機[4,5]等。

傳統人工神經網絡已被廣泛應用于多層前饋神經網絡的訓練中，但是傳統人工神經網絡存在收斂速度慢、容易陷入局部極小值以及相關參數調整復雜等不足。極限學習機（Extreme Learning Machine，ELM）是Huang等人提出的一種特殊單隱層前饋神經網絡方法[6]。相比較于傳統前饋神經網絡，ELM網絡只需設置特定的隱含層節點數，且算法在運行過程中輸入層與隱含層之間的輸入權值和隱含層偏差被隨機初始化給定，輸出權值矩陣利用廣義逆（Moore-Penrose）計算得到，整個過程一次性得到最優解。ELM算法比傳統神經網絡算法運行速度更快、精度更高、參數調整簡單，受到了海內外學者的廣泛研究關注。但是，在算法運行過程中，ELM網絡的隱含層偏置和輸入權值被隨機給定，產生的隨機參數會給輸出權值造成一定的誤差。

針對ELM存在的問題，本文提出了一種混沌自適應粒子群優化算法（Chaotic Adaptive Strategy Particle Swarm Optimization, CSPSO）來優化極限學習機中的連接權值和閾值，計算輸出權值矩陣，達到減少隨機參數誤差的目的。針對粒子群算法初期存在空間中無法均勻分布、種群多樣性下降以及部分群體偏離最優解等問題。本文采用Logistic混沌映射代替PSO粒子更新方程中的隨機參數r1與r2，使種群粒子不重復地遍歷整個群空間，從而精確地定位最優解的空間位置。另外，針對種群尋優后期粒子容易陷入停滯的問題，引入一個自適應判斷策略。該策略以聚合度為影響因子動態生成判別概率，并判斷CSPSO算法產生的隨機數是否滿足進行混沌搜索的條件。最后利用粒子群全局搜索得到的最優輸入權值與隱含層偏差值計算ELM網絡輸出權值矩陣。通過與其他模型的比較，驗證了改進的粒子群極限學習機在網絡泛化性和精度上的優勢。

1 極限學習機

ELM的單隱含層前饋神經網絡結構如圖1所示，該神經網絡由輸入層、隱含層和輸出層組成。隱含層與輸出層神經元間全連接，其中隱層偏置B=（b1，b2，…，bi），輸入權值W=（w11，…，w1z，w21，…，w2z，…，wt1，…，wtz），輸出權值β=（β1，β1，…，βz），具體算法描述如下：

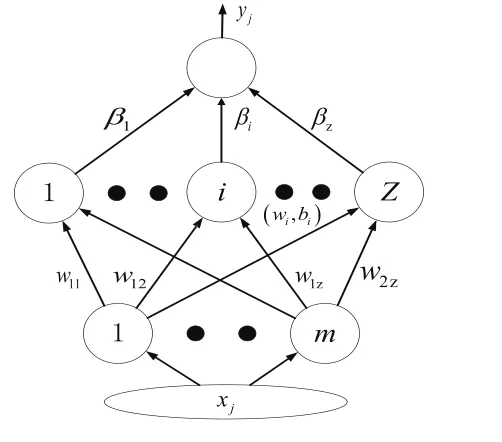
圖1 ELM 的網絡結構

給出一定數量的訓練樣本（xi，yi），根據給定的激勵函數f，由前饋神經層最終可得預測值yi如下：

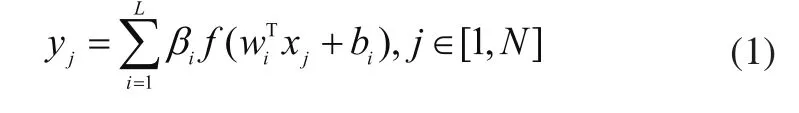
式(1)中，（wi，bi）參數被隨機選取，iβ是輸出權值，由下列步驟計算得到。

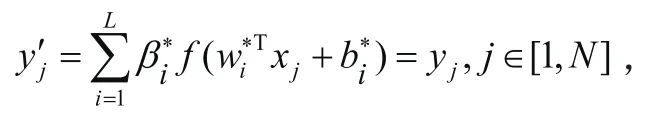
其中，式(3)的H為隱層輸出矩陣：

W、B的取值確定后，根據最小二乘法解得：

其中H+為H的廣義逆矩陣。

2 基于改進粒子群優化的極限學習機

2.1 混沌粒子群

混沌粒子群算法是一種群體智能的優化算法更是一種良好的全局搜索最優解算法，它比標準粒子群有著更好的多樣性和全局收斂性[8]。設種群規模為n，搜索維數為m，第i個粒子位置可以表示為xi=（xil，xi2，…，xiD），速度為vi=（vil，vi2，…，viD），粒子個體所經歷最優位置pbesti=（pbesti1，pbesti2，…，pbestiD）種群粒子經歷最優位置gbest=（gbest1，gbest2，…，gbestD）。粒子的更新速度和粒子的當前位置如式(1)、式(2)所示：

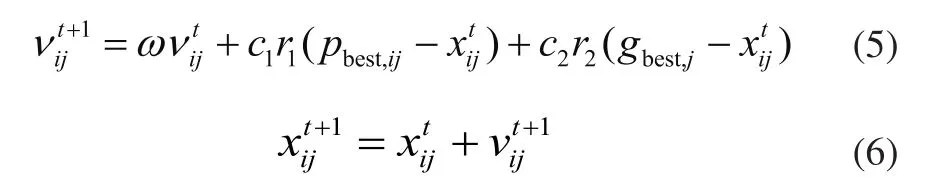
r1和r2兩個參數都是[0，1]上Logistic混沌映射的隨機數，w為慣性權重系數。將相對誤差（Mean Square Error，MSE）作為評價粒子群優劣的適應度值，其定義為式(3)：

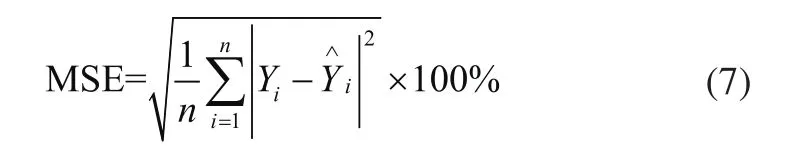
Logistic映射式如下：

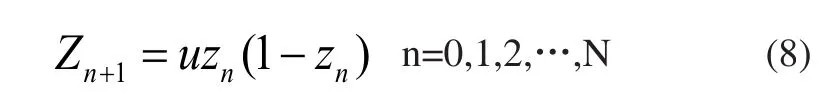
其中，u是控制參數的值u∈（0，4]；Zn是第n個混沌變量Zn∈[0，1]。u=4時，此時解空間處于混沌狀態，混沌空間是[0，1]。

2013年，天津市水務局作為天津市河道水生態環境管理領導小組辦公室牽頭單位，積極推進河長制管理制度的建立與落實，在全市范圍內初步建立起較為完整的水生態環境管理組織體系。

在混沌搜索初始時對式(8)賦予原始隨機數，產生一個m維并且每一維分量在0～1的向量z1=（z11，z12，…，z1m），同時用式(8)得到N個z1，z2，…，zN，將zn的所有分量映射到優化變量的取值xij=xmin+Zij（xmaxxmin）（i=0，1，2，…；j=1，2，…，Q）并計算適應度函數值f（xij），如果f（xij）＞f（xmax），則xmax=xij，如果達到迭代停止的條件，則立即停止迭代過程。否則種群開始重新進行混沌搜索。

2.2 自適應策略

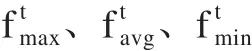
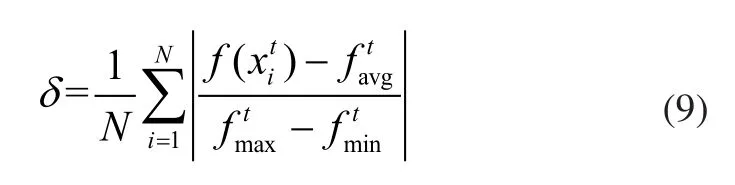
根據聚合度δ動態地調整CSPSO算法粒子的判斷概率，設第t代的判斷概率為其公式如下所示：

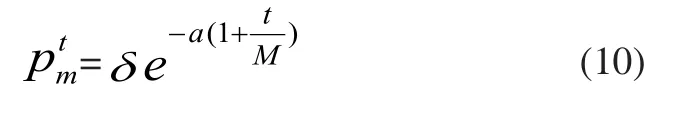
上式中a是設置的參數用來調控判斷概率變化速度，取值大小為[2，4]。

本文用改進的粒子群算法優化極限學習機中的連接權值和閾值，建立短期電力負荷預測的CSPSO-ELM模型，將極限學習機的輸入權值和閾值作為粒子群算法的粒子。粒子長度為D=Z×（m+1），其中Z為隱含層節點數目，m為輸入向量維數，θk為種群中的第k(1≤k≤popsize)個粒子：

θk=其中為[-Xmax，Xmax]中的隨機數，一般Xmax=1。具體操作為：

輸入 訓練集矩陣（xi，yi），

3 實驗及結果分析

3.1 數據處理評價指標

實驗數據采自阿里巴巴和大航集團聯合舉辦的大航杯天池電力AI大賽的電力預測大賽。利用歷史數據2015年3月～10月和2016年3月～8月內1416家當地企業的日用電總負荷值、歷史天氣情況、歷史氣溫、歷史相對濕度以及節假日和當地月工業產值等數據，預測2016年9月份的揚州市高新區每天總用電量數據。揚州市高新區當地最高溫度、最低溫度、天氣、濕度、節假和工業產值部分特征處理情況如表1所示，九種天氣情況量化處理如表2所示。

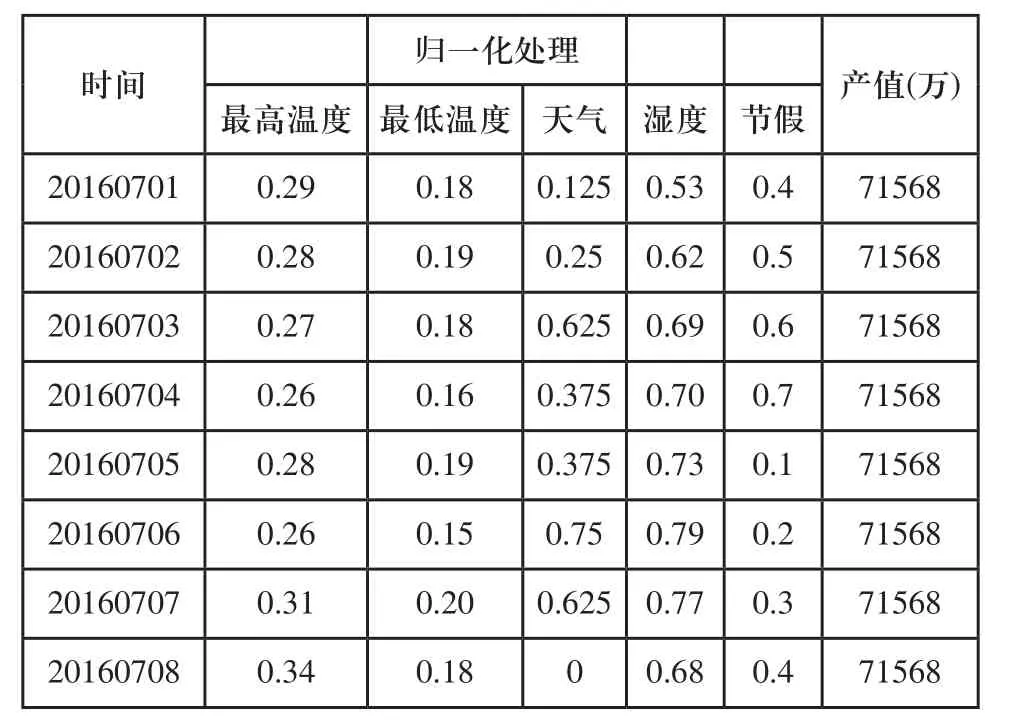
表1 揚州市高新區當地特征因素

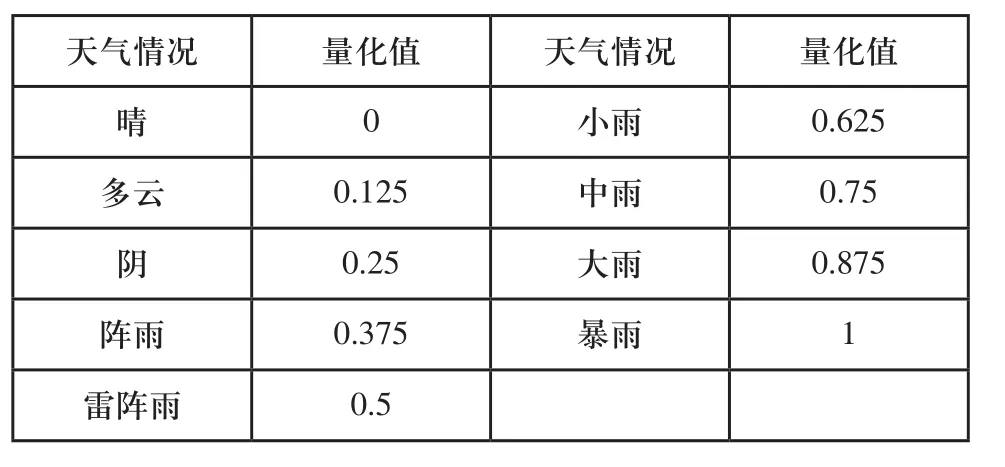
表2 天氣情況量化處理

3.2 評價指標

為了評估本文算法，實驗分別采用均方根差（RMSE）、平均相對誤差（MAPE）、平均絕對值誤差（MAE）和擬合優度R平方公式作為算法的評價標準：

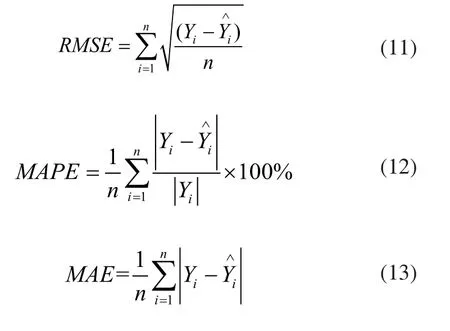
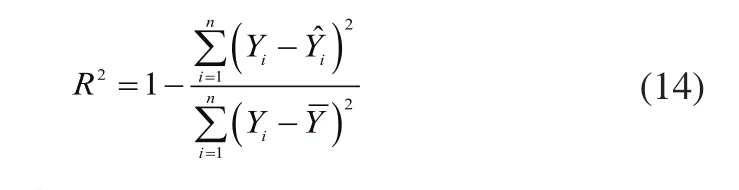
3.3 預測精度分析

根據以往文獻[9]和文獻[10]的參數研究，將極限學習機的隱藏節點數設置為20，隱層激活函數為Sigmoid。設置 PSO和CSPSO的加速度因子C1，C2=2，種群規模為n=30，最大進化代數Gmax=100，不敏感函數ε= 0.01，參數C及參數 搜索范圍和搜索速度分別是[0.02,10]和[-3,3]，設置慣性權重wmin=0.2，wmax=0.8。

將處理好的最高溫度、最低溫度、天氣、濕度、節假、預測日前八天用電數據和工業產值特征因素輸入矩陣中，分別用訓練好的PSO-ELM、ELM和CSPSO-ELM預測模型對數據進行負荷預測。預測得到九月份30天的用電數據如圖2所示，基于ELM算法建立的極限學習機模型與實際負荷曲線相差較大，預測準確度不高；基于PSO-ELM算法建立的極限學習機模型預測擬合度較好，預測準確度較為準確；基于CSPSO-ELM算法建立的預測模型擬合程度和精確程度優于上述兩種模型。三種模型評價標準值如表3所示，由預測結果和評價指標值對比發現，CSPSO極限學習機機模型的 和 都明顯低于其它兩種模型的RMSE和MAE值。同時CSPSO極限學習機模型尋優效率高于PSO極限學習機模型。這充分說明了CSPSO比PSO和ELM算法選取參數的效果更好。

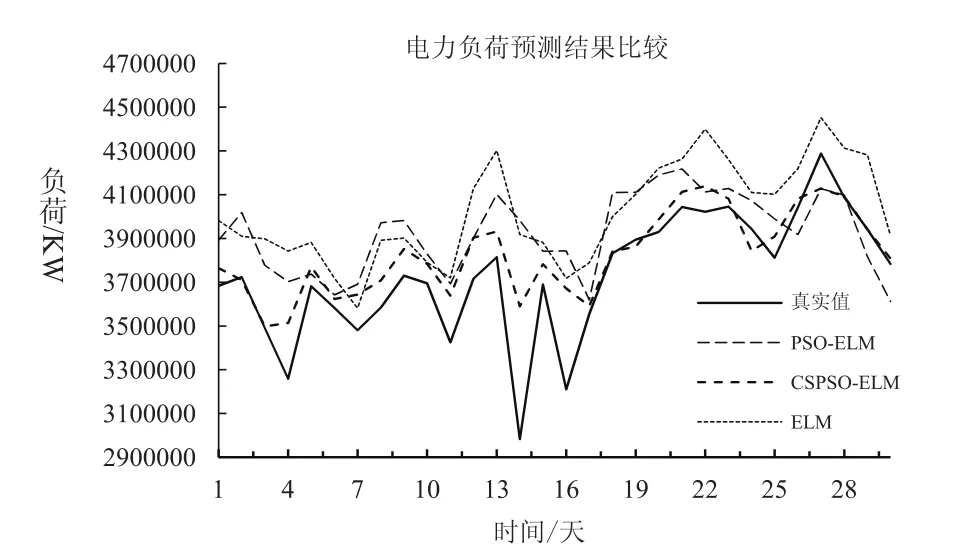
圖2 電力負荷預測結果比較

表3 ELM模型基于不同參數尋優算法的結果對比

4 結論

本文將混沌算法和自適應策略與PSO-ELM算法相結合，通過混沌算法提升種群粒子的多樣性，增強粒子隨機初始分布的效率。同時利用自適應策略及時判斷算法是否進行混沌搜索，防止種群過早陷入收斂。在充分考慮了氣象因素、溫度因素、濕度因素、節假日因素和當地工業產值因素對用電量預測的影響下，建立CSPSO極限學習機的預測模型。仿真結果表明，CSPSO算法能夠精準的搜索極限學習機網絡的權值和偏置，得到最佳輸出權重范數，從而使得ELM短期預測模型具有更高的預測精度。