渦流檢測磁化管道時頻率對線圈阻抗的影響

，， ，

(1.中油管道檢測技術有限責任公司，廊坊 065000；2.大慶油田有限責任公司 天然氣分公司，大慶 163000)

隨著油氣供需量的不斷增大，油氣管道的口徑和運行壓力也隨之增大。管道在運營初期和長期服役以后，管材、施工質量、外部干擾、土壤等周圍環境以及高壓、高速的輸送介質都會對管道造成腐蝕、裂紋、變形等損害，如不及早發現并預防，很有可能導致管道失效而造成重大安全事故。因此，必須定期對管道進行檢測和安全評估。管道內檢測技術被廣泛應用于油氣管道的無損檢測作業中[1-2]。由于漏磁、渦流技術不受輸送介質的限制，且具有檢測效率高等優點，是目前應用最為成熟的管道內檢測技術。霍爾傳感器和渦流線圈可集成在同一個探頭殼體內，將二者采集到的數據進行綜合分析可以提高對缺陷的檢測能力。渦流線圈的阻抗變化除了與缺陷自身有關外，還與激勵信號的頻率密切相關。因此，研究渦流線圈經過內外壁缺陷時，不同的激勵頻率對線圈阻抗的影響規律，對渦流檢測電路的設計和信號特征的判別具有重要意義[3-6]。

目前國內直徑為1 000 mm及以上的油氣管道材料多為X80鋼，當檢測探頭寬度不大于40 mm時，該類油氣管道與管道內壁貼合。由于曲率造成的最大提離值小于0.2 mm，這個值相對于缺陷深度可忽略不計，由此可用平板代替大口徑鋼管作為研究對象。利用ANSYS Maxwell 有限元仿真軟件，以X80鋼板做為被測體，仿真計算了不同激勵頻率的渦流線圈經過鋼板內外表面上缺陷時線圈阻抗的變化規律，并按仿真模型同比例制作了測試平臺，在測試平臺上用阻抗分析儀測量了檢測線圈的阻抗，測量結果與仿真結果吻合。

1 模型建立

1.1 ANSYS Maxwell二維渦流場仿真的理論基礎

通過式(1)，(2)組成的方程組來計算A和φ，并完成對渦流問題的求解。

(1)

式中：A為矢量磁位；φ為標量電位；σ為電導率；ε為介電常數；ω為時諧場的角頻率；μ為磁導率。

(2)

式中：Ω為導體橫截面積域；IT為導體的總電流。

這兩個公式都可以通過時諧麥克斯韋方程組推導得出，其表達式如式(3)所示。

(3)

式中：B為磁感應強度；E為電場強度。

將矢量磁位A的定義式×A=B和電場E與A的關系式E=-jωA-φ，代入到式(3)可得到式(1)，其右側是復數電導率σ*=σ+jωε與電場強度E=-jωA-φ的乘積，其結果是復數電流密度J。其包含有3個分量：Js=-σφ為源電流密度，與標量電位的微分相關；Je=-jωσA為感應渦流密度，由時變的磁場產生；Jd=jωε(-jωA-φ)為位移電流密度，由時變的電場產生。

求解問題時，通常需要確定的是與激勵源相連的導體內的總電流，因此，將式(1)右側部分在導體橫截面域內進行積分就可求得流過導體的總電流。

1.2 實體模型參數

為了仿真不同激勵頻率的線圈經過內外壁缺陷時的阻抗，建立ANSYS Maxwell二維渦流場(見圖1)。鋼板的厚度為W，長度為2L，電導率為σ1，在鋼板內外側分別加工缺陷，缺陷長度為2L1，深度為W1。渦流線圈采用扁平柱狀空心放置式線圈，并將其置于被測鋼板上方1 mm處，其內徑為R1，外徑為R2，高度為W2，電導率為σ2。

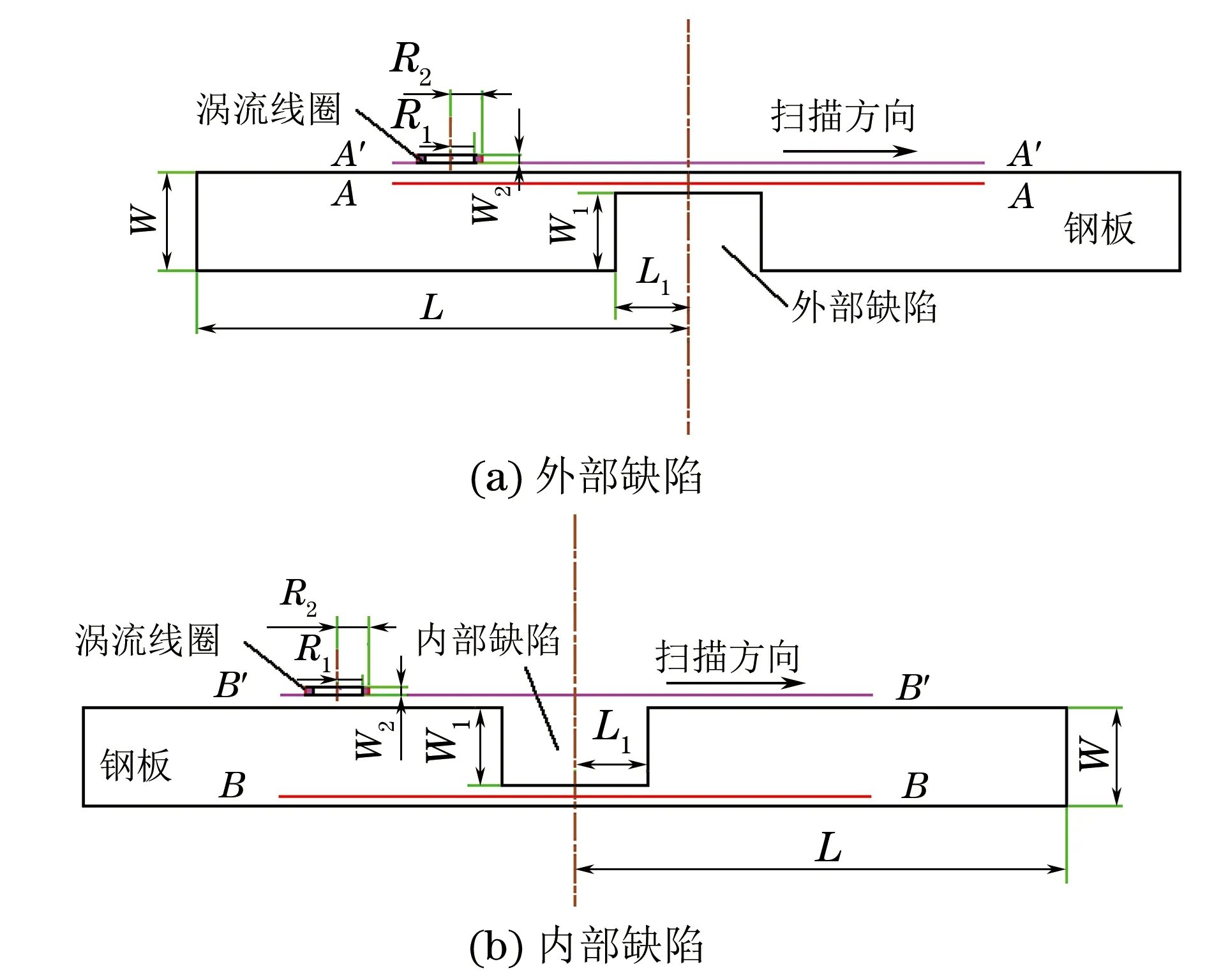
圖1 外部缺陷和內部缺陷的二維渦流有限元模型

仿真模型采用二維笛卡爾坐標系xy平面模型，整個分析域應當向x，y方向無限延伸，但實際數值計算中，求解域用一個足夠大的有限背景空氣區域代替，因此，有限區域邊界上的場量不能強制為0。研究中將背景區域周圍4個邊界都設成氣球邊界，磁場既不平行也不垂直于氣球邊界。由于線圈與背景區域交界條件為自然邊界條件，這意味著跨越物體之間界面磁場強度H的切向分量和磁感應強度B的法向分量是連續的，其由泛函求極值自動滿足，因此不用考慮[3]。同時仿真模型需要滿足以下假設條件：① 時變電磁場做周期性變化，其表達式為F(t)=Fmcos(ωt+θ)；② 所有量必須有相同的角頻率，但可以具有不同的相角；③ 所有電流量與導體的橫截面正交；④ 忽略渦流探頭的運動速度；⑤ 線圈中的渦流忽略不計；⑥ 模型中各種材料的電導率在計算范圍內設為常量。

仿真時渦流線圈沿缺陷一側經缺陷中心以步長d移動到另一側，形成測量路徑A′-A′和B′-B′，線圈每個步長移動后的位置為xi。

1.3 確定仿真參數

鐵磁性材料被飽和磁化后，位于內外壁缺陷處的磁導率將發生明顯變化。因此，鋼板的磁導率不能用B-H表征，采取如下的方法計算鋼板的相對磁導率μr。

(1) 將檢測線圈內徑圓周的外切正方形CC′DD′劃分成nxn個小單元。檢測線圈面積劃分示意如圖2所示。

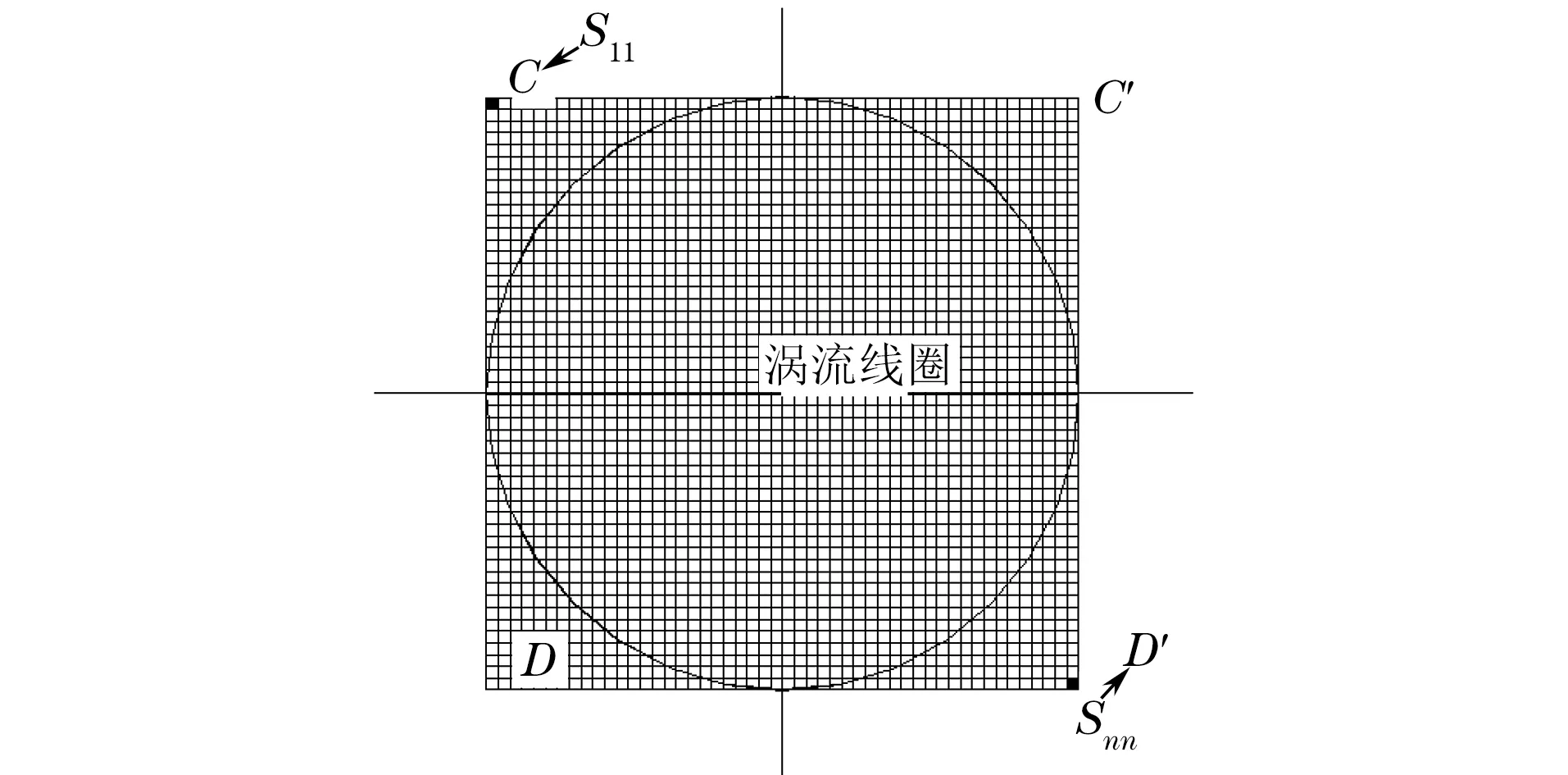
圖2 檢測線圈面積劃分示意

將落在線圈內的單元做歸一化處理，計算出各小單元所占線圈總面積的比例，線圈外部的小單元面積設為0，從而構造nxn維矩陣C。

(4)

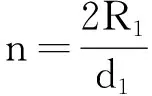
(5)

式中：R1為線圈內圈半徑；d1為掃描步長。

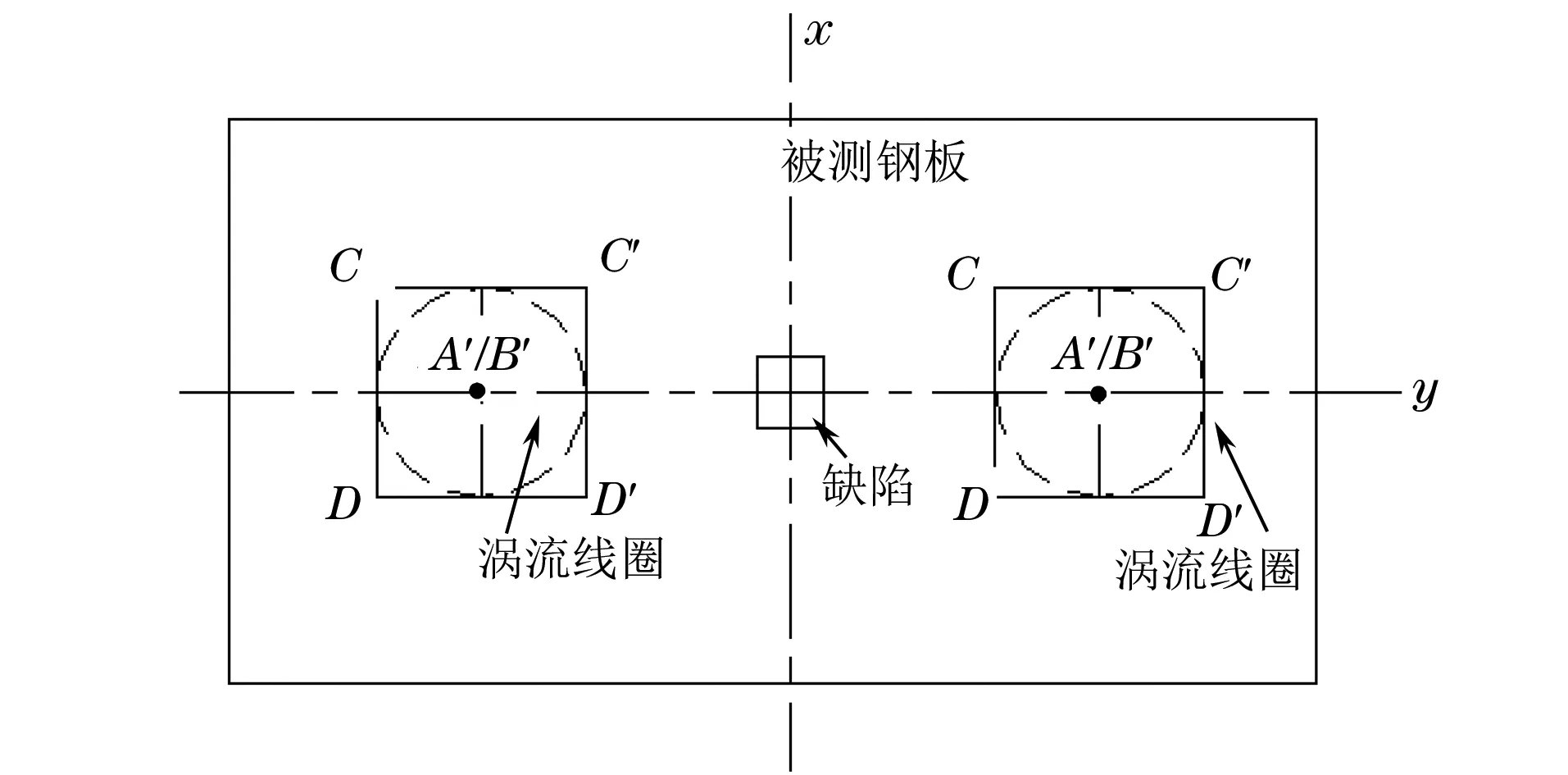
圖3 測量路徑示意

(2) 將包含渦流線圈的正方形CC′DD′置于缺陷側鋼板上方1 mm處，沿缺陷一側經缺陷中心以步長d移動到另一側，形成測量路徑A′-A′和B′-B′,這樣形成m個測量點，測量路徑示意如圖3所示。

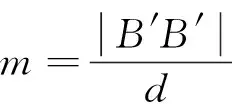
(6)

(3) 將每個測量點處正方形CC′DD′下方鋼板上仿真得到的相對磁導率，在x，y方向均以步長d計算生成m個n維方陣MiUr。

(4) 用n維方陣C點乘n維方陣MiUr后得到m個C*MiUr方陣，對每個方陣中的所有元素求和，得到的值就是每個計算位置線圈下的等效平均相對磁導率μri。

渦流線圈的阻抗為

Z=R+j2πfL

(5)

式中：Z為線圈的阻抗；R為線圈的電阻；L為線圈的電感；f為激勵頻率。

阻抗角θ可由式(6)求得。

(6)

仿真時將線圈的掃描位置x和激勵頻率f作為參數變量，仿真過程中通過賦給線圈每個位置xi對應鋼板的線圈面積覆蓋區的平均相對磁導率μri，可以直接計算出不同頻率時每個掃描位置xi處線圈的電阻R和電感L，結合對應的激勵頻率還可以算出線圈等效阻抗Z及阻抗角θ。

2 仿真及試驗結果

模型中鋼板的厚度為10 mm，長度為200 mm，電導率為0.46×107S·m-1，缺陷長度為40 mm，深度為7 mm。渦流線圈內徑為5 mm，外徑為6 mm，高度為1 mm，電導率為0.58×108S·m-1，線圈匝數為40，激勵源選用電流源，電流為0.5 A，激勵頻率f分別選擇20，200，2 000 kHz。掃描長度為100 mm。

線圈的電感、電阻、阻抗及阻抗角與掃描位置的關系如圖4～7所示。

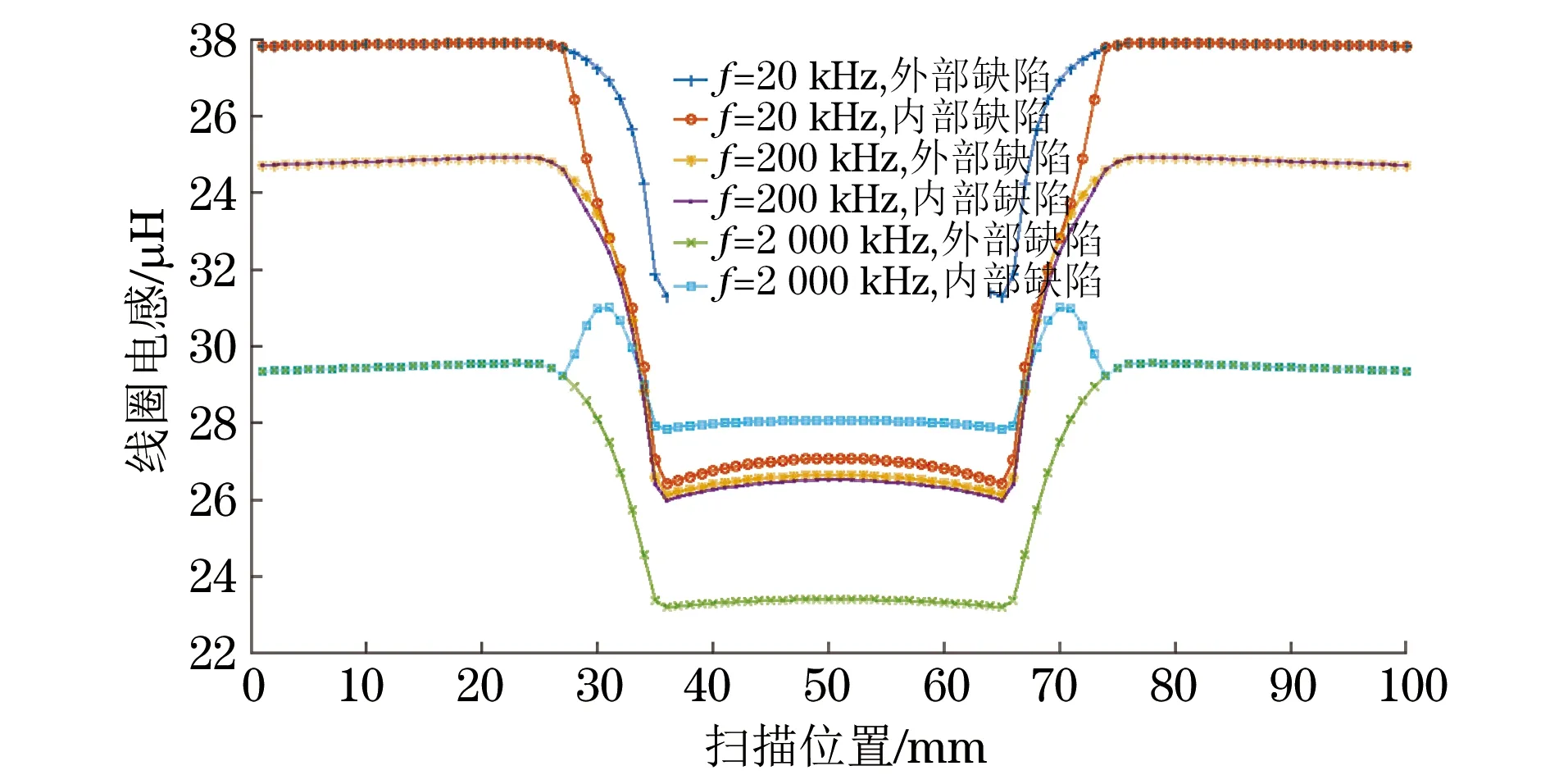
圖4 線圈電感與掃描位置關系

不同頻率時，仿真線圈中的電感、電阻、阻抗和阻抗角在內外部缺陷的邊沿處、中心處的變化規律及與基值(無缺陷時的值)的比較結果如表1所示(表中符號△表示數值增大，表示數值減小，=表示數值基本不變，< 表示數值小于基值，> 表示數值大于基值，— 表示與基值相當)。

為了驗證仿真結果，設計的測量系統組成如圖8所示。測量系統由勵磁電源、電磁鐵、帶缺陷的測試鋼板、渦流線圈和阻抗分析儀等組成，系統中各部件的尺寸及材料如表2所示。

表1 不同頻率時被測物理量的統計結果

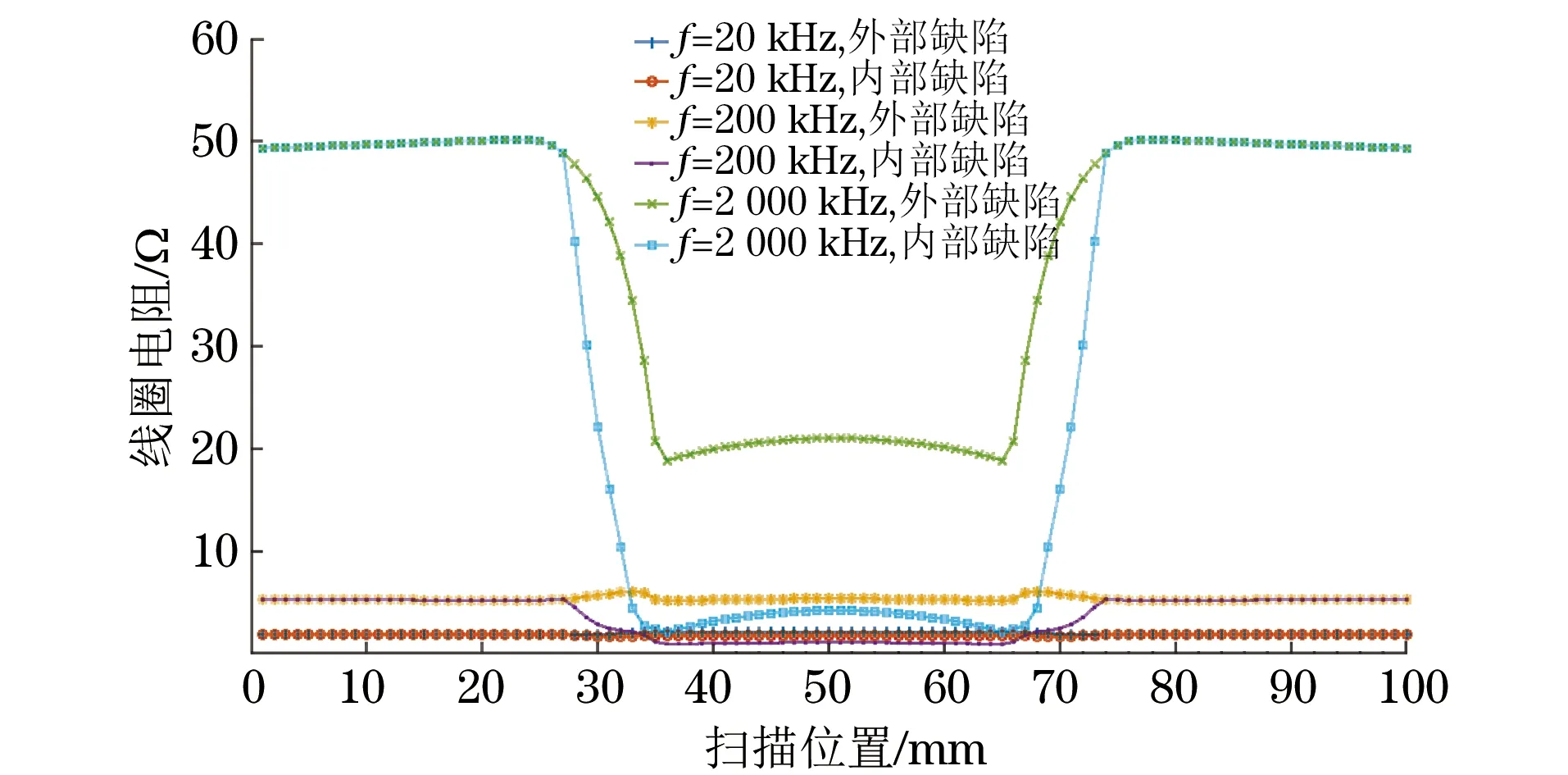
圖5 線圈電阻與掃描位置關系

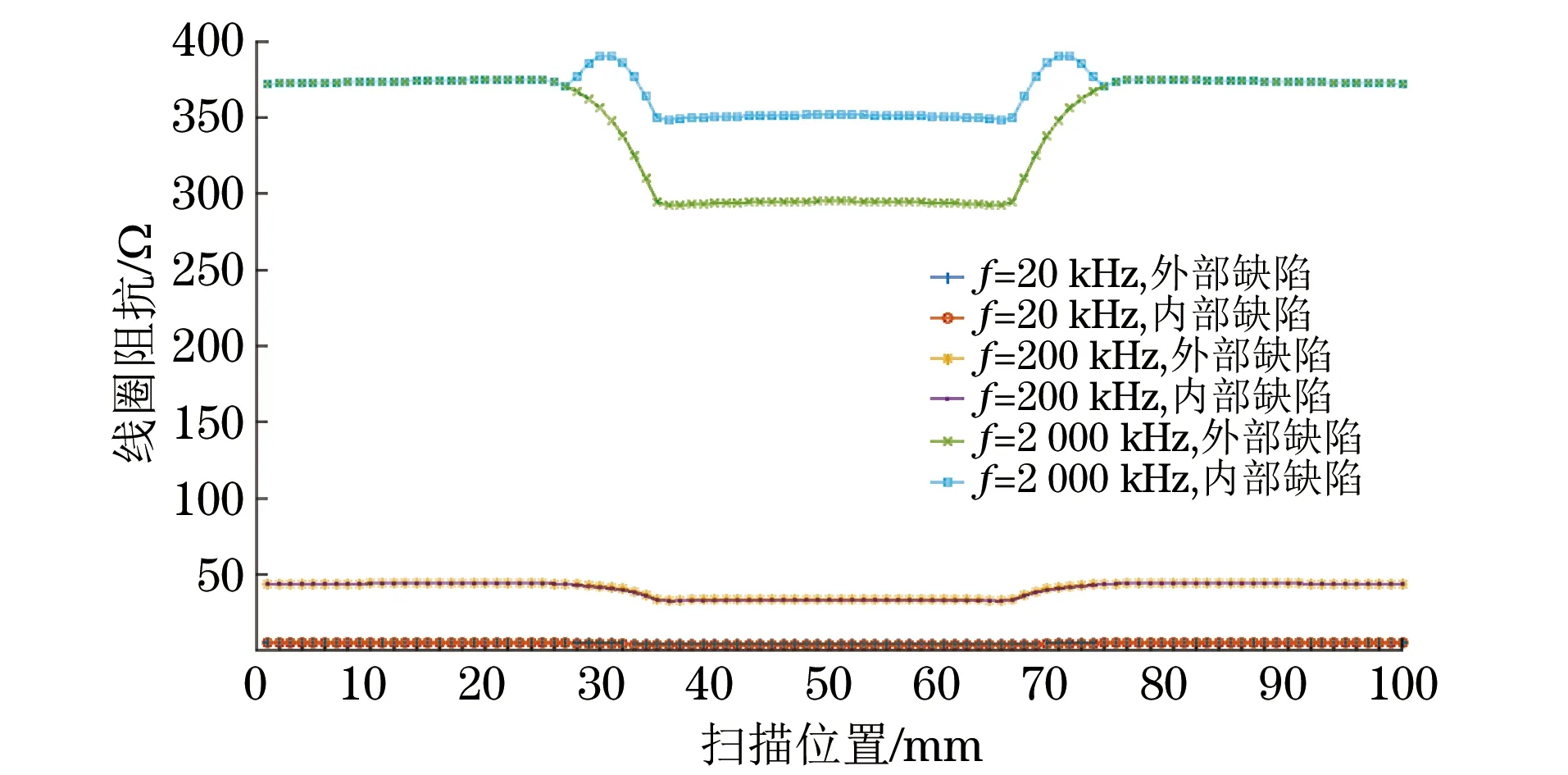
圖6 線圈阻抗與掃描位置關系

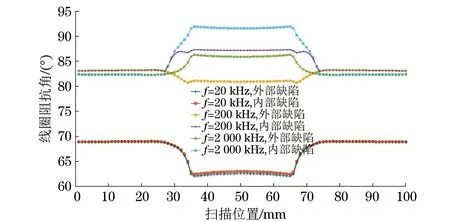
圖7 線圈阻抗角與掃描位置關系

圖8 設計的測量系統組成

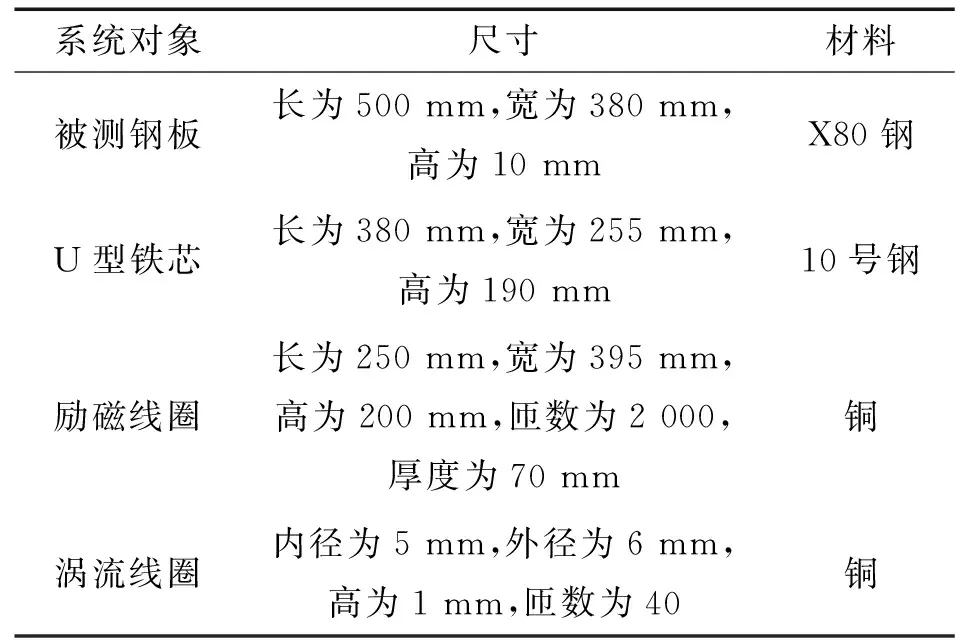
系統對象尺寸材料被測鋼板長為500 mm,寬為380 mm,高為10 mmX80鋼U型鐵芯長為380 mm,寬為255 mm,高為190 mm10號鋼勵磁線圈長為250 mm,寬為395 mm,高為200 mm,匝數為2 000,厚度為70 mm銅渦流線圈內徑為5 mm,外徑為6 mm,高為1 mm,匝數為40銅

按照圖1所示在被測鋼板上加工尺寸為40 mm×40 mm×7 mm(長×寬×深)的人工缺陷，對勵磁線圈施加6.5 A的直流電，經測量和計算，此時鋼板的磁化水平約為20 kA·m-1。渦流線圈以步進長度為0.2 mm沿如圖1所示A′-A′和B′-B′路徑掃描，設備為Agilent公司的型號為4294 A的阻抗分析儀，其測量顯示畫面如圖9所示。當激勵頻率分別為20，200，2 000 kHz時，測量線圈的電感、電阻、阻抗和阻抗角。線圈電阻和阻抗角的實測結果如圖10，11所示。

圖9 阻抗分析儀測量顯示畫面

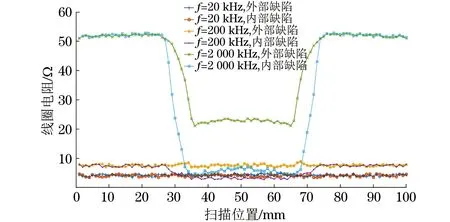
圖10 線圈電阻實測結果

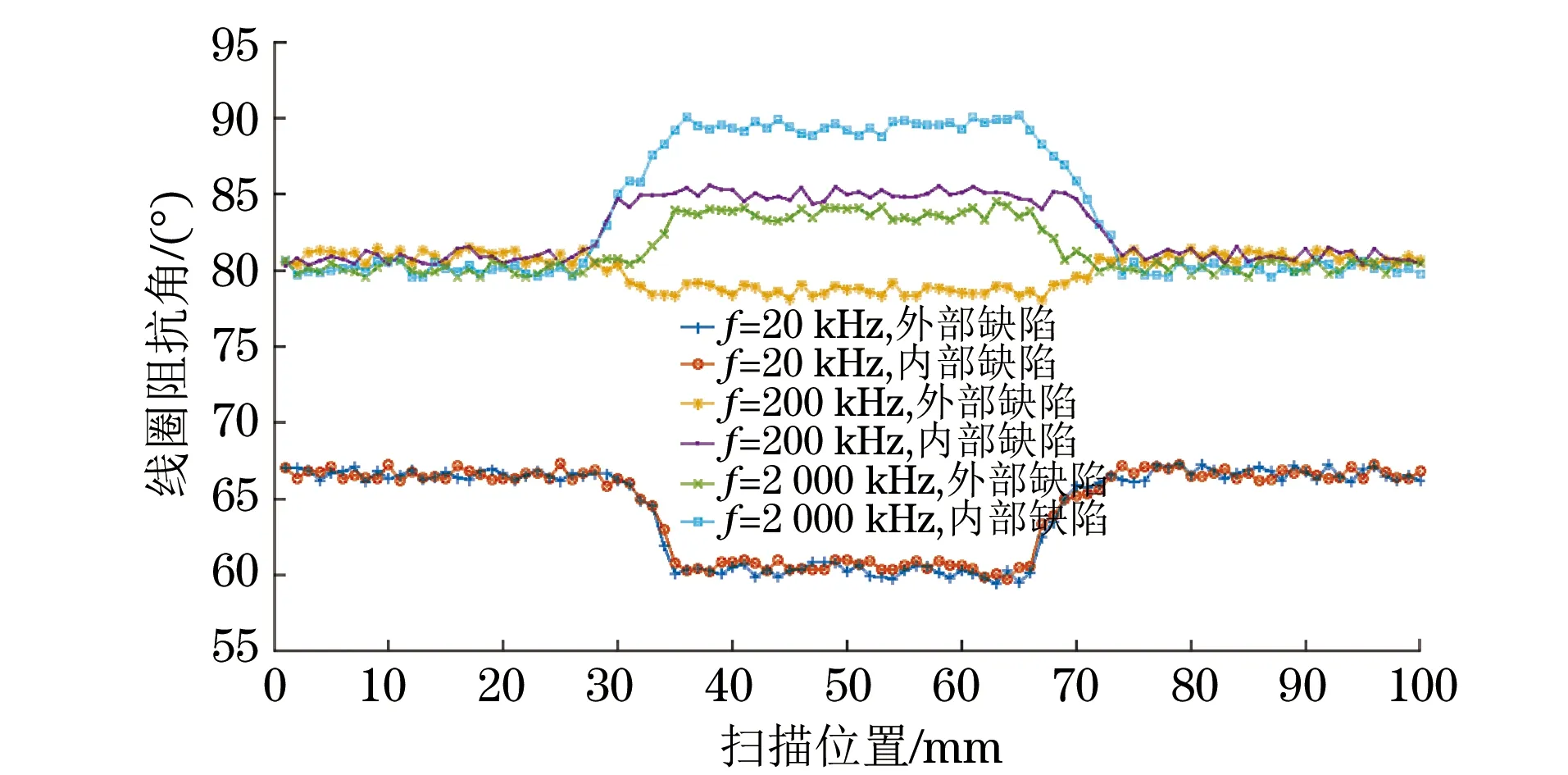
圖11 線圈阻抗角實測結果

3 結論

(1) 在頻率為20 kHz時，線圈掃描經過內外部缺陷時的L和θ都隨缺陷的出現迅速減小，并在缺陷處減小到最小值，Z的變化量也很小。

(2) 在頻率為200 kHz時，線圈掃描經過內外部缺陷時的L和Z的變化規律與頻率為20 kHz時L和θ的變化規律基本相同；在線圈掃描經過內部缺陷時，R隨缺陷出現而減小，在缺陷中心處的R小于無缺陷時的值，而線圈掃描經過外部缺陷時在缺陷邊沿處先增加隨后減小，在缺陷中心處的數值與無缺陷時相當；θ在經過內部缺陷時數值增大，而在經過外部缺陷時數值減小。

(3) 在頻率為2 000 kHz時，線圈掃描經過內部缺陷時L和Z都隨缺陷的出現迅速減小，并在缺陷處減小到最小值，線圈掃描經過外部缺陷時在缺陷邊沿處先增加隨后減小，在缺陷中心處的數值比無缺陷時的數值小；R在線圈掃描經過內外部缺陷時都明顯減小，過內部缺陷時的減小量比過外部缺陷時的減小量大；θ在線圈掃描經過內外部缺陷時其數值都增大，同樣線圈掃描經過內部時的數值增加量比過外部缺陷時的大。

(4) 通過測量頻率為200 kHz時渦流線圈經過內外部缺陷時的R和θ的變化趨勢和大小，并結合霍爾傳感器的信號能夠區分鋼板內外壁缺陷。因此，在渦流傳感器電路設計中可以將二者之一作為測量目標，并用其產生的信號作為傳感器的輸出，而線圈的L和Z的變化規律不夠明顯，不能作為傳感器的被測物理量。