基于直升機地面共振要求的起落架剛度及阻尼優化設計

吳靖，胡國才,*，柳泉，劉湘一

1. 海軍航空大學 航空基礎學院，煙臺 264001 2. 海軍航空大學 91206部隊，青島 266108

直升機起落架的剛度及阻尼對其地面狀態的動穩定性影響較大，必須確保直升機開車至起飛離地以及著陸至完全停車整個過程都不會發生地面共振，因此研究滿足地面共振穩定性要求的起落架剛度及阻尼對直升機動力學設計至關重要。

不管是陸地還是艦面[1-3]狀態，輪式或滑橇式起落架直升機[4-5]的地面共振研究通常是在已知起落架剛度及阻尼的情況下，對直升機進行地面共振分析[6-8]，驗證是否滿足穩定性要求。也有通過分析起落架剛度及阻尼對地面共振穩定性的影響，來獲得對起落架進行優化設計的有益指導[9-12]。但關于滿足直升機地面共振穩定性要求的起落架剛度及阻尼優化設計的研究較少，一般依據直升機著陸緩沖性能要求初步確定起落架剛度及阻尼，再根據地面共振要求對剛度及阻尼進行修正[13-15]；米里[16]提出以直升機滑跑時的不穩定中心與工作轉速重合，并擁有足夠阻尼裕度為要求的起落架剛度和阻尼選擇方法；顧仲權[17]提出以起落架需用阻尼最小為優化目標，主要約束條件為在給定旋翼轉速范圍內機體模態滿足阻尼裕度要求，最小模態阻尼比是通過特征值法求解模態阻尼后，在共振轉速附近尋找的方式獲得，該方法對于求解最小模態阻尼比過于繁瑣，且未考慮機體模態滿足轉速裕度要求的情況。

本文給出了機體模態非穩區臨界轉速以及與旋翼擺振后退型模態共振轉速下機體模態阻尼比的計算方法，據此提出了滿足地面共振穩定性的機體固有頻率及阻尼要求。通過建立機體模態頻率及阻尼與起落架剛度及阻尼的關系，給出了滿足地面共振穩定性的起落架剛度及阻尼要求。基于上述穩定性要求，在滿足著陸緩沖性能要求的起落架剛度及阻尼范圍內，以減小起落架需用阻尼且增大機體最小模態阻尼比為優化目標提出了對剛度及阻尼進行優化設計的方法，并對某型直升機進行了實例驗證。

1 滿足地面共振要求的機體特性

1.1 非穩區臨界轉速和共振區模態阻尼計算

在進行直升機動力學設計時，避免地面共振一般有2種方法：① 使機體模態與旋翼擺振后退型模態耦合非穩區遠離工作轉速；② 有足夠的阻尼確保耦合系統在工作轉速范圍內不會產生地面共振[13-14]。根據上述方法進行地面共振設計的關鍵是要確定非穩區臨界轉速和共振區模態阻尼。在槳轂中心有水平運動的機體模態與旋翼擺振后退型模態的共振轉速Ωr有如下關系：

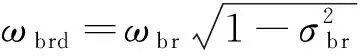
對于槳葉擺振欠阻尼情況，根據式(1a)可得共振轉速計算公式為

(2)

由于研究的是滿足直升機地面共振要求的機體特性，因此考慮旋翼槳葉擺振阻尼較大的情況，此時危險模態是機體模態，要確定其臨界轉速，就需要知道其模態阻尼在共振區附近隨旋翼轉速Ω的變化情況。由旋翼機體耦合系統的特征方程是難以解出模態阻尼的顯式表達形式，根據機體模態阻尼在非穩區附近的變化趨勢構造機體無阻尼時的模態阻尼比函數為

(3)

式中：系數A、B、C和D通過式(4)確定。

(4)

由式(4)確定的各系數為

(5)

某直升機旋翼采用黏彈減擺器來提高槳葉的擺振阻尼，在3種擺振幅值狀態下，其復模量如表1 所示。

采用式(3)計算機體無阻尼時其模態阻尼比在非穩區的變化情況，與采用特征值法求解的模態阻尼比對比如圖1所示。

表1 減擺器復模量Table 1 Complex modulus of damper

圖1 機體無阻尼時的模態阻尼比Fig.1 Modal damping ratio without fuselage damping

由圖1可知，針對槳葉不同擺振情況，式(3)均能較好地擬合機體無阻尼時其在非穩區的模態阻尼比，最大誤差為7.08%，說明了式(3)的準確性，可用于下一步確定非穩區臨界轉速。由圖1中也可以看出，隨著槳葉擺振幅值減小，黏彈減擺器儲能模量增加，擺振固有頻率增加，與機體模態耦合轉速增加，不穩定中心右移；黏彈減擺器耗能模量增加，擺振阻尼增加，機體模態阻尼增加，穩定性增加。

機體有阻尼時共振區附近的模態阻尼比為

σ(Ω)=σ0(Ω)+σfb

(6)

由式(4)和式(6)推導可知，共振點的機體模態阻尼比σ(Ωr)=(cf-cfr)/(2mfbωfb)，當cf>cfr時，即機體阻尼大于最小需用阻尼時，共振點的機體模態阻尼比大于0，也就表明機體模態不存在非穩區。

根據σ(Ω)=0可確定機體模態非穩區下界Ωl和上界Ωh分別為

(7)

采用式(7)計算機體取不同阻尼時直升機地面共振非穩區臨界轉速的變化情況，與通過特征值法確定的結果對比如圖2所示。

由圖2可知，針對槳葉不同擺振情況，式(7)均能較好地擬合機體取不同阻尼時的臨界轉速，最大誤差僅為3.54%，說明了式(7)用于計算非穩區臨界轉速的準確性。該方法避免了通過求解不同轉速下的特征值再根據特征值尋找臨界轉速的繁瑣，可為后續采用優化算法進行起落架剛度及阻尼的優化設計節省大量時間。

圖2 非穩區臨界轉速Fig.2 Critical rotation speed in instable area

1.2 機體頻率及阻尼要求

在進行直升機地面共振設計時，首先考慮是否能使機體模態與旋翼擺振后退型模態共振區遠離工作轉速，即確保機體模態非穩區下界Ωl≥ηΩmax，其中Ωmax為旋翼最大工作轉速，η為下界轉速裕度，一般取1.2[19]。

在難以使所有機體模態均滿足上述要求的情況下，可以考慮使機體低階模態非穩區上界Ωh<μΩe，其中Ωe為旋翼額定轉速，μ為上界轉速裕度，在其足夠小時，旋翼旋轉動能很小，在旋翼加速過程中就有可能通過非穩區而不會激起大幅度的振動，一般取0.4[19]。

若不能滿足上述2種情況，則需要提供足夠的阻尼確保機體模態阻尼比σ(Ω)≥ε，其中ε為阻尼裕度，一般取0.02[20]。

綜上所述，滿足地面共振穩定性的機體非穩區臨界轉速及共振點模態阻尼比的要求，即機體頻率及阻尼須滿足的要求為

(8)

滿足式(8)要求的具體判斷流程如圖3所示。

圖3 滿足穩定性要求的判斷流程Fig.3 Judgment process meeting stable requirements

2 起落架剛度及阻尼設計

2.1 機體運動特性與起落架剛度及阻尼的關系

為根據式(8)對起落架剛度和阻尼提出滿足地面共振穩定性的設計要求，需要建立起落架剛度及阻尼與機體頻率及阻尼的關系。首先，建立機體地面狀態的運動模型，支持在起落架上的機體簡圖如圖4所示。

根據分析可知，機體運動x、z和φy相互耦合，機體運動y和φx、φz相互耦合，在直升機地面共振分析中，機體縱移和橫移以及俯仰和滾轉模態較為重要，該4階模態與垂向平動和扭轉模態耦合較弱，令機體縱向運動X1=[x,φy]，機體橫向運動X2=[y,φx]，可得與地面共振相關的4階 機體模態的無阻尼自由運動方程為

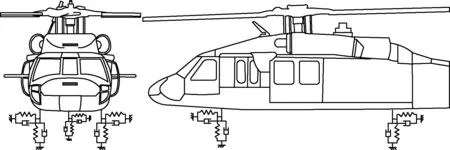
圖4 直升機簡圖Fig.4 Helicopter diagram

(9)

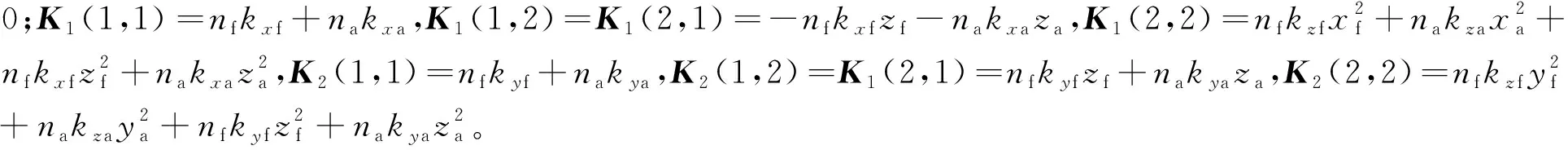
(10)

(11)

式中：ω1=[ωx,ωφy]和ω2=[ωy,ωφx]分別為機體縱向和橫向運動前2階模態固有頻率。

由于滿足地面共振穩定性的機體特性要求是根據當量至槳轂中心的平面模型得出的，因此需將機體模態質量及阻尼當量至槳轂中心，根據文獻[6,21]研究可知機體模態的瞬心位置、當量質量和當量阻尼分別為

(12)

式中：zh為重心至槳轂中心的垂向距離；z1(i)和z2(i)分別為機體縱向和橫向第i階模態瞬心距重心的垂向距離；m1(i)和m2(i)分別為機體縱向和橫向第i階模態當量至槳轂中心的質量；c1(i)和c2(i)分別為機體縱向和橫向第i階模態當量至槳轂中心的阻尼；cxf、cyf、czf和cxa、cya、cza分別為前后起落架3個方向的等效阻尼。

2.2 起落架剛度及阻尼優化方法

令剛度k=[kxf,kxa,kyf,kya,kzf,kza]，阻尼c=[cxf,cxa,cyf,cya,czf,cza]，優化目標為減小起落架的需用阻尼，且增大機體最小模態阻尼比，因此，目標函數可定義為

f(k,c)=

(13)

式中：ωbe為額定轉速下槳葉的擺振固有頻率。

基于直升機地面共振穩定性要求的起落架剛度及阻尼優化設計可描述為

(14)

式中：kmax和kmin分別為起落架剛度的上下邊界值，cmax和cmin分別為起落架阻尼的上下邊界值，由直升機著陸緩沖性能要求及具體的起落架構型確定。

嵌入尋優策略的優化流程如圖5所示，尋優策略是針對連續域的優化算法，如蟻群算法、遺傳算法或粒子群算法等，滿足的結束條件是達到最大迭代次數或目標函數值達到給定要求。

圖5 起落架剛度及阻尼的優化流程Fig.5 Optimization of landing gear stiffness and damping

3 實例仿真

實例計算中，旋翼減擺器取大擾動幅值(26 mm) 下的阻尼，旋翼主要參數如表2所示，直升機選擇小重量前后重心及大重量前后重心4種狀態，起落架采用后三點布置，不同狀態下機體及各位置參數[22]如表3所示。

以支柱式起落架為例，其縱橫向剛度主要取決于輪胎的縱橫向剛度，起落架的各向剛度為

(15)

式中：kbu為緩沖支柱等效剛度；kxt、kyt和kzt分別為輪胎3個方向上的剛度，由于前后起落架計算形式相同，式(15)以及式(16)不區分前后起落架。

根據某型輪胎剛度數據，對文獻[23]中輪胎剛度計算公式進行修改，得

(16a)

kyt=B1w(p0+0.24pr)·

(16b)

(16c)

式中：d為輪胎外徑；w為輪胎寬度；δt為輪胎垂向壓縮量；p0為輪胎充氣壓力；pr為輪胎額定充氣壓力，pr=0.25pb，pb為輪胎最小爆炸壓力；A1～A3、B1～B4和C1均為擬合系數。

表2 旋翼參數Table 2 Rotor parameters

表3 機體及位置參數Table 3 Fuselage and location parameters

針對某型輪胎，其垂向剛度確定后，根據地面平衡方程可計算其垂向壓縮量，由式(16a)可確定充氣壓力，輪胎縱橫向剛度可由式(16b)和式(16c)計算。因此，需要優化的剛度為緩沖支柱剛度及輪胎垂向剛度，k=[kfbu,kabu,kzft,kzat]，根據著陸緩沖性能要求給出各剛度范圍為：kmax=[780 900, 860 100, 1 435 900, 1 194 500] N·m-1，kmin=[254 300, 198 000, 458 800, 451 500] N·m-1。

該直升機輪胎在一定壓縮量范圍內，其當量阻尼系數與垂向壓縮量關系不大，主輪3個方向上的當量阻尼系數分別為0.188、0.125和0.204，尾輪3個 方向上的當量阻尼系數分別為0、0.205和0.237， 尾輪由于沒有剎車，不考慮其縱向剛度及阻尼。輪胎阻尼與其剛度相對應，需要優化的阻尼為緩沖支柱阻尼，c=[cfbu,cabu]，根據著陸緩沖性能要求給出各阻尼范圍為：cmax= [503 000, 1 058 800] N·s·m-1，cmin= [3 600, 2 000] N·s·m-1。

采用的優化算法為粒子群算法，種群規模為18，初始種群采取均勻隨機分布策略，迭代次數為40，各狀態下計算10次的迭代結果如圖6所示，優化所得剛度及阻尼如圖7所示。

由圖6可知，所采用的優化算法對該問題的收斂性較好，迭代40次均能收斂到最優值，直升機在4種重量重心狀態下的最優值分別為0.939 7、0.935 5、1.124 4和1.120 8。

圖6 不同重量重心下的迭代結果Fig.6 Iteration results of various weights and gravity centers

圖7 優化剛度及阻尼Fig.7 Optimized stiffness and damping

由圖7可知，4種狀態下優化所得緩沖支柱阻尼均為cmin=[3 600, 2 000] N·s·m-1，即最小緩沖支柱阻尼也能使該直升機滿足式(8)的穩定性要求。尾緩沖支柱剛度具有分散性：小重量前重心時分布于198 000～248 000 N·m-1，后重心時分布于198 000～259 000 N·m-1，大重量前重心時分布于198 000～282 000 N·m-1和703 000～860 100 N·m-1， 后重心時分布于198 000～295 000 N·m-1和760 000～ 860 100 N·m-1；主緩沖支柱剛度均為最小值254 300 N·m-1，主尾輪垂向剛度均為最大值，分別為1 435 900 N·m-1和1 194 500 N·m-1。通過分析可知，以上情況下4階模態中橫移模態阻尼比最小，為使其盡量增大，要求該階模態頻率減小且阻尼增大，這就要求主起落架垂向剛度盡可能小，而尾起落架由于距重心橫向距離為0，其垂向剛度對橫移模態沒有影響，也就出現了優化后主緩沖支柱剛度最小，而尾緩沖支柱剛度具有分散性，但不同重量重心狀態下都對應不同剛度范圍，并不是在整個優化范圍內分散，若尾緩沖支柱剛度不在上述范圍時，具有最小阻尼比的模態將會變成縱移模態，而尾起落架垂向剛度對縱移模態將會產生影響。另外，機輪垂向剛度的增加使其垂向阻尼相應增加，橫移模態阻尼也將增加，所以優化后的機輪垂向剛度達到最大。對于尾緩沖支柱剛度的選取應該使得機體橫移和縱移模態以及俯仰和滾轉模態頻率盡量分開，綜合4種重量重心狀態考慮，尾緩沖支柱剛度取小值效果較好。

因此，選取剛度k=[254 300, 198 000, 1 435 900，1 194 500] N·m-1及阻尼c=[3 600, 2 000] N·s·m-1，通過特征法計算系統模態頻率及阻尼隨轉速的變化情況，機體各模態與旋翼擺振后退型模態共振轉速及最小阻尼比如表4所示。

由表4可知，4種重量重心狀態下，機體低階模態橫移和縱移模態與旋翼擺振后退型模態的共振轉速均小于0.4Ωe=103 r/min，最小模態阻尼比均大于0，不存在非穩區，滿足式(8)中的穩定性要求；機體高階模態俯仰模態與旋翼擺振后退型模態的共振轉速位于0.4Ωe=103 r/min～1.2Ωmax=310 r/min之間，但最小模態阻尼比大于2%，滿足式(8)中的阻尼裕度要求；機體高階模態滾轉模態與旋翼擺振后退型模態的共振轉速大于1.2Ωmax=310 r/min，最小模態阻尼比大于0，不存在非穩區，滿足式(8)中的穩定性要求。

綜上，說明優化計算所得的起落架剛度及阻尼能使該直升機在4種重量重心狀態下均滿足地面共振穩定性要求。

以大重量后重心為例，通過特征法計算系統模態頻率及阻尼比隨轉速的變化情況如圖8和圖9 所示。為觀察直升機旋翼與機體耦合對系統模態的影響，圖8和圖9中 還給出了旋翼與機體非耦合時的模態頻率及阻尼，如圖8和圖9中虛線所示。

由圖8和圖9可知，直升機旋翼與機體的耦合會使系統各模態頻率及阻尼發生變化，在旋翼擺振后退型模態與機體模態共振轉速附近，模態阻尼會發生相互“排斥”的現象，使得其中阻尼較小的模態阻尼降低，若模態阻尼在旋翼機體耦合因素的影響下降低至負值，則會引發系統的地面共振動不穩定現象。

表4 共振轉速及最小阻尼比

圖8 大重量后重心時的模態頻率Fig.8 Modal frequencies with large weight and back gravity center

圖9 大重量后重心時的模態阻尼比Fig.9 Modal damping ratio with large weight and back gravity center

需要注意的是低轉速(Ω<150 r/min)時，旋翼擺振后退型和前進型模態頻率無法分開，而該2階模態阻尼卻呈現較大差異，該現象可通過獨立旋翼運動方程的特征值[19]解釋：

(17)

旋翼低轉速時，如果槳葉擺振剛度較小，而擺振阻尼較大，就會形成過阻尼的情況，上述特征值將變為

(18)

由式(18)的特征值虛部可知，在上述情況下，旋翼擺振后退型及前進型模態頻率均等于旋翼轉速Ω，考慮旋翼與機體耦合的影響后，結果會有一定差異，如圖8所示；而由特征值實部可知，擺振阻尼的增加，可能會使得低轉速時的擺振后退型模態阻尼降低，如圖9中的擺振后退型模態阻尼在低轉速時就比較小。但是，隨著轉速增大，槳葉擺振固有頻率會增加，且由于減擺器非線性的影響，在相同幅值擾動下，擺振阻尼會降低，這都會使得擺振后退型與前進型模態頻率逐漸分開，特征值由式(18)回歸式(17)。

4 結 論

1) 針對機體無阻尼時構造的非穩區機體模態阻尼比函數能較好地擬合槳葉不同擺振狀態下機體模態阻尼比隨轉速的變化，據此給出了機體模態非穩區臨界轉速的計算方法，由該方法計算機體不同阻尼情況下的臨界轉速，最大誤差僅為3.54%，說明了該方法的準確性。

2) 基于直升機地面共振穩定性要求，提出了對起落架剛度及阻尼進行優化設計的方法，采用該方法對某直升機4種重量重心狀態下起落架的剛度及阻尼進行優化，結果使得機體各階模態均滿足地面共振穩定性要求：機體橫移和縱移模態與旋翼擺振后退型模態的共振轉速均小于0.4Ωe，最小模態阻尼比均大于0；機體俯仰模態與旋翼擺振后退型模態的共振轉速位于0.4Ωe～1.2Ωmax之間，但最小模態阻尼比大于2%；機體滾轉模態與旋翼擺振后退型模態的共振轉速大于1.2Ωmax，最小模態阻尼比大于0。