PLRD-(k,m):保護鏈接關系的分布式k-度-m-標簽匿名方法*

張曉琳，何曉玉，張換香，李卓麟

內蒙古科技大學 信息工程學院，內蒙古 包頭 014010

1 引言

隨著互聯網技術的快速發展，社會網絡分析在眾多領域獲得廣泛關注和應用。社會網絡分析需要將網絡數據發布給第三方，由于社會網絡數據包含用戶的隱私信息，如何在發布數據的同時保護用戶的隱私信息成為研究的熱點。社會網絡通常被表示成簡單圖，圖中的節點和邊分別對應社會網絡中的個體以及個體間的聯系，個體的屬性信息，如年齡則表示成節點的標簽，如圖1所示。

Fig.1 Social network graphG圖1 社會網絡原始圖G

重識別(re-identification)攻擊[1]，是指攻擊者通過與攻擊目標相關的背景知識(如度、鄰居子圖等)，從網絡中識別出目標的過程。為了抵抗重識別攻擊，研究者提出了不同的社會網絡圖匿名化技術，通過修改圖結構防止隱私信息泄露，如k-degree匿名[2]。現實中，攻擊者能夠很輕易地獲取到與目標相關的多種背景知識，簡單地通過修改圖結構并不能很好地保護個體的隱私。

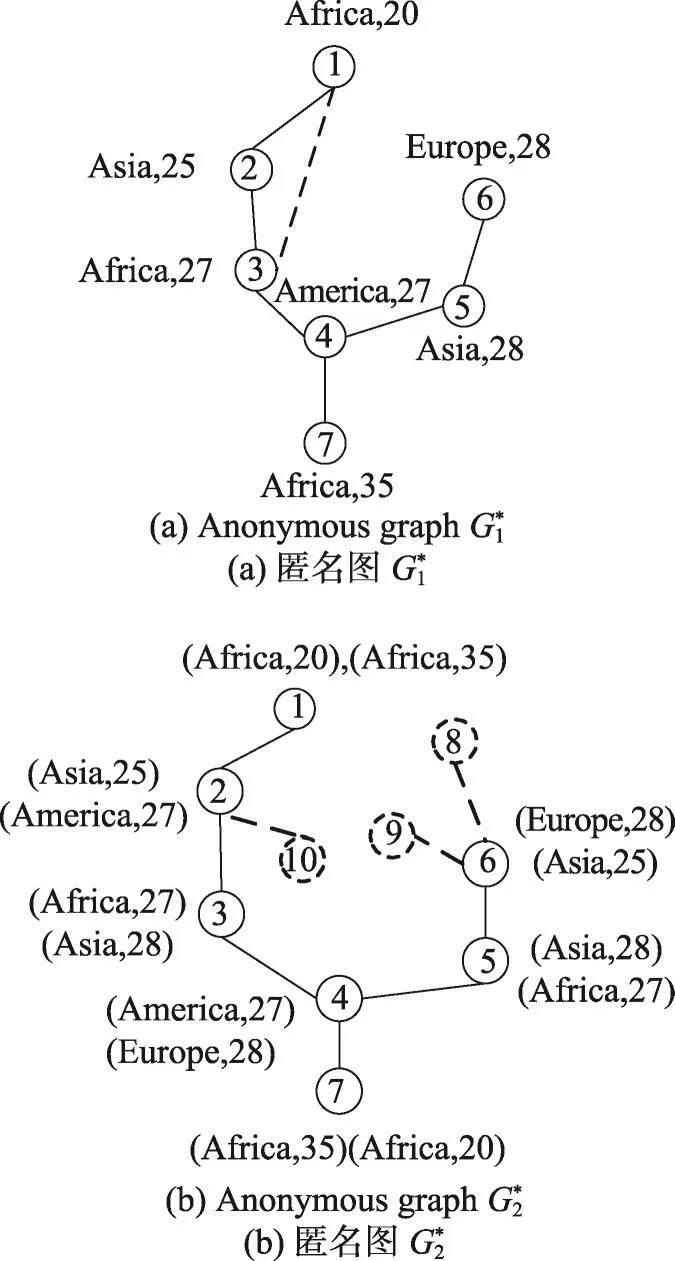
Fig.2 Two anonymized versions forG圖2 圖G的兩個匿名圖

為此，提出一種分布式社會網絡匿名方法，目的是在提高處理大規模社會網絡效率的同時，得到匿名圖，如圖2（b）所示。在圖中，即使攻擊者獲知節點的度和標簽，也無法準確推測出被攻擊者的身份及鏈接關系。例如攻擊者獲知Bob在社會網絡中擁有3個朋友，27歲且來自America，圖中節點2和4均符合條件，則攻擊者準確識別出Bob的概率不大于1/2，且由于節點2和4不存在鏈接，攻擊者也無法推測出Bob的鏈接關系。

2 相關工作

隨著在線社會網絡的發展和普及，社會網絡隱私信息的安全性成為研究學者關注的熱點，并提出了多種保護方法。文獻[4]引入屬性-社交網絡模型將屬性信息視作節點，通過分割節點屬性鏈接和社交鏈接保護用戶隱私。文獻[5]提出一種基于kdegree匿名的隱私保護模型SimilarGraph，采用動態規劃的方法對節點進行最優簇劃分，在保護隱私的同時保持社會網絡圖結構性質。文獻[6]提出一種kweighted-degree匿名方法，在匿名圖中，對任意節點，至少存在（k-1）個其他節點與其度相同且在閾值t范圍內具有相同的權重序列。文獻[7]提出一種utilityaware匿名方法，在進行k-degree匿名時同時考慮最短路徑和鄰居節點重疊程度，提高了匿名圖的數據可用性。文獻[8]指出即使個體的身份信息被有效隱藏，攻擊者仍能推測出個體的鏈接關系，為此設計了一種L-opacity匿名模型，通過opacity矩陣在保護個體身份的同時保護鏈接關系。文獻[9]將用戶交互社會網絡抽象成二分圖模型，通過為用戶產生一個標簽列表的方式抵抗重識別攻擊。文獻[10]針對敏感鏈接關系設計一個LinkMirage模型，模糊社會網絡圖中的社交拓撲結構并提供帶有模糊社交關系視圖的不受信任的外部應用，從而抵抗重識別攻擊。文獻[11]提出添加偽節點，并在真實節點和偽節點間添加邊的k-degree匿名方法。文獻[12-13]提出了基于社區的圖匿名模型，在k-degree匿名的同時，提高匿名圖的數據可用性。文獻[14]提出一種基于單變量微聚合的k-degree匿名方案，通過建立差矩陣Mp×2提高數據的可用性。文獻[15]提出了基于SMC（secure multi-party computation）模型的隱私保護方案，“數據代理”通過分布匿名協議實現標簽屬性和存儲位置的l-diversity匿名。文獻[16]提出一種基于SMC模型的semi-honest的交換加密技術，保護隱私信息。文獻[17]提出基于MapReduce模型的隱私保護方案，通過兩個階段實現k-匿名。文獻[18-19]則利用Map-Reduce框架在大規模圖中檢索同構子圖。

可以看出，目前的隱私保護技術多關注匿名數據的可用性，忽略了攻擊者可能具有多種背景知識的情況。此外，現有的分布式隱私保護技術針對的是關系型數據，未考慮個體在社會網絡中的圖性質特征，不能很好地保護個體的隱私，并且MapReduce將中間結果存放于磁盤，處理過程中需要反復遷移數據，并不適合處理圖數據。為此，提出一種分布式匿名方法 PLRD-（k,m）（distributedk-degree-m-label anonymity with protecting link relationships），該方法基于GraphX系統[20-21]，在保護隱私的同時提高算法的執行效率。

3 背景知識及問題定義

社會網絡表示成節點帶標簽的簡單無向圖G=(V,E,L,δ)，其中節點集V代表社會網絡中的用戶，E是邊集合代表用戶間的聯系，社會網絡中個體的屬性信息用節點標簽L表示，函數δ表示節點與標簽之間的映射δ:V→L。

定義1（標簽鏈接泄露）已知G*是社會網絡圖G=(V,E,L,δ)的匿名圖，C是攻擊者通過標簽信息得到的一組節點，對?u∈C，?v∈C，若攻擊者能以一定概率推測出u、v存在鏈接，則稱C存在標簽鏈接泄露。

以圖2（a）為例，攻擊者通過目標27歲，得到節點3和4，此時，能推測節點3和4存在鏈接，因此{3,4}存在標簽鏈接泄露。

定義2（PLR-（k,m）匿名）已知G*是社會網絡圖G=(V,E,L,δ)的匿名圖，若圖G*是PLR-（k,m）匿名，則滿足：

（1）圖G*是k-degree匿名圖，即攻擊者通過節點的度，識別出目標節點的概率不大于1/k。

（2）圖G*是m-標簽匿名圖，即攻擊者通過節點標簽，識別出目標節點的概率不大于1/m。

（3）匿名圖G*不存在標簽鏈接泄露。

定義3（最大缺失值）已知社會網絡圖G=(V,E,L,δ)，Ci(i=1,2,…,k)是包含k個節點的分組，且Ci∧Ci+1=? ，Δi是分組Ci內節點度最大值與最小值的差，若M是最大缺失值，則M=max{Δ1,Δ2,…,Δi,Δi+1,…,Δn}[11]。

以圖1為例，若分組C1={3,5,1,7},C2={4,2,6}，則此時最大缺失值M=max{(2-1),(3-1)}=2。

定義4（無向完全圖）若圖G={V,E}是無向完全圖，則滿足條件：

?u∈V,?v∈V?(u,v)∈E

4 分布式隱私保護算法PLRD-(k,m)

GraphX是Spark上用于圖和并行圖計算的處理系統，編程模型上遵循“節點為中心”模式，計算過程由若干順序執行的超級步（superstep）組成，在超級步S中，節點匯總從超級步(S-1)中其他節點傳遞過來的消息，改變自身的狀態，并向其他節點發送消息，消息經過同步后，會在超級步(S+1)中被其他節點接收并做出處理。同時，GraphX引入了擴展自Spark RDD的屬性圖，并提供了一組基本功能操作，如圖構造操作、圖反轉等，以及優化的PregelAPI。

4.1 分布式節點分組算法FUG

為了滿足定義2中的條件（3），提出一個節點安全分組條件SGC（safety grouping condition）。若設C是包含k個節點的分組，若分組C滿足SGC，則對?u∈C,?v∈C，兩節點的最短路徑長度應滿足dist(u,v)≥2。

定理1已知社會網絡圖G=(V,E,L,δ)，C是節點集V中k個節點構成的分組，dist(u,v)表示節點u、v的最短路徑長度，若?u∈C，?v∈C，滿足dist(u,v)≥ 2，則分組C不存在鏈接。

證明反證法。假設分組C存在鏈接，則分組C內必存在節點u、v滿足條件dist(u,v)=1，這與?u∈C，?v∈C，滿足dist(u,v)≥2相矛盾，假設不成立，故定理1成立。

基于定理1和模塊化社區發現的思想[22]，提出一種分布式節點分組算法FUG（fast unfolding of group），基本步驟如下：

（1）初始化，為節點添加分組信息groupid，將節點劃分在不同的分組。

（2）節點搜索2-hop鄰居，并修改groupid合并分組。

（3）構建新圖，新圖中的節點是步驟（2）產生的不同分組。

重復步驟（2）和（3），直至構建的新圖是完全圖，程序結束。FUG算法分為兩個階段（phase），如圖3。圖3中，圓圈內數字是groupid，花括號內數字是分組所包含的節點（nodeid）。

Fig.3 Fast unfolding of group圖3 FUG算法

由圖3可以看出，在Phase1階段，節點搜索2-hop鄰居，并修改groupid合并分組，而Phase2階段則構建新圖并進入下一輪迭代。

定理2已知社會網絡圖G=(V,E,L,δ)，對 ?u∈V，?v∈V，dist(u,v)表示節點u和v的最短路徑長度，v滿足v∈{s|s∈V∧dist(u,s)=1}，w∈V且w∈{z|z∈V∧dist(v,z)=1}，若w是u的2-hop鄰居節點，即dist(u,w)=2，則節點w滿足：

w∈{g|g∈V∧g≠u∧dist(u,g)≠ 1}

證明反證法。假設節點w不是節點u的2-hop節點，則u、w的關系分為三種情形：（1）dist(u,w)≥2；（2）u=w；（3）dist(u,w)=1。若情形（1）成立，由題設v∈{s|s∈V∧dist(u,s)=1}，則dist(v,w)＞1，這與w∈{z|z∈V∧dist(v,z)=1}矛盾，故情形（1）不成立；若（2）和（3）成立，則與w∈{g|g∈V∧g≠u∧dist(u,g)≠1}相矛盾，故（2）和（3）不成立。綜上所述，假設不成立，節點w是節點u的2-hop鄰居節點。□

基于定理2，利用GraphX系統通過兩次迭代,節點便能搜索到2-hop鄰居節點。第一次迭代，節點向鄰居節點發送groupid，收到消息的節點生成1-hop鄰居列表；第二次迭代，節點將1-hop鄰居列表發送給鄰居節點，收到消息的節點遍歷列表，依據定理2生成2-hop鄰居列表，具體如算法1所示。

算法1搜索2-hop鄰居

Input：messages.

Output：The list of 2-hop neighborhood of vertexu.

1.THNList;//初始化2-hop鄰居節點列表

2.longstep=getsuperstep();//取出超級步

3.ifstep==0 then

4.for each vertexudo

5.sendMessToNeighbors(vertext.groupid);//超級步為0時，節點發送groupid給鄰居節點

6.else ifstep==1 then

7.longneighborhoodlist=getValue(messages);//取出消息，生成1-hop鄰居節點列表

8.sendMessToNeighbors(neighborhoodlist);//發送1-hop鄰居列表給鄰居節點

9.else ifstep==2 then

10.for each message do//處理所有1-hop鄰居節點列表

11.if the groupid in messages meet the conditions{groupid≠u.groupid}∧{groupid?u.neighborhoodlist}

12.THNList←groupid;//添加2-hop鄰居列表

13.returnTHNList;

以圖1為例，算法1如圖4所示。為了便于表述，圖中省略了nodeid，僅標出了groupid。

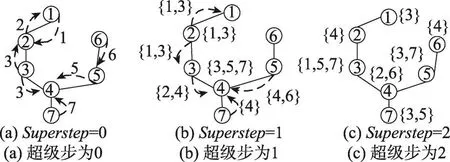
Fig.4 2-hop neighbor search圖4 2-hop鄰居搜索

當superstep=0時，節點向鄰居節點發送自己的groupid，如圖4（a）；當superstep=1時，節點收到消息后生成1-hop鄰居列表，并將列表轉發給鄰居節點，例如節點2根據消息1和3，生成列表{1,3}，并將{1,3}轉發給鄰居節點，如圖4（b）；當superstep=2 時，收到消息的節點遍歷所收到的列表，依據定理2產生2-hop鄰居列表，例如節點4收到列表{2,4}，{4}和{4,6}，依據定理2，排除1-hop列表{3,5,7}和自身groupid=4，則THNList={2,6}，如圖4（c）。

從圖4（c）可以看出，若隨機修改groupid，可能無法合并分組。以3、5、7為例，若3修改為5，5修改為7，7修改為3，此時分組未發生變化。為此，提出一種W&N（will-negotiation）策略。在W&N策略中，節點是鄰居節點的“調解人”，如圖5（a），節點4是節點3和5的“調解人”，思想是：

（1）節點u從2-hop鄰居列表中選出最小的groupid，連同自身groupid以（u.groupid,u.min）形式發送給“調解人”。

（2）若消息存在節點u和v滿足：u.groupid=v.min∧v.groupid=u.min，則“調解人”返回（u.groupid,v.groupid）給節點u、v。

（3）節點u、v收到消息后，將自身groupid修改為（u.groupid,v.groupid）中最小的值。

具體如算法2所示。

算法2Group merge

Input：messages.

1.longstep=getsuperstep();//取出超級步

2.ifstep==0 then

3.for each vertexudo

4.longu.min=getMinValue(THNList);//選擇最小groupid

5.sendMessToNeighbors((u.groupid,u.min));//節點u發送(u.groupid,u.min)給“調解人”

6.else ifstep==1 then

7.longmergerlist=getValue(messages);

8.if IsExist(u.groupid=v.minandv.groupid=u.min)IN mergerlist then

9.sendMessToNeighbors(u.groupid,v.groupid);//“調解人”返回消息給鄰居節點

10.else ifstep==2 then

11.u.groupid=min{u.groupid,v.groupid};//修改groupid

以圖1為例，算法2如圖5所示。當superstep=0時，節點從2-hop鄰居列表中選出最小groupid，并以（u.groupid,u.min.groupid）的形式發送給“調解人”，如圖5（a）；當superstep=1時，“調解人”判斷是否轉發消息，例如節點2滿足算法第8行，則轉發{(3,1)(1,3)}給節點1和3，如圖5（b）；當superstep=2 時，算法執行第11行，節點3將自身groupid修改為groupid=1，節點4修改為groupid=2，如圖5（c）。

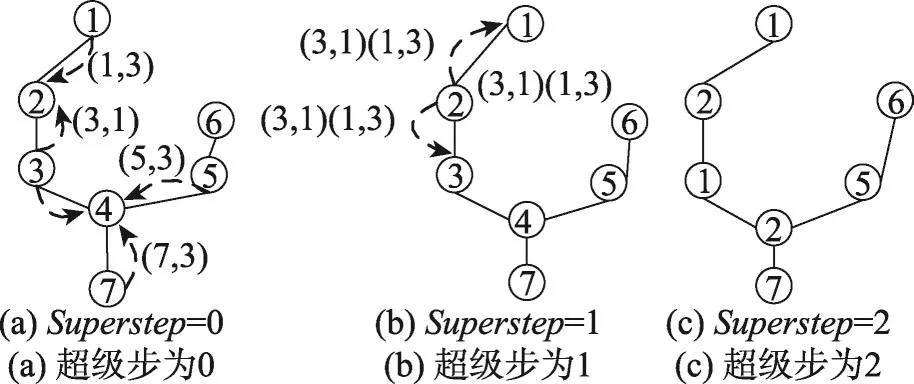
Fig.5 Grouping merged圖5 分組合并

由圖3可知，在Phase1結束后，FUG算法轉入Phase2階段構造新圖，使用RDD（resilient distributed datasets）很方便實現。FUG算法將當前圖的邊信息＜srcid,dstid＞保存在edgeRdd。節點的nodeid和相應的groupid信息，以 ＜nodeid,groupid＞的形式保存在groupRdd，然后執行兩次leffOuterJoin操作得到新圖的邊信息，最后通過GraphX系統的Graph.fromEdge-Tuples從新圖的邊信息后構建出新圖，首次構建的新圖如圖3（c）所示。

如此，經過3次循環迭代，圖G的最終分組結果為：group1={1,3,5,7}和group2={2,4,6}。

4.2 分布式k-degree匿名

為了不向分組引入鏈接，k-degree匿名采用添加節點和邊的方式實現，并要求添加的邊(u,v)滿足條件：u∈V∧v∈V*，其中V*是添加的節點集，而V*中節點的數目可以通過式（1）得出[11]。

其中，k是分組中節點數目，M是最大缺失值。

定理3FUG算法收斂，且當算法收斂時，構建的新圖Gn是無向完全圖。

證明反證法。（1）假設Gn是無向完全圖時，FUG未收斂。根據定義4，在圖Gn中，任意節點u和v，滿足dist(u,v)=1，由算法1，此時節點u和v轉變為InActive狀態，FUG算法收斂，假設不成立。（2）假設FUG算法收斂時，圖Gn不是無向完全圖，由定義4可知，此時圖Gn中，存在節點u和v滿足dist(u,v)≥2，節點仍處于Active狀態，FUG算法會繼續執行，未收斂，假設不成立。綜上所述，定理3成立。

由于Gn是完全圖，節點彼此間可以通信，因此通過GraphX可以很容易地計算出最大缺失值M。節點分組時，FUG算法并未考慮參數k。因此，計算M值時，首先要對4.1節產生的分組進行分割，方法是：將分組節點按度值降序排列，每k個節點劃分成一個子分組（subgroup），若最后一個子分組節點數目不足k，則與前一個子分組合并。計算最大缺失值M的步驟如下：

（1）初始化，分組劃分成若干子分組，子分組計算subi=|dmax-dmin|，即節點度最大值與最小值的差，令M=max{sub1,sub2,…,subn} 。

（2）superstep%2=0時，發送M值給鄰居節點。

（3）superstep%2=1時，節點將消息對比自身M值。若大于自身值，則更新為收到的M值，保持Active狀態，否則轉為InActive狀態。

（4）重復（2）（3），直至節點處于InActive狀態。

具體如算法3所示。

算法3Computing max deficiency

Input：messages,k.

Output：Max deficiencyM.

1.Initialization;//初始化，將group劃分成若干subgroup，并計算M值

2.longstep=getsuperstep();//取出超級步

3.ifstep%2==0 then

4.sendMessToNeighbors(M);//發送M給鄰居節點

5.ifstep%2==1 then

6.longValue=getValue(messages);//取出M值

7.ifValue＞M;

8.setM=Value;//更新自己的M值

9.else

10.voteToHalt();//轉為InActive狀態

11.returnM;

以4.1節產生的分組{5,3,1,7}和{2,4,6}為例，并假設k=2，算法3如圖6。初始化時，分組{5,3,1,7}被劃分為子分組{5,3}和{1,7}，并計算sub1={5,3}=0，sub2={1,7}=0，因此分組{5,3,1,7}相應的M值為0，同理{2,4,6}的M值為2。當superstep=0時，節點處于Active狀態并向鄰居節點發送值M，如圖6（b）；當supertep=1時，節點將消息對比自身M值，若大于自身值則更新并保持Active狀態，反之轉為InActive狀態，如圖6（c），節點1將M值更新為2，并保持Active狀態，而節點2轉為InActive狀態。最終，得出最大缺失值M=2。

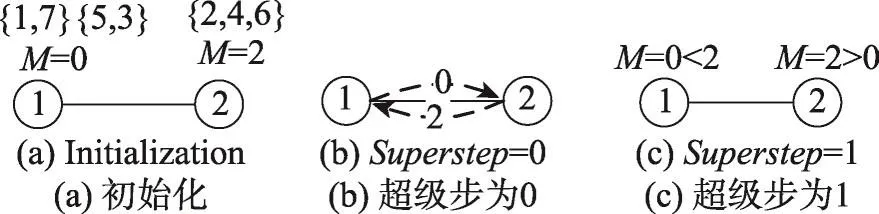
Fig.6 Computing max deficiency圖6 計算M值

分組內節點不存在鏈接，不能通過傳遞消息確定目標度。因此，為分組創建相應的虛擬節點作為“中樞”，其鄰接節點是分組內的各個節點，如圖7（a）所示。分組節點與虛擬節點構成二分圖結構，兩者通過消息傳遞，經過3個superstep完成k-degree匿名，基本步驟如下：

（1）superstep=0時，分組節點為Active狀態，并發送（nodeid,degree）給虛擬節點，其中nodeid是節點的編號，degree是節點的度。

（2）superstep=1時，虛擬節點為Active狀態，對分組節點按度降序排列，并令最大度為目標度，計算Δdi和num，Δdi是節點vi要添加的邊的數目，num是節點vi前i-1個節點添加邊的總數目，發送（vir.id,Δdi,num）給分組節點，vir.id是虛擬節點的編號（vir.id=0,1,2…）。

（3）superstep=2時，分組節點收到消息后，利用參數vir.id、Δdi、num以及k、M添加偽邊。方法是：利用式（1）計算添加節點數目N；然后建立Δdi×2的矩陣，矩陣的第0列是節點的nodeid，第1列按行依次寫入pesudo[(vir.id+num+X)modN]，其中X={1,2,…,Δdi}；最后以（nodeid,pesudo[i]）的形式將矩陣存入edgeRDD。

Fig.7k-degree anonymity圖7 k-degree匿名

具體如算法4所示。

算法4Generate pseudo edge

Input：messages,k,M.

Output：the pseudo edge list ofu.

1.PseudoedgeList←? ;

2.longstep=getsuperstep();

3.ifstep==0 then

4.for each vertexudo

5.if isLeft()then

6.sendMessToNeighbors((vertext.nodeid,vertext.degree));//節點發送消息給虛擬節點

7.if step==1 then

8.if notisLeft()then

9.longList=getValue(messages);//取出消息

10.Set max degree as target degree;//設置目標度

11.for every nodeuin List

12.ComputingΔdi、num;//節點計算Δdi、num

13.sendMessToNeighbors(virid,Δdi,num);

14.ifstep==2 then

15.if isLeft()then

16.Add pseudoedge(nodeid,pesudo[i]);//添加偽邊

17.returnPseudoedgeList；

以算法3產生的分組{1,7}、{5,3}、{2,4,6}為例，算法4如圖7所示。當superstep=0時，分組節點向虛擬節點發送nodeid和度，如圖7（a）。當superstep=1時，虛擬節點找出目標度，并為節點計算Δdi和num。以虛擬節點1為例，并假設節點降序排列為{4,2,6}，則目標度為3，節點2前一個節點是節點4，則Δdi=(3-2)=1，num=0，故返回消息（1,1,0)，同理節點6，Δdi=(3-1)=2，num=0+1=1，故返回消息（1,2,1)，如圖7（b）。當superstep=2時，分組節點根據消息以及N添加偽邊，以分組{4,2,6}為例，節點 2消息為（1,1,0），則(vir.id+num+X) modN=(1+0+1）mod3=2，添加邊（2,pseudo[2])，節點6根據消息（1,2,1），依次添加偽邊（6,pseudo[(1+1+1)mod3])，即偽邊（6,pseudo[0]）以及偽邊（6,pseudo[(1+1+2)mod 3])，即（6,pseudo[1]）。

添加的偽邊信息被保存到edgeRDD中，然后通過Graph.fromEdgeTuples操作從edgeRDD構建出包含N個偽節點的匿名圖，用8、9、10替換pseudo[i]（i=0,1,2），匿名圖如圖2（b）所示，并且N個偽節點的度為d或(d+1)，具體證明請參考文獻[11]。

4.3 分布式m-標簽匿名

m-標簽匿名采用統一標簽列表匿名[9]，其生成的方法是：假設C是由算法3產生的含有k個節點的分組，p={p0,p1,…,pm-1}是整數序列{0,1,2,…,k-1}的子集，其大小為m(m≤k)，對 ?v∈C，u表示節點v的標簽列表，則其統一標簽列表由式（2）產生：

以分組{2,4,6}為例，其相應的標簽列表分組為{u2,u4,u6}，并假設m=2,p=(0,1)，則經過式（2）統一列表為：u2={u2,u4},u4={u4,u6},u6={u6,u2}。

分析式（2）可知，利用4.2節的方法很容易實現分布式m-標簽匿名，方法步驟如下：

（1）superstep=0，分組節點發送消息（nodeid,labellist）給虛擬節點。

（2）superstep=1，虛擬節點收到消息，根據式（2）為分組節點產生統一標簽列表，并將匿名結果返回給分組節點。

（3）superstep=2，分組節點收到消息后，將原有標簽列表修改為范化標簽列表。

算法5Generate lable list

Input：messages.

1.longstep=getSuperstep()；

2.ifstep==0 then

3.for each vertexudo

4.if isLeft()then

5.sendMessToNeighbors((u.nodeid，u.labellist));//節點向虛擬節點發送(nodeid,labellist)

6.ifstep==1 then

7.if notisLeft()then

8.longlist=getValue(messages);//虛擬節點取出消息

9.for vertextuin list do

10.new=(u.nodeid，u.genlabellist);//標簽匿名

11.sendMessToNeighbors(new);//虛擬節點向用戶節點返回新的標簽

12.ifstep==2 then

13.if isLeft()then

14.longAnolabel=getValue(message);

15.setValue(Anolabel);//節點u修改自身標簽

以圖1為例，并假設m=2，p={0,1}，為了便于表述，節點i的標簽用ui來表示，則分組{1,7}、{5,3}、{2,4,6}對應的標簽分組為 {u1,u7}、{u5,u3}、{u2,u4,u6}。當superstep=0時，分組節點向虛擬節點發送消息（nodeid,labelist），如圖8（a）；superstep=1時，虛擬節點利用式（2）為分組節點產生統一標簽列表，并返回給分組節點，如圖8（b）；當superstep=2時，分組節點收到消息后，將自身的標簽替換成統一標簽列表，如圖8（c）所示。

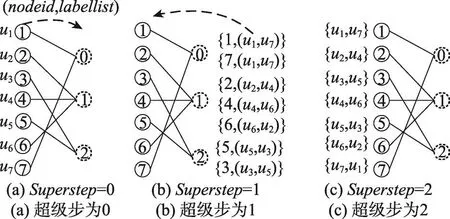
Fig.8 Label anonymity圖8 標簽匿名

5 擴展的PLRD-(k,m)方法

社會網絡中，用戶對隱私保護強度具有不同的需求，某些用戶甚至不希望隱藏自己的身份，如公眾名人[23]。基于同一標準對用戶進行匿名保護，不僅會增加匿名成本，還將降低匿名數據的可用性。為此，對PLRD-(k,m)方法進行擴展，提出個性化匿名方法PLRDPA（protecting link relationships distributed personalized anonymity)，為用戶提供lv0～lv2不同的隱私保護級別。

lv0級：隱私保護級別為0，即對用戶的信息不做任何匿名處理。

lv1級：隱私保護級別為1，能夠抵抗攻擊者通過度信息識別用戶身份和鏈接關系。

lv2級：隱私保護級別為2，攻擊者即使擁有節點的度和標簽，也無法識別出用戶身份和鏈接關系。

若通過FUG算法進行分組，不同隱私保護級別的節點可能被分在同一組。為此，提出個性化安全分組條件PSGC（personalized safety grouping condition）。設C是包含k個節點的分組，若分組C滿足PSGC條件，則：

（1）?u∈C，?u∈C?u.lv=v.lv

（2）?u∈C，?u∈C?dist(u,v)≥2

條件1表明同一分組的節點具有相同的隱私保護等級；條件2表明同一分組的節點彼此間的最短路徑長度dist(u,v)≥2。因此對算法2做出適當修改以滿足PSGC條件，“調解人”判斷的條件修改為：

（1）u.groupid=v.min

（2）v.groupid=u.min

（3）u.lv=v.lv

算法3計算M值時，隱私級別為lv0的分組將M值置為0。經過算法2和算法3，對隱私保護級別為lv1的分組利用算法4進行k-degree匿名；隱私級別為lv2的分組，只需要在lv1的基礎上執行算法5即可。

6 PLRD-(k,m)方法的安全性分析

PLRD-(k,m)方法的目標是抵抗節點重識別的同時，抵抗標簽鏈接泄露，對算法安全性的分析從這兩方面著手。

定理4已知圖G*是社會網絡圖G=(V,E,L,δ)，由PLRD-(k,m)生成的匿名圖，P是攻擊者根據節點的度或標簽從G*中識別出目標節點的概率，則概率P滿足：1/k≤P≤1/m。

證明（1）若攻擊者僅掌握了節點的度，由于G*是k-degree匿名圖，對任意節點v存在(k-1)個其他節點與v的度相同，則節點v被識別出的概率為1/k。（2）若攻擊者僅掌握了節點v的標簽，由算法5，在匿名圖G*中存在(m-1)個其他節點包含v的標簽，故被識別的概率為1/m。（3）若攻擊者同時掌握了節點v的度信息和標簽信息，由概率組合知識可知，節點v被識別的概率為1/m。

定理5已知圖G*是社會網絡圖G=(V,E,L,δ)，由PLRD-(k,m)生成的匿名圖，則圖G*不存在標簽鏈接泄露。

PLRD-(k,m)方法包括FUG、k-degree匿名以及m-標簽匿名，分析可知，k-degree匿名和m-標簽匿名均不會導致標簽鏈接泄露。因此，只需證明FUG算法不會將鏈接引入分組。

證明每次迭代，FUG算法都要構建新圖，用Gi表示第i次構建的圖，Si表示圖Gi中的節點，由算法1和算法2可知，節點Si是由圖Gi-1中互為2-hop鄰居的節點u、v形成的超級節點，故節點Si在Gi中的鏈接關系繼承自節點u、v，即u、v在圖Gi-1中的1-hop鄰居節點，在Gi中轉變為節點Si的1-hop鄰居節點。因此，FUG算法不會將鏈接引入分組。

7 實驗分析

實驗對PLRD-(k,m)隱私保護方法進行性能分析和評價，采用真實社會網絡com-Youtube圖數據集。com-Youtube圖數據集包含1 134 890個節點和2 897 624條邊。由于PLRD-(k,m)方法涉及到節點標簽而com-Youtube數據集不包含標簽信息，因此實驗中人工生成節點標簽信息。節點的標簽包括3個屬性：國籍（80個國家）、性別（男或女）、年齡（15～75）。所有的值滿足同一分布。為了進行對比，實驗同時在單工作站環境實現了PLRD-(k,m)和PLRDPA方法，兩種環境如下：

單工作站環境：Intel Core i7-2720QM，CPU 2.2 GHz，16 GB RAM；操作系統，Win 7 旗艦版；編程語言，Python。

集群環境：12臺計算節點搭建的集群，Hadoop 2.7.2，Spark1.6.3；CPU 1.8 GHz，16 GB RAM，編程語言，Scala。

其中，PLRD-(k,m)和PLRDPA算法所對應的單工作站版本分別記作PLR-(k,m)和PLRPA。在實現PLRPA和PLRDPA時，實驗從數據集中虛擬出10%的節點為lv0級，15%的節點為lv2級，剩余節點則將隱私級別設置為lv1級。

7.1 算法性能分析

7.1.1 運行時間

圖9展示了算法隨閾值m變化的運行時間對比結果。從圖9可以看出，隨著m值的增大運行時間隨之增大，原因是m值越大，序列p={p0,p1,…,pm-1} 的范圍越廣，m-標簽匿名消耗的時間越多。同時，從實驗結果也可以看出，PLRD-(k,m)和PLRDPA算法的匿名開銷要遠小于PLR-(k,m)和PLRPA，所提出的算法在處理大規模數據上更具有優勢。

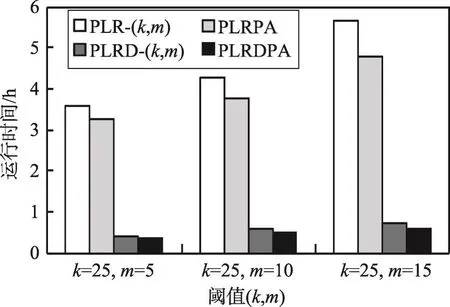
Fig.9 Comparison of run time圖9 運行時間對比

7.1.2 加速比和規模可擴展性

相對加速比是指同一并行算法在單個計算節點上運行時間與在多個相同計算節點構成的處理系統上運行時間之比，其計算公式如下：

計算節點的數目從3逐步增加到12，并將數目為3時的運行時間作為T(1)，結果如圖10所示。可以看出，兩種算法均具有良好的加速比，但不是理想的線性加速比，因為隨著計算節點數目的遞增，彼此間的通信量會隨之增多，產生更多的額外開銷。

實驗通過固定計算節點數目，擴大數據規模并求處理時間比的方法評測算法的擴展性，可擴展性計算公式如下：

Fig.10 Speedup ratio圖10 加速比

式中，DB是基礎數據集，m×DB是m比例于DB的數據集，T(*)是處理數據集消耗的時間。實驗將com-Youtube圖數據集等分成5份，然后按1∶2∶3∶4∶5重新聚合成split1～split5，并將數據集split1作為基礎數據集DB，然后在集群上處理5個數據集，實驗對比結果如圖11所示。根據式（4），理想狀態下，Scalability的值應不大于比例m，但圖12表明，處理split5時，Scalability的值卻大于5，原因是受限于CPU的處理能力以及I/O消耗。

Fig.11 Scalability圖11 可擴展性

7.2 數據可用性分析

PLRD-(k,m)方法修改了圖的結構和節點屬性值，因此，實驗通過計算圖結構信息的損失和查詢的準確性來評價算法在數據可用性上的表現。

7.2.1 圖結構信息損失

實驗通過平均最短路徑長度和聚集系數的變化率來評測匿名圖G*的信息損失。節點u的聚集系數是指其鄰居節點中連接關系所占的比例。圖結構信息變化率定義為|G-G*|/|G|，其中G和G*分別表示在原始圖和匿名圖中的測量值，Error值越小，數據的可用性越好。圖12和圖13分別顯示了匿名圖在平均最短路徑長度、聚集系數的變化情況。從實驗結果可以看出，隨著分組中節點數目的增加，匿名后圖結構信息的損失率也相對增加。

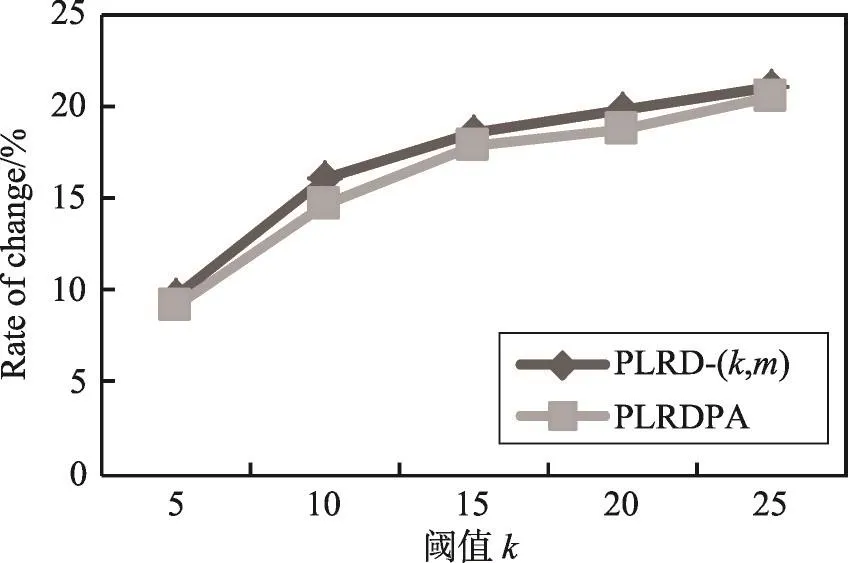
Fig.12 Change ratio of average shortest path圖12 平均最短路徑變化率

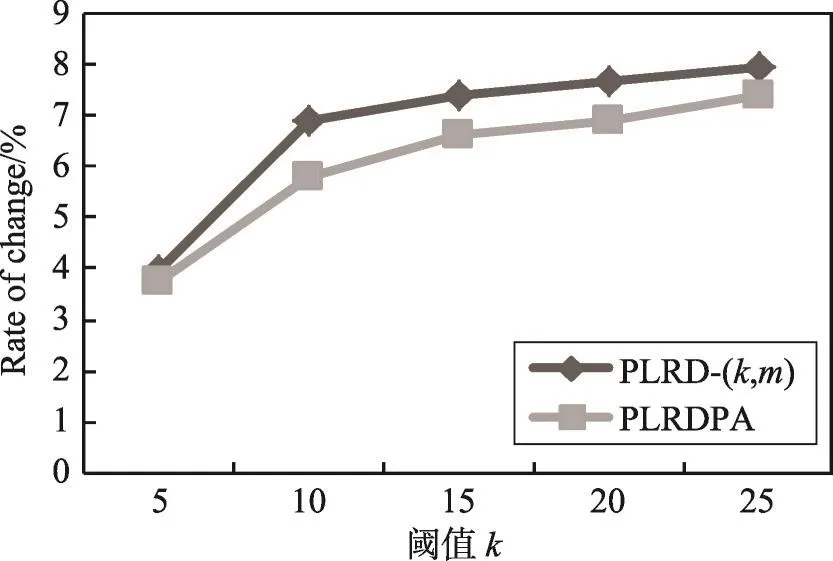
Fig.13 Change ratio of clustering coefficient圖13 聚集系數變化率

7.2.2 查詢準確性

實驗采用文獻[9]所提出的單跳查詢和雙跳查詢評測查詢準確性，并用相對誤差率作為度量標準。相對誤差計算公式為|N-N*|/N，其中N表示原始圖數據上的查詢結果，N*表示匿名圖數據上查詢結果。實驗采用不同的屬性進行多次查詢，然后計算誤差率取平均值。

實驗通過單跳查詢評測PLRD-(k,m)方法在查詢準確性上的表現，并對比PLRDPA方法。實驗提出的查詢操作為：“在不同年齡段，A國用戶和B國用戶間存在多少朋友關系”。圖14展示了不同閾值對算法PLRD-(k,m)和PLRDPA查詢結果的影響。實驗結果表明，在閾值參數相同的情況下，相比于PLRD-(k,m)方法，PLRDPA方法的查詢誤差更低，說明根據用戶不同需求，提供個性化匿名保護能夠更好地保護數據的可用性。

Fig.14 Relative error of query圖14 查詢誤差率

圖15和圖16分別展示了參數k對單跳查詢、雙跳查詢的準確性的影響。實驗結果表明，隨著分組中節點數目的增加，查詢誤差率隨之增大，因為分組中節點數目越多，節點的候選標簽數越多，因此導致查詢結果的相對誤差變大。同時表明，個性化匿名的查詢誤差率明顯更低，能夠更好地保護查詢準確性。

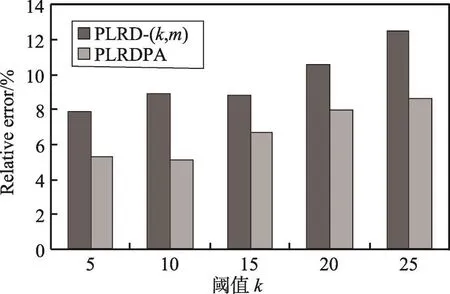
Fig.15 Relative error of single-hop query圖15 單跳查詢誤差率

8 結束語

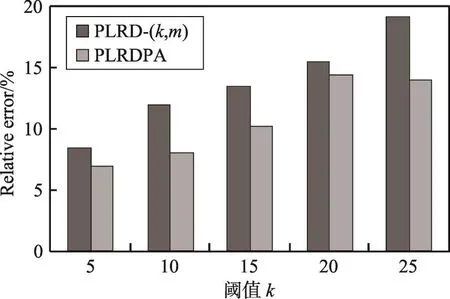
Fig.16 Relative error of dual-hop query圖16 雙跳查詢誤差率

目前的隱私保護技術僅針對某一種背景知識，并且隨著社會網絡規模的逐年遞增已不能滿足實際需求。為此，提出一種分布式匿名方法PLRD-(k,m)，該方法基于GraphX“節點為中心”的特點，將互為N-hop鄰居的節點分為一組，并對分組進行k-degree匿名和m-標簽匿名，在抵抗重識別攻擊的同時保護了鏈接關系。此外，為了滿足個性化需求，擴展了PLRD-(k,m)方法，提出一種個性化匿名方案PLRDPA，允許用戶設置不同的隱私級別并提供不同的保護。基于真實社會網絡的實驗數據表明，所提出的算法能夠在提供隱私保護的同時，提高處理大規模數據的效率。

社會網絡中，受限于身份的不同，用戶在輿論傳播過程中具有不同的影響力。匿名社會網絡時，往往需要對圖結構進行一定程度的修改，很可能導致匿名前后用戶的影響力發生重大變化。因此接下來將考慮在匿名社會網絡圖的過程中保護節點的影響力。