壓縮打捆機構及曲柄模態與諧響應分析

郭振華，陳換美

（1.石河子大學機械電氣工程學院，石河子 832000；2.巴音郭楞職業技術學院）

0 引言

我國具有豐富的蘆葦等粗纖維資源，可用于造紙、建材、飼料、醫藥等行業[1]。然而，由于蘆葦密度低，致使其運輸成本較高，愿意承擔蘆葦運輸的車輛很少。蘆葦打捆裝備可以有效解決蘆葦等原料運輸過程中產生的虧噸問題，對降低企業生產成本具有非常重要的作用。但是，在打捆裝備的工作過程中，機械振動不可避免。打捆機構在一定的振動頻率范圍內容易產生共振現象，這會導致關鍵構件發生結構損傷，進而影響對蘆葦的壓縮效果。本文針對打捆機的核心機構——壓縮曲柄滑塊機構及曲柄進行模態分析和諧響應分析，為打捆機的設計提供理論參考。

1 模態分析理論

模態分析是將系統的振動微分方程組中的物理坐標變換為模態坐標，通過方程組解耦，求出系統的模態參數，使其成為用模態坐標和模態參數描述的獨立方程[2]。

式（1）為N自由度的線性振動表達式。式中 [M]——系統的質量矩陣；[C]——系統的阻尼矩陣；[K]——系統的剛性矩陣；——系統加速度——速度；x ——位移；F（t）——系統激振力。

模態分析分為自由模態分析和約束模態分析。自由模態是指在不考慮任何約束的情況下，得到的系統本身固有特性。自由模態是模態分析的重要組成部分，通過自由模態分析，可以對系統自身的尺寸、材料、振動等固有特性有必要了解。約束模態則是指系統在受約束情況下的模態分析[2]。

對系統進行自由模態分析時，設定系統在振動時不受外力，即 F（t）=0。此時，系統內部阻尼較小，在分析系統自由振動的頻率和振型時可忽略不計。得到系統無阻尼振動微分方程：

該方程特解為：

式（3）中，Φ表示自由響應幅值矩陣。

將式（3）代入式（2）中，可得特征方程：

式（4）中，ωi表示第 i階固有頻率。

經過上述變換，將系統固有頻率和振型問題轉變成求解方程特征值問題。方程（4）有非零解的充要條件為：

應用分塊蘭索斯法（Block Lanczos）將方程（5）變換為對角矩陣，采用追趕法求解，可得n個不同正解ωoi（i=1，2,…n）。

ωoi表示系統第i階固有頻率。

2 壓縮曲柄滑塊機構模態仿真分析

偏置式曲柄滑塊機構是壓縮打捆機核心部件，該部件的剛度、強度及其力學特性決定整機的使用壽命。通過對打捆機曲柄滑塊機構進行有限元模態分析，得出其在工作狀態下的固有頻率和振型，可以為避免共振現象的產生提供數據支持。

2.1 建立有限元模型

有限元分析軟件abaqus自帶三維建模功能，但是建模過程繁瑣，并且精度較低。為提高建模效率，應用專業三維建模軟件solidworks對壓縮曲柄滑塊機構進行建模，然后將建好的三維模型導入abaqus中進行分析。建模過程中，為減少計算時間提高分析效率，可以在不影響分析效果的前提下對模型進行簡化，如：忽略圓角倒角等對有限元分析結果影響不大的結構特征。

具體步驟如下：

（1）應用三維軟件建立打捆機曲柄滑塊機構的三維模型；

（2）將建成的三維模型另存為Para solid格式，并導入abaqus軟件中；

（3）在abaqus環境下設置模型材料，具體設置如表1所示：

表1 40Cr材料屬性

（4）劃分網格：網格劃分類型采用0.008 mm四面體，結果如圖1。

圖1 壓縮曲柄滑塊機構的網格劃分圖

（5）對網格劃分結果進行檢測，結果如表2，表明網格劃分結果滿足模態分析要求。

表2 材料屬性

2.2 仿真結果及分析

模態分析提取階數設置為5階，擴展階數設置為5階，頻率區間設置為0～3 000 Hz。

在上述參數設置下，對曲柄滑塊機構進行約束模態分析，仿真結果如下：

前5階固有頻率和振型描述如表3所示：

分析結果可知：

（1）在前5階模態仿真結果中，1階模態和2階模態固有頻率為為0或近似為0，可認為結構基本無變形，表現為剛性。

（2）3階至5階的模態云圖表明，曲柄滑塊機構發生明顯的變形和位移。其中，曲柄的變形較明顯，故對曲柄進行單獨的模態分析。

圖2 模態云圖第3階

圖3 模態振型云圖第4階

圖4 模態振型云圖第5階

表3 前5階固有頻率和振型描述

3 壓縮曲柄的模態仿真分析

通過對曲柄進行網格劃分和模態分析，得到曲柄的5階約束模態云圖，結果如圖5至圖9所示：

圖5 模態云圖第1階

曲柄的5階模態分析云圖描述如表4。

通過上述分析可知，曲柄的5階模態固有頻率分別為 6.71Hz、19.68Hz、28.89Hz、116.73Hz、255.63Hz。為避免共振現象的發生，在打捆機工作狀態下，應避免出現上述頻率。

打捆機的工作頻率可由式（7）表達。

式中 f——激振頻率；n——動力輸出軸轉速；δ——誤差系數。

圖6 模態云圖第2階

圖7 模態云圖第3階

圖8 模態云圖第4階

圖9 模態云圖第5階

表4 曲柄前5階模態描述

通過式（7）可求得不同頻率下對應的輸出軸轉速，如表5所示。

表5 轉速對應表

根據國家標準，拖拉機動力輸出軸轉速范圍為540～1 000 r/min。對應表5，為避免共振現象的產生，發動機轉速應盡量避免540.5～640.5 r/min和816.6～916.6 r/min兩個轉速范圍內使用。

4 諧響應分析

諧響應分析用于確定線性結構在承受隨時間按正弦（簡諧）規律變化的載荷時的穩態響應，分析過程中只計算結構的穩態受迫振動，不考慮激振開始時的瞬態振動。諧響應分析的目的在于計算出結構在幾種頻率下的響應值對頻率的曲線，從而能預測結構的持續性動力特性，驗證設計是否能克服共振、疲勞以及其他受迫振動引起的有害效果[2,6,8]。壓縮打捆機曲柄的模態分析反映了系統本身的振動屬性，諧響應分析可以反映其在實際工作環境下的振動響應。

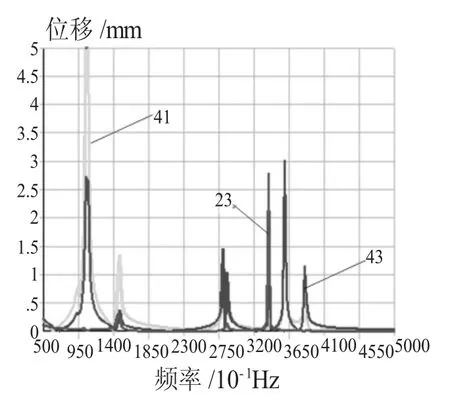
圖10 Y平面內諧響應分析云圖

4.1 諧響應參數設置

通過模態分析可以得到壓縮曲柄滑塊機構曲柄的固有頻率范圍為0～256 Hz，因此，選取0～500 Hz為機構的激振范圍，設置載荷步為200，在曲柄端施加幅值為3000N的簡諧載荷。根據所得的約束模態振型，提取3處關鍵點進行響應分析，分別取機構中關鍵點23、41、43。關鍵點的位移響應如圖10和圖11所示。

4.2 仿真結果及分析

通過對響應云圖10和圖11的分析可知：當振動頻率為100.81Hz、126.11Hz、278.6Hz、321.93Hz（舍去）、350.35Hz（舍去）時，曲柄易發生共振現象。其中，最大諧峰值出現在第4階和第5階。可見，在壓縮打捆機工作過程中，不同的振動頻率將會產生不同振幅，振幅過大會影響壓縮效果，甚至對設備造成一定的破壞。

圖11 Z平面內諧響應分析云圖

5 小結

本文通過對壓縮打捆機曲柄滑塊機構及曲柄進行模態分析和諧響應分析得到以下結論：

（1）曲柄滑塊機構的前5階模態中，1階和2階模態表現為剛性，3階至5階模態中曲柄滑塊機構表現出明顯的位移和變形，其中曲柄表現較明顯。

（2）曲柄的5階模態固有頻率分別為6.71 Hz、19.68 Hz、28.89 Hz、116.73 Hz、255.63 Hz，在固有頻率下曲柄的上下端面易發生變形，5階模態下發生扭曲變形。為避免共振現象的產生，發動機轉速應避免在 540.5～640.5 r/min和 816.6～916.6 r/min兩個轉速范圍內使用。

（3）諧響應分析表明，當振動頻率為100.81 Hz、126.11 Hz、278.6 Hz時，曲柄將發生共振現象。其中，最大諧峰值出現在第4階和第5階。