非參數回歸的貝葉斯估計

蘇雅玲,何幼樺

(上海大學理學院,上海200444)

在回歸分析中,相對于回歸函數形式已知的參數回歸,非參數回歸的函數形式自由,受約束少,回歸模型完全由數據驅動.對于非參數回歸問題,已經有很多學者進行了研究,目前回歸函數的非參數估計主要集中在核估計、局部多項式估計、樣條函數以及小波估計.如Devroye[1]證明了回歸函數核估計的強相合性.Greblicki等[2]和Devroye[3]在不同條件下證明了回歸函數核估計的逐點相合性.Fan[4]引入局部線性回歸估計并闡述其優越性,給出了估計量的均方誤差(mean-square error,MSE)和積分均方誤差(mean integrated square error,MISE),并研究了估計量的最大最小效.Antoniadis等[5]引入回歸函數的小波估計,并證明了估計量的相合性和漸進正態性.上述方法單純從數據本身出發,沒有充分利用數據以外的信息,雖然能夠達到較好的擬合效果,但是外推效果較差.

在參數估計問題中,貝葉斯方法已經得到廣泛的應用,而在非參數估計問題中,貝葉斯方法是從Ferguson[6]在1973年發表了論文A Bayesian Analysis of Some Nonparametric Problems[6]后才開始受到關注.Ferguson給出了當總體X 的分布函數F(x)的先驗為Dirichlet過程時,F(x)的非參數貝葉斯估計為F(x)先驗分布與經驗分布的加權平均.此外,Jayaram[7]提出了拓展的Dirichlet過程先驗.在此基礎上姚宗靜[8]給出簡單Dirichlet過程的構造性定義,討論了其性質和支撐問題,求出在該先驗下后驗分布的具體表達形式.也有學者將非參數貝葉斯方法應用到回歸函數的估計中,如龍杏芬等[9]在局部線性估計中窗寬h的先驗分布為Gamma分布的條件下,基于貝葉斯方法構造了回歸函數的局部線性估計,并給出窗寬和回歸函數的后驗分布和抽樣方法,通過數值模擬驗證了貝葉斯局部線性估計方法的可行性.盧一強等[10]對廣義非參數模型B樣條貝葉斯估計進行了研究,給出了回歸函數B樣條貝葉斯估計的馬爾科夫鏈蒙特卡洛(Markov chain Monte Carlo,MCMC)模擬計算方法.

本工作針對非參數回歸模型,在Ferguson給出的總體分布函數的貝葉斯估計基礎上,進一步得到一個光滑的條件分布估計.基于該分布最終構造出回歸函數的貝葉斯估計,并研究該估計的收斂性質,給出該估計中超參數的合理表達式.最后,通過實證分析將非參數貝葉斯方法與局部線性回歸進行了比較.

1 非參數回歸的貝葉斯估計

文獻[6]給出了總體X的分布函數F(x)的非參數貝葉斯估計,在該估計中取F(x)的先驗分布服從Dirichlet過程.Dirichlet過程定義如下.

定義1 設X為一樣本空間,A是X的子集構成的σ代數,α＞0,P0為(X,A)上的有限非零測度.如果對 X 的任意可測分割 A1,A2,···,Am,p=(P(A1),P(A2),···,P(Am))服從參數為α =(αP0(A1),αP0(A2),···,αP0(Am)) 的 Dirichlet分布,則稱p是(X,A)上參數為 α,基測度為P0的Dirichlet過程,記為p～DP(α,P0).

文獻[6]中的Dirichlet過程即為DP(α,P0),α為正實數,記F0(x)=P0{X ≤x}是先驗過程的期望(均值函數).則在樣本為x1,x2,···,xn時,F(x)的貝葉斯估計為

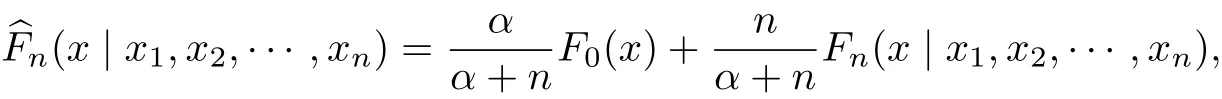
該估計是先驗過程的期望分布F0(x)和經驗分布估計Fn(x|x1,x2,···,xn)的加權平均.由于經驗分布函數是階梯函數,為得到一個光滑的分布估計,用核估計代替經驗分布函數Fn(x|x1,x2,···,xn),則總體的密度估計為

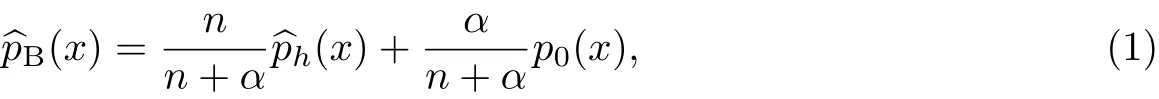
現考慮Y∈R1對X=(X1,X2,···,Xd)∈Rd的多元非參數回歸模型

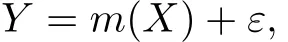
其中m(X)是未知回歸函數,ε是均值為0方差為σ2的誤差項.設(x,y)是變量(X,Y)的某個具體取值,{(Xi,Yi),i=1,2,···,n}為樣本數據.在多維情況下,式(1)可表示成如下形式:

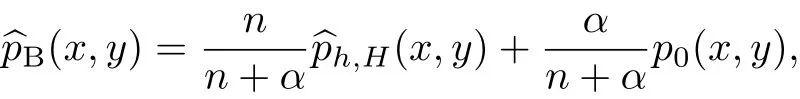
Y的條件分布的貝葉斯估計為

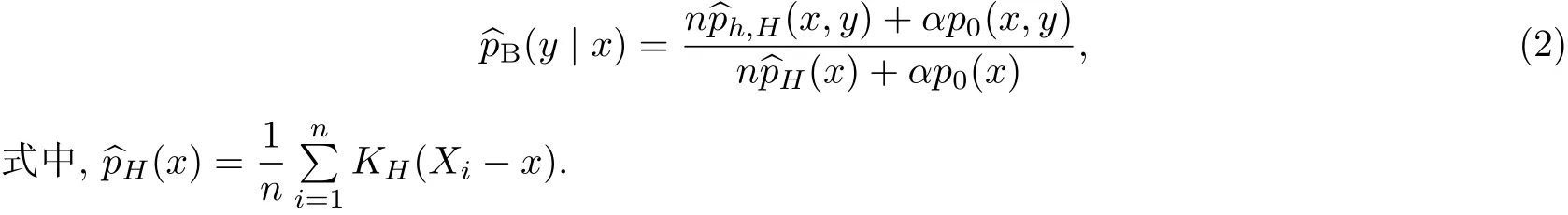
在二次損失下,回歸函數m(x)的貝葉斯估計為

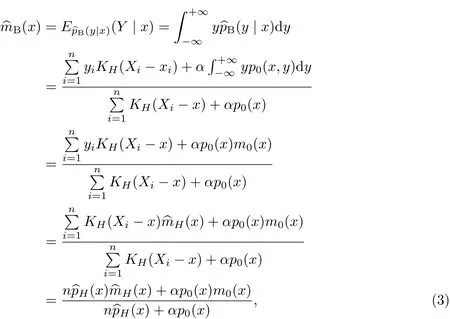
式中,m0(x)為m(x)基于p0(x,y)的先驗回歸函數Nadaraya-Watson核回歸估計,即零階局部多項式回歸.考慮一階局部多項式回歸(局部線性回歸)將會減少邊界偏倚,而不增加方差[11],因此在計算中可以將式(3)中的多元Nadaraya-Watson核回歸估計 ^mH(x)替換成多元局部線性回歸估計

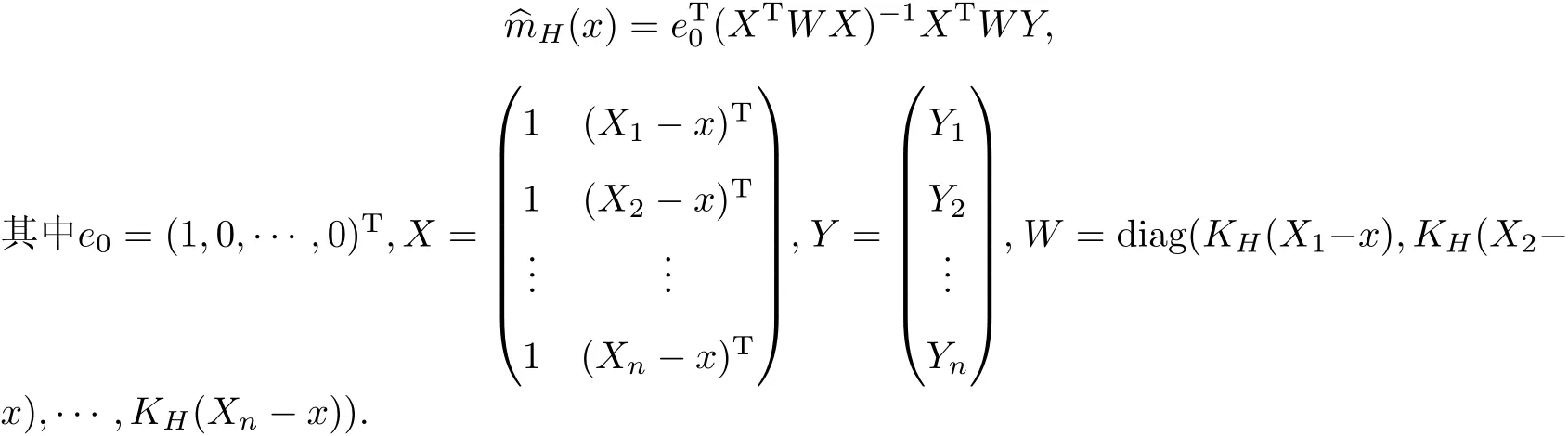
另一方面,m(x)的貝葉斯估計式(3)中,α反映 ^mB(x)對先驗m0(x)的依賴程度,如果這種依賴隨x的變化而有所不同,則式(3)可寫成

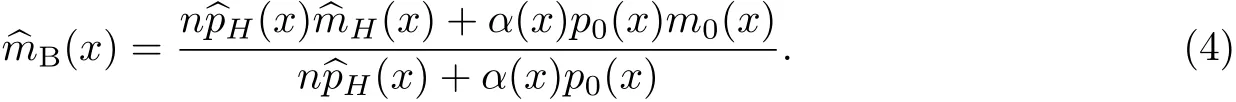
1.1 估計的均方收斂性

文獻[12]給出了多元局部線性回歸估計 ^mH(x)的方差和偏差.

引理 1 對于樣本模型Yi=m(Xi)+εi,i=1,2,···,n.^mH(x)為m(x)具有帶寬矩陣H的局部線性估計,并滿足文獻[13]中的正則條件.設x為一個非邊界點,則在給定X1,X2,···,Xn下^mH的偏倚為

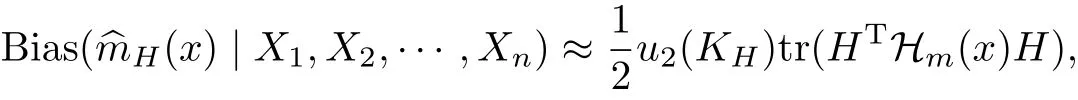
這里Hm(x)為m(x)的Hessian矩陣,而u2(KH)是核函數KH的二階矩.^mH的方差為

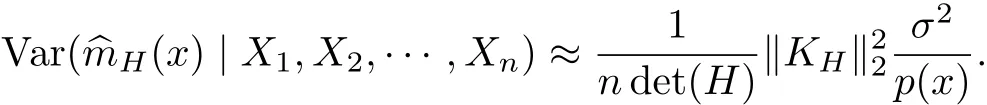
記Var(^mH(x))=Vn(x),Bias(^mH(x))=E(^mH(x))-m(x)=Bn(x),則m(x)核估計^mH(x)的均方誤差為

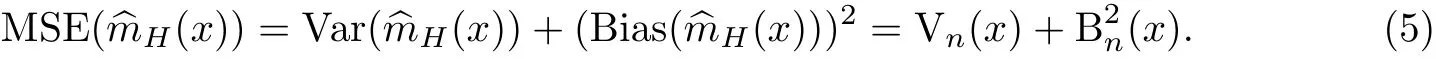
定理1 在^mH(x)滿足引理1的條件下,m(x)的貝葉斯估計的均方誤差為

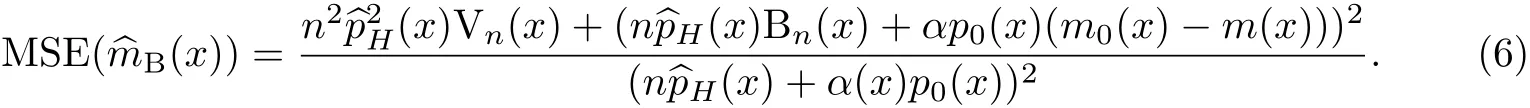
注意到,當m0(x)=m(x)時,

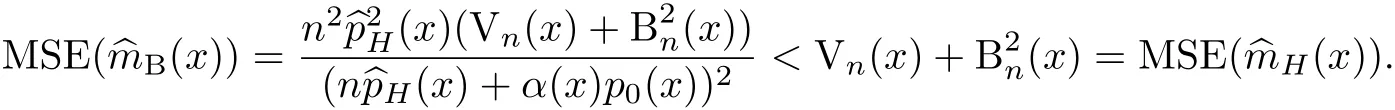
由此可知,當m(x)先驗選擇接近m(x)時,m(x)的非參數貝葉斯估計的均方誤差將小于其局部線性回歸估計的均方誤差.

1.2 超參數α(x)的確定

式(4)中的超參數α(x)反映了分布估計對先驗分布的依賴程度,α(x)越大則這種依賴越強.在實際計算時,需要對超參數α(x)進行合理地確定.

定理2 以MSE達到最小的α(x)可以表示為

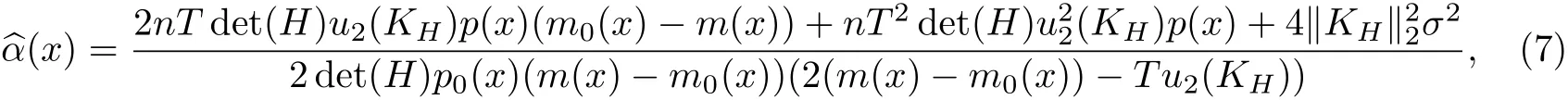
其中T=tr(HTHm(x)H).

證明

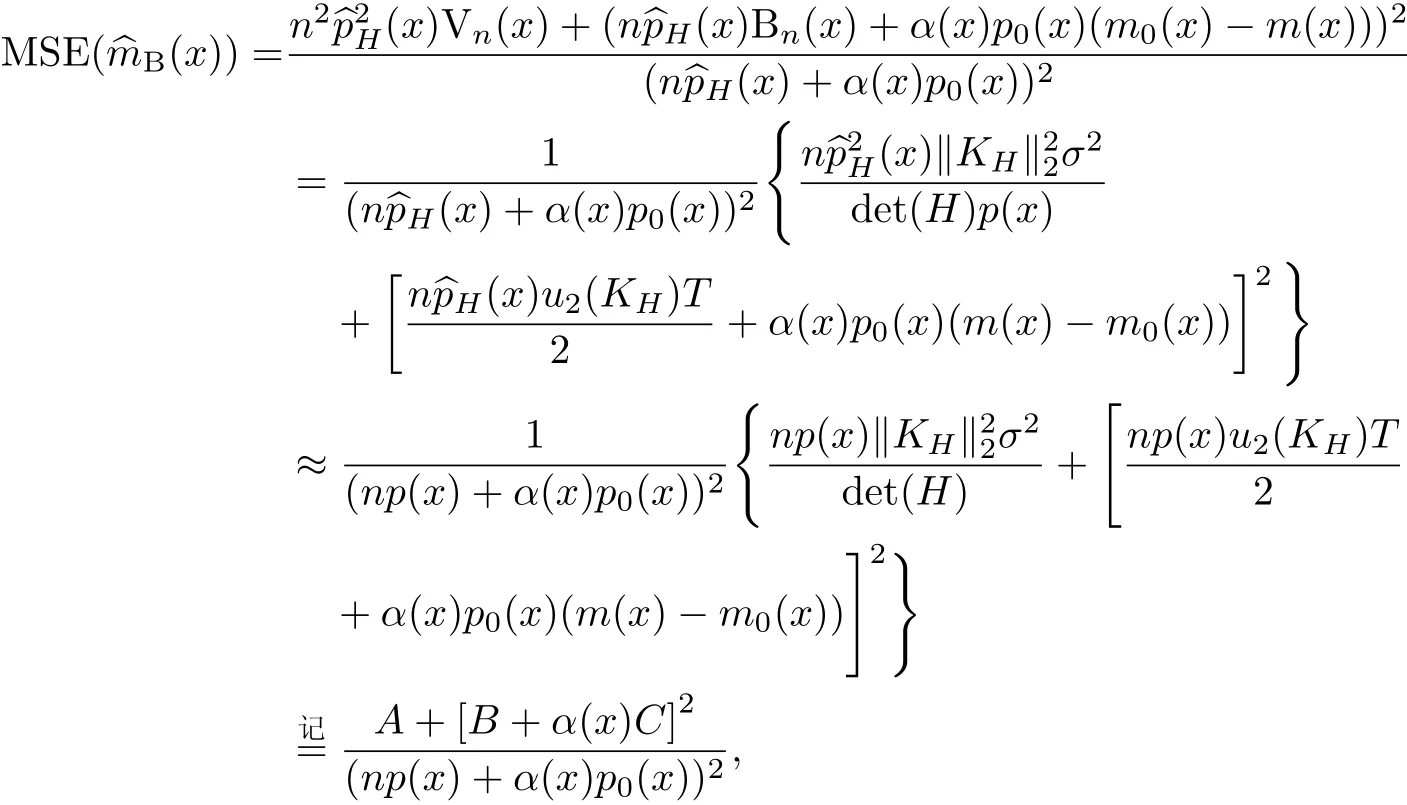
其中

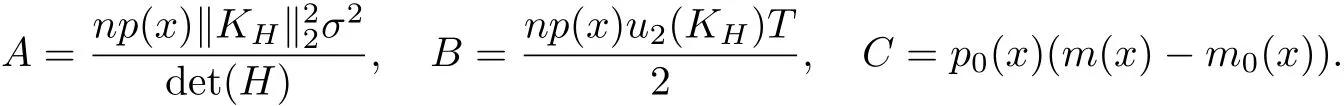
上述約等式中是用p(x)代替了核估計^pH(x).

MSE(^mB(x))關于α(x)的一階偏導數為

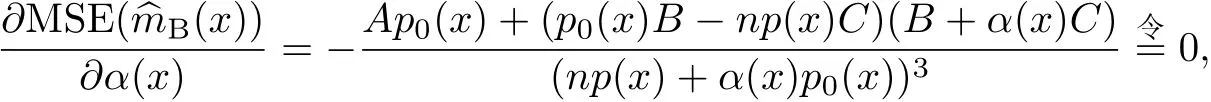
得式(7)的結果.又因α(x)為式(7)時

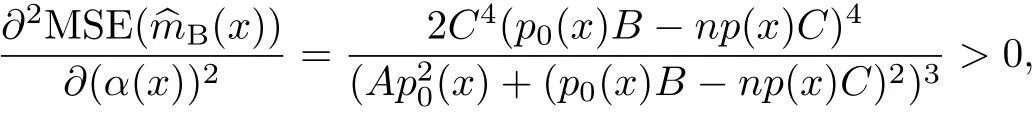
所以當α(x)取式(7)時,MSE(^mB(x))取得極小值.

在定理2中,當m(x)對每個分量的二階偏導接近0,即T≈0時,則可取

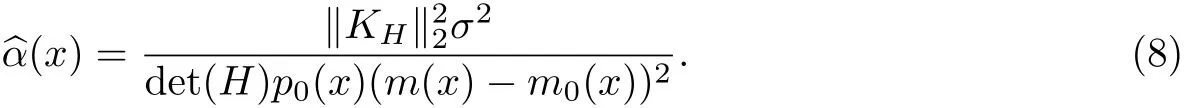
根據式(8)可知,當先驗回歸函數的選取和真實的回歸函數接近時,(m(x)-m0(x))2較小,^α(x)較大,回歸函數的非參數貝葉斯估計結果對先驗分布依賴度高.反之,當先驗回歸函數的選取和真實的回歸函數相差較大時,^α(x)較小,則估計結果對先驗分布依賴度較低.由于m(x)是未知的,先驗m0(x)的選取具有主觀性,因此可以限定(m(x)-m0(x))2≤M,M為正實數.式(8)中α(x)的確定還依賴方差σ2,其估計可采用文獻[11]中的方法.

2 實證分析

為了檢驗所提出算法的有效性,本工作以人口預測問題作為實證分析,樣本選取1990—2005年的中國人口數據,建立人口數量對時間的回歸模型,運用非參數貝葉斯方法對模型進行估計,最后以2006—2010年的數據檢驗模型,并將結果與局部線性回歸進行對比分析.

2.1 人口模型的估計

基于1990—2005年的中國人口樣本建立一元非參數回歸模型:

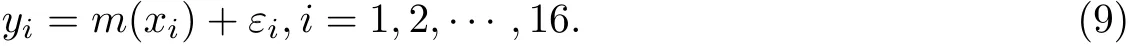
選取Logistics人口模型[14]作為先驗:

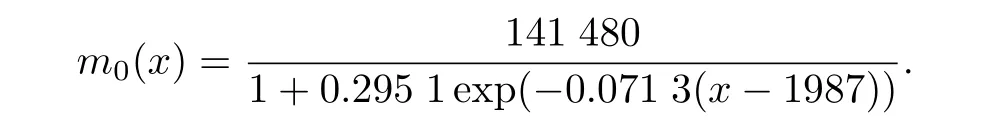
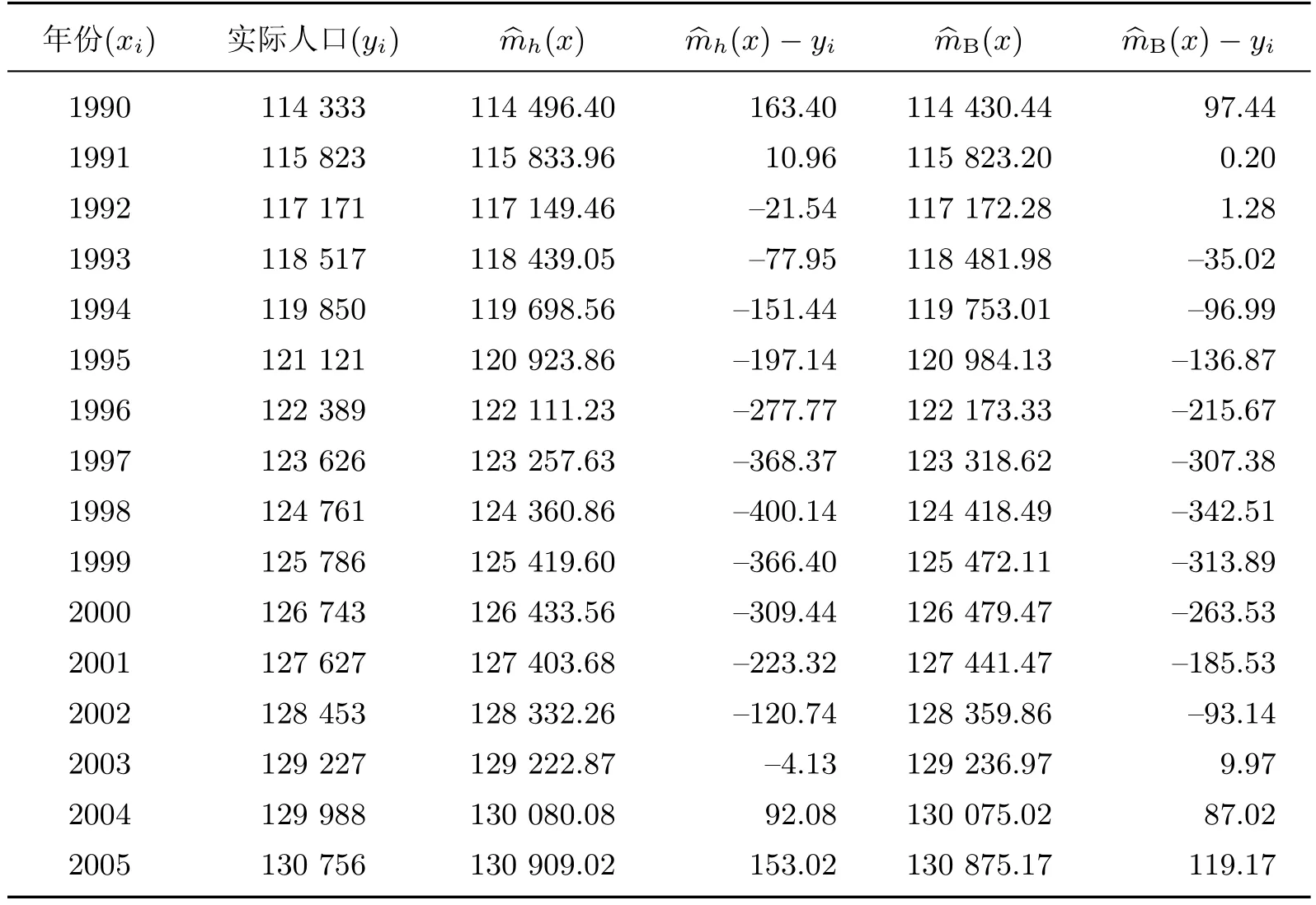
表1 1990—2005年中國人口數量估計結果Table 1 Estimation of China's population in 1990—2005 萬人

表2 擬合均方誤差MSETable 2 Fitting mean square error MSE萬人

由表2可以看出,非參數貝葉斯估計與局部線性回歸方法相比較,均方誤差要小得多,擬合效果較好.

2.2 人口模型的預測

由2.1節得到人口數量的非參數貝葉斯估計結果,預測2006—2010年中國人口數量如表3所示.表4為預測均方誤差.表4表明在對中國人口數量進行預測時,非參數貝葉斯估計與局部線性回歸相比較,均方誤差較小,在一定程度上克服了局部線性回歸方法在預測外推方面效果較差的問題.

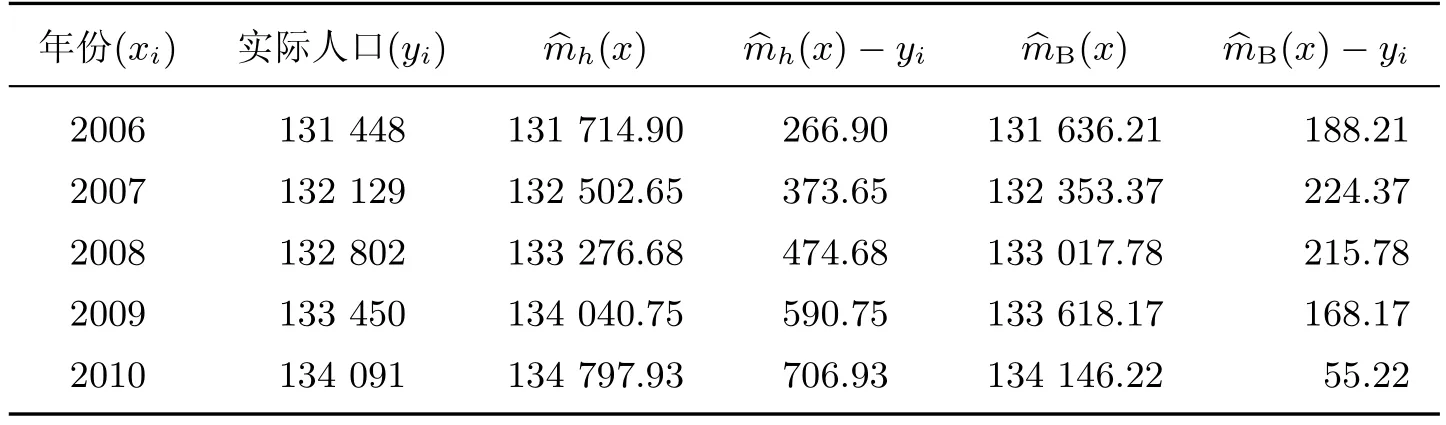
表3 2006—2010年中國人口數量預測結果Table 3 China's population forcast results from 2006 to 2010 萬人

表4 預測均方誤差MSETable 4 Prediction mean square error MSE 萬人

3 結束語

本工作利用Y對X的條件分布的非參數貝葉斯估計來構造回歸函數的非參數貝葉斯估計,在此過程中,用分布估計的核估計替代Ferguson估計的經驗分布函數,用較高階的局部多項式回歸替代原構造中的Nadaraya-Watson回歸估計,獲得了較為理想的估計效果,同時還給出了估計的均方誤差及其均方收斂性.實證結果表明,對于非參數貝葉斯估計,當先驗分布選擇較合適時,在數據擬合和預測方面均表現出了較好的效果.