一種引用全相參技術的連續波相位測距方法

汪瀚文， 張丕狀

(中北大學 信息探測與處理重點實驗室， 山西 太原 030051)

0 引 言

隨著現代化科學技術的日益發展， 在各個應用領域中， 測距儀器的應用范疇越來越廣泛， 對于測距儀測量的要求也越來越高. 為了追求更高的測量范圍和測量精度， 人們不斷地研究新的測距方法和技術[1].

連續波相位測距[2]因測量精度高、 近距離不存在盲區、 測距精度與距離無關等優點， 被廣泛應用于測距技術領域， 是公認的最有發展潛力的絕對距離測量技術. 連續波相位測距中連續波的相位信息能夠反映出所測距離長度， 因此相位信息的準確度將直接影響測距系統的精確度. 因而提高測距精度[3]的關鍵之一在于鑒相技術的改進[4].

發射波的調制信號頻率和數據采集的采樣頻率會影響相位信息， 而信號頻率和采樣頻率都是由晶振提供的， 每一個晶振的頻率都不是完全精確的， 而是存在一定的誤差值， 且不同晶振的誤差值也不盡相同. 晶振頻率的誤差會使得信號頻率和采樣頻率產生相應的誤差， 從而使得測量的相位值產生誤差， 最終影響測距系統的精度.

相參技術早在聲學和光學中就有應用， 之后應用于雷達系統[5]， 其中雷達發射信號頻率、 本振信號頻率和相參基準信號頻率全部由自主震源頻率提供， 從而保持穩定的相位同步關系.

本文旨在提出一種引用雷達“全相參”[6]技術的方法， 通過同一晶振給發射信號和數據采集提供震源， 使信號頻率和采樣頻率的誤差值同步， 從而降低因晶振頻率的誤差產生的測量誤差， 進而提高測量的精確度.

1 向量內積鑒相法原理

內積鑒相法[7]的算法原理是基于一個信號與初始相位為零的信號的相位差， 它是通過傅里葉變化推導出來的， 推導過程為：

按照傅里葉級數的定義[8]， 若三角函數y(t)的周期為T， 角頻率為ω， 其傅里葉級數展開式為

(1)

式中：n為正整數， 各次諧波成分的幅度值為：

直流分量的幅度

(2)

余弦分量的幅度

(3)

正弦分量的幅度

(4)

式中：n=1,2,3,….

若將式(1)中的同頻率項加以合并， 可以寫成另一種形式

(5)

比較式(1)和(5)可以看出傅里葉級數中各個量之間的關系：

a0=c0,

an=cncosφn,

bn=-c0sinφn.

(6)

因此， 由式(6)中的各關系可推出

(7)

則

(8)

由以上推論可得： 對于余弦信號

y(t)=Acos(2πft+φ),

(9)

則其相位差

(10)

式中：

(11)

式中：n為采樣點數；fs為采樣頻率， 則其對應的數字信號的相位差

(12)

2 引用全相參技術的測相方法

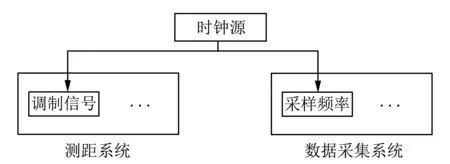
圖 1 引用全相參的測距系統結構圖Fig.1 Reference to the structure of the ranging system of the full coherence

在向量內積鑒相法中[9]， 調制信號的頻率和數據采集的采樣頻率會直接影響鑒相結果. 在實際應用中， 由于提供調制信號頻率的晶振和數據采集中采樣頻率的晶振都不是完全精準的， 導致調制信號的頻率和數據采集的采樣頻率都會存在不同的偏差， 這些偏差都會使得鑒相結果產生不同程度的誤差， 最終影響測距系統的精確性.

在此情況下， 我們在向量內積鑒相法中引用全相參技術[10]， 對于調制信號頻率和數據采集的采樣頻率， 我們全部由同一自主震源頻率提供， 保證了調制信號頻率和采樣頻率誤差的同步性， 如圖 1 所示.

3 理論分析

假設測距系統對距離L的目標物體進行測量.

測距系統的發射信號為

y(t)=A0cos(ωt).

(13)

測距系統的接收回波信號為

y(t)=Acos(ωt+φ).

(14)

數據采集系統以fs的采樣頻率對接收的回波信號進行采樣.

當不引用全相參技術時， 即信號頻率和采樣頻率不來自同一震源頻率， 因此調制信號頻率和采樣頻率的誤差值不同步. 假設調制信號頻率的誤差度為k， 采樣頻率的誤差度為d， 則調制信號頻率為f0+k*f0， 采樣頻率為fs+d*fs.

由式(12)可得相應的相位差

(15)

對式(15)的分子求導可得

(16)

則分子誤差

(17)

同理可得分母誤差

(18)

當引用全相參技術時， 信號頻率和采樣頻率全來自同一震源頻率， 因此調制信號頻率和采樣頻率的誤差值同步. 假設調制信號頻率和采樣頻率的誤差度均為k， 則調制信號頻率為f0+k*f0， 采樣頻率為fs+k*fs.

由式(12)可得相應的相位

(19)

對式(19)的分子求導可得

(20)

則分子誤差

(21)

同理可得分母誤差

(22)

由式(17), (21) 對比和式(18), (22)對比可知， 在全相參條件下的相位差誤差度比在非相參條件下的誤差度更小.

4 仿真分析

試驗中， 測量距離從2～25 m， 每隔0.1 m取一個測量點. 在理想測量條件下， 信號頻率為5 kHz， 采樣頻率為1 MHz. 在實際情況中， 信號頻率和采樣頻率均存在一定誤差值. 假設在全相參條件下， 信號頻率和采樣頻率由同一誤差值為1%的晶振提供； 在非相參條件下， 信號頻率由誤差值為1%的晶振提供， 采樣頻率由誤差值為2%的晶振提供. 通過Matlab仿真后， 分別得到在理想條件、 全相參條件、 非相參條下測量距離和信號相位的關系曲線(見圖 2)和全相參條件、 非相參條件下測量距離和相位誤差度的關系曲線(見圖 3).

由圖2測量距離和信號相位差的曲線圖可知： 在全相參條件下測得的回波信號和發射信號的相位差與在非相參條件下測得的回波信號和發射信號的相位差進行對比， 全相參條件下回波信號和發射信號的相位差更接近理想情況下回波信號和發射信號的相位差.

由圖3測量距離和相位誤差度的曲線圖可知： 在全相參條件下測得的回波信號和發射信號的相位差的誤差度要比在非相參條件下測得的回波信號和發射信號的相位差的誤差度要更小， 因此在全相參條件下測距系統的精確度更高.

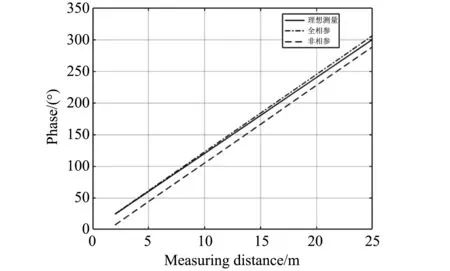
圖 2 測量距離和信號相位的曲線圖Fig.2 Measuring distance and signal phase

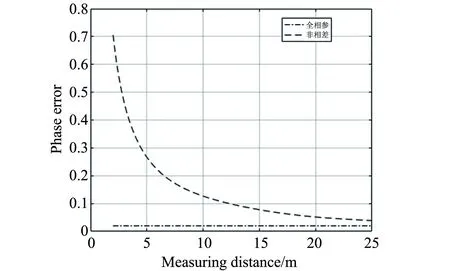
圖 3 測量距離和相位誤差的曲線圖Fig.3 Measuring the distance and phase error

5 結 論

本文在提高測距精確度的背景下， 提出一種引用全相參技術的連續波相位測距方法， 通過理論分析和仿真驗證， 證實了該方法能有效提高測距系統的精確度， 具有一定的應用價值.